Introduction

Since a two-dimensional topological insulator phase, also known as a quantum spin Hall state, was predicted in graphene with sizable spin-orbit coupling (SOC)1,2, there has been tremendous interest in the exploration of topological materials, including topological insulators (TIs) and topological semimetals (TSMs), due to their unusual physical phenomena and potential applications3,4,5,6,7,8,9. One of the intriguing characteristics of TIs is the presence of a bulk insulating gap as well as gapless boundary states that form a Dirac point4,5,10,11,12. In contrast, TSMs are characterized by gapless bulk states and Fermi arc surface states6,7,8,9. In TSMs, the band crossing near the Fermi level occurs at discrete points (Dirac and Weyl semimetals) or along curves (nodal line semimetals) in reciprocal space. The band crossing points created by band overlap are protected by topology and symmetry9,13.

In TIs characterized by a \({\Bbb Z}_2\) topological invariant, the gapless edge or surface states across the band gap are topologically protected from scattering by time-reversal symmetry (TRS)1,14. The metallic boundary states of \({\Bbb Z}_2\) TIs host a unique helical spin texture and allow dissipationless spin-filtered charge transport in potential applications for quantum computing and spintronic devices15,16. Since bulk band splitting created by SOC is usually small, limiting practical applications at room temperature, it is desirable to explore TIs with large band gaps and boundary states within the band gap17,18,19,20,21,22,23. In contrast, in topological crystalline insulators (TCIs), crystal symmetries such as mirror reflection symmetry play a key role in the topological nature of electronic states24. The TCI phase can be characterized by topological invariants related to crystal symmetry. The most well-known invariant is the mirror Chern number \(C_{\Bbb M}\) for mirror symmetry25. Similar to TRS-protected TIs, TCIs possess gapless surface states across the insulating bulk gap. The TCI phase was theoretically predicted and experimentally realized in SnTe26,27, Pb1-xSnxSe28, and Pb1-xSnxTe29.

Recently, a new class of TIs called dual topological insulators (DTIs) have been reported, in which \({\Bbb Z}_2\) TI and TCI phases coexist25,30,31,32,33,34,35,36. The DTI phase, characterized by both \({\Bbb Z}_2\) indices and TCI topological invariants, also has gapless surface states protected against perturbations that individually break TRS or mirror symmetry. The advantage of the dual topological characteristic is that more stable DTI-based devices can be designed. The DTI phase has been theoretically proposed for several materials, such as Bi1-xSbx25, Bi2Te330, Na3Bi31, Pt2HgSe334, Na2MgPb35, and Na2CdSn35, and experimentally verified for Bi1Te132, Bi0.91Sb0.0933, and Pt2HgSe336.

In this work, we theoretically propose that NaZnBi in a tetragonal structure belongs to a class of DTIs with both time-reversal and mirror symmetries. First-principles calculations show that NaZnBi is a strong topological insulator (STI) with \({\Bbb Z}_2\) topological indices \((\nu _0;\nu _1\nu _2\nu _3) = (1;000)\) and that the TCI character is well identified by the odd mirror Chern numbers \(C_{{{\mathrm{M}}}} = - 1\) and +1 for the (100) and \((1\bar 10)\) mirror invariant planes, respectively. The surface states form a Dirac cone at a time-reversal invariant momentum (TRIM), consistent with the calculated topological invariants and mirror Chern numbers. The Dirac cone made by gapless surface states is robust against perturbations that break either the TRS or mirror symmetry unless both symmetries are simultaneously broken.

Methods

First-principles electronic structure calculations were performed within the density functional theory framework. We used the generalized gradient approximation (GGA) of Perdew-Burke-Ernzerhof (PBE) for the exchange-correlation functional37 and the projector augmented wave potentials, as implemented in the VASP code38. The wave functions were expanded in plane waves up to an energy cutoff of 600 eV, and a set of 12 × 12 × 8 Γ-centered k-points was used for Brillouin zone (BZ) integration. The atomic coordinates were fully optimized until the residual forces were less than 0.1 meV/Å.

For Wannier charge center calculations, we obtained maximally localized Wannier functions using the WANNIER90 code39. Green’s function method40 was used to calculate the surface electronic spectrum, as implemented in the WannierTools code41. To calculate the mirror Chern numbers, we selected twelve valence bands close to the Fermi level, which were obtained by employing norm-conserving Vanderbilt pseudopotentials, as implemented in the Quantum ESPRESSO42 and Z2Pack codes43. In this case, we chose the kinetic energy cutoff of 50 Ry for wave functions expanded in plane waves and the 12 × 12 × 8 k-point mesh for BZ integration.

We explored the low-energy crystal structures of NaZnBi by using an ab initio evolutionary crystal structure search method, as implemented in the AMADEUS code44. Distinct configurations were generated for supercells containing 2 and 4 formula units by employing the conformational space annealing algorithm for global optimization. The k-point mesh with a grid spacing of 2π × 0.25 Å−1 and a kinetic energy cutoff of 400 eV were adopted.

To examine the Zeeman effect on the dual topological character of NaZnBi, we added the following Zeeman coupling to the tight-binding model Hamiltonian built by using the maximally localized Wannier functions, \(H_{{{\mathrm{Z}}}} = \mu _{{{\mathrm{B}}}}g_J\mathop{B}\limits^{\rightharpoonup} \cdot \mathop{J}\limits^{\rightharpoonup}\), where μB, \(\mathop{B}\limits^{\rightharpoonup}\), and \(\mathop{J}\limits^{\rightharpoonup}\) are the Bohr magneton, external magnetic field, and total angular momentum, respectively. In addition, the Landé g-factor gJ is given by \(g_J = \frac{3}{2} + \frac{{S\left( {S + 1} \right) - L\left( {L + 1} \right)}}{{2J\left( {J + 1} \right)}}\), where L and S are the quantum numbers of the orbital and spin angular momenta, respectively.

Results

Crystal symmetry of NaZnBi

Zintl AZnX (A = Li, Na, K; X = P, As, Sb, Bi) compounds have been synthesized and have drawn considerable interest because of their potential applications in photovoltaics, thermoelectrics, and Li-ion batteries45,46,47,48,49. The crystal structure of these AZnX compounds is highly dependent on the type of cation A. Li-based compounds crystallize in a cubic structure with the space group \(F\bar 43m\) for X = P and As, whereas these compounds crystallize in a hexagonal structure with the space group P63 mc for X = Sb and Bi50,51,52. Alternatively, the Na- and K-based compounds crystallize in tetragonal P4/nmm and hexagonal P63/mmc structures, respectively, regardless of the type of anion X53,54,55,56,57,58 (see Supplementary Fig. S1). Very recently, a single crystal of NaZnBi with P4/nmm symmetry was synthesized57. To investigate the stable phase of NaZnBi, we performed ab initio evolutionary crystal structure search calculations, as implemented in the AMADEUS code44, and confirmed that the tetragonal P4/nmm structure is most stable (see Supplementary Fig. S2), with energies lower by 1.5 and 90.9 meV/f.u., compared to the P63 mc and P63/mmc structures, respectively. The calculated lattice parameters of P4/nmm-NaZnBi are a = b = 4.6585 Å and c = 7.5257 Å, in good agreement with the experimentally measured values of a = b = 4.5114 Å and c = 7.5970 Å57 (see details in Supplementary Table S1).

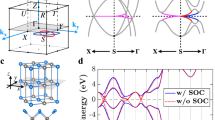
The tetragonal P4/nmm lattice of NaZnBi is composed of ZnBi layers and embedded Na atoms. In each ZnBi layer, the Zn atoms form a planar square lattice and are tetrahedrally bonded with the Bi atoms arranged in staggered rows above and below the Zn layer (Fig. 1a and Supplementary Fig. S3). The Na atoms are intercalated also in staggered rows between ZnBi layers and are surrounded by the Bi atoms forming a square pyramid. This P4/nmm lattice is characterized by four important symmetries (Fig. 1b): a fourfold \({\Bbb C}_{4z}\) rotation about the z-axis, a glide reflection \(\tilde {\Bbb M}_{(001)}\) with the (001) mirror reflection, followed by a half-translation along the [110] direction, and two mirror reflections with respect to the (100) and \((1\bar 10)\) planes, which are denoted as \({\Bbb M}_{(100)}\) and \({\Bbb M}_{(1\bar 10)}\), respectively. In addition, the crystal structure of NaZnBi has inversion symmetry. With TRS, each band has twofold degeneracy at any k-point in the BZ (Fig. 1c). Focusing on the four mirror planes in Fig. 1b, the mirror symmetry \({\Bbb M}_{(100)}\) has two invariant planes with kx = 0 and kx = π [henceforth, (kx, ky, kz) is given in units of (1/a, 1/b, 1/c)]. For the mirror symmetry \({\Bbb M}_{(1\bar 10)}\), the kx = ky plane is invariant. Therefore, when the bulk BZ is projected onto the (001) surface, the k-paths of \(\overline {\overline {\mathrm{\Gamma}}} - \overline {\overline X}\) and \(\overline {\overline {\mathrm{\Gamma}}} - \overline {\overline M}\) become invariant lines under \({\Bbb M}_{(100)}\) and \({\Bbb M}_{(1\bar 10)}\), respectively. On the (100) surface BZ, the path between \(\overline {\mathrm{\Gamma}}\) and \(\overline Z\) is invariant under \({\Bbb M}_{(010)}\).

Fig. 1: Atomic structure and crystal symmetry in NaZnBi.
figure 1

a Crystal structure of NaZnBi in the tetragonal P4/nmm lattice, which is composed of ZnBi layers and embedded Na atoms. b Top and side views of the atomic structure of NaZnBi. Dashed lines represent the mirror planes for four mirror reflection symmetries, \({\Bbb M}_{(100)}\), \({\Bbb M}_{(010)}\), \({\Bbb M}_{(110)}\), and \({\Bbb M}_{(1\bar 10)}\). c In bulk and two-dimensional surface BZs, TRIM points and their projection onto the (100) and (001) surfaces are indicated.

Full size image

Electronic structure and band inversion

In previous theoretical calculations where a modified Becke–Johnson potential (mBJ) was used for the exchange-correlation potential, NaZnP, NaZnAs, and NaZnSb were shown to be semiconductors with direct band gaps of 1.80, 1.47, and 0.25 eV, respectively47. A clear trend is observed in which the band gap decreases as the anionic radius increases from P to Sb. Notably, while a recent experiment reported a narrow semiconducting gap for NaZnSb59, previous generalized gradient approximation (GGA) and local density approximation (LDA) calculations60,61 generated a metallic band structure for NaZnSb. In the current study, we mainly present the results of GGA and double-check our conclusions with a hybrid functional.

Our calculation shows that bulk NaZnBi is metallic in the absence of SOC with a severe band overlap between the valence and conduction bands (Fig. 2a). By including SOC, on the other hand, the valence and conduction bands are well separated, creating a spin-orbit gap in the whole BZ (Fig. 2b). This result likely indicates that the electronic states may be topologically nontrivial. For the band gap, NaZnBi exhibits semimetallic behavior with the valence band maximum (lying in the M - Γ line) above the Fermi level and the conduction band minimum (along the Z-R line) below the Fermi level. This semimetallic behavior is maintained in a trilayered-NaZnBi thin film, Cd-alloyed Na(Zn0.9Cd0.1)Bi, and strained-NaZnBi under 3% biaxial tensile strain. Our results of the HSE06 hybrid functional62 also show that the semimetallic behavior is still maintained regardless of the SOC (see Supplementary Fig. S4).

Fig. 2: Band structure of NaZnBi.
figure 2

The bulk band structures of NaZnBi in the tetragonal P4/nmm lattice, which are calculated a without and b with including the spin-orbit coupling. The Fermi level is set to zero.

Full size image

NaZnBi as a strong topological insulator

To investigate the \({\Bbb Z}_2\) band topology and nontrivial surface states, we performed Wannier charge center (WCC) calculations on six TRIM planes with ki = 0 and π (i = x, y, z). Figure 3a shows the flow of the WCCs along one of the k paths on these six invariant planes. On the ki = 0 planes (i = x, y, z), the WCCs exhibit an odd number of crossings with any horizontal line chosen as a reference line in the half BZ. On the other invariant planes with ki = π (i = x, y, z), we found an even number of crossings. These results indicate that the three planes with ki = 0 (i = x, y, z) are topologically nontrivial with the invariant \({\Bbb Z}_2 = 1\), whereas the other three with ki = π (i = x, y, z) are trivial as \({\Bbb Z}_2 = 0\). Four independent 3D topological invariants are now determined \((\nu _0;\nu _1\nu _2\nu _3) = (1;000)\), implying that bulk NaZnBi is a STI protected by TRS. This conclusion can be double-checked by calculating the product of parity eigenvalues (δ) for the occupied bands. The δ values at TRIM points are found to be δ = +1 at Γ and δ = −1 at all the other seven points, consistent with the \({\Bbb Z}_2\) invariant obtained from the WCCs. For the case of NaZnSb, on the other hand, we found it is a trivial insulator due to a weak SOC.

Fig. 3: Flow of Wannier charge centers.
figure 3

a The flow of WCCs is plotted for six TRIM planes with ki = 0 and π (i = x, y, z). With odd numbers of crossings in the half BZ, NaZnBi is classified as a strong topological insulator with topological invariants \((\nu _0;\nu _1\nu _2\nu _3) = (1;000)\). b For twelve valence bands close to the Fermi level, the flow of WCCs is plotted for the kx = 0 (top) and kx = ky (bottom) planes invariant under \({\Bbb M}_{(100)}\) and \({\Bbb M}_{(1\bar 10)}\), respectively. The mirror eigensector with the eigenvalue +i (−i) is shown in the left (right) panel, and red dots represent the summation of WCCs for each eigensector. As the basis vectors (a, b, c) change from (1,0,0), (0,1,0), and (0,0,1) to (1,1,0), (1,−1,0), and (0,0,1), respectively, where a, b, and c are the coefficients of primitive translation vectors, a′ represents the coefficient of the (1,1,0) vector.

Full size image

NaZnBi as a DTI

The presence of the four mirror symmetries suggests an intriguing possibility that NaZnBi can also be a TCI. To examine the mirror Chern number, we focused on two particular mirror symmetry operations \({\Bbb M}_{(100)}\) and \({\Bbb M}_{(1\bar 10)}\) because other operations \({\Bbb M}_{(010)}\) and \({\Bbb M}_{(110)}\) are basically equivalent to \({\Bbb M}_{(100)}\) and \({\Bbb M}_{(1\bar 10)}\), respectively, followed by the fourfold \({\Bbb C}_{4z}\) rotation about the z-axis. Our calculations were performed by considering twelve valence bands near the Fermi level. Figure 3b shows the flow of WCCs in two mirror eigensectors ±i on the kx = 0 and kx = ky planes, which are invariant under \({\Bbb M}_{(100)}\) and \({\Bbb M}_{(1\bar 10)}\), respectively. The red dots show the calculated WCCs whose sum yields the winding and Chern number for the given eigensectors. From WCC flow, the Chern number C±i is found to be ∓1 for the \({\Bbb M}_{(100)}\) eigensector ±i, and it gives rise to the mirror Chern number \(C_{\Bbb M} = \frac{{C_{ + i} - C_{ - i}}}{2} = - 1\) on the kx = 0 plane. Similarly, for \({\Bbb M}_{(1\bar 10)}\), \(C_{\Bbb M} = + 1\) on the \((1\bar 10)\) plane. From the nonzero mirror Chern numbers for both \({\Bbb M}_{(100)}\) and \({\Bbb M}_{(1\bar 10)}\), NaZnBi is classified as a TCI. Combined with the nonzero \({\Bbb Z}_2\) indices, NaZnBi is hereby suggested as a DTI.

Surface electronic structure

The DTI nature of NaZnBi can also be seen in the surface electronic structure. Figure 4a and b present our calculation results on the (100) and (001) surfaces, respectively, which show the topological band crossings at the \(\overline {\mathrm{\Gamma}}\) and \(\overline {\overline {\mathrm{\Gamma}}}\) points accompanied by the Kramers partner exchange. This result is in good agreement with the abovementioned \((\nu _0;\nu _1\nu _2\nu _3) = (1;000)\). In the sense that the topological band crossing is located at \(\overline {\mathrm{\Gamma}}\), the result of the (100) surface is also consistent with \(C_{\Bbb M} = - 1\) for \({\Bbb M}_{(010)}\). On the other hand, the topological features are not quite clear in the (001) surface bands shown in Fig. 4b. This is largely because the detailed characteristics of the two band crossings in \(\overline {\overline M} - \overline {\overline {\mathrm{\Gamma}}}\) and \(\overline {\overline {\mathrm{\Gamma}}} - \overline {\overline X}\) (highlighted by black square boxes) are not obvious. In the discussion below, however, it will become clear that the topological surface Dirac point occurs at \(\overline {\overline {\mathrm{\Gamma}}}\) as required by the calculated \({\Bbb Z}_2\) indices. Although the surface bands near \(\overline {\overline {\mathrm{\Gamma}}}\) are buried in the bulk bands, we found that the \(\overline {\overline {\mathrm{\Gamma}}}\) crossing is the one between two bands that connect the bulk valence and conduction bands, which is therefore consistent with the results of \(C_{\Bbb M} = - 1/\! +\! 1\) for \({\Bbb M}_{(100)/(1\bar 10)}\). The band crossings in the symmetry lines \(\overline Z - \overline {\mathrm{\Gamma}}\) and \(\overline {\overline {\mathrm{\Gamma}}} - \overline {\overline X}\) are attributed to \({\Bbb M}_{(010)}\) and \({\Bbb M}_{(100)}\) symmetries, respectively, and are destroyed by increasing SOC strength (see Supplementary Fig. S5).

Fig. 4: Surface electronic structure.
figure 4

The surface electronic structure projected onto the a (100) and b (001) surfaces is plotted along the high symmetry lines shown in Fig. 1c. The thickness of the colored lines represents the degree of contribution by surface electronic states. The Green function approach is used for the tight-binding model Hamiltonian built in terms of maximally localized Wannier functions. In b, the surface band crossings at the \(\overline {\overline {\mathrm{\Gamma}}}\) point and on the \(\overline {\overline M} - \overline {\overline {\mathrm{\Gamma}}}\) and \(\overline {\overline {\mathrm{\Gamma}}} - \overline {\overline X}\) lines are enlarged inside insets.

Full size image

Surface band crossings and dual protections

Protected by both TRS and crystalline symmetry, the topological surface band in a DTI is quite robust. To see its response to symmetry-breaking perturbations, we investigated the surface band structure under the Zeeman field, which breaks the TRS. The effect of the magnetic field is taken into account within the tight-binding model Hamiltonian obtained from maximally localized Wannier functions (see the Methods section for the details of computations). Note that while TRS is completely broken by the field, the mirror symmetries are only partly broken depending on its directions; namely, the mirror reflection whose mirror plane is normal to the field is preserved.

Figure 5a–c show the band structures projected onto the (100) surface under the external magnetic field along the x-, y-, and z-axes, respectively. As the mirror plane is perpendicular to this surface (see Fig. 1b), \({\Bbb M}_{(010)}\) is the only mirror symmetry remaining on this surface. It is clearly noted that the topological surface Dirac point at \(\overline {\mathrm{\Gamma}}\) is preserved when the magnetic field is along the y-axis, namely, perpendicular to the \({\Bbb M}_{(010)}\) symmetry plane (Fig. 5b), even though its position is slightly shifted toward +\(\overline {\mathrm{Z}}\). This is because the \({\Bbb M}_{(010)}\) mirror symmetry is maintained despite the broken TRS. Thus, this phase is no longer an STI but still a TCI. On the other hand, the fields along the x and z directions break the \({\Bbb M}_{(010)}\) symmetry as well as the TRS and therefore induce a topological phase transition from a DTI to a trivial insulator with finite band gaps of approximately 60 and 40 meV at the Dirac point, as shown in Fig. 5a and c, respectively.

Fig. 5: (100) Surface electronic structure with symmetry-breaking perturbation.
figure 5

The (100) surface electronic structure of NaZnBi when a magnetic field (μB B = 0.05 eV) is applied in the (a) x, (b) y, and (c) z directions. In b, only if the magnetic field is applied in the y direction that is normal to the \({\Bbb M}_{(010)}\) symmetry plane is the Dirac cone at \(\overline {\mathrm{\Gamma}}\) preserved with a slight shift toward the \(\overline Z\) point. d When the lattice is additionally distorted by shifting one Bi site in a unit cell by 0.1 Å in the y direction, with the magnetic field (μB B = 0.05 eV) applied in the y direction, the \({\Bbb M}_{(010)}\) symmetry is broken, and the band degeneracy at the Dirac cone is lifted.

Full size image

As expected, the band crossing protected by \({\Bbb M}_{(010)}\) symmetry even under the field along the y direction (Fig. 5b) is eventually destroyed by atomic movements that break the mirror symmetry. In Fig. 5d, band splitting of approximately 10 meV is clearly observed at the Dirac point, with the Bi position slightly shifted by 0.1 Å along the y direction. This result supports our conclusion and interpretation regarding the DTI and its surface band characteristics.

We performed the same analyses on the (001) surface. Figure 6a shows the calculated band structure obtained by shifting one Bi atom by 0.1 Å along the y direction without the Zeeman field. Due to the presence of \({\Bbb M}_{(100)}\) symmetry as well as TRS, the Dirac point at \(\overline {\overline {\Gamma}}\) is well maintained. Along the \(\overline {\overline M} - \overline {\overline {\Gamma}}\) line, on the other hand, there is no band crossing, which is attributed to the broken \({\Bbb M}_{(1\bar 10)}\) symmetry by the atomic displacement of Bi. Now, we destroy the \({\Bbb M}_{(100)}\) symmetry by shifting the position of Bi along the [110] direction. Figure 6c shows that, as expected, the crossing point previously observed in the \(\overline {\overline {\Gamma}} - \overline {\overline X}\) line disappears. Finally, we take into account the magnetic field. Due to the dual nature, the \(\overline {\overline {\Gamma}}\) crossing survives even under the broken TRS as far as the field direction is normal to the mirror operation plane. Figure 6b and d clearly show that the fields in the [100] and \([1\bar 10]\) directions do not destroy the Dirac points along the \(\overline {\overline {\Gamma}} - \pm \overline {\overline X}\) and \(\overline {\overline {\Gamma}} - \pm \overline {\overline M} /4\) lines, respectively. These analyses provide further evidence that NaZnBi is a DTI whose topological surface Dirac crossing is protected by both time-reversal and mirror symmetries and therefore are robust against the breaking of any one of those.

Fig. 6: (001) Surface electronic structure with symmetry-breaking perturbation.
figure 6

a, b The (001) surface electronic structure of NaZnBi for a distorted lattice, in which one Bi site in a unit cell is shifted by 0.1 Å in the y direction while preserving the \({\Bbb M}_{(100)}\) symmetry. c, d In another distorted lattice, one Bi site in a unit cell is shifted by 0.1 Å in the [110] direction; thus, the \({\Bbb M}_{(1\bar 10)}\) symmetry is maintained. In a and c, there is no external magnetic field, whereas in b, d, an additional magnetic field (μB B = 0.05 eV) is applied in the [100] and \([1\bar 10]\) directions, respectively, breaking the TRS.

Full size image

In conclusion, we clearly show the nontrivial topological characteristic in recently synthesized NaZnBi57. Due to the large bandwidth and the strong SOC of the Bi atom, NaZnBi is a DTI, while NaZnX (X = P, As, and Sb) are trivial insulators. As an STI, any surface of NaZnBi can host the topological Dirac crossing. In experiments such as angle-resolved photoemission, it is desirable to investigate the (100) surface on which the characteristic crossing is clearly seen, as illustrated in Fig. 4. Another interesting future direction is the study of pressure. We found a topological phase transition from the DTI phase to the TCI phase by applying hydrostatic pressure, which reduces the band splitting at Γ. As a result, the band inversion disappears at an approximately 18% volume compression (see Supplementary Fig. S6), and the TCI phase appears at higher pressure, with Chern numbers CM = −2 and 0 for \({\Bbb M}_{(100)}\) and \({\Bbb M}_{(1\bar 10)}\), respectively. Our study can hopefully stimulate the experimental verification and further exploration of topological phases in this recently synthesized material.