Abstract
Interface-related phenomena have great potential to control the superconducting state in Fe-based superconductors. We propose a comprehensive classification of Fe-pnictide heterointerfaces based on electrostatic principles that allow the prediction of the interface microstructure, in particular, distinguishing between clean heterointerfaces and the formation of interfacial layers. The concept was successfully tested on a novel LnOFeAs/BaFe2As2 (Ln = La, Sm) Fe-pnictide heterostructure. With the addition of different cations/anions, it is possible to produce clean interfaces or interfacial layers. The impact of the microstructure on superconductivity in the Fe-pnictide heterostructures is discussed.
Similar content being viewed by others
Introduction
The design and study of functional interfaces has become increasingly important in the interdisciplinary fields of materials science, condensed matter, and applied physics. In the context of Fe-based superconductors, the controlled engineering of novel interfaces is starting to play a key role. On the one hand, it helps to elucidate the interplay between charge, spin, and lattice degrees of freedom that might be relevant for high-temperature superconductivity; on the other hand, it is required to advance the potential for device applications. Recently, the heterointerface between a Fe-chalcogenide and a perovskite oxide in monolayer (ML-) FeSe/SrTiO3 demonstrated an ability to host high-temperature superconductivity in the range of 40–75 K.1,2,3 This transition temperature, which exceeds the value of its bulk counterpart by almost one order of magnitude, is believed to be the result of a cooperative (interfacial) Cooper pairing interaction.4
While interface engineering of ML-FeSe/SrTiO3 has attracted much attention and established protocols have been worked out,5 analogous interfacial control for Fe-pnictide superconductors is less developed because generalized engineering concepts are lacking. In contrast to the van der Waals compound FeSe,5 Fe-pnictides are polar layered compounds, which is of great relevance for their surface and interface properties. In many cases, Fe-pnictide heterointerfaces are found with an additional reaction layer that complicates interfacial superconductivity or junction design. Nevertheless, we show that interface-related phenomena in Fe-based superconductors hold exceptional promise for their further design and exploration once their microstructure is understood in detail.
The here proposed comprehensive classification of Fe-pnictide heterointerfaces makes effective use of the polar layered structure of Fe-pnictides and emphasizes that electrostatic principles govern the interfacial microstructure and interface design. According to this classification, the formation of an additional interfacial layer can be easily understood and predicted. Furthermore, we successfully tested the concept within a series of LnOFeAs/BaFe2As2 (Ln = La, Sm) Fe-pnictide heterostructures. We believe that the concept can be generalized to other polar layered compounds.
Materials and methods
LnOFeAs/BaFe2As2 thin film heterostructures with Ln = La, Sm (“Ln-1111/Ba-122”) were grown by pulsed laser deposition (PLD) using a Spectra-Physics Quanta Ray INDI Nd:YAG(2ω) laser (λ = 532 nm, 10 Hz, τ < 10 ns) in an ultrahigh vacuum (UHV) chamber (pbase = 10–9–10–8 mbar). Targets of BaFe2As2, LnOFe0.85Co0.15As, and SmO1-xFeAs with x ~0 and 0.1 (ε ≈ 2–3 J cm–2) were employed and resulted in LnOFe1-xCoxAs/Ba(Fe1-xCox)2As2, LnOFeAs/BaFe2As2, and LnOFeAs/IFL/BaFe2As2 with an interface layer (IFL). The Co2+ and O2– supply was controlled by the Ln-1111 target composition. Due to As loss in the deposition process, we talk about an O-excess in the case of the almost stoichiometric target in comparison to the O-deficient target. All films were deposited on MgO(100) substrates that were preheat-treated in the air at 800 °C for 1–3 h before they were inserted into the UHV environment. The substrate temperature (~850 °C) was held constant during the deposition of both Fe-pnictide layers. Further details of film growth and target preparation are given in the SI (Table S1 and Figs. S1, S2) and in refs. 6,7
Structural characterization was performed with X-ray diffraction (XRD) (Rigaku Smart Lab, Cu Kα, Bragg-Brentano, tube current of 200 mA, and voltage of 45 kV). The c-axis lattice parameters were calculated from the (00 l) reflections using the extrapolation function, f(θ) = [cos(θ)cot(θ) + 1/θ]. Layer thicknesses were acquired from X-ray reflectivity (XRR) measurements (cross-beam optics unit, Ge(220) monochromator). Analysis was performed with Global Fit software.
Auger electron spectroscopy (AES) was carried out on an ULVAC-Phi 710 Auger electron spectrometer integrated into a scanning electron microscope (SEM) with a primary electron beam of 10 kV. An incident electron current of 10 nA on scanned areas between 9 µm2 and 150 µm in diameter resulted in current densities between 57 µA cm–2 and 111 mA cm–2 on the film surfaces. For analysis, clean areas without droplets were chosen. AES depth profiles were obtained by Ar+ ion sputtering (1 kV on an area of 2 mm2 × 2 mm2). To decrease the effectively sputtered film area to ~0.78 mm2, the film surfaces were covered by an Al foil having a hole of ~1 mm in diameter. Auger spectra, N(E), were recorded in the range of E = 30–1500 eV with a step size ΔE = 1 eV (Table S2 and Figs. S3, S4). The data were processed using Phi MultiPak software. The quantitative analysis of the element concentrations in the heterostructures was based on relative sensitivity factors using the peak-to-peak heights of the differentiated spectra E·dN/dE (S5D5).
Analytical and scanning transmission electron microscopy (STEM) were carried out for three different heterostructures. A specimen from a LaOFe1-xCoxAs/Ba(Fe1-xCox)2As2 heterostructure was thinned to electron transparency by ion milling at Tokyo Institute of Technology, where STEM was carried out on a JEOL JEM ARM200F microscope (JEOL Ltd., Akishima, Japan) with a probe spherical aberration corrector operated at an accelerating voltage of 200 kV. The high-angle annular dark-field (HAADF) imaging conditions included a probe size of 0.1 nm, a semiconvergence angle of 32 mrad, and an annular detection angle of 80–170 mrad. Electron energy loss spectroscopy (EELS) was performed using a Gatan Enfina spectrometer (collection semiangle of 12.5 mrad). The spectra were recorded with a dispersion of ΔE = 0.1 eV/channel (Table S3 and Fig. S5).
Two comparable heterostructures of LaOFe1-xCoxAs/Ba(Fe1-xCox)2As2 and SmOFe1-xCoxAs/Ba(Fe1-xCox)2As2 were analyzed by HAADF-STEM at the University of Glasgow. The TEM lamellae were prepared by a standard focused ion beam (FIB) lift-out technique performed using a Xenon Plasma FIB instrument, which allowed the extraction of longer cross-sections with less Ga implantation or surface damage than with a conventional Ga beam FIB.8 STEM imaging and analysis were performed using a JEOL JEM ARM200F (scanning) transmission electron microscope equipped with a probe aberration corrector operated at 200 kV. HAADF-STEM imaging and EDS were performed using a probe convergence angle of 29 mrad. The HAADF-STEM imaging employed an inner collection angle of ~100 mrad. EDS analysis was performed using a Bruker 60 mm2 SDD EDS spectrometer (Bruker Nano GmbH, Berlin, Germany), and the acquisition was controlled by spectrum imaging within a Gatan Digital Micrograph (Gatan Inc., Pleasanton, CA, USA). To obtain sufficient signal-to-noise for robust and reliable detection and quantification of the results without using long dwell times per pixel and risking beam damage, the same box was scanned multiple times, with cross-correlation after each scan to correct for any drift of the sample. Quantification of these results was performed using the Elemental Analysis plugin for Gatan Digital Micrograph. Scanning precession electron diffraction (SPED) was performed in transmission electron microscopy mode using the smallest condenser aperture available (10 µm) to obtain a low convergence angle together with very small spot size. The precession and scanning of the beam were controlled by a NanoMEGAS DigiSTAR system (NanoMEGAS SPRL, Brussels, Belgium) with the scan areas and acquisition handled by their Topspin software. In this case, the diffraction patterns were acquired using a prototype system with a Merlin for an EM direct electron detector (Quantum Detectors Ltd., Harwell, UK) instead of the normal CCD camera pointed at the focusing screen,9 as recently benchmarked and more fully described in ref. 10 Virtual dark field (VDF) imaging of the different phases was then accomplished using the method described in ref. 11 where the data files were read into Python and processed using the fpd Python library (https://fpdpy.gitlab.io/fpd/fpd.html) to numerically integrate the intensity in each diffraction pattern within different periodic arrays of apertures set to correspond to the diffraction spots unique to each of the crystalline phases (and to avoid diffraction spots common to more than one phase).
Electrical transport measurements (four probe) were carried out in a Quantum Design Physical Property Measurement System (PPMS) equipped with a sample rotator stage in external magnetic fields up to µ0H = 9 T and down to 2 K. A constant current of 1 µA was used in all R(T) and R(H;θ) measurements. For the electrical contacts, Cu wires (diameter of 0.01 mm) were attached to the thin film surface using commercial silver paste. Critical temperatures and upper critical fields, µ0Hc2(T;θ), were evaluated using a resistivity criterion (90 to 50% Rn).
Electronic structure calculations were performed within density functional theory and generalized gradient approximation12 for the exchange-correlation functional in the projector-augmented plane wave (PAW) formalism13 as implemented in the Vienna Ab initio Simulation Package (VASP).14 The energy cutoff was set to 500 eV, and the convergence criterion for the electronic density was set to 10–8 eV. For bulk BaFe2As2 and LaFeAsO, we used experimental structures with the tetragonal I4/mmm and P4/nmm space groups, respectively, as reported in ref. 15 The La-1111/Ba-122 heterostructure used in the calculations was constructed by stacking [001]-oriented supercells with four Fe2As2 layers of BaFe2As2 and five Fe2As2 layers of LaFeAsO along the [001] axis with Ba-As termination at the interface and a vacuum space region of 20 Å (SI, Fig. S6). The resulting heterostructure was optimized with the force convergence criterion of 10–3 eV/Å. The Brillouin zone was sampled by a 12 × 12 × 6 mesh for the bulk BaFe2As2, a 12 × 12 × 4 mesh for the bulk LaFeAsO, and a 10 × 10 × 1 mesh for the heterostructure.16 The calculated band structures showing the partial contributions of the Fe d states for the bulk systems and the layer-resolved contributions of the Fe d states for the heterostructure are presented in SI, Fig. S6. The local potential calculated across the heterostructure is shown in the SI Fig. S7 and includes the electrostatic and exchange-correlation potential contributions. The electrostatic potential defined as the sum of the Hartree and ionic potentials shows similar features.
Electrostatic principles explaining the variety of Fe-pnictide heterointerfaces
To date, Fe-pnictides have been grown on various substrates or templates, and the observed heterointerfaces were typically described with an additional reaction layer.17 For a few Fe-pnictide heterostructures, such as Ba(Fe1-xCox)2As2/Fe,18,19 BaFe2As2/SrTiO3,20,21,22,23 and Ba(Fe1-xCox)2As2/BaFe2As2:O,24,25 a coherent atomic arrangement was observed or anticipated. Previous studies have mainly emphasized geometric design plans. Here, we conclude that Fe-pnictide heterointerfaces can be generalized by electrostatic considerations.
Fe-pnictides are polar layered compounds with an alternating layer charge of ±2 and a nonvanishing electric dipole moment. Following the widely accepted typology of nonpolar and polar surfaces and interfaces, which has been successfully used in the description of heterointerfaces such as Ge/GaAs and LaAlO3/SrTiO3,26,27,28,29,30 the assessment of heterointerfaces with Fe-pnictides is summarized in Fig. 1.
The structural unit of the [Fe2As2] layers has a net charge of QL = −2 and a dipole moment, µL ≠ 0. Examples of originally compensated interfaces include a Ba(Fe1-xCox)2As2/Fe, b Ba(Fe1-xCox)2As2/BaFe2As2 (hypothetical), and c LnOFeAs/BaFe2As2 (this work). Here, the interface is within the Fe plane (black arrow). Examples of originally uncompensated interfaces that develop an interfacial layer include Ba(Fe1-xCox)2As2/SrTiO3 d with TiO2 termination and e with SrO termination, f Ba(Fe1-xCox)2As2/(La,Sr)(Al,Ta)O3, and g Ba(Fe1-xCox)2As2/MgO. Compensation is achieved by the valence change within the interfacial layer or by developing a metallic interfacial layer.
The distinct types of interfaces can be classified into originally compensated interfaces, which can be found between Fe-pnictides and metals or Fe-pnictides and polar layers (Fig. 1a–c), and originally uncompensated interfaces (Fig. 1d–g). An originally compensated interface was reported previously for BaFe2As2/Fe (Fig. 1a). Here, we predict and show that the interfaces are compensated and clean after two polar Fe-pnictides, LnOFeAs/BaFe2As2, are joined (Fig. 1c). The calculated local and average electric potentials for this heterointerface are given in SI, Fig. S7. The hypothetical Ba(Fe1-xCox)2As2/BaFe2As2 interface should be compensated as well; however, this kind of heterointerface becomes obsolete after we find Co-diffusion from the top LnOFe1-xCoxAs into the bottom BaFe2As2 layer.
Originally uncompensated interfaces are subjected to a compensation mechanism of the electric dipole moment, which results in the formation of an interfacial layer. Similar observations were made for Fe-pnictide surfaces. Equivalent compensation mechanisms for uncompensated dipole moments are found in charge reconstruction and modulation31 or in shifts of the Fermi surface upon surface doping.32 The compensation mechanisms at Fe-pnictide heterointerfaces trigger the formation of either a metallic layer (for example, Fe or Ba) or a compound layer, across which an ion valence change occurs (for example, SrTiO3 with Ti3+ or BaFeO3 with a change from Fe4+ to Fe2+). This situation can be observed whenever Fe-pnictides are grown on top of an insulating, nonpolar (or weakly polar) material. Examples include BaFe2As2/SrTiO3 (Fig. 1d, e), BaFe2As2/(La,Sr)(Al,Ta)O3 (Fig. 1f), and BaFe2As2/MgO (Fig. 1g).
The Ln-1111/Ba-122 heterointerface as a test bed
In contrast to previous studies dealing with polar/metal and polar/insulating combinations, we introduce here the heterointerface between two polar Fe-pnictide compounds, in particular, quaternary LnOFeAs (Ln = La, Sm; “Ln-1111” with a ZrCuSiAs-type structure) and ternary BaFe2As2 (“Ba-122” with a ThCr2Si2-type structure). Both share common structural features, such as [Fe2As2]2− layers, a similar a-axis, and ionic bonding along the c-axis direction and, therefore, support epitaxial growth.33 Since the Ln-1111/Ba-122 interface does not interrupt the sequential stacking of layers with an alternating layer charge ±2, it avoids a polarization discontinuity. HRTEM proves that the commonly shared [Fe2As2]2− layer constitutes a clean heterointerface after joining the Ln-1111 and Ba-122 unit cells with atomic precision, as suggested by calculations of the local electric potential.
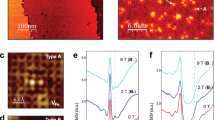
Consideration of the polarity allows the prediction of the interface microstructure, particularly if IFLs are needed to compensate for charges and dipole moments. With the addition of different ionic constituents, the electrostatic conditions in Fe-pnictide layers can be either preserved or perturbed. Therefore, we subjected the Ln-1111/Ba-122 heterointerface in one case to an additional Co2+ supply and in another case to excess O2− during deposition. For this purpose, we selected different target compositions for LnO1-yFe1-xCoxAs (Ln = La, Sm and x = 0, 0.15; y = 0, 0.1) to continue film growth on Ba-122. The results demonstrate the proof-of-principle: clean and smooth interfaces were obtained for the undoped (Fig. 2a, d, g) and Co2+-substituted cases (Fig. 2b, e), whereas an IFL of higher roughness was formed with excess O2− (Fig. 2c, f, h). In the following, we present and discuss the two different cases in detail. Our study is based on the results for six heterostructures investigated by XRD, XRR, STEM, EELS, electron-dispersive spectroscopy (EDS), AES, and electrical transport measurements.
a clean, undoped Sm-1111/Ba-122 interface, b clean, Co2+-substituted La-1111/Ba-122 interface; c interface layer (IFL) formation in Sm-1111/Ba-122 with excess O2–. AES depth profiles across the interface for d undoped Sm-1111/Ba-122, e Co2+-substituted La-1111/Ba-122, and f Sm-1111/Ba-122 with excess O2–. Note the interface layer region with a high O content and lower As content. XRR intensity oscillations reveal the different interface roughnesses of g the originally compensated and clean Sm-1111/Ba-122 interface and h) the originally uncompensated interface in the presence of excess O2–.
Originally compensated and coherent Ln-1111/Ba-122 interface
According to the above prediction, clean and coherent interfaces with a commonly shared [Fe2As2] layer are found with HAADF-STEM for undoped Sm-1111/Ba-122 as well as for Co-substituted La-1111/Ba-122. Figure 3 exemplarily summarizes the microstructural investigations of the latter. Co2+ ions supplied during Ln-1111 deposition do not perturb layer charges or interface polarity because they easily substitute for Fe2+. AES depth profiling further confirms the diffusion of Co2+ ions from the top into the bottom layer (SI, Fig. S3).
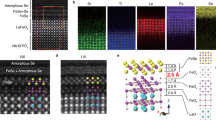
a–c HAADF-STEM of LaOFe1-xCoxAs/Ba(Fe1-xCox)2As2 lamella prepared by conventional milling showing from top to bottom the LaOFe1-xCoxAs layer, the coherent interface with the shared [Fe2As2] layer (black arrows), and the bottom Ba(Fe1-xCox)2As2 layer. The electron beam is parallel to the [100] direction of the Fe-pnictides. d Locally (STEM) determined interlayer spacings across the heterostructure compared with globally (XRD) determined lattice parameters. The DFT calculated values of the interfacial unit cell are shown as green full circles. The lattice plane spacing dFe-Fe;IIc jumps by 2.9 ± 0.5 Å at the interface. e Electron energy loss (EELS) spectra for an energy loss range E = 688.0–892.7 eV. f VDF images for the La-1111, Ba-122, and MgO structures combined into a three-color image; g–i representative diffraction patterns for La-1111, faulted region, Ba-122 and MgO; j HAADF-STEM image of the La-1111/Ba-122 interface showing some faulting and an unclear structure; k HAADF-STEM image of the Ba-122/MgO interface showing a sharp and well-defined interface; l elemental composition traces (EDS) across one such area (not exactly the same as in the images) in the same orientation as the images. See SI for further details.
The atomic resolution of the HAADF-STEM images (Fig. 3a–c) allows the evaluation of the distances between two successive [Fe2As2] layers, dFe-FeIIc, and the local c-axis lattice parameters across the interface and in its vicinity (Fig. 3d). The distance between the last Ba plane in Ba-122 and the first La plane in La-1111 is 6.65 ± 0.28 Å. The c-axis lattice parameters determined by XRD reveal that c1111,XRD = 8.76 Å (La-1111) and ½c122,XRD = 6.47 Å (Ba-122); these values are close to the interfacial distances from the optimized DFT calculations (8.79 and 6.57 Å, respectively). The interfacial matching mostly affects the lattice parameters of the last row of Ba-122 and the first row of La-1111 unit cells. Both unit cells share a common a-axis lattice parameter at the interface with a = 4.22 Å and are additionally elongated in the c-axis direction with c122 = 13.0 ± 0.2 Å (from dBa-Ba) and c1111 = 9.25 ± 0.55 Å (from dLa-La). Compared to the averaged c-axis lattice parameters from XRD, the locally determined interfacial c-axis lattice parameters are 0.5% larger for Ba-122 and up to 5.5% larger for La-1111. The interface itself is characterized by an abrupt change in the c-axis lattice parameters, and the separation of Fe planes, dFe-FeIIc, jumps from 6.8 to 9.5 Å when going from Ba-122 to La-1111.
In addition to Co-diffusion, the cation interdiffusion of Ba2+ and La3+ ions traced by EELS reaches at least 5 nm deep into the adjacent layers (Fig. 3e). The change in the intensities of the Fe L2,3, Ba M4,5, and La M4,5 edges is mapped for different positions across the La-1111/Ba-122 interface (red) and traces a locally confined La3+ ↔ Ba2+ interdiffusion. The Co L2,3 edges (very close to the Ba M4,5 edges) cannot be resolved in this measurement. The ionic radius of Ba2+ being larger than that of La3+ could partially explain the increase in interfacial unit cell volumes; however, while La substitution in BaFe2As2 films is documented,34 the structural stability of LaOFeAs is expected to be limited when Ba2+ substitutes for La3+.
The Co-substituted La-1111/Ba-122 heterostructure was analyzed by both SPED and HAADF-STEM combined with EDS mapping across the interface. Figure 3f–l shows the results of this analysis. SPED reveals distinct diffraction patterns for the different layers. The resulting four-dimensional dataset of two real space and two reciprocal space dimensions35 can then be processed to show the spatial distribution of each exemplar diffraction pattern.11 There are clearly three diffraction patterns: for MgO, for Ba-122, and for the La-1111 structure (Fig. 3g–i). These are all different enough that the spots can be isolated, and the spatial distribution of these three patterns can be easily mapped as VDF images (Fig. 3f).
Since a small amount of O2− impurity cannot be entirely excluded, there are regions at the top of the Ba-122 layer that are faulted. As a result, some of the produced diffraction patterns are complex and appear to resemble a mixture of the 122 and 1111 diffraction patterns, and as such, this region cannot be mapped as a separate pattern. Figure 3j–k shows HAADF-STEM images of the two interfaces. The Ba-122/MgO interface is typically perfect and coherent and only shows few defects (although there is a darker region in the center of Fig. 3f showing a growth defect with a less clear structure). On the other hand, the La-1111/Ba-122 interface also has some faulted regions where the structure is less clear and may not be the same through the thickness of the lamella examined in the TEM. The EDS traces in the direction perpendicular to the interfaces are compared in Fig. 3l. The EDS traces do not contain Co, as the Co-Kα line cannot be separated from the much stronger Fe-Kβ and the Co-Kβ is too weak to use.
Interface layer formation in Sm-1111/Ba-122 with excess O2–
The microstructure and electronic properties change drastically in the case of excess O2– during Sm-1111 deposition. As a result of the perturbed interface polarity in the presence of excess O2–, IFL formation between Ba-122 and Sm-1111 is observed in the respective heterostructures by AES depth profiling, TEM-EDS analysis (Fig. 4), and XRR (Fig. 2e). Figure 4 summarizes the microstructural results of the Sm-1111/IFL/Ba-122 heterostructure. Sm-1111 grows on top of a rough IFL that is up to 9–10 nm in thickness (Fig. 4a).
a STEM brightfield (BF) image of the Sm-1111/IFL/Ba-122 cross-section. The roughness of the IFL is visible in the contrast. b HR-STEM BF image of the IFL showing crystalline structures. c EDS analysis with As L, O K, Sm L, Fe K, and Ba L maps confirms the presence of O, Sm, and Fe in the IFL. Horizontal lines mark the IFL region.
Combined HRTEM and EDS reveal the presence of a crystallographic phase rich in Sm, Fe, and O in the IFL (Fig. 4b, c). Simultaneously, the absence of As and Ba is confirmed. We attribute the formation of an Sm-Fe-O-containing interfacial layer to the oversupply of O2– and its inability to substitute for another anion site, i.e., As3–.
A similar mechanism was previously reported for the Ba(Fe1-xCox)2As2/(La,Sr)(Al,Ta)O3 interface.36 Although the exact atomic arrangement is not entirely known, Fe-pnictides bond on an interfacial Fe layer on top of a Ba-diffused (La,Sr)(Al,Ta)O3 surface layer. The absence of As in this interface is noted. In the Sm-1111/IFL/Ba-122 heterostructure, the interfacial layer consumes excess O with Sm and Fe, while As is not incorporated.
Impact on superconductivity
The electrical resistance and superconducting properties of the different Ln-1111/Ba-122 heterostructures display interesting variations (Fig. 5 and Fig. S8). While the undoped Sm-1111/Ba-122 heterostructure does not become superconducting (Fig. 5b),37 Co2+ supply during Ln-1111 deposition and Co2+ diffusion lead to electron doping of the originally undoped Ba-122 layer (Fig. 5a). AES traces the Co LMM signal in the whole heterostructure from the top down to the substrate. The final Co concentration depends on the Co2+ supply during film growth and the layer thicknesses. The measured critical temperatures also exceed the maximum Tc = 13–18 K in LnOFe1-xCoxAs (Ln = La, Sm).38 Co-diffusion during film growth balances the Co content in the individual Fe-pnictide layers. We find average Co contents of 0.08 ± 0.02 (in La-1111/Ba-122) and 0.06 ± 0.03 (in Sm-1111/Ba-122) when starting with x = 0.15 in the LnOFe1-xCoxAs target. The observations of Tc,90 = 16.5–20.5 K are close to optimal doping in Ba-122. Furthermore, the 3D superconducting state is traced by the angular dependence of the upper critical field, which according to the anisotropic Ginzburg-Landau (AGL) theory is µ0Hc2 = µ0Hc2//ab/(cos2θ + γ2sin2θ)0.5, where γ = Hc2//ab/Hc2//c and θ is the angle between the ab-planes and the applied magnetic field (Fig. 5d, e). The Co-substituted heterostructures have an overly low Hc2 anisotropy of γ = 2.0 ± 0.1. The observation of Co-diffusion through the interface also suggests that the interface in Ba(Fe1-xCox)2As2/BaFe2As2:O heterostructures is obsolete and that the heterostructure is rather a case of homoepitaxial Ba-122/Ba-122 growth.
a in the presence of Co doping and b for undoped layers, and c the metal-to-superconductor transition with time in the heterostructure with interfacial layer formation. The undoped heterostructure in (b) does not develop superconductivity after time but shows a slightly increased resistance (curves 1, 2). (See also Fig. S8 in SI.) d, e Ginzburg-Landau fit (red curve) for the upper critical fields in Co-doped heterostructures showing 3D superconductivity (90% Rn). f 2D-induced superconducting state in the heterostructure with an interfacial layer fitted by Tinkham’s formula (blue) (80% Rn).
With excess O2–, we find not only interfacial layer formation between Sm-1111 and Ba-122 but also the gradual development of a metal-to-superconductor transition with time (Fig. 5c). We repeat AES analysis of this heterostructure 6 months after growth but cannot detect any changes in the elemental concentration. A complete transition develops after 240 days after growth, with Tc,90 = 27.5 K. At present, the superconducting mechanism in this heterostructure is unclear, but compared to the Co-substituted variants, the higher Tc is indicative of sufficient doping with less disorder at the Fe sites due to the absence of transition metal substitution. The angular dependence of the upper critical field deviates from the 3D AGL fit and approaches a 2D-like behavior described by Tinkham’s formula (Fig. 5f).39 The induced metal-to-superconducting transition in heterostructures with IFL appears regardless of whether the heterostructure is stored in air or in a desiccator.
Conclusions
We introduced a comprehensive classification of Fe-pnictide heterointerfaces by taking their polar character into account. Originally compensated heterointerfaces appear on metallic layers or on other polar compounds, whereas originally uncompensated heterointerfaces develop an interfacial layer that is required for electrical charge and dipole compensation. The proposed classification facilitates the prediction of the microstructure of heterointerfaces and can be used as an engineering tool. We successfully applied this concept to realize a polar/polar heterointerface in Ln-1111/Ba-122 on a common [Fe2As2] layer. In a series of Ln-1111/Ba-122, we demonstrated different responses of the interface to the presence of impurity cations/anions. While Co2+ additions substitute at the Fe2+ sites and preserve the layer charges, nonsubstitutional excess O2– is not incorporated into the layered Fe-pnictide compounds. This results in drastic modifications of the microstructure and the formation of an interfacial layer. The different Ln-1111/Ba-122 heterointerfaces also show tunability with respect to the superconducting state in Fe-pnictides: in the presence of Co2+ substitution, 3D superconductivity is found after diffusion in the whole heterostructure, whereas a metal-to-superconductor transition and a 2D superconducting state appear with time in Sm-1111/IFL/Ba-122.
References
Wang, Q.-Y. et al. Interface-induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3. Phys. Lett. 29, 037402 (2012).
He, S. et al. Phase diagram and electronic indication of high-temperature superconductivity at 65 K in single-layer FeSe films. Nat. Mater. 12, 605–610 (2013).
Tan, S. et al. Interface-induced superconductivity and strain-dependent spin density waves in FeSe/SrTiO3. Nat. Mater. 12, 634–640 (2013).
Lee, D.-H. Routes to high-temperature superconductivity: a lesson from FeSe/SrTiO3. Annu. Rev. Condens. Matter Phys. 9, 261–282 (2018).
Huang, D. & Hoffman, J. Monolayer FeSe on SrTiO3. Annu. Rev. Condens. Matter Phys. 8, 311–336 (2017).
Haindl, S., Kinjo, H., Hanzawa, K., Hiramatsu, H. & Hosono, H. Pulsed laser deposition of SmFeAsO1-δ on MgO(100) substrates. Appl. Surf. Sci. 437, 418–428 (2018).
Haindl, S., Sato, M., Wurmehl, S., Büchner, B. & Kampert, E. Pulsed laser deposition of Fe-oxypnictides: Co- and F-substitution. Supercond. Sci. Technol. 33, 105004 (2020).
MacLaren, I., Nord, M., Jiao, C. & Yücelen, E. Liftout of high-quality thin sections of a perovskite oxide thin film using a xenon plasma focused ion beam microscope. Microsc. Microanal. 25, 115–118 (2019).
Rauch, E. F. et al. Automated nanocrystal orientation and phase mapping in the transmission electron microscope on the basis of precession electron diffraction. Z. Kristallogr. 225, 103–109 (2010).
MacLaren, I. et al. A comparison of a direct electron detector and a high speed video camera for scanning precession electron diffraction phase and orientation mapping. Microsc. Microanal. 26, 1110–1116 (2020).
Paterson, G. W. et al. Fast pixelated detectors in scanning transmission electron microscopy. Part II: post acquisition data processing, visualisation, and structural characterisation. Microsc. Microanal. 26, 944 (2020).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Database codes ICSD 169555. ICSD provided by FIZ Karlsruhe – (Leibniz Institute for Information Infrastructure, 2020).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Haindl, S. et al. Thin film growth of Fe-based superconductors: from fundamental properties to functional devices. A comparative review. Rep. Prog. Phys. 77, 046502 (2014).
Thersleff, T. et al. Coherent interfacial bonding on the FeAs tetrahedron in Fe/Ba(Fe1-xCox)2As2 bilayers. Appl. Phys. Lett. 97, 022506 (2010).
Engelmann, J. et al. Fe/Ba(Fe1-xCox)2As2 multilayers and quasi-multilayers with Tc = 29 K. Phys. C. 494, 185–188 (2013).
Lee, S. Artificially engineered superlattices of pnictide superconductors. Nat. Mater. 12, 392–396 (2013).
Gao, P. et al. Atomic and electronic structures of superconducting BaFe2As2/SrTiO3 superlattices. Phys. Rev. B 91, 104525 (2015).
Kang, J.-H. et al. Control of epitaxial BaFe2As2 atomic configurations with substrate surface terminations. Nano Lett. 18, 6347–6352 (2018).
Kang, J. H. et al. Superconductivity in undoped BaFe2As2 by tetrahedral geometry design. Proc. Natl Acad. Sci. USA 117, 21170–21174 (2020).
Tarantini, C. et al. Artificial and self-assembled vortex-pinning centers in superconducting Ba(Fe1-xCox)2As2 thin films as a route to obtaining very high critical-current densities. Phys. Rev. B 86, 214504 (2012).
Oh, M. J. et al. Vortex pinning in artificially layered Ba(Fe,Co)2As2 film. Cryogenics 92, 1–4 (2018).
Harrison, W. A., Kraut, E. A., Waldrop, J. R. & Grant, R. W. Polar heterojunction interfaces. Phys. Rev. B 18, 4402–4410 (1978).
Hong, S., Nakhmanson, S. M. & Fong, D. D. Screening mechanisms at polar oxide heterointerfaces. Rep. Prog. Phys. 79, 076501 (2016).
Noguera, C. Polar oxide surfaces. J. Phys. Condens. Matter 12, R367–R410 (2000).
Tasker, P. W. The stability of ionic crystal surfaces. J. Phys. C Solid State Phys. 12, 4977–4984 (1979).
Ohtomo, A., Hwang, H. Y. & High-Mobility, A. Electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004).
Kim, S. et al. Surface reconstruction and charge modulation in BaFe2As2 superconducting film. J. Phys. Condens. Matter 30, 315001 (2018).
Kyung, W. S. et al. Enhanced superconductivity in surface-electron-doped iron pnictide Ba(Fe1.94Co0.06)2As2. Nat. Mater. 15, 1233–1236 (2016).
Haindl, S., Hanzawa, K., Sato, H., Hiramatsu, H. & Hosono, H. In-situ growth of superconducting SmO1-xFxFeAs thin films by pulsed laser deposition. Sci. Rep. 6, 35797 (2016).
Katase, T., Iimura, S., Hiramatsu, H., Kamiya, T. & Hosono, H. Identical effects of indirect and direct electron doping of superconducting BaFe2As2 thin films. Phys. Rev. B 85, 140516R (2012).
Ophus, C. Four-dimensional scanning transmission electron microscopy (4D-STEM): from scanning nanodiffraction to ptychography and beyond. Microsc. Microanal. 25, 563–582 (2019).
Iida, K. et al. Scaling behavior of the critical current in clean epitaxial Ba(Fe1-xCox)2As2 thin films. Phys. Rev. B 81, 100507R (2010).
The absence of a doping effect in this heterostructure may indicate that interdiffusion at the interface is suppressed.
Wang et al. Effects of cobalt doping and phase diagrams of LFe1-xCoxAsO (L = La, Sm). Phys. Rev. B 79, 054521 (2009).
Tinkham, M. Effects of fluxoid quantization on transitions of superconducting films. Phys. Rev. 129, 2413–2422 (1967).
Acknowledgements
S.H. and S.N. acknowledge funding from WRHI and discussions with T. Ying. The authors thank J. Matsumoto, T. Katase, H. Hiramatsu, H. Hosono (from Tokyo Institute of Technology), and S. Wurmehl (from IFW Dresden) for the target preparation. The authors thank Mr. W.A. Smith at the University of Glasgow for his assistance with the FIB preparation and Dr. S. McFadzean for his assistance with technical support for the JEOL ARM scanning transmission electron microscope. Drs. Damien McGrouther and Dima Maneuski and Prof. Val O’Shea are gratefully acknowledged for all their work on the development of a Medipix-3 detector in the electron microscope, which became Merlin for the EM system. The authors thank Dr. Gary W. Paterson for his assistance in providing the fpd Python libraries and example Jupyter notebooks for processing the VDF data. The authors thank Dr. Stavros Nicolopoulos, Mr. Alan Robins, Mr. Doug Cosart, Dr. J. K. Weiss, and Dr. Jing Lu at NanoMEGAS for all their assistance with developing the prototype direct detection—SPED system and debugging the software so that data of the quality shown here can routinely be collected. While this work was not directly funded by the EPSRC, it could not have happened without the sustained investment in the development of pixelated STEM and detectors for pixelated STEM by the EPSRC over many years (funding for a broader research project on “Fast Pixel Detectors: a paradigm shift in STEM imaging” (EP/M009963/1), funding from Impact Acceleration Accounts specifically for the integration of the detector into the microscope (EP/K503903/1 and EP/R511705/1), and funding from EPSRC (EP/R511705/1) and NanoMEGAS on the integration of the Merlin for the EM detector with the precession diffraction system).
Author information
Authors and Affiliations
Contributions
S.H. conceived and designed the study and was responsible for thin film growth and film characterization (XRD, AFM, and electrical transport measurements), evaluation of data, and preparation of the manuscript. S.N. was responsible for DFT calculations. Mi.S. carried out AES measurements and the quantification of the results. HAADF-STEM images and EELS data were produced by Ma.S. at the Tokyo Institute of Technology. I.M. at the University of Glasgow was responsible for FIB preparation of samples for TEM/STEM analysis and for performing the TEM and STEM analysis for SPED, EDS mapping, atomic-resolution STEM imaging, and the subsequent data analysis. All authors discussed the results and have approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Haindl, S., Nikolaev, S., Sato, M. et al. Engineering of Fe-pnictide heterointerfaces by electrostatic principles. NPG Asia Mater 13, 67 (2021). https://doi.org/10.1038/s41427-021-00336-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-021-00336-6