Abstract
Electric control of magnetic vortex dynamics in a reproducible way on an ultrafast time scale is a key element in the quest for efficient spintronic devices with low-energy consumption. To be useful, the control scheme should ideally be swift, be scalable, be noninvasive, and result in reliable magnetic switching. Such requirements, particularly the reproducibility of altering the vortex chirality and/or polarity, are not yet met by magnetic vortex switching via external magnetic fields, spin-polarized currents, spin waves, or laser pulses. Here, we demonstrate a novel packaged-skyrmion-mediated vortex switching process driven by a simple sequence of picosecond electrical field pulses via magnetoelectric interactions. Both the vortex chirality and polarity show a well-defined reversal behavior. The unambiguous repeated switching between four different magnetic vortex states provides an energy-efficient, highly localized, and coherent control method for nonvolatile magnetic vortex-based information storage and handling.
Similar content being viewed by others
Introduction
Magnetic vortices are formed in confined soft ferromagnetic structures, such as disks, triangles, squares, and stripes on the micron/submicron scales1,2. The driving force is a subtle competition between the exchange interaction and shape anisotropy in confined geometries. As one kind of topological magnetic defect3, a magnetic vortex is characterized by an in-plane curling magnetization (chirality: either clockwise or counterclockwise) and an out-of-plane nanometer-sized core magnetization (polarity: up or down). Having the simplest topologically nontrivial spin configuration, magnetic vortices exhibit several advantageous features, such as high thermal stability, negligible magnetostatic interactions, and a diversity of information storage for high-density and nonvolatile magnetic memories and spintronic devices4,5. Due to the rotational symmetry of the magnetic vortex and strong exchange interactions in ferromagnetic materials6, it is, however, difficult to reverse the vortex polarity and/or chirality. Alternating magnetic fields7, in-plane magnetic field pulses8, resonant microwave pulses9, field-driven spin waves10, spin-polarized currents11,12, and photothermal-assisted femtosecond laser pulse excitation13 have been used to switch the vortex-core polarity. To solve the problem of chirality switching with magnetic fields, structures with broken symmetry have also been introduced14. While few studies considered the simultaneous control of the vortex chirality and polarity, it turned out to be challenging to precisely determine when core switching occurs, and even worse, the clockwise and counterclockwise vortex states may randomly emerge with a similar occurrence frequency13, thus largely prohibiting the development of reliable magnetic vortex-based spintronics.
To remedy this situation and facilitate the vortex dynamics for ultrafast all-optical magnetism15, in this work, we exploit another feature of noncollinear spin ordering, namely, the magnetoelectric (ME) effect leading to a spin-driven emergent ferroelectric polarization P, which allows an external THz electric-field E(t, r) to couple with and drive the vortex via −E·P. Here, the ME effect is facilitated by the inverse Dzyaloshinskii-Moriya (DM) mechanism16,17 (cf. also the “Magnetoelectric Interaction” section in the Supplementary Information). The ME coupling strength ξm is determined by the spin–orbit interaction and is linearly related to the applied electric field18. In the continuum limit, the net ferroelectric polarization reads P = ξm[(m‧∇)m − m(∇‧m)]19,20. Thus, the additional ME-driven effective field acting on the spin system reads
Here, μ0 is the vacuum permeability, M = Msm, and Ms is the saturation magnetization. For an electric field normal to the magnetic plane (hereafter defined by the ez direction), the first term in Hme acts on the magnetization as the field due to an interfacial DM interaction (DMI)21,22,
The curl of the electric field entering the last term of Hme is expressible via Maxwell’s equation as \(\nabla \times {\mathbf{E = }} - \frac{{\partial {\mathbf{B}}}}{{\partial t}} = - \mu _0\left( {{\mathrm{1}} \, + \, \chi _m^{{\mathrm{ - 1}}}} \right)\frac{{\partial {\mathbf{M}}}}{{\partial t}}\) (where M = Msm and χm is the material magnetic susceptibility23), pointing to an additional route for magnetic energy transfer and processional damping control. Thus, in principle, it is possible to realize all-electric magnetization switching through ME coupling.
In fact, as demonstrated here, ME coupling allows for remarkably swift, detailed, and controlled manipulation of the magnetic vortex configurations by electric means. In addition to achieving a precisely and independently reproducible reversal of the vortex polarity and/or chirality by a simple sequence of feasible asymmetric THz pulses (cf. the inset of Fig. 1a and Supplementary Figs. s1–s2)24,25,26,27,28,29, we observe a new phenomenon, namely, packaged-skyrmion-mediated picosecond switching of a magnetic vortex. This switching does not involve gyrotropic motion with the creation and subsequent annihilation of a vortex–antivortex pair7. In addition to the technological relevance, the results provide deeper insights into the fundamentals of the ME effects and magnetization relaxation dynamics. Furthermore, the findings point to exciting opportunities for exploiting the impressive recent advances in THz sources25,26,27,28,29 for spintronics devices.
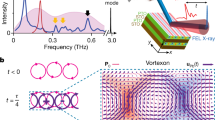
a Phase diagrams of remanent magnetization configurations (I–IX) reached by applying a static Gaussian electric field to initial vortex state I. b Reproducible switching between four magnetic vortex states, I → II → III → IV → I…… (labeled by the corresponding assistant colors in a), by a simple sequence of two time-asymmetric pulses (also referred to as half-cycle pulses, HCPs), Ezp (dotted blue line) and Ezc (solid blue line). Other remaining white areas denote the transition processes without well-defined vortex states. s (black solid line) and c (red solid line) are the skyrmion and chirality numbers of the magnetization configurations, respectively. Inset: the above panel shows the diffraction-limited Gaussian profile spatial intensity distribution of the employed electric-field pulses; the black envelope in the bottom panel shows one cycle of the time profile of an experimentally feasible strongly asymmetric pulse; the blue dotted line is the numerical shape used in simulations. In both cases, the time integral over the pulse duration is zero, as required by the Maxwell equation.
Materials and methods
The magnetization dynamics of a vortex is investigated by finite-difference micromagnetic simulations with GPU acceleration based on the Landau–Lifshitz–Gilbert (LLG) equation30,
where γ is the gyromagnetic ratio and Heff is the effective magnetic field, which includes the isotropic Heisenberg exchange field, the uniaxial magnetocrystalline anisotropy field, the magnetostatic demagnetizing field, and the ME field Heff. In the present study, the material parameters are chosen for permalloy (Py, a magnetically very soft material of great technological importance) at room temperature: exchange constant A = 13 pJ/m, saturation magnetization Ms = 8 × 105 A/m, and magnetocrystalline anisotropy Ku = 0. The Gilbert damping constant is set to α = 0.05, which is larger than the value of a bulk system but is in a reasonable range for a Py thin film31. The ME coupling strength is ξm = 1‧pC/m, which is realistic for Py films prepared on a Pt layer32,33,34,35,36,37 (a detailed discussion can be found in the “Magnetoelectric interaction” and “Magnetic vortex switching of YIG disk” sections in the Supplementary Information). An initially stable magnetic vortex with positive polarity (p = 1) and clockwise chirality (c = 1) is prepared in a typical Py square (width of 99 nm and thickness of 3 nm) without any external magnetic/electric fields (cf. magnetization configuration I in Fig. 1a). The system is discretized by cubic cells with a size of (3 nm)3 during the simulations.
Results
Phase diagram
By sequentially applying two types of time-asymmetric electric-field pulses with different amplitudes and pulse durations to initial state I, we observe an ultrafast and highly reproducible switching between four vortex states, as demonstrated in Fig. 1b (cf. also Supplementary Video S1). The time required for the core polarization reversal is on the order of 15 ps, and that for the chirality reversal is approximately 325 ps. These are very high speeds for magnetic vortex switching, faster than any previously reported speeds achieved by other control schemes38. In addition, the reliable repeatability of the switching process is a clear advantage. With a view toward experimental realization, using a Maxwell solver, we inspected the electromagnetic-field distribution in samples for the THz fields used in the calculations. For the materials, geometries, and sizes of our samples and the intensities and duration of the pulses presented below, it was found that a coupled Maxwell-micromagnetic simulation is not necessary and the procedure detailed below and in the supplementary materials is adequate (cf. the “Electric field distribution in the sample” section and Fig. s3 in the Supplementary information).
For a better understanding, let us first refine the possible stable magnetization configurations under time-independent but spatially inhomogeneous electric fields, meaning a Gaussian profile for a static electric field applied along the z-axis,
Here, R = 51 nm, (Rx, Ry) is the geometric center of the magnetization configuration, and the width of the Gaussian distribution is determined by the parameter k. Perturbing the prepared vortex state I with p = 1 and c = 1 by E(r), the stable topological magnetic configurations can be characterized by the skyrmion number s and the chirality number c as
where ϕ = arctan(my/mx) and \(\chi _{\mathrm{r}} = \frac{1}{{{\mathrm{8}}\pi }}[{\mathbf{m}}_{\mathrm{r}} \cdot \left( {{\mathbf{m}}_{{\mathrm{r}} + \widehat {\mathrm{x}}} \, \times {\mathbf{m}}_{{\mathrm{r}} + \, \widehat {\mathrm{y}}}} \right) + {\mathbf{m}}_{\mathrm{r}} \cdot \left( {{\mathbf{m}}_{{\mathrm{r}} - \widehat {\mathrm{x}}} \, \times {\mathbf{m}}_{{\mathrm{r}} - \widehat {\mathrm{y}}}} \right)]\). For example, a vortex with winding number n = 1 and core polarization p has half-integer skyrmion number s = np/2, while an ideal skyrmion39 (with opposite directions of spins at r → 0 and r → ∞) has integer s = np. In Fig. 1a, we present a more detailed examination of the relaxation into remnant states from initial configuration I under different Gaussian electric fields. In addition to the four desired vortex states (I–IV) and one complex distorted state IX, four new packaged-skyrmion-like stable configurations (V–VIII) emerge in the presence of large and narrow Gaussian electric fields. The skyrmion number of these four new, well-shaped configurations is determined to be less than 0.5 and mostly ~0.3 by integrating χr over the whole square, but it may approach ±1 if the radius of the integral area is shrunk to ~0.7 halfwidth of the corresponding Gaussian field. From the topological point of view, these packaged skyrmions with localized topological charge |s| = 1 are very important for switching between the s = ±1/2 topological sectors, as shown in the following figures, and they indeed dynamically occur during the vortex switching processes, assisting the polarity and chirality reversal.
The phase diagrams suggest the following possible vortex transitions by applying different amplitude (Ez) and halfwidth (k) electric fields: (i) core polarization reversal from state I (s = 1/2 and c = 1) to IV (s = −1/2 and c = 1), (ii) chirality reversal from state I (s = 1/2 and c = 1) to III (s = 1/2 and c = −1), and (iii) simultaneous polarity and chirality reversal from state I (s = 1/2 and c = 1) to II (s = −1/2 and c = −1). However, it should be noted that the dynamic switching processes are inessential. The transition conditions in the phase diagrams are mainly determined by external parameters: the pulse amplitude and the pulse duration.
Vortex-core switching
The details of the magnetization dynamics of the vortex-core reversal processes, including the time evolution of the ME field, are demonstrated in Fig. 2a (see also Supplementary Video S2). The pulses we employ are generally feasible. In fact, much shorter and stronger pulses have been reported (for instance ref. 40). The pulse consists of one strong and short part (which we call the head) and a much longer and weaker part with opposite polarity (which we call the tail). As shown in full detail in ref. 24, as long as the duration of the head is shorter than the typical time scale of the system (here, the processional period), then the exact shape of the pulse is subsidiary.
a Time-resolved micromagnetic simulations showing the dynamic configurations of the magnetization and perpendicular effective ME fields. The dynamic process of vortex switching can be effectively described by the time evolution of the skyrmion number (s, black solid line) and the chirality number (c, red solid line). b Reproducible control of the vortex polarity. Two vortex states (I and IV) with opposite core polarizations are labeled with the same color scheme used in Fig. 1.
In the typical case shown in Fig. 2a, we observe that as the strong (50 MV/cm) and short (15 ps) head part of the asymmetric HCP (k = 6) reaches initial vortex I, an ME field with a positive core but negative circling is dynamically induced. With time, this effective magnetic field reverses its direction, and a temporal packaged-skyrmion (VII) develops, reaching full formation at approximately 14 ps (before the pulse tail). Eventually, the packaged-skyrmion decays into spin waves, and vortex IV with opposite polarity is stabilized during the weak (5 MV/cm) and long (150 ps) tail of the HCP. Vortex IV can be switched back to vortex I by a second sequence (same type) pulse following very similar processes, \({\mathrm{IV}}\mathop{\longrightarrow}\limits^{{{\mathrm{VIII}}}}{\mathrm{I}}\) with the emission of spin waves. These vortex polarity reversals show very high and reliable reproducibility, as demonstrated in Fig. 2b and Supplementary Video S3. Clearly, the underlying mechanism is different from the usual gyrotropic core excitation, in which the vortex-core switching dynamics involves the creation and annihilation of a vortex–antivortex pair, accompanied by the injection of a magnetic monopole7,8,9,41. Here, the change in the topological charge ∆s = ±1 between the two vortex states occurs through the formation of the intermediate packaged-skyrmion with highly localized skyrmion number s = ±1. It is worth emphasizing that the core reversal speed can be further enhanced by a stronger and/or shorter time-asymmetric electric-field pulse. This is particularly useful from the application point of view, as short pulses cause less material damage.
Vortex chirality reversal
In terms of applications, chirality switching is highly desirable for storing two bits of digital information in magnetic vortex-based devices. Chirality is akin to symmetry and can be changed in many cases by introducing asymmetry into ferromagnetic disks, such as masked disk42, odd-side regular polygonal nanomagnets43, and rectangular thin films with an aspect ratio of 2:144. However, such methods cannot be applied to a symmetric square disk with an even number of sides due to the symmetrical nucleation energy during vortex formation. Yakata et al. proposed an alternative method for controlling the vortex chirality in square permalloy dots via the circular Oersted field45. Here, we show that vortex chirality reversal can also be simply realized by using time-asymmetric electric-field pulses. Compared with vortex-core reversal, chirality switching requires relatively weak and long HCPs with small k. Figure 3 and Supplementary Video S4 evidence the only-chirality switching via HCPs with a peak amplitude of 10 MV/cm and a duration of 450 ps. The slower part of the HCP peaks at 2.5 MV/cm and has a duration of 1800 ps. A short time after the excitation of vortex I, a hedgehog skyrmion without preferred chirality develops, and the skyrmion number reaches its maximum of s ≈ 1 at ~190 ps. This unstable (global) Néel-type skyrmion then relaxes into vortex state III before the end of the HCP’s head (450 ps), at which the vortex chirality has been completely reversed. Such a vortex state (III) survives the pulse tail and becomes more stable through the emission of spin waves. Similar to vortex-core switching, well-defined reproducible chirality switching can be realized by two inversion recovery pulse sequences (see Fig. 3b and Supplementary Video S5).
a Time evolution of the skyrmion and chirality numbers driven by the Gaussian pulse (k = 1) sequences with opposite field directions. Snapshot images illustrating the in-plane ME field (above) and magnetization configuration (below) at different stages of the vortex dynamics. b Reliable chirality switching between stable vortex states I (s = 1/2 and c = 1) and III (s = 1/2 and c = −1) by the same HCPs as in a.
Simultaneous control of vortex polarity and chirality
As demonstrated in Fig. 4b and Supplementary Video S6, we find that by only slightly shortening the pulse duration to terminate the relaxation from the hedgehog skyrmion to vortex state III (cf. Fig. 3a), the skyrmion completely dissolves after the peak pulse. The reversed chirality, however, persists into the pulse tail, and the magnetic core is also reversed relatively soon after the chirality reversal. Vortex configuration II emerges and is then stabilized by releasing spin waves. The simultaneous control of the vortex core and chirality shows a highly reliable repeatability, I → II → I…… (cf. Fig. 4b and Supplementary Video S7).
a Relatively short HCPs compared to those in Fig. 3 are used to simultaneously reverse the vortex polarity and chirality. The vortex dynamics before 325 ps is the same as that shown in Fig. 3a, and different and important behavior is illustrated in the snapshots after 325 ps. b Vortex switching between vortex state I (s = 1/2 and c = 1) and vortex state II (with opposite vortex polarity and chirality, i.e., s = −1/2 and c = −1).
Furthermore, it is also possible to obtain independent switching between two random vortex states. Efficient and reliable manipulation of four magnetic vortex states is achievable by any two combinations of the above three switching procedures. For instance, as shown in Fig. 1b, the vortex switching contains in total two predictable dynamic procedures, I → II → III → IV → I…… However, to ensure a more stable hybrid modulation of the vortex, a 42.5 ps interval is set between each pulse.
Evidently, D = ξmEz determines the effective ME field Hme. For a small ME coupling constant ξm, one can obtain a sufficiently large switching field by applying strong electric-field pulses. Detailed investigations show that the switching energy barriers during the reversals of the vortex core and chirality are mainly determined by the exchange energy and the demagnetization energy, respectively. For the YIG disks with a relatively small exchange constant A = 3 pJ/m, saturation magnetization Ms = 1.4 × 105 A/m, and ME coupling constant ξm = 0.5 pC/m, reliable switching of the vortex core and chirality are obtained under weaker electric-field pulses (cf. Figs. s4 and s5 in the “Magnetic vortex switching of YIG disk” section in the Supplementary Information).
Discussions
In the quest for ultrafast optical switching of the magnetic order (refs. 15,46 and references therein), THz fields such as those employed here were demonstrated to be a powerful tool47,48. Pulsed THz driving also allows for new schemes of noninvasive nonprocessional switching49. The fantastic advances in generating and controlling such pulses in the near-field (for instance, via plasmonic structures)25,26,27,28,29 call for exploiting them for data writing/deletion and moving of bits stored in topological magnetic excitations such as magnetic vortices. The intrinsic magnetoelectric interaction that stems from the spin noncollinearity in magnetic vortices serves for coupling to the electric-field component of the THz pulse. In our simulations, we used a sequence of time-asymmetric pulses. The actual shape of the pulse is, however, not decisive; only the time asymmetry and peak field value matter24. The time asymmetry is related to the ratio of the durations of the positive and negative polarity parts of the pulse. Hence, the phenomena predicted here are robust to reasonable variations in the pulse characteristics, ensuring reliable operation of vortex-based data storage. In addition to this advantageous feature, the reproducibility of the picosecond switching of the magnetic vortex polarity and chirality by a simple sequence of THz pulses is also useful. The topological protection and the speed restriction on vortex-core switching can be lifted when forming and utilizing packaged skyrmions. Unlike gyrotropic excitation, the packaged-skyrmion-driven switching of the magnetic vortex does not involve displacement of the vortex core, which bears a great advantage for ultrafast magnetic recording. Spatially localized THz fields, as realized in near-field optics, are advantageous for vortex-core reversal. This points to using plasmonic near fields for vortex steering. Far fields are also useful for vortex chirality control but are diffraction-limited (as also assumed in this work). It is, however, possible to go beyond the diffraction limit by using a normal metal mask or SNOM techniques50. The independent reversal of the vortex polarity and chirality presented here demonstrates a straightforward tool for electric-field control of vortex states. Thus, the current findings for dynamic magnetic vortex switching are of direct and significant relevance for optical-based ultrafast spintronics.
References
Shinjo, T., Okuno, T., Hassdorf, R., Shigeto, K. & Ono, T. Magnetic vortex core observation in circular dots of permalloy. Science 289, 930–932 (2000).
Wachowiak, A. et al. Direct observation of internal spin structure of magnetic vortex cores. Science 298, 577–580 (2002).
Braun, H.-B. Topological effects in nanomagnetism: from superparamagnetism to chiral quantum solitons. Adv. Physiol. Edu. 61, 1–116 (2012).
Bader, S. D. Colloquium: opportunities in nanomagnetism. Rev. Mod. Phys. 78, 1–15 (2006).
Pigeau, B. et al. A frequency-controlled magnetic vortex memory. Appl. Phys. Lett. 96, 132506 (2010).
Usov, N. A. & Kurkina, L. G. Out-of-plane stray field at magnetization reversal in epitaxial magnetite thin films. J. Magn. Magn. Mater. 242345, 1005 (2002).
Waeyenberge, B.-V. et al. Magnetic vortex core reversal by excitation with short bursts of an alternating field. Nature 444, 461 (2006).
Hertel, R., Gliga, S., Fähnle, M. & Schneider, C. M. Ultrafast nanomagnetic toggle switching of vortex cores. Phys. Rev. Lett. 98, 117201 (2007).
Pigeau, B. et al. Optimal control of vortex-core polarity by resonant microwave pulses. Nat. Phys. 7, 26–31 (2010).
Kammerer, M. et al. Magneticvortex core reversal by excitation of spin waves. Nat. Commun. 2, 279 (2011).
Yamada, K. et al. Electrical switching of the vortex core in a magnetic disk. Nat. Mater. 6, 270–273 (2007).
Pribiag, V. S. et al. Magnetic vortex oscillator driven by d.c. spin-polarized current. Nat. Phys. 3, 498 (2007).
Fu, X. et al. Optical manipulation of magnetic vortices visualized in situ by Lorentz electron microscopy. Sci. Adv. 4, eaat3077 (2018).
Tobik, J., Cambel, V. & Karapetrov, G. Dynamics of vortex nucleation in nanomagnets with broken symmetry. Phys. Rev. B 86, 134433 (2012).
Kimel, A. V. & Li, M. Writing magnetic memory with ultrashort light pulses. Nat. Rev. Mater. 4, 189–200 (2019).
Eerenstein, W., Mathur, N. D. & Scott, J. F. Multiferroic and magnetoelectric materials. Nature 442, 759–765 (2006).
Tokura, Seki, S. & Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 77, 076501 (2014).
Liu, T. & Vignale, G. Electric control of spin currents and spin-wave logic. Phys. Rev. Lett. 106, 247203 (2011).
Mostovoy, M. Ferroelectricity in spiral magnets. Phys. Rev. Lett. 96, 067601 (2006).
Jia, C.-L., Onoda, S., Nagaosa, N. & Han, J. H. Microscopic theory of spin-polarization coupling in multiferroic transition metal oxides. Phys. Rev. B 76, 144424 (2007).
Bogdanov, A. N. & Rößler, U. K. Chiral symmetry breaking in magnetic thin films and multilayers. Phys. Rev. Lett. 87, 037203 (2001).
Mulkers, J. et al. Effect of boundary-induced chirality on magnetic textures in thin films. Phys. Rev. B 98, 064429 (2018).
Hickey, M. & Moodera, J. Origin of intrinsic Gilbert damping. Phys. Rev. Lett. 102, 137601 (2009).
Moskalenko, A. S., Zhu, Z.-G. & Berakdar, J. Charge and spin dynamics driven by ultrashort extreme broadband pulses: a theory perspective. Phys. Rep. 672, 1–82 (2017).
Shay, K.-Z., Mai, T., Sharly, F., Daniel, M. M. & Tal, E. Generation of spatiotemporally tailored terahertz wavepackets by nonlinear metasurfaces. Nat. Commun. 10, 1778 (2019).
Lee, Y.-S. Principles of Terahertz Science and Technology. (Springer, New York, 2009).
Mittleman, D. M. Perspective: terahertz science and technology. J. Appl. Phys. 122, 230901 (2017).
Welsh, G. H. & Wynne, K. Generation of ultrafast terahertz radiation pulses on metallic nanostructured surfaces. Opt. Express 17, 2470–2480 (2009).
Luo, L. et al. Broadband terahertz generation from metamaterials. Nat. Commun. 5, 3055 (2014).
Zhu, R. Accelerate micromagnetic simulations with GPU programming in MATLAB. arXiv 1501, 07293 (2015).
Tserkovnyak, Y., Brataas, A. & Bauer, G. E. W. Enhanced gilbert damping in thin ferromagnetic films. Phys. Rev. Lett. 88, 117601 (2002).
Wang, X.-G., Chotorlishvili, L., Guo, G.-H., Jia, C.-L. & Berakdar, J. Thermally assisted skyrmion drag in a nonuniform electric field. Phys. Rev. B 99, 064426 (2019).
Risinggård, V., Kulagina, I. & Linder, J. Electric field control of magnon-induced magnetization dynamics in multiferroics. Sci. Rep. 6, 31800 (2016).
Stashkevich, A. A. et al. Experimental study of spin-wave dispersion in Py/Pt film structures in the presence of an interface Dzyaloshinskii-Moriya interaction. Phys. Rev. B 91, 214409 (2015).
Kostylev, M. Interface boundary conditions for dynamic magnetization and spin wave dynamics in a ferromagnetic layer with the interface Dzyaloshinskii-Moriya interaction. J. Appl. Phys. 115, 233902 (2014).
Kundu, A. & Zhang, S. Dzyaloshinskii-Moriya interaction mediated by spin-polarized band with Rashba spin-orbit coupling. Phys. Rev. B 92, 094434 (2015).
Di, K., Zhang, V. L., Lim, H. S., Ng, S. C. & Kuok, M. H. Direct observation of the Dzyaloshinskii-Moriya interaction in a Pt/Co/Ni film. Phys. Rev. Lett. 114, 047201 (2015).
Zheng, Y. & Chen, W. J. Characteristics and controllability of vortices in ferromagnetics, ferroelectrics, and multiferroics. Rep. Prog. Phys. 80, 086501 (2017).
Tretiakov, O. A. & Tchernyshyov, O. Vortices in thin ferromagnetic films and the skyrmion number. Phys. Rev. B 75, 012408 (2007).
Hassan, M. T. et al. Optical attosecond pulses and tracking the nonlinear response of bound electrons. Nature 530, 66–70 (2016).
Thiaville, A., García, J., Dittrich, R., Miltat, J. & Schrefl, T. Micromagnetic study of Bloch-pointmediated vortex core reversal. Phys. Rev. B 67, 094410 (2003).
Gaididei, Y., Sheka, D. D. & Mertens, F. G. Controllable switching of vortex chirality in magnetic nanodisks by a field pulse. Appl. Phys. Lett. 92, 012503 (2008).
Yakata, S., Miyata, M., Nonoguchi, S., Wada, H. & Kimura, T. Control of vortex chirality in regular polygonal nanomagnets using in-plane magnetic field. Appl. Phys. Lett. 97, 222503 (2010).
Li, J. et al. The control of magnetic vortex state in rectangular nanomagnet. J. Magn. Magn. Mater. 451, 379–384 (2018).
Yakata, S. et al. Chirality control of magnetic vortex in a square Py dot using current-induced Oersted field. Appl. Phys. Lett. 99, 242507 (2011).
Kampfrath, T. et al. Coherent terahertz control of antiferromagnetic spin waves. Nat. Photonics 5, 31–34 (2011).
Yang, Y. et al. Ultrafast magnetization reversal by picosecond electrical pulses. Sci. Adv. 3, e1603117 (2017).
Schlauderer, S. et al. Huber Temporal and spectral fingerprints of ultrafast all-coherent spin switching. Nature 569, 383–387 (2019).
Sukhov, A. & Berakdar, J. Local control of ultrafast dynamics of magnetic nanoparticles. Phys. Rev. Lett. 102, 057204 (2009).
Bazylewski, P., Ezugwu, S. & Fanchini, G. A review of three-dimensional scanning near-field optical microscopy (3D-SNOM) and its applications in nanoscale light management. Appl. Sci. 7, 973 (2017).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Nos. 91963201, 11834005, and 11474138), the German Research Foundation (Nos. SFB 762 and SFB TRR227), the Program for Changjiang Scholars and Innovative Research Team in University (No. IRT-16R35), and the Ministry of Science and Technology of China through grant CN-SK-8-4.
Author information
Authors and Affiliations
Contributions
C.J. and J.B. conceived and supervised the research project and wrote the manuscript. D.Y. performed the micromagnetic simulations with the help of J.K. All authors discussed and analyzed the results and contributed to the final version of the manuscript.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yu, D., Kang, J., Berakdar, J. et al. Nondestructive ultrafast steering of a magnetic vortex by terahertz pulses. NPG Asia Mater 12, 36 (2020). https://doi.org/10.1038/s41427-020-0217-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-020-0217-8