Abstract
Applying a temperature gradient in a magnetic material generates a voltage that is perpendicular to both the heat flow and the magnetization. This phenomenon is the anomalous Nernst effect (ANE), which was long thought to be proportional to the value of the magnetization. However, more generally, the ANE has been predicted to originate from a net Berry curvature of all bands near the Fermi level (EF). Subsequently, a large anomalous Nernst thermopower (\({\boldsymbol{S}}_{{\boldsymbol{yx}}}^{\boldsymbol{A}}\)) has recently been observed in topological materials with no net magnetization but a large net Berry curvature [Ωn(k)] around EF. These experiments clearly fall outside the scope of the conventional magnetization model of the ANE, but a significant question remains. Can the value of the ANE in topological ferromagnets exceed the highest values observed in conventional ferromagnets? Here, we report a remarkably high \({\boldsymbol{S}}_{{\boldsymbol{yx}}}^{\boldsymbol{A}}\)-value of ~6.0 µV K−1 in the ferromagnetic topological Heusler compound Co2MnGa at room temperature, which is approximately seven times larger than any anomalous Nernst thermopower value ever reported for a conventional ferromagnet. Combined electrical, thermoelectric, and first-principles calculations reveal that this high-value of the ANE arises from a large net Berry curvature near the Fermi level associated with nodal lines and Weyl points.
Similar content being viewed by others
Introduction
Conventional thermoelectric devices are based on the Seebeck effect in a two-terminal geometry, where two electronic reservoirs at different temperatures result in an electric voltage that arises in the direction of the imposed temperature gradient1,2. For applications, however, this configuration has considerable drawbacks because the heat reservoir is forced to be part of the electrical circuit. The problem is achieving good thermal insulation while maintaining good electrical conduction. To circumvent this issue, multiterminal thermoelectric devices have recently attracted increasing attention3,4,5,6,7,8,9,10,11,12,13 because they allow for the spatial separation of the heat reservoir from the electric circuitry. One possible implementation of this kind is based on the Nernst effect, which is the generation of a transverse thermoelectric voltage by a temperature gradient and a magnetic field, applied normal to each other14,15,16. Nernst devices are, in principle, simpler to integrate technologically than conventional thermoelectrics because there is no need for both p- and n-type materials.
A ferromagnetic material that generates an anomalous transverse voltage mutually perpendicular to both heat current and magnetization demonstrates the so-called anomalous Nernst effect (ANE)3,4,17,18,19,20. In contrast to the ordinary Nernst effect, the ANE increases rapidly in a low magnetic field. Thus, ANE can give rise to a large Nernst thermopower at a low magnetic field. The ANE is the thermoelectric counterpart of the anomalous Hall effect (AHE) and was first observed in topologically trivial ferromagnets. Therefore, it was believed for a long time that the ANE is proportional to the magnetization of a material itself. Despite many efforts, the maximum value of anomalous Nernst thermopower in ferromagnetic systems is limited and bound to below ~1 µV K−19. However, it was recently found that the AHE is not directly related to the magnetization of a material but is derived more generally from the Berry curvature [Ωn(k)] of the bands near the Fermi level (EF)5,6. This outcome was realized along with the discovery that the AHE is linked to the summation of Ωn(k) over all the occupied bands below EF21.
The Ωn(k) is a local gauge field associated with the Berry phase of the band structure and determines the topological aspects of a material. In contrast to previous understanding, it is possible to control the Berry curvature and thus the intrinsic AHE and ANE by suitable manipulations of symmetries and band structures, independent of the finite value of the magnetization. As a result of these considerations, the AHE and ANE have recently been tuned in a distinct manner by tailoring the distribution of Ωn(k) in topological matter, such as in Dirac metals or chiral antiferromagnets5,6,7,8,9,22,23,24,25,26. These investigations have led to the observation of an AHE and an ANE in the absence of ferromagnetism. Furthermore, it has been demonstrated that by manipulating the crystal and magnetic space group symmetry and details of the band structure, the anomalous Hall conductivity can be tuned from zero to a large value27. The Berry curvature-driven anomalous Hall and Nernst effects have been measured in the noncollinear antiferromagnets Mn3Sn and Mn3Ge without sizeable magnetization, where Berry curvature effects are generated from the noncollinear spin structure9,22,23,24,25. A large enhancement in ANE has been observed in ultrathin films of ferromagnetic metal, including Fe, Co, Ni, and Ni80Fe20 due to intrinsic effects and skew scattering through spin-orbit coupling28. Additionally, in the Dirac semimetal Cd3As2, the AHE and ANE were measured due to Berry curvature effects produced by the separation of the Weyl nodes in a magnetic field7,8. The results of both experiments clearly fall outside the scope of the conventional model that scales the ANE with the magnetization of the system, but a worthy question remains. Is it possible to push the limit of ANE beyond the magnetization scaling relation in a ferromagnet? Hence, this work desires to go beyond the recent experiments, identify a material with a large Ωn(k) at EF and perform Nernst measurements on this system.
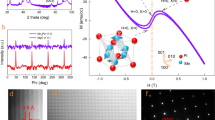
In the present study, we carried out thermoelectric experiments on the ferromagnetic topological Heusler compound Co2MnGa, which has previously been shown to exhibit a large AHE and a large Berry curvature distribution around EF27,29. Co2MnGa is a full Heusler compound that crystallizes in the L21 structure with space group Fm\(\bar 3\)m and a lattice constant a = 5.77 Å (Fig. 1(a)). The structure consists of four interpenetrating fcc sublattices, of which two are formed by Co atoms. The other two sublattices are formed by the Mn and Ga atoms. The structure can also be implicitly viewed as a zinc-blende-type sublattice, formed by one Co and Ga in which tetrahedral and octahedral holes are occupied by the second Co and Mn atom, respectively. The Co atoms occupy the Wyckoff position 8c (1/4,1/4,1/4), whereas the Mn and Ga atoms occupy the Wyckoff positions 4a (0, 0, 0) and 4b (1/2,1/2,1/2), respectively. Without spin-orbit coupling, there are three nodal lines near EF (Fig. 1(b), (c)). The spin-orbit coupling lifts the degeneracy in these lines by breaking mirror symmetry depending on the magnetization direction, and a small gap develops (Fig. 1(c) and Fig. S8). The gapping out of nodal lines induces a nonzero Ωn(k) into the system, which makes Co2MnGa a promising candidate for the study of Berry curvature related effects. A recent angle-resolved photoemission spectroscopy (ARPES) study in a Co2MnGa single-crystal shows the position of the nodal lines close to the Fermi level30.
a Crystal structure of Co2MnGa. The structure consists of four interpenetrating fcc sublattices. Two of the sublattices are formed by Co atoms, and the other two are formed by Mn and Ga atoms. b Electronic structure of Co2MnGa with and without spin-orbit coupling (SOC). The nodal line regions are marked with circles and magnified in the inset. SOC induces a gap in the nodal line in the blue colored circle by lifting the degeneracy of the bands. The dashed lines indicate different positions of the Fermi level (EF) with respect to the charge neutrality point E0. c Berry curvature distribution in Brillouin zone with [01\(\bar 1\)] magnetization direction. The dotted green lines indicate the nodal lines. The Berry curvature is concentrated around the gapped lines. d Schematic representation of the Nernst measurement. In this geometry, a transverse thermoelectric voltage Vy is produced by a temperature gradient ∇Tx and a magnetic field μ0H normal to each other
Materials and methods
Co2MnGa single-crystal growth
Single crystals of Co2MnGa were grown using the Bridgman–Stockbarger crystal growth technique. For growing a single-crystal, we first synthesized a polycrystalline sample by induction melting from the high-quality stoichiometric amounts of elemental cobalt (99.999%), manganese (99.999%), and gallium (99.999%) in an alumina crucible. The induction-melted sample was then crushed into powder form and packed in a custom-designed sharp-edged alumina tube that was sealed in a tantalum tube. The sample was heated to 1523 K and soaked for 10 h to ensure homogeneity of the melt and then slowly cooled to 1023 K. The crystallinity of the as-grown crystal was checked by white-beam backscattering Laue X-ray diffraction at room temperature. The aligned crystal was cut into bar-shaped samples for transport and magnetization measurements. The typical dimension of the crystals used for electrical and thermal transport measurements was 7.5 × 2 × 0.5 mm3.
Magnetization and electrical transport measurement
Magnetization measurements were performed using a Quantum Design vibrating sample magnetometer (MPMS). The electrical transport properties were measured in a Quantum Design physical property measurement system (PPMS, ACT option). The standard four-probe method was used for electrical transport measurement. To correct for contact misalignment, the measured raw data were field symmetrized and antisymmetrized.
Thermoelectric transport measurements
The zero-field temperature-dependent Seebeck coefficient was measured by the one-heater and two-thermometer configuration using the thermal transport option (TTO) of the PPMS (Quantum Design). Thermal conductivity measurements were performed in PPMS using the TTO option. Magneto-Seebeck and Nernst thermoelectric measurements were carried out using a one-heater and two-thermometer configuration on a PPMS. The instrument was controlled by software programmed using LabVIEW. The measurement was performed in the temperature range of 60–340 K, and magnetic fields were swept in both directions. The temperature gradient was generated using a resistive heater connected to the gold-coated copper plate at one end of the sample. The thermal gradient, ∇T, was applied along the [111] direction of the sample, and a magnetic field was applied along the [01\(\bar 1\)] direction. For the heat sink, a gold-plated copper plate was attached to the puck clamp. To measure the temperature difference, two gold-plated copper leads were attached directly to the sample using silver epoxy along the thermal gradient direction. The distance between the thermometers was ~4 mm. The ∇T was typically set to 1−3% of the sample temperature. The transverse voltage due to the thermal gradient was measured by attaching two copper wires orthogonal to the heat gradient direction of the sample using silver epoxy. The Seebeck thermopower was estimated using the relation Sxx = Vx/∇Tx, where Vx is the longitudinal voltage. The Nernst thermopower was estimated as Syx = LxVy/(Ly∇Tx), where Vy is the transverse voltage, Lx is the distance between two temperature leads, and Ly is the distance between two voltage wires.
Nernst data survey
We reproduced the magnetization-dependent anomalous Nernst thermopower value for different ferromagnets well below their Curie temperatures from a previous report by Ikhlas et al.9. Specifically, Mn3Sn (200 K; ref. 9.), Fe3O4 (300 K, B < 0.8 T; ref. 20.), Co/Ni films (300 K; ref. 31.), L10-FePt (300 K; ref. 31.), D022-Mn2Ga (300 K; ref. 31.), L10-MnGa (300 K; ref. 31.), L10-FePd (300 K; ref. 31.), Nd2Mo2O7 (T < Tc = 73 K, B = 1 T [111]; ref. 32.), Fe (300 K; ref. 33.), Co (300 K; ref. 33.), MnGe (140 K, B > 2 T; ref. 34.), MnGe (100 K, B > 5 T; ref. 34.), MnGe (20 K, B < 14 T; ref. 34) and Pt/Fe multilayer with N = 1–9 (300 K, B < 5 T; ref. 35) were reproduced.
Ab initio calculations
For our ab initio calculations, we employed density-functional theory (DFT) using VASP36. The exchange-correlation energy is described via PBE. For integrations in k-space, we used a grid of 19 × 19 × 19 points. We extracted Wannier functions from the resulting band structure using WANNIER9037 to set up a tight-binding Hamiltonian, which reproduced the DFT band structure within a few meV. With this Hamiltonian, we calculated the Berry curvature \({\vec{\mathrm \Omega }}_n\) via:
where m and n are the eigenstates and ε are the eigenenergies of the Hamiltonian H.
The anomalous Hall conductivity \((\sigma _{xy}^A)\) was calculated using the equation5:
where fnk is the Fermi-Dirac distribution function with the band index n and the wave vector k. Parameter e denotes the elementary charge and \(\hbar\) is the reduced Planck constant. The integral was performed across the whole Brillouin zone for all bands below EF. The anomlous Nernst conductivity (\(\alpha _{yx}^A\)) was calculed as5:
where εnk is the band energy, kB is the Boltzmann constant and β = kBT.
To realize integrations over the whole Brillouin zone for AHE and ANE, we employed a mesh of 251 × 251 × 251 k-points, and this mesh was carefully checked to ensure convergence.
Results and discussion
The single crystals used in this study were synthesized via the Bridgman–Stockbarger crystal growth technique. Prior to the transport experiments, the as-grown crystals were characterized by Laue X-ray diffraction (XRD), where sharp spots in the pattern indicate high crystal quality (see Materials and methods for details, Supplementary Fig. S1). The transport experiments were performed in a temperature-variable cryostat (Physical Property Measurement System from Quantum Design) in a helium atmosphere equipped with a 9 T magnet. All transport experiments were performed within the [111] plane of the Co2MnGa crystal with a magnetic field μ0H applied in the [01\(\bar 1\)] direction. In particular, two measurement configurations were used in our study. First, longitudinal measurements were done, where the electric voltage response was measured in the direction of the applied electrical current (I) or heat current (Q) (the corresponding transport parameters are marked with the subindex xx). Second, transverse measurements were done, where the electric voltage response was measured normal to the applied electrical current or temperature gradient (the corresponding transport parameters are marked with the subindex yx, Fig. 1(d)). To gain deeper insights into the experimental results, ab initio calculations were performed using density-functional theory as implemented in VASP36 as a first step, followed by the extraction of a Wannier tight-binding Hamiltonian via WANNIER9037. With this Hamiltonian, we can evaluate the Berry curvature and consecutively evaluate the AHE and ANE (for further details, see the Materials and methods section).
In the first set of transport experiments, we investigated the longitudinal thermoelectric magneto-transport of Co2MnGa. Figure 2(a) shows the electrical resistivity (ρxx) and Seebeck coefficient (Sxx) as a function of temperature T. The decreasing ρxx with decreasing T reveals the metallic behavior of the compound with a value of 130 μΩ cm at 300 K. The temperature-dependent Seebeck coefficient (Sxx) for Co2MnGa shows a negative sign throughout the measurement temperature. This observation indicates electron-dominated transport in the thermoelectric signal. Furthermore, the magnitude of Sxx increases with increasing T and reaches a value of approximately −26 μV K−1 at 300 K. We would like to note that the temperature-dependent Sxx does not show any suppression at high temperatures. This lack of suppression is a clear indication of the absence of a bipolar effect in the system (Supplementary discussion, Figs. 2a and S2). The magneto-Seebeck data show almost no field-dependence of Sxx within the measured temperature range (Supplementary Fig. S3).
a Temperature (T)-dependent electrical resistivity (ρxx) and zero-field Seebeck coefficient (Sxx). Electrical (I) and heat current (Q) have been applied along the [111] direction of the crystal. b Magnetic field-dependence of the magnetization (M) at different T. c Magnetic field-dependence of the Hall conductivity (σxy). The Hall conductivity was extracted by employing the measured off-diagonal (ρyx) and diagonal components (ρxx) of the resistivity tensor. The inset shows the temperature dependence of the anomalous Hall conductivity \(( {\sigma _{xy}^A} )\). d Theoretically estimated Hall conductivity as a function of chemical potential at T = 0 K for Co2MnGa. The dashed lines indicate different positions of the Fermi level (EF) with respect to the charge neutrality point E0
Next, we measured the magnetization (M) of our sample. The compound is known to be a ferromagnet with a relatively high Curie temperature of (TC = 687 K)38. In Fig. 2(b), we present temperature-dependent magnetization data for Co2MnGa. In agreement with the literature, we observed ferromagnetic behavior. From the data taken as a function of the sweeping magnetic field, a saturation magnetization value of approximately Msat = 3.9 μB f.u.−1 was measured at 50 K, which slightly decreased with increasing temperature to Msat = 3.7 μB f.u.−1 at 300 K.
Furthermore, we measured the anomalous Hall effect of Co2MnGa. We estimated the total Hall conductivity (σxy) from the measured Hall resistivity ρyx and the longitudinal resistivity ρxx as:
In Fig. 2(c), we present σxy as a function of the magnetic field at different base temperatures. As expected for a ferromagnetic material, σxy increases with μ0H and saturates when the saturation magnetization is reached despite a small slope contributed by the ordinary Hall effect (compare with Fig. 2(b)). The anomalous Hall conductivity (AHC) \(( {\sigma _{xy}^A} )\) was estimated by extrapolating the slope of the high-field data points (Supplementary Fig. S4) to the zero-field value. The observed values of \(\sigma _{xy}^A\) and its temperature dependence are consistent with previous reports27. As shown in the inset of Fig. 2(c), a value of \(\sigma _{xy}^A\)~ 1260 S cm−1 was estimated at 60 K and gradually decreases with increasing temperature and reaches ~845 S cm−1 at 300 K. From the magnetic field-dependence, one would naively expect \(\sigma _{xy}^A\) to only scale with M. However, as shown in our ab initio calculation in Fig. 2(d), the AHC conductivity in Co2MnGa strongly depends on the position of the Fermi level, which is due to the Berry curvature effect discussed above. In the case of the intrinsic AHE, Ωn(k) adds a term to the group velocity of the electron5 (see Eq. 2, Materials and methods).
Recent results of ARPES measurements on our sample show that the actual Fermi level EF in our sample is slightly shifted toward the valence bands compared to that of the theoretical charge neutral point E0, which is estimated by counting the intrinsic electron number by EF – E0 = −80 meV30. Based on the ab initio calculations and ARPES results, we predicted an AHC value of \(\sigma _{xy}^A\left( {E_{\mathrm{F}}} \right) =\)1242 S cm−1 at T = 0 K. Extrapolating the measured \(\sigma _{xy}^A\) linear to T = 0 K, we obtained a value of \(\sigma _{xy}^A\) = 1362 S cm−1, which is reasonably close to the experimentally measured value.
Next, we investigated the Nernst effect of Co2MnGa. In Fig. 3(a) (also see Supplementary Fig. S5), the field-dependence of the Nernst thermopower (Syx) is shown at different T. At all T, the Nernst signal increases rapidly at low magnetic fields (μ0H) and saturates above μ0H ~ 1 T despite a small remaining increase due to ordinary Nernst signal contribution. These features are consistent with the M and \(\sigma _{xy}^A\) data. We, therefore, attribute the saturation value of the Nernst signal to the ANE and the small increasing contribution beyond 1 T to the ordinary Nernst effect. In a similar procedure as that for the Hall data, the ordinary and anomalous contributions to the Nernst thermopower can then be separated by fitting the high-field slope of the total Nernst thermopower up to μ0H = 9 T (Supplementary Fig. S4). In doing so, we found that the ordinary Nernst effect reached values of \(S_{yx}^O\)= 50 nV K−1 at room temperature and μ0H = 1 T. The ANE, on the other hand, reached remarkably high values of \(S_{yx}^A\) ~6.0 µV K−1 at 300 K (inset of Fig. 3(a)), for example. Similar to the AHE, the ANE of conventional ferromagnets is proportional to the magnetization, that is, |\(S_{yx}^A\)|=|\(N_{yx}^A\)|μ0M, where |\(N_{yx}^A\)|is the anomalous Nernst coefficient, ranging from 0.05 to 1 μV K−1T −1 at 300 K. According to this relation, Co2MnGa should maximally exhibit \(S_{yx}^A\) = 0.9 µV K−1 (see Materials and methods for details). This value is ~7 times lower than that observed in the experiment and indicates that the ANE arises from a mechanism that is distinct from the linear scaling of conventional ferromagnets. We also plotted the temperature (T) normalized Nernst effect (Syx/T) at different temperatures for the Co2MnGa samples. The anomalous Nernst amplitude shows nearly T-independent behavior at high temperatures (Supplementary Fig. S6).
a Magnetic field-dependence of the Nernst thermopower (Syx) of Co2MnGa at different temperatures T. The inset shows the extracted anomalous Nernst thermopower (\(S_{yx}^A\)) extrapolating the slope of the high-field (above 1 T) data points as a function of T. b Magnetic field-dependence of the transverse thermoelectric conductivity (αyx) at different T. c Theoretically calculated anomalous Nernst conductivity (\(\alpha _{yx}^A\)) as a function of the chemical potential with respect to the charge neutrality point E0 at T = 300 K for Co2MnGa. The dashed lines indicate different positions of the Fermi level EF. d T-dependence of the experimentally determined \(\alpha _{yx}^A\). The inset of the plot shows the theoretically estimated temperature dependence of \(\alpha _{yx}^A\) at the Fermi level positions marked in c
In the Nernst effect and thermal conductivity, the electron and hole contributions toward the total transport are additive in nature. Therefore, to understand the multicarrier or bipolar effect in the system, we performed temperature-dependent thermal conductivity measurements of Co2MnGa up to room temperature. The analysis of thermal conductivity data shows that the κlat at high temperatures follows the T−1 relationship (for details, see Supplementary Fig. S7 and discussion). Hence, the temperature-dependent Seebeck coefficient (discussed above and in Supplementary information) and thermal conductivity data provide important experimental evidence to exclude the multicarrier effect and, therefore, verify the role of topological effects for the large anomalous Nernst signal in Co2MnGa.
To gain deeper insight into the large ANE in Co2MnGa, we calculated the transverse thermoelectric conductivity (αyx) plotted in Fig. 3(b)). Using the measured components of ρxx, ρyx, Sxx, and Syx, we estimated αyx via:
Based on the linear scaling relation for conventional ferromagnetic metals, one would expect that αyx increases linearly with decreasing T and follows the temperature dependence of M17. However, in Co2MnGa, we observed the inverse effect, whereby \(\alpha _{yx}^A\) increased with increasing temperature, although the saturation magnetization decreased. This outcome is another indication that the anomalous Nernst signal in ferromagnetic Co2MnGa arises from a different mechanism than the ANE in conventional ferromagnets. It is noteworthy that the AHC in Co2MnGa also does not follow the conventional scaling relation. In topological ferromagnetic metals, the anomalous signal is purely intrinsic, is universal and arises due to the Berry curvature [Ωn(k)] effect rather than the magnetization of the material21. These characteristics suggest that the ANE and the AHE in Co2MnGa may share a common origin, which is the Berry curvature effect.
To evaluate this possibility, we calculated \(\alpha _{yx}^A\), employing Eq. 35 (see Materials and methods). The {(εnk − μ)fnk + kBT ln [1 + e−β(εnk − μ)]} term has finite values only around the Fermi energy. Therefore, while \(\sigma _{xy}^A\) is related to the summation of Ωn(k) of all the occupied bands below EF, \(\alpha _{yx}^A\) is related to Ωn(k) of all bands near EF. As discussed earlier, the Fermi level is ~ − 80 meV shifted from neutral point E0, which provided access to all three nodal lines. Thus, a suitable position of EF results in a strong Berry curvature effect in Co2MnGa. Our theoretical calculations show a very large ANC in the system, which is linked to the high Berry curvature induced by the gapping of the nodal lines (Fig. 3(c)). Like the AHC, the ANC shows a strong Fermi level dependence, which is not captured by the conventional theory for ferromagnets. As the suitable position of the Fermi level is important to observe the Berry curvature effect in anomalous transport, it would be interesting to explore the anomalous signal by tuning the Fermi level position by doping.
Importantly, the calculations reproduced and explained the T-dependence of the experimental data, as shown in the inset of Fig. 3(d). At EF – E0 = −80 meV, the Berry curvature in the model led to the same characteristic decrease of \(\alpha _{yx}^A\) with decreasing T that was also observed in the experiment. We note that only slight shifts in the position of EF leads to a strong modification of the T-dependence of \(\alpha _{yx}^A\). Thus, \(\alpha _{yx}^A(T)\) is a sensitive probe for the underlying mechanism for the ANE in Co2MnGa. The coincident observation of the high values of AHE and ANE, together with the same characteristic T-dependence of \(\alpha _{yx}^A\) in experiment and theory, go beyond the conventional model for the ANE in ferromagnets and can be considered as fingerprints of the Berry curvature effect associated with emerging nodal lines and Weyl points.
Finally, we turn to the initial question of whether the value of the ANE in such topological ferromagnets can exceed the highest values observed in conventional ferromagnets. Therefore, in Fig. 4, the anomalous Nernst signal of Co2MnGa is compared with the values of various other ferromagnetic metals9,20,31,32,33,34,35, extending the plot of Ikhlas et al.9. We plotted the absolute values of the Nernst thermopower in the magnetically ordered states, where μ0H and T were kept as absolute parameters. The shaded area of the graph represents the linear relation of the anomalous Nernst thermopower as measured for conventional ferromagnets. The red dotted line marks the limit of the highest value of |\(S_{yx}^A\)| ever measured in a ferromagnet. As explained above, according to the conventional scaling relation, the expected value of \(S_{yx}^A\) for Co2MnGa at room temperature is ~0.05 to 0.9 µV K−1. Nevertheless, the Nernst signal of Co2MnGa shows a much larger value ∼6.0 µV K−1 at room temperature and further increased to ~6.6 µV K−1 at 340 K.
Comparison of the magnetization-dependent anomalous Nernst thermopower (|\(S_{yx}^A\)|) of various ferromagnetic metals (see Materials and methods for details), chiral antiferromagnet Mn3Sn and Co2MnGa extending the plot of Ikhlas et al.9. The shaded region indicates the linear relation for conventional ferromagnetic metals |\(S_{yx}^A\)| = |\(N_{yx}^A\)|µ0M, with |\(N_{yx}^A\)| ranging from ∼0.05 µV K−1 T−1 to ∼1 µV K−1 T−1. The red dotted line indicates the upper limit of the measured value of |\(S_{yx}^A\)| in a conventional ferromagnet. The Nernst signal for Co2MnGa falls out of the scope of this relation, similar to Mn3Sn. The |\(S_{yx}^A\)| for Co2MnGa shows the largest value reported among ferromagnetic metals at room temperature
Conclusions
In summary, we have observed a remarkably large ANE in the ferromagnetic topological Heusler compound Co2MnGa, which is ~7 times larger than any value reported for conventional ferromagnets to date in the literature. Combined electrical, thermoelectric and first-principles calculations revealed that this high value of the ANE arises from a large net Berry curvature near the Fermi energy associated with nodal lines and Weyl points. Our results show that the ANE in Co2MnGa originates from a net Berry curvature of all bands near EF rather than directly from the magnetization. The large Nernst signal at room temperature and high Curie temperature also make Co2MnGa an ideal candidate for further investigation for use in transverse thermoelectric devices. Moreover, it would be interesting to explore the anomalous signal by tuning the Fermi level position by doping. In a broader sense, the flexible electronic structure of Heusler compounds can open up adequate room for the realization of a giant Nernst effect via a suitable Berry curvature design. We believe that the present study can act as a guide in the search for new magnetic topologically nontrivial materials with a large nonzero Berry curvature for the observation of a giant anomalous Nernst effect.
Note added to proof
During the peer review process of our paper, we noticed that another independent group also found a large anomalous Nernst effect in Co2MnGa39.
References
Rowe, D. M. CRC Handbook of Thermoelectrics. CRC Handbook of Thermoelectrics. (CRC Press, Boca Raton, FL, 1995).
Nolas, G. S., Sharp, J. & Goldsmid, J. Thermoelectrics: Basic Principles and New Materials Developments, Springer series in materials science Vol. 45, Chapter 1 (Springer Science & Business Media, 2013).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Pu, Y., Chiba, D., Matsukura, F., Ohno, H. & Shi, J. Mott relation for anomalous Hall and Nernst effects in Ga1-xMnxAs ferromagnetic semiconductors. Phys. Rev. Lett. 101, 117208 (2008).
Xiao, D., Yao, Y., Fang, Z. & Niu, Q. Berry-phase effect in anomalous thermoelectric transport. Phys. Rev. Lett. 97, 026603 (2006).
Xiao, D., Chang, M. C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Liang, T. et al. Anomalous Nernst effect in the dirac semimetal Cd3As2. Phys. Rev. Lett. 118, 136601 (2017).
Jia, Z. et al. Thermoelectric signature of the chiral anomaly in Cd3As2. Nat. Commun. 7, 13013 (2016).
Ikhlas, M. et al. Large anomalous Nernst effect at room temperature in a chiral antiferromagnet. Nat. Phys. 13, 1085–1090 (2017).
Thierschmann, H. et al. Three-terminal energy harvester with coupled quantum dots. Nat. Nanotechnol. 10, 854–858 (2015).
Bergenfeldt, C., Samuelsson, P., Sothmann, B., Flindt, C. & Büttiker, M. Hybrid microwave-cavity heat engine. Phys. Rev. Lett. 112, 76803 (2014).
Sánchez, D. & Serra, L. Thermoelectric transport of mesoscopic conductors coupled to voltage and thermal probes. Phys. Rev. B 84, 201307 (2011).
Entin-Wohlman, O., Imry, Y. & Aharony, A. Three-terminal thermoelectric transport through a molecular junction. Phys. Rev. B 82, 115314 (2010).
Behnia, K. & Aubin, H. Nernst effect in metals and superconductors: a review of concepts and experiments. Rep. Prog. Phys. 79, 046502 (2016).
Behnia, K. The Nernst effect and the boundaries of the Fermi liquid picture. J. Phys. Condens. Matter 21, 113101 (2009).
Watzman, S. J. et al. Dirac dispersion generates large Nernst effect in Weyl semimetals. Phys. Rev. B 97, 161404 (2018).
Miyasato, T. et al. Crossover behavior of the anomalous Hall effect and anomalous nernst effect in itinerant ferromagnets. Phys. Rev. Lett. 99, 086602 (2007).
Lee, W. L., Watauchi, S., Miller, V. L., Cava, R. J. & Ong, N. P. Anomalous Hall heat current and Nernst effect in the CuCr2Se4- xBrx ferromagnet. Phys. Rev. Lett. 93, 226601 (2004).
Smith, W. A. The transverse thermomagnetic effect in nickel and cobalt. Phys. Rev. 33, 295–306 (1911).
Ramos, R. et al. Anomalous Nernst effect of Fe3O4 single crystal. Phys. Rev. B 90, 054422 (2014).
Burkov, A. A. Anomalous Hall effect in Weyl metals. Phys. Rev. Lett. 113, 187202 (2014).
Nayak, A. K. et al. Large anomalous Hall effect driven by a nonvanishing Berry curvature in the noncolinear antiferromagnet Mn3Ge. Sci. Adv. 2, e1501870–e1501870 (2016).
Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212–215 (2015).
Li, X. et al. Anomalous Nernst and righi-leduc effects in Mn3Sn: berry curvature and entropy flow. Phys. Rev. Lett. 119, 056601 (2017).
Kiyohara, N., Tomita, T. & Nakatsuji, S. Giant anomalous Hall effect in the chiral antiferromagnet Mn3Ge. Phys. Rev. Appl. 5, 064009 (2016).
Chang, G. et al. Room-temperature magnetic topological Weyl fermion and nodal line semimetal states in half-metallic Heusler Co2TiX (X=Si, Ge, or Sn). Sci. Rep. 6, 38839 (2016).
Manna, K. et al. From colossal to zero: Controlling the anomalous hall effect in magnetic Heusler compounds via berry curvature design. Phys. Rev. X 8, 041045 (2018).
Chuang, T. C., Su, P. L., Wu, P. H. & Huang, S. Y. Enhancement of the anomalous Nernst effect in ferromagnetic thin films. Phys. Rev. B 96, 174406 (2017).
Kübler, J. & Felser, C. Weyl points in the ferromagnetic Heusler compound Co2MnAl. EPL 114, 47005 (2016).
Belopolski, I. et al. A three-dimensional magnetic topological phase. arXiv 1712, 09992 (2017).
Hasegawa, K. et al. Material dependence of anomalous Nernst effect in perpendicularly magnetized ordered-alloy thin films. Appl. Phys. Lett. 106, 252405 (2015).
Hanasaki, N. et al. Anomalous Nernst effects in pyrochlore molybdates with spin chirality. Phys. Rev. Lett. 100, 106601 (2008).
Weischenberg, J., Freimuth, F., Blügel, S. & Mokrousov, Y. Scattering-independent anomalous Nernst effect in ferromagnets. Phys. Rev. B 87, 060406 (2013).
Shiomi, Y., Kanazawa, N., Shibata, K., Onose, Y. & Tokura, Y. Topological Nernst effect in a three-dimensional skyrmion-lattice phase. Phys. Rev. B 88, 064409 (2013).
Uchida, K. I. et al. Enhancement of anomalous Nernst effects in metallic multilayers free from proximity-induced magnetism. Phys. Rev. B 92, 094414 (2015).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Mostofi, A. A. et al. wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Ido, H. & Yasuda, S. Magnetic properties of Co-Heusler and related mixed alloys. Le. J. Phys. Colloq. 49, C8–141 (1988).
Sakai, A. et al. Giant anomalous Nernst effect and quantum-critical scaling in a ferromagnetic semimetal. Nat. Phys. 14, 1119–1124 (2018).
Acknowledgements
This work was financially supported by the ERC Advanced Grant No. 742068 “TOP-MAT”, and Deutsche Forschungsgemeinschaft DFG under SFB 1143. S.N.G. and Ch.F. acknowledges financial support from the Alexander von Humboldt Foundation.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Guin, S.N., Manna, K., Noky, J. et al. Anomalous Nernst effect beyond the magnetization scaling relation in the ferromagnetic Heusler compound Co2MnGa. NPG Asia Mater 11, 16 (2019). https://doi.org/10.1038/s41427-019-0116-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-019-0116-z
This article is cited by
-
Creation of flexible spin-caloritronic material with giant transverse thermoelectric conversion by nanostructure engineering
Nature Communications (2024)
-
Anisotropic anomalous Nernst effect of metallic nickel assembled by aligned nanowires
Journal of Materials Science (2024)
-
Anomalous Nernst effect in the topological and magnetic material MnBi4Te7
npj Quantum Materials (2023)
-
Large anomalous Hall effect and negative magnetoresistance in half-topological semimetals
Communications Physics (2023)
-
Anisotropic resistance with a 90° twist in a ferromagnetic Weyl semimetal, Co2MnGa
Nature Communications (2023)