Abstract
Metal-to-insulator transition (MIT) behaviors accompanied by a rapid reversible phase transition in vanadium dioxide (VO2) have gained substantial attention for investigations into various potential applications and obtaining good materials to study strongly correlated electronic behaviors in transition metal oxides (TMOs). Although its phase-transition mechanism is still controversial, during the past few decades, people have made great efforts in understanding the MIT mechanism, which could also benefit the investigation of MIT modulation. This review summarizes the recent progress in the phase-transition mechanism and modulation of VO2 materials. A representative understanding on the phase-transition mechanism, such as the lattice distortion and electron correlations, are discussed. Based on the research of the phase-transition mechanism, modulation methods, such as element doping, electric field (current and gating), and tensile/compression strain, as well as employing lasers, are summarized for comparison. Finally, discussions on future trends and perspectives are also provided. This review gives a comprehensive understanding of the mechanism of MIT behaviors and the phase-transition modulations.
Similar content being viewed by others
Introduction
In the past decades, the elucidation of the physical properties of strongly correlated systems has been one of the most challenging subjects in condensed matter physics and has continued to pose controversial theoretical, as well as experimental, issues. As such, the V–O system could be one of the most attractive materials, which is characteristic of a great variety of compounds, such as VO, V2O3, V3O5, V4O7, V5O9, V6O11, V7O13, V8O15, VO2, V2O5, etc1,2. Many of them exhibit a typical metal-to-insulator phase transition (MIT) with sharp changes in optical, electrical, thermal, and magnetic properties3,4,5,6,7,8,9. Such a system not only yields wide application potential but also provides scientists with important and interesting materials to study the phase-transition mechanism. Vanadium dioxide (VO2) is the most interesting compound in the V–O system because its transition temperature is located just near room temperature. Although its phase-transition mechanism is still controversial, the modification of the phase transition has undergone considerable progress in recent years.
The MIT behavior in VO2 was first reported by Morin in 195910. The first-order monoclinic (M) insulator phase to rutile (R) metallic phase transition in VO2 is accompanied by a large and rapid change in the electrical and optical properties, with potential traditional applications in switching and sensing, as well as the modulation of infrared (IR) wavelengths11,12,13,14. Recently, VO2 has received renewed attention as a convenient strongly correlated material with the advent of new ultrafast and microscopy techniques15,16,17,18, ionic gating19,20, and improved computational approaches21. Based on those new research tools, people have made great efforts in many research aspects, such as material morphologies (films, nanobelts, nanowires (NWs), etc.), fabrication methods, phase-transition mechanisms, and the modulation of MIT behaviors. Several studies have reported on different VO2 morphologies using various fabrication methods and accompanied by performance improvement22,23. Additionally, a deep understanding of the mechanisms behind phase-transition behaviors is beneficial to better modulating performance in VO2 materials. Meanwhile, the modulation of the VO2 phase transition can not only directly affect the performance of the material and broaden its applications but also help to understand the phase-transition mechanism. However, until now, few reports have focused on a summary of the fundamental mechanism and modulation of the phase transition in VO2.
As a classical transition metal oxide (TMO), VO2 behaves insulating abnormally near room temperature with a 3d1 electronic structure that cannot be explained by traditional band theory. Additionally, in the IMT process, many other insulating phases appear under certain stress and temperature conditions24,25, which result in difficulties in understanding the specific changes in the electronic and crystallographic structures. Based on these phenomena and observations, a structure-driven Peierls transition mechanism or electron correlation mechanism could be responsible for the narrowing of the band gap and collapse of lattice symmetry. To clarify which of those two models, if either, yields an appropriate description of VO2, many theoretical and experimental studies have been performed, one of which even explicitly asked “VO2: Peierls or Mott–Hubbard?” in its title26. Later, with the development of observation and characterization techniques, an instantaneous metal-like monoclinic phase was discovered during the transition, which means a certain coincidence of the crystallographic phase transition (CPT) and the insulator-to-metal transition (IMT)27. Moreover, the orbital occupancy and shift could be directly connected both with the delocalization of electrons and the lattice distortion28. Therefore, the study of the interactions among the electrons, orbitals, and lattice structure has been the focus of the peculiar transition in VO2, which could also provide constructive guidance in the modulation of the transition character. For the modulation of the phase transition in VO2, traditional methods consist of doping29,30,31 or using an external excitation (electric current, strain, etc.)15,32,33, which could be attributed to the regulation of the internal factors. Facts have proven that these interaction-based modulations could be effective and operable; however, one is still faced with a series of matters, such as irreversibility, noncontinuity, heat triggering, etc. The new modulations, which are expected to achieve manual and dynamic control of the transition, are different from the previous passive control. For example, in the past, Joule-heating-based electric current modulation was hard to operate, but now, static electric gating based on controlling the internal defects provides good control of the phase transition or even stabilizes the metallic phase19. In this review, we will summarize the recent progress in the understanding of the phase-transition mechanism and modulation methods of the phase transition. Compared to former reviews, a comprehensive, updated and critical discussion of different explanations of the phase-transition mechanism, as well as novel modulation and investigation methods, will be given. This work presents a clear picture of the recent progress in understanding the mechanism of MIT behaviors and the phase-transition modulations of VO2 materials.
Understanding of the VO2 phase-transition mechanism crystal structure of VO2
VO2 can exhibit many different structures with different growth conditions, in which the M1 and R phase are the most common ones due to the reversible transition near room temperature, as shown in Fig. 1. Figure 2a is the crystal structure of VO2 (R) with a space group of P42/mnm (No. 136), cell parameters: a = b = 0.455 nm, c = 0.286 nm. In the VO2 (R) crystal structure, the V4+ ions occupy the body center and the vertex of the tetragonal structure, and each V4+ ion and six surrounding O2− ions constitute an octahedral VO6 unit. In the z-axis direction, the distance between the nearest V–V atoms is equal to 0.287 nm. Figure 2b is the crystal structure of VO2 (M) with space group P21/c (No.14), unit cell parameters: a = 0.575 nm, b = 0.452 nm, c = 0.538 nm, β = 122.6°34. When the phase transition occurs, the crystal parameters change, and the V atom deviates from the vertex angle. The highly symmetrical quadrilateral structure becomes a monoclinic structure of low symmetry, and two varying length V–V bonds are formed. The long distance is 0.312 nm, and the short spacing is 0.265 nm. The d-electrons of each V atom are bound to these V–V bonds, revealing the localization that leads VO2 to show the insulative property. It has been suggested that such a V–V dimer formation directly leads to the change from the high-temperature delocalized state to the localized state.
a The monoclinic insulator and b the rutile metal124. Copyright© 2015 Elsevier Ltd
In 1949, Mott predicted the MIT characteristics of VO2 by band theory35. Mott predicted that its energy band structure changed at the same time as the MIT phase transition. The bottom of Fig. 2 shows the high-temperature rutile phase and low-temperature Monoclinic band structure. In the rutile phase band structure, the Fermi level falls between the π* band and the d// band, which shows the electric conductivity of a metal. In the monoclinic band structure, the d// band is split into two energy bands (d// band and d//* band), and a forbidden band is formed between the d// band and the π* band. The forbidden bandwidth is approximately 0.7 eV, and the Fermi level falls within the forbidden band, which makes VO2 insulative.
However, whether the lattice distortion causes the MIT has not yet been clarified. This problem has actually become the focus of VO2 materials research. The discovery of some peculiar phenomena proves that structural distortion is apparently not the only factor that causes the phase change of the metal/insulator, or even a necessary factor. The first phenomenon is the discovery of other phases at low temperatures. In addition to the M1 phase, with the use of elemental (Cr) doping or stress effects, people also found the presence of the M2 phase. By using micro-Raman spectroscopy, Joanna et al.36 resolved the monoclinic VO2 (M1 and M2), stable rutile phase VO2 (R), triclinic VO2 (T) induced by temperature or strain. As shown in Fig. 3, in the M1 phase, the vanadium atoms are paired and tilted, forming zigzag chains along the cR axis. In contrast, the M2 phase has two distinct sublattices of V atoms: in sublattice A, the vanadium atoms are paired along the cR axis but not tilted, and in sublattice B, they are tilted perpendicular to the cR axis but unpaired. Furthermore, the T phase was found to be an intermediate phase. In addition, under the influence of external pressure, temperature, or electron injection, some metastable monoclinic metal phases are found, which means that even the dimerization of V–V atoms is unnecessary for the MIT37. The discovery of these new phases can no longer be explained by traditional lattice–electron interactions. Prior to this, electron–electron interactions were used to calculate and explain the occurrence of the VO2 phase transition. In the next section, we will explain the internal interaction of VO2 materials from the evolution of the phase-transition mechanism. On this basis, if we can artificially control this interaction, even a reversible continuous control, and then directly control the phase transition characteristics, it will greatly enhance the value of VO2 materials and also help to understand other TMOs.
a Strain–temperature phase diagram of the insulating phases of VO2 represented via the phonon frequency shift (ω0). b Positions of the vanadium atoms in the M1 (green) and M2 (dark gray, blue) phases. The triclinic phase is intermediate between these two states36. Copyright© 2012 the American Physical Society
Changes in the physical properties in VO2
In the VO2 system, the coupling of lattice, charge, spin, and orbital makes the VO2 produce abnormal physical phenomena in optical, electric, thermal, and other properties near the phase-transition point.
As shown in Fig. 1, high-quality VO2 single-crystalline films have a resistance change of 3–5 orders of magnitude. Additionally, the phase-transition points of the heating and cooling processes do not coincide with each other, as characterized by a certain thermal hysteresis. Such a sharp transformation from insulator to metal make VO2 widely used in ultrafast switches. Furthermore, as a strongly correlated oxide, the temperature-dependent electrical properties would also influence the whole material system. For example, in 2010, the Harvard group34 constructed a multilayer capacitor with an HfO2/VO2/HfO2/n-Si-substrate stack structure, and the results showed that the temperature-dependent capacitance underwent an abrupt change, whereas there was no change in the reference HfO2/Si capacitor (Fig. 4a).
a The temperature dependence of the capacitance measured from the HfO2/VO2/HfO2/Si stack device. The inset shows the temperature dependence of the capacitance from the reference HfO2 (40 nm)/Si MOS capacitor34. Copyright© 2010 the American Physical Society. b Temperature dependence of the measured total thermal conductivity (κtot) and expected electronic thermal conductivity of a VO2 nanobeam46. Copyright© 2017 the American Association for the Advancement of Science
As to the optical property of VO2, the MIT is accompanied by a dramatic change in the IR region38,39,40. At temperatures below Tc, VO2 is in the monoclinic phase, in which the V atoms pair and open an energy gap of 0.6 eV, permitting high IR transmission41. At temperatures above Tc, VO2 is in the metallic phase, in which overlap between the Fermi level and the V 3d band eliminates the aforementioned band gap, causing the material to be highly reflective or opaque in the near-infrared (NIR) region. Moreover, the critical temperature can be adjusted to near-room temperature. The ability to modulate the NIR transparency makes VO2 a promising material for next-generation smart windows.
Additionally, there are many thermal properties in this material system42,43,44. In 2010, Oh et al.45 reported that the thermal conductivity increases by as much as 60% in the metallic phase, which is in good agreement with the expected electronic contribution to the thermal conductivity. In this case, the VO2 thin film behaves effectively as a thermal switch, as it drastically changes the total thermal conductivity over a narrow temperature range. However, recently, Wu’s team46 discovered an unusual low electronic thermal conductivity in VO2 at high temperatures. They reported a drastic breakdown of the Wiedemann–Franz law at high temperatures, with L smaller than L0 by nearly an order of magnitude, which could be ascribed to the strong correlation in VO2. Furthermore, the total thermal conductivity of VO2 was found to be nearly constant, ~6 W/mK, across the MIT (see Fig. 4b). Another interesting result is that the doped VO2 (WxV1−xO2, Cu-doped VO247) shows an abrupt increase around the MIT, which holds potential for thermal switching.
Although VO2 is of great importance from both technological and basic research perspectives, the bulk material usually has complicated domain structures that unfortunately obscure its fundamental properties and make it challenging to probe its intrinsic MIT behaviors. One intriguing way to overcome this difficulty is to fabricate nanoscale samples with a size smaller than the characteristic domain size, which considerably simplifies the domain structures and fascinatingly provides a model system to investigate their intrinsic properties. In 2011, Sun et al.23 used in situ variable-temperature IR spectroscopy to identify the size-dependent MIT. They suggested that the size-related defect density and scattering efficiency could be used to account for the novel size-dependent MIT behaviors. For the VO2 thin films, it has been demonstrated that the surface layer could even affect the whole thickness of a film due to the strong association19, though we hardly understand the details of this phenomenon. In these efforts, single-crystalline NWs can be superior to thin films in several aspects of basic and practical importance: the MIT in such a nanostructure is ultimately sharp and affects the electron transport of the entire device; they can be made a single domain21; and they have better conductivity due to the lack of grain boundaries and lower concentrations of defects48. Furthermore, compared with the bulk and thin-film samples, due to the single-dimensional and single-crystalline properties, NWs and nanobelts can induce spontaneous structural changes to relieve surface stress, and the nature of the V–V chains can be substantially easier to regulate. In 2009, Sohn et al.49 reported that the unique surface structure of single-crystalline VO2 NWs having a specific crystallographic orientation naturally induced Mott-insulating M2 phases, which modified the stabilities of coexisting metallic and insulating phases through the self-organization of competing phases. This in turn affects the control of the spatial extent of phase transitions and the electrical characteristics of the Mott transition. In this regard, the engineering of surface energetics through controlling of the surface structure and crystallographic growth directions in one-dimensional (1D) nanoscale building blocks with high surface area is extremely important in modifying and designing 1D Mott transition systems, especially in VO2. For example, one-dimensionally aligned metal–insulator domain walls were reversibly created and eliminated along a single VO2 nanobelt by varying the temperature, which allows for the accurate extraction of the net contribution to the Seebeck effect from these domain walls 44.
The huge and sharp drop in the NIR transmittance and resistance as well as many abnormal electrical and thermal phenomena in the IMT process have attracted significant attention due to the great potential in applications of smart coatings, ultrafast switches, and so on. Additionally, samples with different sizes are also discussed for their different properties and research purposes. However, there remain several puzzles regarding the intrinsic nature of this transition, such as the specific correlation, the formation of the band gap, etc., which will be discussed in the next chapter in detail.
Research on the phase-transition mechanism
Over the past 20 years, elucidating the physical properties of the phase-transition system has been one of the most challenging subjects in condensed matter physics and continues to pose controversial theoretical, as well as experimental, issues. In the transition of the VO2 system, the Mott correlation, Peierls distortion, and orbital split occur in the V–V chains simultaneously, which creates multiple problems with our understanding of the mechanism. In this chapter, we will highlight the focus of the mechanism research and the significance of the VO2 phase-transition characteristics for later modulation. Additionally, the controversial issue mainly lies with the theoretical explanation of the lattice–electron interactions and the electron–electron correlation in the phase transition.
Peierls phase transition
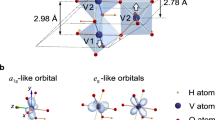
In 1930s, Rudolf Peierls, theoretically, assumed that the 1D conductor is composed of atoms of equal spacing (lattice constant a), each with a conduction electron50. Because of the interaction between electrons and the lattice, this 1D system is unstable, and lattice distortion occurs at pairs of atoms at low temperatures. When the modulation wave vector q = 2k (k: Fermi wave vector), the Fermi surface and the boundary of the Brillouin zone are completely “nested”. When the energy dissipated by the opening of the band gap is greater than the elasticity of the lattice distortion, the energy of the whole electronic lattice system is reduced, resulting in the transition of the system from a conductor to an insulator. Goodenough first used crystal field and molecular orbital theories to study the electronic structure of VO2, and he thought that the lattice distortion caused the MIT transformation, belonging to the Peierls transition51. He believes that in the rutile VO2 phase, the V3d orbital splits into a1g, egπ, and egσ due to the octahedral crystal field. When VO2 changes from the tetragonal phase to the monoclinic phase, V atoms are transformed from the original linear isometric form into a zigzag V–V dimer configuration. Additionally, the dimerization induces the a1g orbital division and the orbital energy increase. Finally, a band gap appears between the a1g orbital and egπ resulting in a metal-to-metal transition. After that, Wentzcovitch et al.26 calculated the electron and lattice structures before and after the VO2 phase transition using the local density approximation (LDA). The results supported Goodenough’s point. They found that the emergence of the band gap is mainly due to an enhancement of the V–V bond (mainly the V-orbital overlap of the V–V dimer), which is consistent with the monoclinic M1 phase in the experimental results. There are also many studies that support the VO2 MIT belonging to the Peierls phase transition. For example, Liebsch et al.52,53 studied the VO2 phase transition caused by local Coulomb interactions using a quasi-particle spectral method. It is found that the polarization of the t2g orbital is weak, but it has a strong dynamic correlation; while in the M1 phase, due to the V–V Peierls distortion, the 3d orbital polarization is strong, resulting in a strong static correlation. They argue that Peierls phase transition is the main cause of the VO2 MIT. In 2014, Budai et al.54 reported that anharmonic phonons drive the VO2 phase transition using X-ray and neutron scattering margins, revealing the importance of the lattice vibrations in the VO2 phase-transition process. By calculation, they found that the process of converting VO2 from the rutile metal state to the monoclinic state is the process of orbital selectivity (the occupied dxz and dyz are reduced, and the occupied dx2−y2 is increased), lowering the energy of the system and opening the band gap of the insulating phase (see Fig. 5). Additionally, the energy reduction caused by the Peierls distortion leads to the VO2 MIT.
a Energies, b forces, and c orbital occupancies of the intermediate structures between the rutile (ξ = 0) and M1 (ξ = 1) phases54. Copyright© 2014 Nature Publishing Group
In conclusion, the Peierls phase-transition mechanism qualitatively explained that the V–V dimerization induced the opening of the band gap. However, the VO2 MIT is significantly more complicated, and the Peierls mechanism does not completely explain all phase-transition problems. For example, the Peierls mechanism still cannot accurately explain the clear experimental band gap of 0.6 eV for the M1 phase, the appearance of a metastable phase (M2 phase), the magnetic features of the MIT, etc. Essentially, the Peierls mechanism is a result concluded from traditional band theory. However, traditional band theory fails to explain a band gap as large as 0.6 eV in the single-particle spectrum obtained from the monoclinic structures based on density functional theory (DFT) within the LDA or generalized gradient approximation (GGA)26,55. It seems that the Peierls mechanism has ignored some pivotal factors in the phase transition, or in other words, traditional band theory does not fit well with VO2 materials.
Mott phase transition
Based on the discussion of the above section, the lattice distortion in the V–V chains may actually induce the opening of the band gap. However, there are still a series of unresolved problems with the Peierls perspective. Particularly, quantificationally, the obtained M1-VO2 band diagrams based on traditional band theory have a narrower (or even absent) band gaps (Fig. 6a, b), which is contradictory to the experimental band gap of 0.6 eV.
Calculated using the a, b GGA and the c, d HSE functionals125. Copyright© 2011 the American Physical Society
In fact, this anomalous conductivity is very common in TMOs56. TMOs have always been a very special kind of material. Their uniqueness lies with the highest occupied orbital of metal atoms usually being derived from d electrons and f electrons. These electrons not only are far away from the nucleus but also sometimes exhibit spin polarization. In the conventional DFT (including LDA and GGA) calculations, the electron–electron repulsion of the Kohn–Sham equations is still based on a single-particle approximation57,58. The electronic exchange function sees spin-pair electrons as single particles, in which case, the number of K–S orbitals is half of the total number. However, when dealing with d/f electrons, we have to split the electron pair into two particles, spin up and spin down. When using the exchange-correlation function of the single-particle approximation for open-shell systems, the related functionalities cannot fully consider the correlation effects of d/f electrons. The related effects of d/f electrons are the mutual repulsion between spintrons and the repulsion between spintrons and inner electrons. These repulsive effects make the orbital/band division between the far orbital/band narrow. However, the related functional of DFT does not take these repulsions into consideration. As shown in Fig. 6a and b, the obtained M1-VO2 band diagram has no obvious band gap, which is contrary to the experimental band gap of 0.6 eV.
For the repulsion of d/f electrons, an additional Hubbard energy (U) could be introduced into the calculation of VO2 material energy states. The Hubbard energy can represent the secondary derivative of the energy to the electron density change on the d/f orbital. The energy band diagram obtained by the calculation with LDA+U is in good agreement with the experimentally obtained band gap, though a few questions still existed such as the wrong descriptions for the conduction and magnetism of R-VO259. In addition to the DFT method, with the rapid development of computer technology, the GW approximation (The approximation based on the single paticle Greenʼs function G and screened Coulmb interaction W) and hybrid functional theory have been used to explain the wide band gap of M1-VO2 well (see Fig. 6c, d)21,60,61,62. All of these computational theories explained the exchange interaction of electrons more accurately. In other words, the consensus at the moment is that some amount of U is necessary to describe the insulating nature of M1-VO2.
Another important problem that cannot be explained by the Peierls mechanism is the emergence of other intermediate phases. During the past few decades, in addition to the M1 and R phases, some other insulating phases have been gradually observed, such as the monoclinic M2 phase, the M3 phase, and the triclinic T phase. Among them, the M2 phase has been studied frequently, as it has similar dielectric properties but different magnetic properties compared with the M1 phase. In the M1 phase, both the metal–metal pairing and the zigzag-type lateral displacement are observed on each chain, whereas in the M2 phase, only half of the chains dimerize, and the zigzag-type deviations are reserved to the other half of the chains. The emergence of these new phases seems to present great difficulties in directly studying the phase transition; however, it would be important to understanding the mechanism of the MIT if these phases could be controlled freely. Furthermore, in M2 one-half of the V4+ ions form equally spaced V chains, and Nuclear Magnetic Resonance (NMR) and Electron Paramagnetic Resonance (EPR) experiments show that they behave magnetically as S = 1/2 Heisenberg chains (J = 300 K)63. It is clear that the V–V chains in M2 are magnetic insulators. Indeed, LDA calculations for the M2 phase lead to an antiferromagnetic ground state. Similar to the M1 phase, this failure could be cured by LDA+U calculations. The MIT in VO2 is usually learned as a function of T, but both of the strain and the interconversion between M1 and M2. The appearance of this triple point shows that in a completely stress-free VO2 material, as the temperature changes, a direct change from M1 to R can appear. With the occurrence of stress, we could control the phase-transition temperature and even complete the multi-phase conversion. The role of stress or doping in the VO2 system will be discussed later in the regulation section.
As discussed above, the main controversies, such as the broad band gap, the intermediate phases, etc., that remain with the Peierls perspective could be settled by introducing the additional Hubbard energy (U). It seems that both the lattice distortion and the electron correlation play important roles in the MIT process. However, the actual relationship between them remains undetermined. Furthermore, the simple application of the correlation energy would still induce a wrong description for the nonmagnetic M1/R phases, and a more accurate description of the electron correlation is required. In the next section, the coupling of lattice–electron and electron–electron correlations will be discussed, and an intermediate monoclinic-like structure will be introduced during the discussion.
The coupling of Peierls and Mott mechanisms
As mentioned, LDA and GGA calculations fail to explain the structural, electronic, and magnetic features of the MIT. The consensus at the moment is that some amount of U is necessary to describe the insulating nature of M1-VO2. However, whether R-VO2 is a strongly correlated system or whether U is necessary for the MIT has not been clarified yet. Therefore, the study of the causes of the band gap is very important for the later phase transition modulation. Actually, the phase-transition mechanism is very complex, and its electronic phase transition and structural phase transition occur nearly at the same time. Scientists have not yet reached a unified understanding of the VO2 phase-transition mechanism. However, many efforts have been tried to clarify the mechanism of the phase transition in VO2.
As described above, with the DFT+U method, it is correlations (the Mott–Hubbard mechanism) that are responsible for the insulating properties of the M1 and M2 phases of VO2. However, this method also results in antiferromagnetic insulating ground states for the rutile phase. Kim et al.64 obtained a more stable insulating phase in the magnetic and nonmagnetic R-VO2 band structure calculations with the DFT+U. The energy gaps and the magnetizations were obtained as 0.86 eV and ∼1.1 µB for the ferromagnetic case, with 1.25 eV and ∼1.1 µB for the antiferromagnetic case. If we set aside the strong correlation, the role that the Peierls distortion of V–V chains plays in the transition is a very important question. Since the Peierls transition is closely related to the phonon softening instability, the study of phonon dispersions in VO2 is expected to give a clue to understanding the mechanism of the MIT in VO2. Indeed, the phonon softening at q = R was once predicted to be responsible for the transformation from R-VO2 to M1-VO254. Comparing the DFT and DFT+U results, the normal modes of R in the DFT+U are consistent with the lattice distortions of VO2. It seems that the Coulomb correlation effect in R-VO2 plays an essential role in assisting the Peierls transition (Table 1).
Since evidence has been found that both electron–electron interactions and V–V dimerization distortions contribute to the transition from the insulating monoclinic phase to the metallic rutile phase, a focus could be what roles they actually play in the transition. The direct observation of the structural and electronic components of the transition in VO2 by simultaneously combining powerful spatially resolved and energy-resolved probes of the crystal and electronic structures has been used in the research of the transition mechanism. In 2010, Yao et al.65 used temperature-dependent in situ X-ray absorption fine structure (XAFS) combined with DFT calculations to study the mechanism of the transition. The results showed that the VO2 metallization occurs in the intermediate monoclinic-like structure with a large twist of V–V pairs when the δ angle is smaller than 1.4° (see Fig. 7). In addition, with the development and maturation of various in situ observation techniques, Laverock et al.37 reported a simultaneous measurement of the structural and electronic components of the MIT of VO2 using electron and photoelectron spectroscopies and microscopies. They showed that these components evolve over different temperature scales and are separated by an unusual monoclinic-like-metallic phase. The correlation between structural kinetics and electronic structure indicates that the structural rearrangement is a key factor to the narrowing of the insulating band gap.
a A plot of the twisting angle vs. temperature and b the temperature dependence of the resistance during the thermal cycle of heating and cooling. c The DOS of the intermediate VO2 structure at different temperatures calculated by using the density functional theory method65. Copyright© 2010 the American Physical Society
The discovery of such a monoclinic-metallic phase leads us to turn our attention to electron–lattice interactions. As such, it is not difficult to find that the orbital split also plays an important role in the phase transition. Therefore, the MIT is the result of the interactions and competition among electrons, orbitals, and lattices. In addition, in both phases, spin degeneracy is stabilized by a correlation-driven delocalization of the V 3d electrons. Based on this, the metallization of the monoclinic phase becomes a very important and challenging part of understanding the transition. The great challenge comes from the limitation of currently available characterizations, in that it is indeed hard to capture intermediate electronic states in spatial isolation because of their transient occurrence.
Efforts on distinguishing the effects of Peierls and Mott mechanisms
So far, a clearer picture has been presented to us, which shows a two-step transition from the Mott correlation to Peierls distortions. Furthermore, these two steps are not independent of each other but closely connected with the orbital split. Additionally, the interaction between these two steps could be the focus of future mechanism research. In 2006, an unexpected intermediate non-equilibrium state called the monoclinic and correlated metal (MCM) was put forward to support the hole-driven Mott-type transition. A time-resolved transmissive pump-probe experiment was undertaken to describe the causality between the MIT and the SPT by analyzing coherent phonons in high-quality VO2 films. The Ag peak at 5.8 THz disappearing near 58 °C is attributed to the MIT active mode. The SPT temperature was regarded as 77 °C where the coherent phonon peak at 4.5 THz appeared. Thus, the MCM phase could be in a temperature range from 62 to 77 °C. In 2014, Morrison et al.66 reported a photoinduced metal-like phase of monoclinic VO2. In the experiments, polycrystalline VO2 films grown by pulsed laser deposition, initially in the low-temperature M1 phase (at ~310 K), are subject to optical (800 nm) excitation with 35 fs laser pulses. The time dependence of the changes in structural and electronic properties after optical excitation of the material are determined using pump-probe UED and time-resolved IR transmittance measurements. They believe that in this metastable metal phase, photoexcitation only results in occupancy rearrangements of the dxy and dxz orbitals and are not enough to change the periodic distortion of the lattice. The lattice distortion requires a stronger excitation light, which also shows that the primary latent heat of the MIT mainly comes from the structural phase transition (Discussed in detail in Section Light irradiation).
With reference to band theory, if electron or lattice perturbations were introduced into this material system, the changes in electronic and lattice structures could bring us an abundance of information. For example, recently, Li et al.67 reported a surface coordination route to experimentally stabilize and directly image a metal-like monoclinic phase in the MIT. The AA molecules were used for chelation of the surface of VO2 nanobeams to induce a 1D charge carrier density reorganization, triggering a nonequilibrium metallic state in monoclinic VO2 (see Fig. 8). The authors implied that when the injected electrons were sufficient, the rutile metal state could be stabilized up to room temperature. While in the metal-like monoclinic region, owing to less injected charge, the electron density in this portion was insufficient to suppress the Peierls distortion of the monoclinic lattice, unraveling the orbital-selective Mott correlation for the gap opening of the VO2 MIT.
Left panel: the metal rutile phase, middle panel: the insulating monoclinic (M1) phase, and right panel: intermediates of the metal-like monoclinic (M1*) phase with the proposed band diagram67. Copyright© 2017 Nature Publishing Group
For a deeper and better understanding of this transition, researchers have not limited their studies to the simple VO2 or the influence of perturbation on the phase transition. A variety of modulation methods (electron injection, lattice control, etc.) have been widely studied and applied and are thought to provide a deeper understanding of existing theories. Similarly, the existing understanding of the phase transition characteristics also provides guidance and assistance to the modulation measures.
Modulation of the VO2 MIT
As we all know, VO2 differences in resistance and IR light transmittance before and after phase transition impart great application prospects in ultrafast optical and electrical switching devices. However, the transition is mainly dependent on the temperature, which is approximately 340 K, and it still limits practical applications because of the uncontrollability of the temperature. Therefore, the effective control of the VO2 MIT temperature has always been the most desirable goal for researchers. From the above discussion, we can see that the electron-orbital-lattice correlations could be responsible for the phase transition. Although we still cannot clarify the true connection among these factors, including the sequence of the phase transition and the origin of the insulating gap, it does not prevent modulations of the transition characteristic with these elements. Based on the modulation of the carrier or the lattice, multiple methods have been used in the field, such as elemental doping, stress regulation, and so on. Additionally, there are also a few studies regarding the modulation of orbital occupation, such as dielectric induction, photoexcited transition, etc. The following details several current effective VO2 MIT regulatory approaches.
Elemental doping
Doping is a classical method to control the carrier concentration of materials. Depending on the incorporation of the elements, electron injection or hole injection of the parent material can be caused. Studies have shown that doping is an effective means of regulating the VO2 MIT51. For example, W6+, Mo6+, and Nb5+ are used to reduce the VO2 MIT temperature68,69, and W6+ is the most effective one (Fig. 9)70. For a single-crystalline VO2 nanobelt sample, the transition point exhibits an approximately linear decrease with the amount of dopant, which is approximately 18.4 °C/at.%, while for polycrystalline films and powders, the values are approximately 24 °C/at.% and 25–26 °C/at.%29,71,72. It has also been found that the effect of W-doping may involve more than the injection of electrons by also inducing lattice strain, which may play an important role in the reduction of the VO2 phase-transition temperature73. Additionally, on the other hand, low-valence metal ions, such as Cr3+,Ga3+, and Al3+, are used to increase the temperature of the phase transition 74,75.
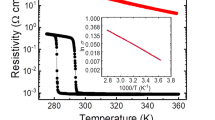
a (0<x<0.08) and b (0.09<x<0.33). The metallic resistivity at low temperatures appeared for 0.08<x<0.0970. Copyright© 2010 AIP Publishing
Jamie et al.76 used the absorption fine structure spectrum to study the structure of W-doped VO2, and they found that the introduction of W atoms not only broke the symmetry of the lattice but also increased the spacing between the cations. The results showed that the cell expansion precedes the occurrence of V–V bond breakage in the c-axis direction of the crystal. For example, in Fig. 10, 1.0% W-doped VO2 retains the insulating phase, while a 1.9% dopant concentration converts it into a metal phase with the V–V pairs exhibiting no significant change. This strongly shows that lattice expansion is the key to the occurrence of the phase transition, which is the point of the Peierls phase-transition view.
a The rutile phase and monoclinic phase of W-doped VO2. b Vanadium K-edge data of a 1% doped sample below its MIT and juxtaposed with a 1.9% doped sample undergoing its MIT76. Copyright© 2009 the American Physical Society
In recent years, hydrogen doping has been widely used to regulate the carrier concentration of the material. Hydrogen is a strong electron donor, while its atomic radius is very small. The injection of hydrogen atoms does not cause a large distortion of the lattice compared with metal-ion doping, avoiding the formation of too many defects. Hydrogen doping has been widely used for electronic structure regulation in TMOs and chalcogen compounds. For example, Natelson et al.77 achieved the stabilization of the metallic state of VO2 by the use of catalytic spillover in 2012. They first evaporated a layer of a Au film at one end of VO2 nanobelts and placed them in a tube furnace, heated to 180 °C for 12 h in a hydrogen atmosphere and then cooled to room temperature. Here, the Au film acts as a catalyst: the H2 molecules are decomposed into H atoms on the surface of the Au thin film under heating, and then, the H atoms are doped into the VO2 nanobelts. Through a variable-temperature conductivity test, the researchers found that the hydrogen-doped metal-state VO2 nanobelts can be stabilized to 4.2 K. They tried to hydrogenate the VO2 nanobelts at different temperatures and found that the doping of hydrogen could reduce the resistance of the monoclinic phase, which, however, had little effect on its transition point. When the hydrogenation reached a certain degree, the phase-transition point disappears, which is different from W-doping, to achieve a continuous phase transition.
In 2016, Hyojin et al.78 demonstrate a two-step insulator-to-metal-to-insulator modulation as the hydrogen concentration increases. They formed nano-sized Pt islands on epitaxial VO2 layers and annealed the samples under forming gas containing 5% hydrogen gas at 120 °C. The STEM and resistivity results showed that the samples underwent a transition from insulator (M-VO2)-to-metal (HxVO2)-to-insulator (HVO2) (as shown in Fig. 11a, b, c). Later the authors analyzed the electronic structure of the insulating HVO2 phase by X-ray photoemission spectroscopy, near-edge X-ray absorption fine structure (NEXAFS), and first-principles calculations. The results showed that the Peierls V–V dimerization was less pronounced in HVO2 than in M-VO2, but electrons supplied by hydrogens expanded the lattice through an electron–lattice coupling, which seemed to trigger a stronger electron correlation in narrow d bands and created the band gap in the insulating HVO2 phase. Recently, Chen et al.79 reported a facile approach to hydrogenate monoclinic VO2 in an acidic solution under ambient conditions by placing a small piece of low-work-function metal (Al, Cu, Ag, Zn, or Fe) on the VO2 surface. Additionally, the later successful doping of Li+ into VO2 suggests a general atomic doping approach of using a proton or cation solvent source together with electrons from metals.
a HAADF-STEM and b ABF-STEM images of the (100) fully hydrogenated HVO2 epitaxial film grown on TiO2(100) substrates with a [001]R zone axis. c The temperature-dependent sheet resistance in HxVO2 thin films from plot I to plot IV with increasing hydrogen content (x)78. Copyright© 2016 Nature Publishing Group. d A schematic illustration of the contiguous electron–proton co-doping mechanism with the metal-acid treatment of a semiconductor: First, the electrons flow to the semiconductor when the metal contacts the VO2 film. Once the metal/VO2 is immersed in the acid solution, the chemical reactions proceed sequentially as M–x[e−] → Mx+ and VO2 + x[e−] + x[H+] → HxVO279. Copyright© 2018 Nature Publishing Group
In general, using the element doping (metal ion, H, etc.), we could regulate the carrier concentration of VO2 materials effectively and obtain continuous transition points with a gradient doping concentration. However, this kind of electronic modulation could be nonreversible and uncontrollable. As mentioned above, the doping of elements even as small as H atoms would bring unavoidable and unpredictable lattice distortions70,78. When the lattice distortion reaches a certain value, the effect for the MIT modulation would be negligible or even the opposite. Furthermore, the doping elements are generally restricted by the inhomogeneity of the elemental distribution, which would affect the whole of the MIT properties greatly. Moreover, the hydrogenation techniques available are not sustainable as they are conventionally performed with noble-metal (Au, Pt, and Pd) catalysts, a high-temperature/pressure annealing treatment or high-energy proton implantation under a vacuum condition80,81. A more controllable method to dominate the phase transition seems ready to be discovered.
External electric field
The most intriguing nature of VO2 materials could be the sharp resistance (IR transmittance) change of approximately three to four orders of magnitude near 340 K. From a practical point of view, we would be glad to create a controllable and reversible trigger temperature, or even a convenient trigger, rather than heating directly. Answering this question would provide a better determination of the scope for utilizing VO2 in ultrafast electronic devices, as well as open an alternative direction in modulating other correlated materials. As a controllable and convenient means, electrical control has a great prospect in this regard. In fact, several efforts have been put into the transition modulation. However, the mechanism of the electrical triggers could be not the same exactly and might come from electron injection, Joule heating effects, dielectric attraction, or ion doping. Here, we divide this section into two subsections: two-terminal and three-terminal electrical triggers. The detailed introductions follow.
Electrical current heating
In 2000, Stefanovich et al.82 reported that electric field or electron injection into VO2 can trigger the MIT. Additionally, an abundance of follow-up two-terminal switches utilizing the electrically triggered MIT have been reported83,84,85. For example, Leroy et al.86 reported a fast MIT phenomenon of the VO2 thin film in the picosecond range induced by an electric field pulse voltage (see Fig. 12). In 2004, Kim et al.87 reported that the critical voltage of the MIT phase was decreased as the temperature increased, and the Raman results showed that holes were excited by the increase in temperature. Moreover, the authors also tried to study the VO2 MIT mechanism. They compared the hole-driven MIT model (an extended BR picture, the idea of this research) with the Aronov Kudinov model (the AK model can be regarded as the Peierls picture88). The results of the Raman experiment showed the structural phase transition was secondary.
The inset displays the temperature dependence of the VO2 layer resistivity (four-probe measurements)86. Copyright© 2012 AIP Publishing
Investigators have argued that the Joule heating effect from leakage current is likely to trigger the MIT. In 2013, Wang et al.6 prepared a two-terminal device using a single VO2 NW. They found that when a voltage of 0.34 V was applied without heating, the MIT of VO2 nanobelts occurred (Fig. 13a), and this transition with the voltage reduction was reversible and could be used for fast memory device circles (see Fig. 13b, c). It was believed that the Joule heat generated by the addition of the voltage was the cause of the MIT of the VO2 nanobelts, which reduced the metal-state resistance; when the external voltage was not applied, it became the insulating state, and the resistance increased. Interestingly, Chen et al.89 reported free-standing SWNTs/VO2/mica hierarchical films for high-performance thermochromic devices. The single-wall nanotube (SWNT) layer is used as a heating controller, and by adjusting the bias current, it is possible to change the starting local temperature and shift the initial situation close to the “phase transition boundary”, resulting in a decreased energy barrier to trigger the MIT behavior, as shown in Fig. 13d. Though the effects of the current heating modulation have been applied, there may be many restrictions for later applications and research. It is still a thermal phase transition essentially influenced by many factors, which could be uncontrollable. The environmental heat exchange and unstable current could bring a nonlinear and uncertain heating process. Furthermore, the inverse process from the rutile phase to monoclinic phase could be uncontrollable and hysteretic due to a difficult cooling process.
a Schematics showing the gradual change of phases inside a nanowire. The black and white parts denote the metallic and insulating phases. b The resistance of annealed VO2 nanowires at room temperature with a 0.3 V bias. The 30 V, 20 V, and 10 V pulses are applied for 0.25 s. The inset graph shows the change for 5 min with a 20 V bias. c The resistance–voltage (R–V) hysteresis curve6. Copyright© 2013 John Wiley and Sons. d After applying a bias current on a hybridized device, the device temperature moves close to the phase transition boundary (area denoted by the red open rectangle)89. Copyright© 2017 Elsevier
Electric field gating
As described above, it has been proven that a current flow could heat the VO2 materials over the transition point in a two-terminal device, which could be disturbed with an inhomogeneous current flow. In a three-terminal gated device similar to the conventional field-effect transistor (FET), an electric field introduced by an applied external gate voltage can also modulate the transition, and the response could be reversible and nonvolatile at room temperature, compared to the two-terminal device. In other words, three-terminal electronic switches utilizing the E-MIT may potentially demonstrate functional Mott-FETs for applications in the RAM-like semiconductor industry. Additionally, this modulation could be mainly due to many causes, including electrostatic carrier doping, electric field-induced strain or field-induced chemical carrier doping.
In the early proposed three-terminal VO2 switch device, as shown in Fig. 14a, the VO2 was deposited on the dielectric substrate as a carrier channel, and a gating dielectric layer was deposited on the VO2 film as a gating switch functionally. For example, Sengupta et al.90 designed a HfO2/VO2/SiO2/Si three-terminal device with sputtered Cr/Au as drain–source (D–S) electrodes. They found that the conductance could be influenced by the gate voltage, as shown in Fig. 14c, d, and the response was reversible and hysteretic, with the area of the hysteresis loop potentially affected by the rate of the gate sweep. There are also many other dielectric materials used for the gating layer. Kim et al.87 used a SiO2 layer as a dielectric gating layer, and specially, the SiO2 was underneath the VO2 thin film, as shown in Fig. 14b. In addition, they found that the source–drain current density was a function of the electric field under different applied negative gate voltages, as shown in Fig. 14c. Researchers have argued that the resistance switching was ascribed to the Mott transition due to the carrier injection (electrons or holes) from the gate into the VO2 channel.
a An early proposed three-terminal gated VO2 switch device. b Current density versus electric field applied on the VO2 channel with the gate open at room temperature. The inset shows the three-terminal VO2 device structure. c Current density versus electric field applied on the VO2 channel with applied negative gate voltages at room temperature87. d Conductance as a function of gate voltage (Device 3) for two different cycle times: 10 mins (red) and 27 mins (blue)90. Copyright© 2011 AIP Publishing
In fact, limited by the breakdown voltage and leakage current, this electrostatic gating method could have high requirements for the permittivity of the dielectric layer, film quality, and gating field. High-quality films could endure application of a larger gate voltage and create a larger field in the channel91. Furthermore, the thickness of the dielectric layers and VO2 channel could also influence the performance of the device, as thinner conformal VO2 layers could increase the field penetration into most of the channel region. Moreover, in an ideal three-terminal device, the source–drain (S–D) current would be kept small and well below the value that can cause any heating of the VO2 channel, and even the leakage current should be significantly smaller than the S–D current for a high electrostatic field without destroying the samples. The conventional gate dielectrics could cause an accumulation of electronic charges on the order of 1 × 1013 cm−2, which extend be beyond the electrostatic length. Additionally, there are also some reports attempting to search for higher-permittivity gate dielectrics to realize higher electrostatic fields. For example, Yajima et al.92 reported a new structure of the inverse-Schottky-gate geometry using VO2/TiO2. A single-crystalline niobium-doped TiO2 (Nb:TiO2), an N-type semiconductor, is used as the substrate and also a back-gate electrode (high permittivity above 100), and the VO2 channel is regarded as a metal electrode. This high permittivity to high electric fields enables electrons of more than 1 × 1014 cm−2 to accumulate at the VO2/Nb:TiO2 interface, and TMIT has a negative linear correlation with the accumulated electron density (N2D) (the N2D to decrease TMIT by 1 K is ~9.0 × 1013 cm−2). However, this kind of transition modulation is still not enough for the electrical trigger.
Because of many restrictions, the dielectric gate could not provide sufficient interfacial electric field for triggering the MIT, being limited by the gate leakage current. The electric double-layer transistor (EDLT) with an ionic-liquid (IL) gate dielectric is an alternate approach to conventional solid-gate insulators (N2D≈1014 cm−2) and has been utilized to investigate the field effect in various semiconducting and correlated oxides. Ramanathan and colleagues93,94 first reported the study of an IL-gated field-effect device fabricated with VO2 thin films on sapphire substrates. The VO2 channel resistance decreases by approximately 50% at a +2 V gate bias. Later, they95 compared this ionic liquid gating process on a sub-50 nm VO2 membrane with the hydrogen annealing process, and they found these two processes could be different. In July 2012, Tokura’s team19 found that electrostatic charging at a surface could drive all the previously localized charge carriers in the bulk material into motion, as shown in Fig. 15a, leading to the emergence of a three-dimensional (3D) metallic ground state. They suggested that the presence of a strong electron correlation and electron–lattice coupling broke down the shielding effect in the traditional FET. Later, Ji et al.96 reported attempts to modulate this transition in single-crystalline VO2 NWs via electrochemical gating using ionic liquids. They found that stray water contamination in the ionic liquid was critical for the modulation, suggesting a result of electrochemical doping via hydrogen. In 2013, Parkin and colleagues20 found that the electrolyte gating of VO2 leads not to electrostatically induced carriers but instead to the electric field-induced creation of oxygen vacancies. Compared with the voltage gradient experiment, they were deposited on the same substrate with different oxygen pressures to grow VO2 films. The results of the temperature-dependent resistance and XPS characterization are consistent with the oxygen pressure and the E-gating. This allows them to conclude that the suppression of the transition is the result of the oxygen vacancy formation during electric field gating. There were also many other reports trying to explain this E-MIT from the electrochemical doping perspective.
a Schematic of an electrical double-layer transistor (EDLT) based on VO2, potentially enabling electrical switching of the MIT between the metallic tetragonal phase and the insulating monoclinic phase. b Electronic phase diagrams of electrostatically and chemically doped VO2 films19. Copyright© 2012 Nature Publishing Group
Recently, Yu et al.97 reported a reversible and non-volatile electric-field control of dual-ion (oxygen and hydrogen) phase transformations. They showed that controlling the insertion and extraction of oxygen and hydrogen ions independently of each other could direct a reversible phase transition. Furthermore, they proved that the oxygen or hydrogen ions came from the impurity water. Interestingly, based on the consideration of electrochemical doping, Sasaki et al.98,99 demonstrated a new method to realize the electric-field-induced hydrogenation of VO2 NWs without ionic liquids using the nanogaps separated by humid air. As shown in Fig. 16a, compared to the method in dry air, the change in resistance is nonvolatile and reversible in the humid air. The water in the humid air plays the critical role of a gating switch (also called a doping source) instead of ionic liquids or solid dielectrics. Moreover, many other electrochemical doping elements (Li+, K+, etc.) have been proven to be valid in a similar way. Interestingly, You et al.100 designed a multilayer structure of electrolyte/graphene/VO2 that showed selectivity for different ions. In such an EDLT, the graphene layer serves as an insert barrier that could protect the oxide surface from chemical reactions. As shown in Fig. 16b, c, compared to the bare VO2 film, the graphene-coated VO2 remains unchanged for over a thousand minutes under a critical applied bias.
a The typical architecture and an atomic force microscope (AFM) image of the electric field-gating device using the nanogaps separated by humid air98. b A monolayer of graphene is interfaced between the electrolyte and VO2 to protect the oxide surface. Copyright© 2015 Nature Publishing Group. c Time-dependent modulation of the channel resistance of bare VO2 and graphene-coated VO2 under a constant gate voltage of 2.5 V100. Copyright© 2015 American Chemical Society. d A schematic drawing of the cross-section of the hybrid gate setup104. Copyright© 2016 the American Physical Society
The electrochemical gating of VO2 is, in general, composed of two regions. When the electrochemical gate voltage is low, the gating is purely electrostatic. As the gate voltage further increases, chemical reactions occur, and ions may intercalate into the VO2, which are balanced by the changed electron concentration in VO2. Many follow-up detailed studies have been discussed by latter reports about the electrochemical reaction. Jeong et al.101 reported a giant structural change induced by ionic liquid gating in which the lattice expands by up to ∼3% near room temperature, in contrast to the 10 times smaller (∼0.3%) contraction when the system is thermally metallized. Furthermore, the substrate could affect the reversibility of the gating effect. Nakano et al.102 reported that VO2 films grown on the hexagonal Al2O3 substrates show irreversible gating effects from the permanent reduction of the valence state of vanadium during a gate-induced metallization process. Chen et al.103 reported that the diffusion of the ions could be influenced by the gate voltage and the gating time in films compared to that in nanobeams within the nanometer scale. As gating time increases, the electrochemical doping diffusion could reach deeper positions reflected in the structural transition (Raman) intensity and light transmission. It was noted that the sheet resistance could only represent the conductivity of the shallow part. All in all, the ionic gating method could be substantially more effective than the dielectric gate method. However, the process could be limited by the ion transfer including ion diffusion and charge compensation, which could induce an inefficient and hysteretic gate modulation. Peng et al.104 demonstrated a new hybrid gating technique by adding the extra capacitance of a dielectric substrate, as shown in Fig. 16d. Charge accumulates at both sides of the double layer, forming an efficient capacitor. Compared with the traditional liquid gating method, the hybrid gating technique allows for a significantly faster scan speed and results in a substantially smaller hysteresis.
In a word, the methods to reduce the transition point or trigger the phase transition electrically create the potential for novel switching devices. However, the current-induced heating effect or dielectric effect were likely insufficient to trigger the MIT due to uncontrollable heat flow or insufficient carrier induction. Additionally, the ionic electrolyte gating could be subject to the liquid mobility and slow ion-diffusion. The future research directions in this topic could be the construction of fast-ion-conductive layers to quickly achieve critical carrier densities.
Light irradiation
Optical excitation has been proven to be another effective method to control the phase transition in VO2105,106. As shown by Roach and Balberg back in 1971107, the ultrafast laser as a powerful tool could induce a fast transition, which is regarded as a photo-electron–phonon energy transfer process. As mentioned above in the mechanism discussion, the main debate of the transition mechanism comes from the lattice and electronic contributions. Similar to the thermal transition, the study of lattice and electron dynamics could be the focus of the modulation mechanism, which could also provide evidence for the origin of the band gap.
In 2001, Cavalleri et al.108 used femtosecond X-ray and visible-light pulses to study the structure and electron transition kinetics of the optically driven VO2 MIT. They found that laser pulses of sufficiently high fluence could trigger a sub-picosecond structural transition from the low-T monoclinic phase to the high-T rutile phase (see Fig. 17). Additionally, they argued that the structural phase transition at the beginning may not be driven thermally for the insufficient heat flow triggering the transition.
a The angle-dependent x-ray diffraction signal measured for negative and positive time delays. The diffraction profiles originate from the convolution between the rocking curve of the dynamically strained/transforming crystal and the spectrum of the x-ray plasma source. The dashed and continuous curves correspond to delays of 2300 fs and 11 ps. b The ratio between the x-ray reflectivity of the excited and unpumped crystal108. Copyright© 2001 the American Physical Society
After that, a large number of papers reported this ultrafast photoinduced response, and a non-thermal transiently metallic monoclinic state (mM phase) has been found in the time domain, which means that the characteristic time of gap-closing (τgap) preceded the characteristic of changes in the lattice (τlattice)66,109,110. Research has attributed this sequence to the emergence of photoinduced holes at the top of the valence band. As shown in Fig. 18, in the initial step, the optical excitation promotes electrons from the VB to the CB, and then, the band gap collapse occurs due to the change in the screening of the Coulomb interaction through the free carriers.
(1) Photoexcitation promotes electrons to the Conduction Band (CB) and leaves holes in the Valence Band (VB). (2) Intraband transitions increase the screening of the CIA and thereby close the band gap. (3) Thermalization of carriers within the energetic region of the former gap occurs slower than this band gap collapse126. Copyright© 2014 the American Physical Society
The instantaneous band gap collapse, which goes along with the generation of free carriers, is a consequence of the enhanced screening of the transient phase; however, the following crystallographic changes can still be discussed. This question could be answered by the change in potential with symmetry. The ultrafast dynamics in the optical response of the transient phase after strong photoexcitation are fundamentally different from the ones in the equilibrium monoclinic and rutile phases, which means that the lattice potential change occurs on a timescale (τLPC) shorter than τCPT.
Figure 19 gives an overview of the series of processes occurring during the photoinduced phase transition in VO2. First, photoexcitation above a certain critical fluence leads to a collection of electron transitions and a collapse of the band gap, and at the same time, the depopulation of the V–V bonding orbitals leads to a lattice potential change, as the new charge distribution changes the forces that act on the ions. The monoclinic potential symmetry is lost instantaneously with photoexcitation, representing the trigger for the CPT, which evolves over multiple subsequent timescales.
a Bright (left) and dark (right) field optical images of VO2 nanobeams. b A schematic diagram showing the periodic domain pattern of a VO2 nanobeam strained on a SiO2 substrate. c Spatial periods (λm) of the domain patterns as a function of the nanobeam thickness (t) for VO2 nanobeams embedded in SiO2 and Al2O3116. Copyright © 2006 American Chemical Society
In summary, based on the results discussed, the photoinduced phase transition mainly comes from the electron excitation. Additionally, the dynamics of the collapse of the insulating band gap and the origin of the V ionic motion could provide us with great opportunities to understand the nature of the phase transition. On the other hand, this ultrafast approach to disentangle electronic and structural phenomena in the time domain also offer a new way to observe the change in VO2 or in other material systems.
Strain engineering
Many experimental and theoretical studies have shown that strain is a good way to regulate the physical and chemical properties of materials7,111,112. Especially in strongly correlated electron systems, a continuously adjustable lattice strain is a sensitive method used to study phase heterogeneity. Because of the strong correlation of lattice strain, charge, spin and orbital113,114, induced strain can significantly affect the electrical, optical and magnetic properties of associated electronic materials115. The current source of strain in micro/nanoscale materials mainly comes from the lattice mismatch and elastic mismatch between the material and the substrate. According to the relative size of the mismatch, strain can be divided into tensile stress and compressive stress. For the VO2 thin film and single-crystalline nanostructures, the induced strain can effectively adjust the MIT.
Compared with the bulk and thin film samples, the single-dimensional and single-crystalline properties of VO2 nanobelts make them able to withstand large axial stresses without causing breakage and damage. As we know, different electronic states present a difference in optical color, and the coexistence of different phases in the state under strain can be observed directly under the microscope. There are three main ways to apply strain to the single-crystalline VO2 nanobelts. The first is to fix the VO2 nanobelts directly on the substrate and provide heat to the vicinity of the transition point. Because of the different coefficients of thermal expansion of the nanobelts and the substrate, the VO2 nanobelt and the substrate produces a relative strain, and then there is a coexistence of metal and insulator phases, showing recurring alternating metal and insulation phase domains. As shown in Fig. 20, Wu et al., in 2006, studied the effect of the substrate strain on the phase transition of VO2 nanobelts116. They found that the simple adhesion between the substrate and the nanobelt could change the relative thermodynamic stability of the metal phase (M) and the insulating phase (I), resulting in the simultaneous formation of periodic alternating M–I domain patterns. Like the effect of strain on ferroelectrics, epitaxial semiconductors, and magnetoresistance complex oxides, they believed that the observed patterns of the domains of M–I were the result of the competition between the domain wall energy and the elastic energy between the nanobelts and the tomb (elastic mismatch). Additionally, the thickness of the nanobelt and the elasticity were also important for this periodic arrangement of the phase domain.
For VO2 film samples, the presence of lattice mismatch between the sample and the substrate introduces the strain effect, causing a change of the transition point of VO2. The substrates used for the epitaxial growth of the film are mainly titanium dioxide, sapphire, single-crystalline silicon, and germanium. The thickness of the VO2 film117,118, the choice of substrate119, the choice of the base crystal surface120, the buffer layer, and other factors could influence the growth of the films. In 2013, Parkin and colleagues121 modulated the transition temperature by varying the thickness of the buffer layer between VO2 and the substrate (resulting in different epitaxial strains). Additionally, the results of polarization-dependent X-ray absorption spectroscopy measurements showed that the strain modulation was based on the orbital reconstruction (see Fig. 21).
a, b the metallic state and the insulating state for samples with various TMIT. c, d A schematic of the changes in the valence electron states of the metallic state and the insulating state as TMIT is changed121. Copyright© 2013 Nature Publishing Group
In 2014, Fan et al.117 modulated the transition point via controlling the thickness of VO2. Additionally, they determined that the electronic orbital occupancy was strongly affected by the interfacial strain. Recently, Lee et al.119 reported a new approach to control the MIT dynamics in epitaxial VO2 films by employing an intermediate template layer with a large lattice mismatch to relieve the interfacial lattice constraints, contrary to conventional thin-film epitaxy that favors a lattice match between the substrate and the growing film. They also proposed in situ real-time nanoscale imaging to reveal robust, undisturbed MIT dynamics even at preexisting structural domain boundaries, while a significantly sharpened MIT existed in the templated VO2 films, as shown in Fig. 22.
a, b Schematic diagrams showing the expected profile of lattice strain in epitaxial VO2 films on TiO2(001) a without and b with a SnO2 template. c, d In situ TEM images during the monoclinic-to-rutile SPT on heating in 300-nm-thick VO2 films (c) without and (d) with a SnO2 template. The rutile phase is represented by the red color. The temperature is ramped up at 5 K min–1 during these measurements. Insets indicate the measured nanobeam electron diffraction patterns of monoclinic (upper) and rutile (lower) phases for VO2/TiO2 and VO2/SnO2/TiO2 films119. Copyright © 2017 American Chemical Society
In conclusion, stress could be an effective modulation for MIT control regardless of 1D (quasi-1D) or 2D materials. However, the current main challenge is that this modulation cannot be continuous and reversible limited by the rigid substrate. As practical optical/electrical switching materials, to find a type of flexible substrate for VO2 growth is highly desirable. Recently, related studies have gradually been reported. As mentioned, Chen et al.89 reported a free-standing SWNTs/VO2/mica hierarchical structure for high-performance thermochromic devices, in which the mica layer shows excellent flexibility, transparency, and stability. It is noted that these reports only focus on the flexibility of substrates but ignore the interaction of the VO2 and the flexible layer. Additionally, future issues could be concentrated on the effect of continuous changing stress on the transition.
Conclusion
In summary, based on the near-room temperature MIT behaviors, VO2 materials exhibit the greatest potential for application in thermochromic devices and energy-efficient systems. In this review, we have outlined both the conventional strategies and recent progress made to reveal the intrinsic nature of the peculiar insulator and gap opening. For materials with strong correlation effects, single-electron approximated simple DFT calculations could not predict the electrical properties of the M1 phase correctly. Similarly, including the exact electron–electron interaction to some extent, calculations could also not satisfy the correct conduction, structure, and magnetism simultaneously. In other words, it is widely agreed that strong electron correlation or lattice distortion is not a sufficient condition to open an insulating gap. Moreover, the discovery of the monoclinic metallic (mM) phase showed us the dynamics of the interactions among the electrons, lattice and orbits. Based on the understanding of the transition mechanism, we have also summarized several modulating methods to control the physicochemical properties. By controlling the electron concentration, substrate strain, etc., bridges can be built between the atomic lattice, electronic structures, and orbital shift, offering alternative promising solutions to regulate the transition characteristics. Furthermore, based on the traditional transition modulations, many new continuous reversible regulating methods were put forward, such as ionic gating, hydrogen doping, flexible substrate growth, etc; however, these methods could still be limited to many factors, such as the mass transfer, epitaxial growth, etc. Regardless, the research about the internal nature of the transition provides us with a great platform to regulate the correlation effects in VO2 and build a road to understand other TMOs.
Future directions
Since Morin first reported the VO2 MIT phenomenon, people have learned the basic contours of the phase-transition mechanism with the deepening of this research. Furthermore, researchers have developed various means to modulate the transition point effectively, which have been used in a variety of physical devices. This review has summarized and discussed recent advances on the development of the transition mechanism and means to modulate the property of the MIT in VO2. Although research is still in progress to address problems that may hinder commercialization, substantial progress is still needed before the technology would become fully integrated into our lives. Below, the main findings and the needs for future research under each topic are summarized:
-
1.
Understanding of the interaction between the electron occupation and the V–V dimerization: though we have known the sequences of the MIT and the CPT, there is still debate on the origin of the lattice collapse, which could be a result of competing charge distributions in the phase transition or orbital rearrangements. This debate could be explained by follow-up studies of the nonequilibrium metallic state in monoclinic VO2, and breakthrough progress in this regard may provide a new perspective to regulate the electronic properties of low-dimensional correlated materials.
-
2.
Continuous and reversible modulation of the phase transition or even a controllable transition trigger: traditional modulation methods such as elemental doping are limited by the lattice distortion and inhomogeneity and could be non-continuous and irreversible. Additionally, with the maturing transition mechanism, many new modulation methods, such as carrier concentration regulation-based hydrogen doping and lattice symmetry competition based nanobeams strain modulation and FET-like ionic gating, were put forward, which however still contain many problems, such as slow ion diffusion, field hysteresis, etc. More mature solutions such as all-solid-state conducting layers and flexible epitaxial films (Chapter 3 for details) are expected to solve these problem, which would maximize the value of the phase transition.
-
3.
Based on the modulations, developing new functional devices: over the past 2 years, using VO2 materials, a variety of new application concepts have been proposed, such as an ultrafast response flexible breath sensor122, artificial skin123, etc. The emergence of new regulatory methods makes VO2 materials not limited to single-point passive regulation. This will greatly broaden the application scope for such materials.
References
Goodenough, J. B. Metallic oxides. Prog. Solid State Chem. 5, 145–399 (1971).
Imada, M., Fujimori, A. & Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 70, 1039 (1998).
Schwingenschlögl, U. & Eyert, V. The vanadium Magnéli phases VnO2n‐1. Ann. Phys. 13, 475–510 (2004).
Kasırga, T. S. et al. Photoresponse of a strongly correlated material determined by scanning photocurrent microscopy. Nat. Nanotechnol. 7, 723–727 (2012).
Liu, K. et al. Giant-amplitude, high-work density microactuators with phase transition activated nanolayer bimorphs. Nano Lett. 12, 6302–6308 (2012).
Bae, S. H. et al. The memristive properties of a single VO2 nanowire with switching controlled by self‐heating. Adv. Mater. 25, 5098–5103 (2013).
Hu, B. et al. External‐strain induced insulating phase transition in VO2 nanobeam and its application as flexible strain sensor. Adv. Mater. 22, 5134–5139 (2010).
Savo, S. et al. Reconfigurable anisotropy and functional transformations with VO2-based metamaterial electric circuits. Phys. Rev. B 91, 134105 (2015).
Kats, M. A. et al. Vanadium dioxide as a natural disordered metamaterial: perfect thermal emission and large broadband negative differential thermal emittance. Phys. Rev. X 3, 041004 (2013).
Morin, F. Oxides which show a metal-to-insulator transition at the Neel temperature. Phys. Rev. Lett. 3, 34 (1959).
Lysenko, S. et al. Light-induced ultrafast phase transitions in VO2 thin film. Appl. Surf. Sci. 252, 5512–5515 (2006).
Soltani, M., Chaker, M., Haddad, E. & Kruzelesky, R. 1 × 2 optical switch devices based on semiconductor-to-metallic phase transition characteristics of VO2 smart coatings. Meas. Sci. Technol. 17, 1052 (2006).
Lee, J. et al. Microspectroscopic detection of local conducting areas generated by electric-pulse-induced phase transition in VO2 films. Appl. Phys. Lett. 91, 133509 (2007).
Strelcov, E., Lilach, Y. & Kolmakov, A. Gas sensor based on metal− insulator transition in VO2 nanowire thermistor. Nano Lett. 9, 2322–2326 (2009).
Becker, M. F. et al. Femtosecond laser excitation of the semiconductor‐metal phase transition in VO2. Appl. Phys. Lett. 65, 1507–1509 (1994).
Yang, Z., Ko, C. & Ramanathan, S. Oxide electronics utilizing ultrafast metal-insulator transitions. Annu. Rev. Mater. Res. 41, 337–367 (2011).
Zhou, Y. & Ramanathan, S. Mott memory and neuromorphic devices. Proc. IEEE 103, 1289–1310 (2015).
Qazilbash, M. M. et al. Mott transition in VO2 revealed by infrared spectroscopy and nano-imaging. Science 318, 1750–1753 (2007).
Nakano, M. et al. Collective bulk carrier delocalization driven by electrostatic surface charge accumulation. Nature 487, 459–462 (2012).
Jeong, J. et al. Suppression of metal-insulator transition in VO2 by electric field–induced oxygen vacancy formation. Science 339, 1402–1405 (2013).
Biermann, S., Poteryaev, A., Lichtenstein, A. & Georges, A. Dynamical singlets and correlation-assisted peierls transition in VO2. Phys. Rev. Lett. 94, 026404 (2005).
Kang, L., Gao, Y. & Luo, H. A novel solution process for the synthesis of VO2 thin films with excellent thermochromic properties. ACS Appl. Mater. Interfaces 1, 2211–2218 (2009).
Sun, Y. et al. New aspects of size-dependent metal-insulator transition in synthetic single-domain monoclinic vanadium dioxide nanocrystals. Nanoscale 3, 4394–4401 (2011).
Tselev, A. et al. Symmetry relationship and strain-induced transitions between insulating M1 and M2 and metallic R phases of vanadium dioxide. Nano Lett. 10, 4409–4416 (2010).
Pouget, J. P. et al. Dimerization of a linear Heisenberg chain in the insulating phases of V1-xCrxO2. Phys. Rev. B 10, 1801–1815 (1974).
Wentzcovitch, R. M., Schulz, W. W. & Allen, P. B. VO2: Peierls or Mott-Hubbard? A view from band theory. Phys. Rev. Lett. 72, 3389 (1994).
Cavalleri, A., Dekorsy, T. & Chong, H. H. W. Evidence for a structurally-driven insulator-to-metal transition in VO2: a view from the ultrafast timescale. Phys. Rev. B 70, 2806–2810 (2004).
Haverkort, M. W. et al. Orbital-assisted metal-insulator transition in VO2. Phys. Rev. Lett. 95, 196404 (2005).
Jin, P., Nakao, S. & Tanemura, S. Tungsten doping into vanadium dioxide thermochromic films by high-energy ion implantation and thermal annealing. Thin Solid Films 324, 151–158 (1998).
Tan, X. et al. Unraveling metal-insulator transition mechanism of VO2 triggered by tungsten doping. Sci. Rep. 2, 466 (2012).
Li, X. et al. Direct evidence of tungsten clustering in W0.02V0.98O2 thin films and its effect on the metal-to-insulator transition. Acta Mater. 80, 16–24 (2014).
He, X. et al. Negative capacitance switching via VO2 band gap engineering driven by electric field. Appl. Phys. Lett. 106, 093106 (2015).
Kim, H.-T. et al. Raman study of electric-field-induced first-order metal-insulator transition in VO2-based devices. Appl. Phys. Lett. 86, 242101 (2005).
Yang, Z. et al. Dielectric and carrier transport properties of vanadium dioxide thin films across the phase transition utilizing gated capacitor devices. Phys. Rev. B 82, 205101 (2010).
Mott, N. F. The basis of the electron theory of metals, with special reference to the transition metals. Proc. Phys. Soc. 62, 416 (1949).
Atkin, J. M. et al. Strain and temperature dependence of the insulating phases of VO2 near the metal-insulator transition. Phys. Rev. B 85, 120–120 (2012).
Wegkamp, D. et al. Direct observation of decoupled structural and electronic transitions and an ambient pressure monocliniclike metallic phase of VO2. Phys. Rev. Lett. 113, 216402–216402 (2014).
Barker, A. Jr, Verleur, H. & Guggenheim, H. Infrared optical properties of vanadium dioxide above and below the transition temperature. Phys. Rev. Lett. 17, 1286 (1966).
Verleur, H. W., Barker, A. Jr & Berglund, C. Optical Properties of VO2 between 0.25 and 5 eV. Phys. Rev. 172, 788 (1968).
Balu, R. & Ashrit, P. Near-zero IR transmission in the metal-insulator transition of VO2 thin films. Appl. Phys. Lett. 92, 021904 (2008).
Chang, T. et al. Optical design and stability study for ultrahigh-performance and long-lived vanadium dioxide-based thermochromic coatings. Nano Energy 44, 256–264 (2018).
Lee, M. J. et al. Two series oxide resistors applicable to high speed and high density nonvolatile memory. Adv. Mater. 19, 3919–3923 (2007).
Ko, C. & Ramanathan, S. Observation of electric field-assisted phase transition in thin film vanadium oxide in a metal-oxide-semiconductor device geometry. Appl. Phys. Lett. 93, 252101 (2008).
Cao, J., Fan, W., Zheng, H. & Wu, J. Thermoelectric effect across the metal− insulator domain walls in VO2 microbeams. Nano Lett. 9, 4001–4006 (2009).
Oh, D.-W., Ko, C., Ramanathan, S. & Cahill, D. G. Thermal conductivity and dynamic heat capacity across the metal-insulator transition in thin film VO2. Appl. Phys. Lett. 96, 151906 (2010).
Lee, S. et al. Anomalously low electronic thermal conductivity in metallic vanadium dioxide. Science 355, 371–374 (2017).
Dahal, K. et al. Thermal conductivity of (VO2)1-xCux composites across the phase transition temperature. J. Appl. Phys. 121, 155103 (2017).
Strelcov, E. et al. Doping-based stabilization of the M2 phase in free-standing VO2 nanostructures at room temperature. Nano Lett. 12, 6198–6205 (2012).
Sohn, J. I. et al. Surface-stress-induced Mott transition and nature of associated spatial phase transition in single crystalline VO2 nanowires. Nano Lett. 9, 3392–3397 (2009).
Peierls, R. E. More Surprises In Theoretical Physics, Vol. 19 (Princeton University Press, 1991).
Goodenough, J. B. The two components of the crystallographic transition in VO2. J. Solid State Chem. 3, 490–500 (1971).
Liebsch, A., Ishida, H. & Bihlmayer, G. Coulomb correlations and orbital polarization in the metal-insulator transition of VO2. Phys. Rev. B 71, 085109 (2005).
Kim, S., Kim, K., Kang, C.-J. & Min, B. Correlation-assisted phonon softening and the orbital-selective Peierls transition in VO2. Phys. Rev. B 87, 195106 (2013).
Budai, J. D. et al. Metallization of vanadium dioxide driven by large phonon entropy. Nature 515, 535 (2014).
Eyert, V. The metal‐insulator transitions of VO2: a band theoretical approach. Ann. Phys. 11, 650–704 (2002).
de Groot, F. M., Fuggle, J. C., Thole, B. T. & Sawatzky, G. A. 2p x-ray absorption of 3d transition-metal compounds: an atomic multiplet description including the crystal field. Phys. Rev. B Condens. Matter 42, 5459 (1990).
Santos, I., Cazzaniga, M., Onida, G. & Colombo, L. Atomistic study of the structural and electronic properties of a-Si:H/c-Si interfaces. J. Phys. Condens Matter 26, 095001 (2014).
Lim, M., Jackson, T. A. & Anfinrud, P. A. Binding of CO to myoglobin from a heme pocket docking site to form nearly linear Fe-C-O. Science 269, 962–966 (1995).
Korotin, M. A., Skorikov, N. A. & Anisimov, V. I. Variation of orbital symmetry of the localized 3d1 electron of the V4+ ion upon the metal-insulator transition in VO2. The Physics of Metals and Metallography 94, 17–23 (2012).
Continenza, A., Massidda, S. & Posternak, M. Self-energy corrections in within a model scheme. Phys. Rev. B 60, 15699–15704 (1999).
Gatti, M., Bruneval, F., Olevano, V. & Reining, L. Understanding correlations in vanadium dioxide from first principles. Phys. Rev. Lett. 99, 266402 (2007).
Tomczak, J. M. & Biermann, S. Effective band structure of correlated materials: the case of VO2. J. Phys. Condens. Matter Inst. Phys. J. 19, 365206 (2007).
Eaglesham, D. J. et al. Erratum: “Equilibrium shape of Si” [Phys. Rev. Lett. 70, 1643 (1993)]. Phys. Rev. Lett. 72, 1392 (1994).
Kim, S., Kim, K., Kang, C. J. & Min, B. I. Correlation assisted phonon softenings and the Mott-Peierls transition in VO_2. Physics 87, 2497–2504 (2012).
Yao, T. et al. Understanding the nature of the kinetic process in a VO2 metal-insulator transition. Phys. Rev. Lett. 105, 226405 (2010).
Morrison, V. R. et al. A photoinduced metal-like phase of monoclinic VO2 revealed by ultrafast electron diffraction. Science 346, 445–448 (2014).
Li, Z. et al. Imaging metal-like monoclinic phase stabilized by surface coordination effect in vanadium dioxide nanobeam. Nat. Commun. 8, 15561 (2017).
Xu, Y. et al. Synthesis and properties of Mo and W ions co-doped porous nano-structured VO2 films by sol–gel process. J. Sol-Gel Sci. Technol. 64, 493–499 (2012).
Wu, Y. et al. Decoupling the lattice distortion and charge doping effects on the phase transition behavior of VO2 by titanium (Ti4+) doping. Sci. Rep. 5, 9328 (2015).
Shibuya, K., Kawasaki, M. & Tokura, Y. Metal-insulator transition in epitaxial V1−xWxO2 (0 ≤ x ≤ 0.33) thin films. Appl. Phys. Lett. 96, 022102 (2010).
Gu, Q. et al. Current-driven phase oscillation and domain-wall propagation in Wx V1-xO2 nanobeams. Nano Lett. 7, 363–366 (2007).
Rakotoniaina, J. et al. The thermochromic vanadium dioxide: I. Role of stresses and substitution on switching properties. J. Solid State Chem. 103, 81–94 (1993).
Asayesh-Ardakani, H. et al. Atomic origins of monoclinic-tetragonal (rutile) phase transition in doped VO2 nanowires. Nano Lett. 15, 7179–7188 (2015).
Brückner, W., Gerlach, U. & Thuss, B. Phase diagram of V1‐xAlxO2. Phys. Status Solidi (a) 40, K131–K134 (1977).
Marezio, M., McWhan, D. B., Remeika, J. P. & Dernier, P. D. Structural aspects of the metal-insulator transitions in Cr-doped VO2. Phys. Rev. B 5, 2541 (1972).
Booth, J. M. & Casey, P. S. Anisotropic structure deformation in the VO2 metal-insulator transition. Phys. Rev. Lett. 103, 086402 (2009).
Wei, J. et al. Hydrogen stabilization of metallic vanadium dioxide in single-crystal nanobeams. Nat. Nanotechnol. 7, 357–362 (2012).
Yoon, H. et al. Reversible phase modulation and hydrogen storage in multivalent VO2 epitaxial thin films. Nat. Mater. 15, 1113–1119 (2016).
Chen, Y. et al. Non-catalytic hydrogenation of VO2 in acid solution. Nat. Commun. 9, 818 (2018).
Filinchuk, Y. et al. In situ diffraction study of catalytic hydrogenation of VO2: stable phases and origins of metallicity. J. Am. Chem. Soc. 136, 8100–8109 (2014).
Teschner, D. et al. The roles of subsurface carbon and hydrogen in palladium-catalyzed alkyne hydrogenation. Science 320, 86–89 (2008).
Stefanovich, G., Pergament, A. & Stefanovich, D. Electrical switching and Mott transition in VO2. J. Phys. Condens. Matter 12, 8837 (2000).
Gopalakrishnan, G., Ruzmetov, D. & Ramanathan, S. On the triggering mechanism for the metal–insulator transition in thin film VO2 devices: electric field versus thermal effects. J. Mater. Sci. 44, 5345–5353 (2009).
Zhou, Y. et al. Voltage-triggered ultrafast phase transition in vanadium dioxide switches. IEEE Electron Device Lett. 34, 220–222 (2013).
Joushaghani, A. et al. Voltage-controlled switching and thermal effects in VO2 nano-gap junctions. Appl. Phys. Lett. 104, 221904 (2014).
Leroy, J. et al. High-speed metal-insulator transition in vanadium dioxide films induced by an electrical pulsed voltage over nano-gap electrodes. Appl. Phys. Lett. 100, 337 (2012).
Kim, H.-T. et al. Mechanism and observation of Mott transition in VO2-based two-and three-terminal devices. New J. Phys. 6, 52 (2004).
Aronov, A. & Kudinov, E. Phase transition in strong electron-phonon interaction. Sov. Phys. JETP 28, 704–709 (1969).
Chen, Y. et al. Free-standing SWNTs/VO2/Mica hierarchical films for high-performance thermochromic devices. Nano Energy 31, 144–151 (2017).
Sengupta, S. et al. Field-effect modulation of conductance in VO2 nanobeam transistors with HfO2 as the gate dielectric. Appl. Phys. Lett. 99, 650–R (2011).
Ruzmetov, D. et al. Three-terminal field effect devices utilizing thin film vanadium oxide as the channel layer. J. Appl. Phys. 107, 50 (2010).
Yajima, T., Nishimura, T. & Toriumi, A. Positive-bias gate-controlled metal–insulator transition in ultrathin VO2 channels with TiO2 gate dielectrics. Nat. Commun. 6, 10104 (2015).
Yang, Z., Zhou, Y. & Ramanathan, S. Studies on room-temperature electric-field effect in ionic-liquid gated VO2 three-terminal devices. J. Appl. Phys. 111, 114516 (2012).
Zhou, Y. & Ramanathan, S. Relaxation dynamics of ionic liquid-VO2 interfaces and influence in electric double-layer transistors. J. Appl. Phys. 111, 052905 (2012).
Sim, J. S., Zhou, Y. & Ramanathan, S. Suspended sub-50 nm vanadium dioxide membrane transistors: fabrication and ionic liquid gating studies. Nanoscale 4, 7056–7062 (2012).
Ji, H., Wei, J. & Natelson, D. Modulation of the electrical properties of VO2 nanobeams using an ionic liquid as a gating medium. Nano Lett. 12, 2988–2992 (2012).
Lu, N. et al. Electric-field control of tri-state phase transformation with a selective dual-ion switch. Nature 546, 124–128 (2017).
Sasaki, T., Ueda, H., Kanki, T. & Tanaka, H. Electrochemical gating-induced reversible and drastic resistance switching in VO2 nanowires. Sci. Rep. 5, 17080 (2015).
Kanki, T., Sasaki, T. & Tanaka, H. Electrochemical gating-induced hydrogenation in VO2 nanowires at room temperature. ECS Trans. 75, 103–109 (2016).
Zhou, Y. et al. Control of emergent properties at a correlated oxide interface with graphene. Nano Letters 15, 1627–1634 (2015).
Jeong, J. et al. Giant reversible, facet-dependent, structural changes in a correlated-electron insulator induced by ionic liquid gating. Proc. Natl Acad. Sci. USA 112, 1013–1018 (2015).
Nakano, M. et al. Distinct substrate effect on the reversibility of the metal–insulator transitions in electrolyte‐gated VO2 thin films. Adv. Electron. Mater. 1, 321–330 (2015).
Chen, S. et al. The dynamic phase transition modulation of ion‐liquid gating VO2 thin film: formation, diffusion, and recovery of oxygen vacancies. Adv. Funct. Mater. 26, 3532–3541 (2016).
Peng, X. et al. Efficient and hysteresis-free field effect modulation of ambipolarly doped vanadium dioxide nanowires. Phys. Rev. Appl. 5, 054008 (2016).
Becker, M. et al. Femtosecond laser excitation dynamics of the semiconductor‐metal phase transition in VO2. Appl. Phys. Lett. 79, 2404–2408 (1996).
Atwater, H. A., Pryce, I. M. & Briggs, R. M. Compact silicon photonic waveguide modulator based on the vanadium dioxide metal-insulator phase transition. Opt. Express 18, 11192 (2010).
Roach, W. R. & Balberg, I. Optical induction and detection of fast phase transition in VO2. Solid State Commun. 9, 551–555 (1971).
Cavalleri, A. et al. Femtosecond structural dynamics in VO2 during an ultrafast solid-solid phase transition. Phys. Rev. Lett. 87, 237401 (2001).
Tang, Y. L. et al. Measurement-device-independent quantum key distribution over 200 km. Phys. Rev. Lett. 113, 190501 (2014).
Wall, S. et al. Tracking the evolution of electronic and structural properties of VO2 during the ultrafast photoinduced insulator-metal transition. Phys. Rev. B 87, 115126 (2013).
Park, J. H. et al. Measurement of a solid-state triple point at the metal-insulator transition in VO2. Nature 500, 431–434 (2013).
Cao, J. et al. Strain engineering and one-dimensional organization of metal–insulator domains in single-crystal vanadium dioxide beams. Nat. Nanotechnol. 4, 732–737 (2009).
Khomskii, D. & Sawatzky, G. Interplay between spin, charge and orbital degrees of freedom in magnetic oxides. Solid State Commun. 102, 87–99 (1997).
Tokura, Y. & Nagaosa, N. Orbital physics in transition-metal oxides. Science 288, 462–468 (2000).
Fiebig, M., Miyano, K., Tomioka, Y. & Tokura, Y. Visualization of the local insulator-metal transition in Pr0.7Ca0.3MnO3. Science 280, 1925–1928 (1998).
Wu, J. et al. Strain-induced self organization of metal− insulator domains in single-crystalline VO2 nanobeams. Nano Lett. 6, 2313–2317 (2006).
Fan, L. L. et al. Strain dynamics of ultrathin VO2 film grown on TiO2 (001) and the associated phase transition modulation. Nano Lett. 14, 4036–4043 (2014).
Nagashima, K., Yanagida, T., Tanaka, H. & Kawai, T. Stress relaxation effect on transport properties of strained vanadium dioxide epitaxial thin films. Phys. Rev. B 74, 172106 (2006).
Lee, D. et al. Sharpened VO2 phase transition via controlled release of epitaxial strain. Nano Lett 17, 5614–5619 (2017).
Yang, T.-H. et al. Semiconductor-metal transition characteristics of VO2 thin films grown on c-and r-sapphire substrates. J. Appl. Phys. 107, 053514 (2010).
Aetukuri, N. B. et al. Control of the metal-insulator transition in vanadium dioxide by modifying orbital occupancy. Nat. Phys. 9, 661–666 (2013).
Liao, F. et al. Ultrafast response flexible breath sensor based on vanadium dioxide. J. Breath Res. 11, 036002 (2017).
Zhao, X. et al. Flexible, stretchable and wearable multifunctional sensor array as artificial electronic skin for static and dynamic strain mapping. Adv. Electron. Mater. 1, 1500142 (2015).
Wegkamp, D. & Stähler, J. Ultrafast dynamics during the photoinduced phase transition in VO2. Prog. Surf. Sci. 90, 464–502 (2015).
Eyert, V. VO2: a novel view from band theory. Phys. Rev. Lett. 107, 016401 (2011).
Wegkamp, D. et al. Instantaneous band gap collapse in photoexcited monoclinic VO2 due to photocarrier doping. Phys. Rev. Lett. 113, 216401 (2014).
Zhu, Z. & Schwingenschlögl, U. Comprehensive picture of VO2 from band theory. Phys. Rev. B 86, 6709–6717 (2012).
Acknowledgements
This study was financially supported by the National Natural Science Foundation of China (NSFC, No. 51572284). X. Cao wants to thank the “Youth Innovation Promotion Association, Chinese Academy of Sciences” (No. 2018288), the Science Foundation for Youth Scholar of State Key Laboratory of High Performance Ceramics and Superfine Microstructures (No. SKL201703), and the key research and development plan of Anhui province (1804a09020061).
Author information
Authors and Affiliations
Contributions
Z.S. wrote the whole manuscript under the supervision of Prof. X.C. X.C. guided this work and designed the plan of the whole review. H.L. and P.J. gave much discussion about the details and development direction.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shao, Z., Cao, X., Luo, H. et al. Recent progress in the phase-transition mechanism and modulation of vanadium dioxide materials. NPG Asia Mater 10, 581–605 (2018). https://doi.org/10.1038/s41427-018-0061-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41427-018-0061-2
This article is cited by
-
Local gate control of Mott metal-insulator transition in a 2D metal-organic framework
Nature Communications (2024)
-
Polarized Raman mapping and phase-transition by CW excitation for fast purely optical characterization of VO2 thin films
Scientific Reports (2024)
-
Nanoscale optical nonreciprocity with nonlinear metasurfaces
Nature Communications (2024)
-
Metal-insulator transition effect on Graphene/VO\(_\text {2}\) heterostructure via temperature-dependent Raman spectroscopy and resistivity measurement
Scientific Reports (2024)
-
All-optical seeding of a light-induced phase transition with correlated disorder
Nature Physics (2024)