Abstract
A recent development in the genetic architecture of schizophrenia suggested that an omnigenic model may underlie the risk for this disorder. The aim of our study was to use polygenic profile scoring to quantitatively assess whether a number of experimentally derived sets would contribute to the disorder above and beyond the omnigenic effect. Using the PGC2 secondary analysis schizophrenia case-control cohort (N = 29,125 cases and 34,836 controls), a robust polygenic signal was observed from gene sets based on TCF4, FMR1, upregulation from MIR137 and downregulation from CHD8. Additional analyses revealed a constant floor effect in the amount of variance explained, consistent with the omnigenic model. Thus, we report that putative core gene sets showed a significant effect above and beyond the floor effect that might be linked with the underlying omnigenic background. In addition, we demonstrate a method to quantify the contribution of specific gene sets within the omnigenic context.
Similar content being viewed by others
Introduction
Schizophrenia is a highly heritable disorder showing complex genomic architecture. Genome-wide association studies (GWASs) have been used to identify the common variants contributing to the risk of disease and measure their collective effect. A recent schizophrenia GWAS [1] identified over a hundred common single-nucleotide polymorphisms (SNPs) at genome-wide significance levels, though the effect of each SNP on its own was modest.
The underpinning architecture of schizophrenia remains unclear [2]. Several methods have been applied to capture cumulative common variation that might confer vulnerability, including polygenic risk scores (PRSs) [3, 4]. PRSs use the coefficients derived from a discovery GWAS as weights for each SNP allele in order to calculate an overall risk score for each individual in an independent sample. PRSs are capable of explaining some proportion of overall variance in liability.
In order to identify the underlying biological pathways, gene-set enrichment analyses have been conducted using categories defined by gene ontology or by biochemical interaction with the products of high-risk genes [5]. Methods such as MAGMA [6], INRICH [7] and ALIGATOR [8] have allowed the in-depth exploration of GWAS results in terms of finding biochemical pathway enrichment, and have been crucial in expanding our understanding of potential underlying mechanisms of complex traits. However, despite their prominence in GWAS [9, 10] and exome-sequencing studies [11], these analyses do not estimate the contribution of these gene sets to the amount of variance explained; instead, they state whether the gene set is more enriched, in terms of GWAS p-values, than expected by chance.
A recent paper [12] suggested that SNPs in all genes expressed in the relevant tissue (e.g., brain in schizophrenia) make a contribution to heritability and polygenic risk. Within that context there are two types of genes, core and peripheral, that confer risk. Genes identified in GWASs or rare-variant studies may be core genes that serve as the basis of developing networks used to identify peripheral genes.
Our study aimed to quantitatively assess whether specific gene sets, centred on putative core genes, make a larger-than-expected contribution to polygenic risk. We focused on eight gene sets, six of which are centred on genes previously implicated in schizophrenia risk. We hypothesized that these sets would be associated with schizophrenia case-control status at a greater-than-expected level. The remaining two gene sets were associated with cancer and cardiac disease (CD). The rationale behind the choice of each included gene set is presented below. For comparison, we examined the behaviour of the PRSs under H0. Finally, to investigate the omnigenic hypothesis on schizophrenia risk [12], we generated linkage disequilibrium (LD) independent random genic and non-genic SNP sets of equal size to the gene sets investigated. Comparison of these sets to the putative core gene sets may produce a better estimate of their contribution under the omnigenic model.
The six schizophrenia core gene-associated (SCGA) target gene sets were selected from recent studies [13,14,15,16] based on transcriptional or molecular interactions with schizophrenia putative core genes. SNPs in the gene transcription factor 4 (TCF4) are genome-wide significantly associated with risk for schizophrenia [1, 17], and haploinsufficiency of this gene causes Pitt–Hopkins syndrome, associated with severe cognitive deficits [18, 19] and risk for psychosis [20]. The TCF4 gene set was created on the basis of the differential expression of genes in neuroblastoma cells after knockdown of TCF4 [13]. A total of 1052 autosomal genes (5652 SNPs) demonstrating differential expression were included in the gene set. FMR1 (Fragile X metal retardation 1) is a gene coding for FMRP (fragile X mental retardation protein), whose loss of function results in fragile X syndrome [21], often co-morbid with autism spectrum disorders. FMR1 mutations have been linked with cognitive impairment and earlier age of onset in schizophrenia [22]. The FMRP gene set was created on the basis of functional gene sets based on developmental expression of genes contingent on FMRP expression [14]. All four gene subsets were combined into one gene set containing 680 autosomal genes (5833 SNPs). MIR137 is a microRNA with high levels of expression in the brain and neural stem cells [23]. Transcriptional targets of MIR137, such as ZNF804A and CACNA1C, as well as the gene itself, have been implicated with schizophrenia [17, 24, 25]. The third and fourth gene sets were chosen on the basis of the work of Hill et al. [15], where two gene sets were generated from upregulated (817 genes and 7796 SNPs) and downregulated (761 genes and 8533 SNPs) genes after overexpression of MIR137 in neural progenitor cells in vitro. CHD8 (Chromodomain Helicase DNA Binding Protein 8) codes for a DNA helicase that suppresses gene expression by affecting chromatin restructure, and is a significant contributor to autism susceptibility [26] and CHARGE syndrome (a congenital deaf–blindness syndrome) through its interaction with CHD7 [27]. Rare variants in CHD8 may contribute to schizophrenia risk [28]. The final neural gene sets were generated from the findings of Sugathan et al. [16], where CHD8 reduction in neural progenitor cells led to the creation of two gene sets, one of upregulated (1140 genes and 8807 SNPs) and the other of downregulated (616 genes and 4986 SNPs) genes. For the latter two gene sets, the decision to split them into downregulated and upregulated gene sets was based on reports [15, 16] describing a more pronounced response under one of the conditions. Additionally, we selected two gene sets that were related to CD and cancer, drawn from the CD database (http://www.bioguo.org/CADgene/) and the Atlas of Genetics and Cytogenetics in Oncology and Haematology (atlasgeneticsoncology.org). Those gene sets had 534 and 459 genes, respectively (with 8078 and 7316 SNPs). The rationale for using these non-schizophrenia gene sets was mainly to serve as null sets of roughly equal size to the SCGA gene sets.
Materials and methods
The Schizophrenia Working Group of the Psychiatric Genomics Consortium 2 case-control GWASs
Sample composition and selection is described in detail in Ripke et al. [1]. In brief, cases were selected based on a diagnosis of either schizophrenia or schizoaffective disorder, as the two disorders tend to aggregate together in family studies [29] and there is a low inter-rater reliability across the two groups on the basis of their initial diagnosis [30]. The quality of diagnosis for cases was assessed through a questionnaire examining quality control and diagnosis procedures [1]. Studies with different case ascertainment procedures were included in the final sample [31]. Two of the studies included cases that were selected on the basis of clozapine prescription and a prior diagnosis of treatment-resistant schizophrenia [32]. In total, 39 different studies were included. The sample was composed of 29,125 cases and 34,836 controls of European ancestry. There were 36,318 males, 22,061 females and 5582 participants with no sex information. Details of subject composition for each individual study and how these were collected, as well as details about ethics committee review and written informed consent, can be found in Ripke et al. [1] and in the appendix (Supplementary Table S1). Genotypes were imputed using the 1000 Genomes Project dataset (August 2012, 30,069,288 variants, release “v3.macGT1”) as a reference for the imputation process, through the use of IMPUTE2/SHAPEIT [33]. Quality control excluded the following: SNP missingness < 0.05 (before sample removal), subject missingness < 0.02, autosomal heterozygosity deviation (|Fhet| < 0.2), SNP missingness < 0.02 (after sample removal), difference in SNP missingness between cases and controls < 0.02, and SNP Hardy–Weinberg equilibrium (p-value > 10−6 in controls or p-value > 10−10 in cases).
Leave-one-out (LOO) PRS analysis
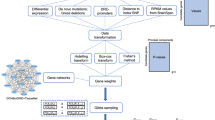
Two datasets were created for each of the 39 studies: one with every dataset but the held-out set, serving as the training set; and the other with the held-out set, serving as the independent testing set. For each study, a GWAS was performed in the training set to calculate the p-value and ln(odds ratio) of each individual SNP (Fig. 1a). To confirm that SNPs in the training set were coding the same reference allele as the risk allele in the test study, we coded all SNPs as risk by selecting the allele with OR > 1. Afterwards, PRSs were created for nine different p-value cut-off thresholds (0.0001, 0.001, 0.01, 0.05, 0.10, 0.20, 0.30, 0.40 and 0.50). These were generated for the training set to reduce the need of correction for multiple testing on the held-out test set. A logistic regression model was fitted for each of these nine scores in each of the 39 training sets that included 38 studies, including covariates (count of valid genotypes, principle components and study indicators) [1]. In each study, the largest test statistic from the nine scores in the training set was used to select the single PRS to be tested on each of the 39 held-out test sets (Fig. 1a).
a Leave-one-out cross-validation process. Example of leave-one-out cross-validation process for a sample containing four datasets. The same process was followed with the 39 PGC datasets. b Flowchart for polygenic score generation in each leave-one-out Iteration. Flowchart of the process followed in each iteration of the leave-one-out cross-validation. PRS input files are the polygenic scoring file and the individual SNP p-value file. PRS polygenic risk score; LRT likelihood ratio test
Statistical analysis
All analyses were performed in PLINK 1.90 [34] for PRS generation and genetic data manipulation, and in R 3.2.4 for the generation of regression models. The R package fmsb [35] was used to calculate Nagelkerke’s R2. Note that the use of R2 here is to indicate the percentage of variation in case status explained; the use of r2 below indicates the LD or correlation between alleles at two SNPs. MetaP (Dongliang G, Duke Institute for Genome Sciences and Policy, NC, USA) was used to perform Stouffer’s Z p-value meta-analysis [36]. The gene sets described above included only the autosomal SNPs. LD pruned the SNP discovery set in PLINK using a sliding window of 50 SNPs, a sliding step of 5 SNPs and an r2 threshold of inclusion at 0.25. For the regression analysis, the original [1] principal components were used to control for population stratification, adding the study indicators as covariates. Finally, we used likelihood ratio tests between nested regression models and calculated the Nagelkerke R2 and the p-value for the PRS in each of the 39 held-out test datasets.
Meta-analysis
To estimate the significance of the results in the overall sample, we performed a meta-analysis of the 39 results from the test sets only, using Stouffer’s Z p-value in metaP, also accounting for directionality of effect and sample size. Because each training set would have different ln(odds ratios) and p-values, each PRS was different; we thus combined p-values. For the Nagelkerke nested R2 values, we provided the median, interquartile range and range from the held-out test sets.
Simulation and validation studies
We performed two additional studies to examine the methodology used and the influence of genic versus non-genic SNPs, as genic SNPs might produce inflated results [37]. The first analysis was a standard experiment-wise randomization test on the TCF4 gene set, consisting of permuting the phenotype 100 times and rerunning the entire experimental pipeline, leaving a single study out at a time, on these randomly generated phenotypes (Supplementary Fig. 1). If the pipeline is robust to type I error, 5% of these permuted experiment-wise results should show a significant result at α = 0.05. For the second analysis, we generated 50 random subsets of genic SNPs, defined as SNPs found within genes, 5 kb upstream of genes or 1 kb downstream of genes, of a mean size of 5000 SNPs and an equal number of non-genic SNP subsets, defined as SNPs not included in the genic subset. All SNPs were pruned at an R2 cutoff of 0.01 beforehand to make sure that only independent SNPs were selected. We ran the pipeline with all methods as previously outlined to establish if there was an omnigenic effect consistently present across the random sets and if there was a further systematic enrichment of the genic SNPs sets.
Results
Gene set characteristics
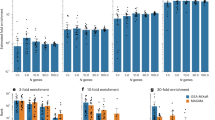
Initially, we investigated if there was any overlap among the SCGA and control gene sets. We found little overlap among any gene sets (Fig. 2). In the SCGA gene sets, there were no overlapping genes in all four sets, and no two sets overlapped by more than 3% of the total genes shared. The CD and cancer gene sets showed minimal overlap between them (31 genes, 2.8%). Finally, the SCGA and non-SCGA sets had an overlap of 261 genes (5.3%). The biggest groups among overlapping genes were protein-binding genes, signalling molecule genes and receptor molecule genes.
Overlap of gene sets. a Neuronal gene sets. b Non-neuronal gene sets. c Combination of a and b. Percentages in the graph indicate the percentage of the total genes found in each overlapping segment. MIR137 and CHD8 indicate all the genes for both the down- and the upregulated gene sets as there was no overlap between the two
PRS analysis
TCF4 gene-set-weighted scores were the most strongly associated in the meta-analysis (Stouffer’s Z p-value = 1.18 × 10−46; Fig. 2). This particular gene set was one where most of the individual studies, as independent test sets in the LOO, were significant (29/39), showing evidence for association at p-value < 0.05 (uncorrected, as only one score was tested in each of the held-out test sets; Table 1). This gene set explained the highest percentage of variability among the studies described (Nagelkerke R2 = 0.6%; Fig. 3). In the original PGC2 study [1], TCF4 was GWAS-significantly associated with schizophrenia, and thus might have been driving the results. To test this, 12 SNPs within TCF4 were removed and the analysis was repeated, with results at the same level of significance (Stouffer’s Z p-value = 4.28 × 10−40) and effect size (Nagelkerke R2 = 0.6%). FMRP gene-set-weighted scores were also significant (Stouffer’s Z p-value = 1.66 × 10−33), with 23/39 individual independent test set results showing evidence for association; it explained 0.43% of the schizophrenia case-control status. For the two MIR137-regulated gene sets, we observed significant association with schizophrenia with Stouffer’s Z p-value = 3.28 × 10−23 for the upregulated gene set, and Stouffer’s Z p-value = 1.06 × 10−11 for the downregulated gene set, explaining 0.4% and 0.28%, respectively, of schizophrenia case status. For the CHD8 gene set PRSs, the downregulated gene set was significant (Stouffer’s Z p-value = 1.91 × 10−33) and explained 0.37% of the variability. The scores created from the upregulated genes were also significant (Stouffer’s Z p-value = 1.73 × 10−11), but only a small number of individual held-out test sets were individually significant (7/39) and the overall effect explained 0.2% of the variability.
R2 and p-values from meta-analysis of all gene sets. Numbers on top of the bars denote the meta-analysed Stouffer’s Z p-value for the gene set and the number of polygenic scores that were significant in independent, held-out test studies. For the genic and non-genic sets, the statistics represent the median of 50 sets; the line above the box represents the range of these sets for the 50 iterations of each. The final box is the median results for 100 permuted phenotype iterations
Gene sets created from the non-SCGA sources were weakly, but still statistically significantly, associated with the outcome (Stouffer’s Z p-value = 2.14 × 10−4 and 1.67 × 10−3, respectively). Six and four out of the 39 polygenic scores were significant at p-value < 0.05 (uncorrected) in those analyses, respectively. To examine the distribution of p-values across all of the gene sets investigated, we created p-value bins corresponding to deciles under H0, where p-values are distributed ~U (0,1). For all the gene sets investigated, there was an increased proportion of SNPs in the top 10% bin for all gene sets, consistent with the quantile–quantile (Q–Q) plot from the PGC2 mega-analysis [1] and our own Q–Q plot demonstrating a deviation of the distribution of p-values from expected under H0 (Supplementary Fig. 2).
A genome-wide PRS was generated (3,848,785 SNPs) with a median nested Nagelkerke R2 value of 0.24. If each SNP contributed equally to the score, then the results for the pathways of interest should only be able to explain roughly between 0.03% (0.24/3848785*4986, for CHD8 downregulated) and 0.055% (0.24/3848785*8807, for CHD8 upregulated). It is important to note that these results were for the 39 studies without pruning, and therefore not directly comparable to the ones that were generated with the LOO process.
Simulation and validation studies
In the simulation study that was performed, for 100 runs with permuted phenotypes, the type I error rate at α = 0.05 was as expected under H0, with 4 out of 100 having a Stouffer’s Z p-value value of less than 0.05 (i.e. type I error of 4%). In the examination of the omnigenic effect and the possible additional effect attributable to genic SNPs, 50 random subsets of 5000 independent (with LD < 0.25) genic and non-genic SNPs were generated, and the same analytical protocol described previously was implemented. On average, all sets of SNPs that were tested had a level of significance ranging from 10−2 to 10−7, with no individual set exceeding the significance of the SCGA sets. Genic sets were consistently, but only slightly, more significant than non-genic sets (median Stouffer’s Z p-value = 1.06 × 10−4 versus 2.54 × 10−3). The nested Nagelkerke R2 values were also higher in the genic set with a median value of 0.0021 versus 0.0016 for the non-genic set.
We examined our SCGA gene sets for enrichment in genes specifically expressed in nervous system tissues or for broadly expressed genes. The omnigenic model suggests that there will be enrichment in gene sets associated with schizophrenia. Results from that analysis (Supplementary Table S2) indicate an enrichment of broad terms for most of the gene sets under examination, with the exception of the FMRP gene set, which showed an excess enrichment for neuron-specific functions and more specifically nervous system development (p-value = 3.36 × 10−60) and generation of neurons (p-value = 6.97 × 10−44). For the non-SCGA gene sets, there was an enrichment for DNA regulation elements (cancer) and response to stressors (CD).
Discussion
PRSs were used to investigate whether potential core gene sets played a significant role in the omnigenic model of schizophrenia. There was significant heterogeneity among the gene sets, with the TCF4 gene set, the FMRP gene set, the gene set upregulated in the presence of excess MIR137 and the gene set downregulated in the absence of CHD8 shown to be associated with schizophrenia. In contrast, the apparently significant effects that were observed in the control gene sets (cancer and CD), as well as the gene set downregulated in the presence of excess MIR137 and the gene set upregulated in the absence of CHD8, were not higher than a floor effect observed with random sets of genic SNPs and non-genic SNPs and could be attributable to an omnigenic or highly polygenic background [12]. Our results were not driven by gene sizes within each gene set (Supplementary Table S3).
Among the investigated sets, the TCF4 gene set was the most strongly associated with schizophrenia, with a Stouffer’s Z p-value of 1.18 × 10−46. The nested R2 effect observed was three times that of any set of random SNPs of the same size. The result retained its significance and magnitude of effect size even after removing SNPs within the core gene TCF4, indicating that the observed relationship exists between peripheral genes of the gene set and the phenotype above the effect that TCF4 might exert as a core gene. There is consistent evidence for the role of TCF4 in schizophrenia [1, 17]. Additionally, due to the nature of SNPs implicated (non-coding genetic elements), the pathway of genes influenced by TCF4 expression [38] might also be potentially involved in the common polygenic background of the disorder.
The FMRP gene set was also significantly associated with schizophrenia. FMRP has primarily been implicated in autism spectrum disorders. There are commonalities among both the clinical features and genomics of major psychiatric disorders and a recent cross-disorder mega-analysis GWAS [39] that indicated that common variation predisposing to mental illnesses might be shared to some degree among major psychiatric disorders. Additional evidence of the involvement of FMRP targets to schizophrenia can be observed from rare variant studies that have consistently implicated FMRP pathways with schizophrenia [40,41,42].
In the two MIR137 gene sets, there was a positive effect only on the gene set that was upregulated after MIR137 over expression. The downregulated gene set, although statistically significant, did not show an effect stronger than what would be expected by the omnigenic model using randomly selected genic SNPs. This result is consistent with findings of other studies of MIR137 expression indicating that upregulation of the gene is linked with pathways implicated in psychosis (such as the major histocompatibility complex) [43] and with enrichment analyses of MIR137 potential target pathways [44].
Of CHD8 gene sets, only the downregulated gene set showed evidence for significant association. CHD8 has not previously been centrally implicated in psychosis as it is associated with a congenital disorder (CHARGE syndrome) and linked to autism [26]. However, there is a reasonable argument to be made on the basis of common susceptibility to mental disorders that genes central to other major mental disorders might also affect schizophrenia. There has been recent evidence on rare variants in the gene [28, 45] being implicated in psychosis, which adds to the notion of the cross-disorder nature of CHD8 pathways. The downregulated gene set that was significantly associated with schizophrenia in the present study was also the one that Sugathan et al. [16] reported to be significantly enriched in autism.
In addition to the above findings, a systematic floor effect in polygenic scores was observed. We propose that this observation is consistent with predictions that would be made based on the recently proposed omnigenic model of complex traits such as schizophrenia. This model states that most genes expressed in cells that are relevant to the biology of an illness contribute to heritability and PRSs because of the likely interaction of multiple signalling pathways within cells that support their biological functions. In the light of this omnigenic hypothesis [12], implicating a greater number of SNPs than the ordinary polygenic model would suggest, our results support the hypothesis by demonstrating a weak polygenic effect extant in every random subset of genes. This omnigenic effect is also supported by Supplementary Fig. 2, which demonstrates an overall increase in SNP test statistics versus expected values, as well as the Q–Q plot in the original PGC2 report [1] that also showed a very similar effect across an increased number of observations. Enrichment analysis indicated an enrichment for broadly expressed genes, which also corroborates the principle finding of the omnigenic model [12] for schizophrenia. Additionally, we report that genic SNP sets seemed to explain slightly more variation than their non-genic counterparts. This indicates that studies implementing a pathway stratagem should be mindful of both effects when assessing if a gene set explains more variation than a random subset of genic or non-genic SNPs.
This study showed that several of the target putative core gene-sets investigated were highly significantly associated with schizophrenia, with the strongest effect being observed for the TCF4 core gene set. Even though most of the genes in these sets are not associated with risk in current GWAS datasets, they may be part of networks of genes that underlie common mechanisms for schizophrenia. These findings strongly indicate that, despite a very widespread, possibly even omnigenic contribution to risk, it is possible to identify subsets of genes making relatively larger contributions—putative core genes—which may implicate specific biochemical pathways or molecular processes with selectively greater roles in pathogenesis.
References
Ripke S, Neale BM, Corvin A, Walters JT, Farh KH, Holmans PA, et al. Biological insights from 108 schizophrenia-associated genetic loci. Nature. 2014;511:421–7.
Mitchell KJ. The genetics of neurodevelopmental disorders. Hoboken, NJ, USA: John Wiley & Sons; 2015.
Purcell S, Wray N, Stone J, Visscher P, O’Donovan M, Sullivan P, et al. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature. 2009;460:748–52.
Nicodemus KK, Hargreaves A, Morris D, Anney R, Gill M, Corvin A, et al. Variability in working memory performance explained by epistasis vs olygenic scores in the ZNF804A pathway. JAMA Psychiatry. 2014;71:778.
Subramanian A, Tamayo P, Mootha VK, Mukherjee S, Ebert BL, Gillette MA, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci. 2005;102:15545–50.
de Leeuw C, Mooij J, Heskes T, Posthuma D. MAGMA: generalized gene-set analysis of GWAS data. PLOS Comput Biol. 2015;11:e1004219.
Lee P, O’Dushlaine C, Thomas B, Purcell S. INRICH: interval-based enrichment analysis for genome-wide association studies. Bioinformatics. 2012;28:1797–9.
Holmans P, Green E, Pahwa J, Ferreira M, Purcell S, Sklar P, et al. Gene ontology analysis of GWA study data sets provides insights into the biology of bipolar disorder. Am J Hum Genet. 2009;85:13–24.
O’Dushlaine C, Rossin L, Lee PH, Duncan L, Parikshak NN, Newhouse S, et al. Psychiatric genome-wide association study analyses implicate neuronal, immune and histone pathways. Nat Neurosci. 2015;18:199–209.
Pouget JG, Gonçalves VF, Spain SL, Finucane HK, Raychaudhuri S, Kennedy JL, et al. Genome-wide association studies suggest limited immune gene enrichment in schizophrenia compared to 5 autoimmune diseases. Schizophr Bull. 2016;42:1176–84.
Curtis D. Pathway analysis of whole exome sequence data provides further support for the involvement of histone modification in the aetiology of schizophrenia. Psychiatr Genet. 2016;26:223–7.
Boyle EA, Li YI, Pritchard JK. An expanded view of complex traits: from polygenic to omnigenic. Cell. 2017;169:1177–86.
Forrest MP, Waite AJ, Martin-Rendon E, Blake DJ. Knockdown of human TCF4 affects multiple signaling pathways involved in cell survival, epithelial to mesenchymal transition and neuronal differentiation. PLoS ONE. 2013;8:e73169.
Steinberg J, Webber C. The roles of FMRP-Regulated genes in autism spectrum disorder: single- and multiple-hit genetic Etiologies. Am J Hum Genet. 2013;93:825–39.
Hill MJ, Donocik JG, Nuamah RA, Mein CA, Sainz-Fuertes R, Bray NJ. Transcriptional consequences of schizophrenia candidate MIR137 manipulation in human neural progenitor cells. Schizophr Res. 2014;153:225–30.
Sugathan A, Biagioli M, Golzio C, Erdin S, Blumenthal I, Manavalan P, et al. CHD8 regulates neurodevelopmental pathways associated with autism spectrum disorder in neural progenitors. Proc Natl Acad Sci. 2014;111:E4468–77.
Ripke S, Sanders AR, Kendler KS, Levinson DF, Sklar P, Holmans PA, et al. Genome-wide association study identifies five new schizophrenia loci. Nat Genet. 2011;43:969–76.
Amiel J, Rio M, de Pontual L, Redon R, Malan V, Boddaert N, et al. Mutations in TCF4, encoding a class I basic helix-loop-helix transcription factor, are responsible for Pitt–Hopkins syndrome, a severe epileptic encephalopathy associated with autonomic dysfunction. Am J Hum Genet. 2007;80:988–93.
Sweatt JD. Pitt–Hopkins syndrome: intellectual disability due to loss of TCF4-regulated gene transcription. Exp Mol Med. 2013;45:e21.
Stefansson H, Ophoff R, Steinberg S, Andreassen O, Cichon S, Rujescu D, et al. Common variants conferring risk of schizophrenia. Nature. 2009;460:744–7.
Verheij C, Bakker CE, de Graaff E, Keulemans J, Willemsen R, Verkerk AJ, et al. Characterization and localization of the FMR-1 gene product associated with fragile X syndrome. Nature. 1993;363:722–4.
Kovács T, Kelemen O, Kéri S. Decreased fragile X mental retardation protein (FMRP) is associated with lower IQ and earlier illness onset in patients with schizophrenia. Psychiatry Res. 2013;210:690–3.
Guella I, Sequeira A, Rollins B, Morgan L, Torri F, van Erp TGM, et al. Analysis of MIR137 expression and rs1625579 in dorsolateral prefrontal cortex. J Psychiatr Res. 2013;47:1215–21.
Kim AH, Parker EK, Williamson V, McMichael GO, Fanous AH, Vladimirov VI. Experimental validation of candidate schizophrenia gene ZNF804A as target for hsa-MIR137. Schizophr Res. 2012;141:60–4.
Kwon E, Wang W, Tsai LH. Validation of schizophrenia-associated genes CSMD1, C10orf26, CACNA1C and TCF4 as MIR137 targets. Mol Psychiatry. 2011;18:11–2.
Wilkinson B, Grepo N, Thompson BL, Kim J, Wang K, Evgrafov OV, et al. The autism-associated gene chromodomain helicase DNA-binding protein 8 (CHD8) regulates noncoding RNAs and autism-related genes. Transl Psychiatry. 2015;5:e568.
Batsukh T, Pieper L, Koszucka AM, von Velsen N, Hoyer-Fender S, Elbracht M, et al. CHD8 interacts with CHD7, a protein which is mutated in CHARGE syndrome. Hum Mol Genet. 2010;19:2858–66.
Kimura H, Wang C, Ishizuka K, Xing J, Takasaki Y, Kushima I, et al. Identification of a rare variant in CHD8 that contributes to schizophrenia and autism spectrum disorder susceptibility. Schizophr Res. 2016;178:104–6.
Kendler K, Diehl S. The genetics of schizophrenia: a current, genetic-epidemiologic perspective. Schizophr Bull. 1993;19:261–85.
Faraone S, Blehar M, Pepple J, Moldin S, Norton J, Nurnberger J, et al. Diagnostic accuracy and confusability analyses: an application to the diagnostic interview for genetic studies. Psychol Med. 1996;26:401–10.
Hamshere ML, Walters JTR, Smith R, Richards AL, Green E, Grozeva D, et al. Genome-wide significant associations in schizophrenia to ITIH3/4, CACNA1C and SDCCAG8, and extensive replication of associations reported by the schizophrenia PGC. Mol Psychiatry. 2012;18:708–12.
Ripke S, O’Dushlaine C, Chambert K, Moran JL, Kähler AK, Akterin S, et al. Genome-wide association analysis identifies 13 new risk loci for schizophrenia. Nat Genet. 2013;45:1150–9.
Howie B, Marchini J, Stephens M, Chakravarti A. Genotype imputation with thousands of genomes. G3 (Bethesda). 2011;1:457–70.
Chang CC, Chow CC, Tellier LC, Vattikuti S, Purcell SM, Lee JJ. Second-generation PLINK: rising to the challenge of larger and richer datasets. GigaScience. 2015;4:7.
Nakazawa M Fmsb: functions for medical statistics book with some DemographicData. 2015. https://CRAN.R-project.org/package=fmsb. Accessed 20 Aug 2017.
Stouffer SA, DeVinney LC, Suchmen EA. The American soldier: adjustment during army life. USA: Military Affairs/Aerospace Historian; 1949.
Schork AJ, Thompson WK, Pham P, Torkamani A, Roddey JC, Sullivan PF, et al. All SNPs are not created equal: genome-wide association studies reveal a consistent pattern of enrichment among functionally annotated SNPs. PLoS Genet. 2013;9:e1003449.
Harrison PJ. Recent genetic findings in schizophrenia and their therapeutic relevance. J Psychopharmacol. 2014;29:85–96.
Cross-Disorder Group of the Psychiatric Genomics Consortium. Identification of risk loci with shared effects on five major psychiatric disorders: a genome-wide analysis. Lancet. 2013;381:1371–9.
Purcell SM, Moran JL, Fromer M, Ruderfer D, Solovieff N, Roussos P, et al. A polygenic burden of rare disruptive mutations in schizophrenia. Nature. 2014;506:185–90.
Fromer M, Pocklington AJ, Kavanagh DH, Williams HJ, Dwyer S, Gormley P, et al. De novo mutations in schizophrenia implicate synaptic networks. Nature. 2014;506:179–84.
Richards AL, Leonenko G, Walters JT, Kavanagh DH, Rees EG, Evans A, et al. Exome arrays capture polygenic rare variant contributions to schizophrenia. Hum Mol Genet. 2016;25:1001–7.
Collins AL, Kim Y, Bloom RJ, Kelada SN, Sethupathy P, Sullivan PF. Transcriptional targets of the schizophrenia risk gene MIR137. Transl Psychiatry. 2014;4:404.
Wright C, Calhoun VD, Ehrlich S, Wang L, Turner JA, Perrone-Bizzozero NI. Meta gene set enrichment analyses link MIR137-regulated pathways with schizophrenia risk. Front Genet. 2015;6:147.
Kenny EM, Cormican P, Furlong S, Heron E, Kenny G, Fahey C, et al. Excess of rare novel loss-of-function variants in synaptic genes in schizophrenia and autism spectrum disorders. Mol Psychiatry. 2013;19:872–9.
Funding and disclosure
AR and KKN were supported by the Irish Research Council GOPIG/2013/763 and by the Science Foundation Ireland [11/SIRG/B2183] to KKN, including support for LANG. Funding support for the Genome-Wide Association of Schizophrenia Study was provided by the National Institute of Mental Health (R01 MH67257, R01 MH59588, R01 MH59571, R01 MH59565, R01 MH59587, R01 MH60870, R01 MH59566, R01 MH59586, R01 MH61675, R01 MH60879, R01 MH81800, U01 MH46276, U01 MH46289 U01 MH46318, U01 MH79469, and U01 MH79470) and the genotyping of samples was provided through the Genetic Association Information Network. The datasets used for the analyses described in this manuscript were obtained from the database of Genotypes and Phenotypes (dbGaP) found at http://www.ncbi.nlm.nih.gov/gap through dbGaP accession numbers phs000021/SARC, phs000167/GRU and phs000167/SARC. Samples and associated phenotype data for the Genome-Wide Association of Schizophrenia Study were provided by the Molecular Genetics of Schizophrenia Collaboration (PI: Pablo V. Gejman, Evanston Northwestern Healthcare and Northwestern University, Evanston, IL, USA). The PGC receives core support from NIMH (1U01MH109514-01). Statistical analyses were carried out on the Genetic Cluster Computer (http://www.geneticcluster.org) hosted by SURFsara and financially supported by the Netherlands Scientific Organization (NWO 480-05-003 PI: Posthuma) along with a supplement from the Dutch Brain Foundation and the VU University Amsterdam. Funding for data collection and genotyping was provided by numerous funding organizations internationally. A list is provided in the original PGC manuscript. A list of all members of the Schizophrenia Working Group of the Psychiatric Genomics Consortium 2 can be found in the supplemental information file. The authors declare no competing interests.
Author information
Authors and Affiliations
Consortia
Corresponding authors
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Detailed information regarding members of the Schizophrenia Working Group of the Psychiatric Genomics Consortium 2 can be found in the supplemental information file.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rammos, A., Gonzalez, L.A.N., The Schizophrenia Working Group of the Psychiatric Genomics Consortium 2,. et al. The role of polygenic risk score gene-set analysis in the context of the omnigenic model of schizophrenia. Neuropsychopharmacol. 44, 1562–1569 (2019). https://doi.org/10.1038/s41386-019-0410-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41386-019-0410-z
This article is cited by
-
Cell-type-specific Alzheimer’s disease polygenic risk scores are associated with distinct disease processes in Alzheimer’s disease
Nature Communications (2023)
-
AI-based analysis of social media language predicts addiction treatment dropout at 90 days
Neuropsychopharmacology (2023)
-
The neural signatures of psychoses in Alzheimer’s disease: a neuroimaging genetics approach
European Archives of Psychiatry and Clinical Neuroscience (2023)
-
Recent natural selection conferred protection against schizophrenia by non-antagonistic pleiotropy
Scientific Reports (2023)
-
Predicting mortality among ischemic stroke patients using pathways-derived polygenic risk scores
Scientific Reports (2022)