Abstract
Matrix computation, as a fundamental building block of information processing in science and technology, contributes most of the computational overheads in modern signal processing and artificial intelligence algorithms. Photonic accelerators are designed to accelerate specific categories of computing in the optical domain, especially matrix multiplication, to address the growing demand for computing resources and capacity. Photonic matrix multiplication has much potential to expand the domain of telecommunication, and artificial intelligence benefiting from its superior performance. Recent research in photonic matrix multiplication has flourished and may provide opportunities to develop applications that are unachievable at present by conventional electronic processors. In this review, we first introduce the methods of photonic matrix multiplication, mainly including the plane light conversion method, Mach–Zehnder interferometer method and wavelength division multiplexing method. We also summarize the developmental milestones of photonic matrix multiplication and the related applications. Then, we review their detailed advances in applications to optical signal processing and artificial neural networks in recent years. Finally, we comment on the challenges and perspectives of photonic matrix multiplication and photonic acceleration.
Similar content being viewed by others
Introduction
Over the past few years, there has been an ever-growing demand for artificial intelligence and fifth-generation communications globally, resulting in very large computing power and memory requirements. The slowing down or even failure of Moore’s law makes it increasingly difficult to improve their performance and energy efficiency by relying on advanced semiconductor technology1,2. Moreover, the clock frequency of traditional electrical processing methods is generally limited to several GHz3, which can no longer meet the demands of super-high-speed and low-latency mass data processing. Matrix computation is one of the most widely used and indispensable tools of information processing in science and engineering4,5. Most signal processing, such as the discrete Fourier transform and convolution operation, can be attributed to matrix computations. On the other hand, since the concept of artificial intelligence (AI) was put forward in 1956 for the first time6, artificial neural networks (ANNs) have been rapidly developed and widely used in various fields7. Due to the continuous substantial increase in information capacity, general electronic processors seem to be incapable of executing high-complexity AI tasks in the foreseeable future1. To solve this challenge, chips oriented to AI applications have emerged, such as neural network processing units (NPUs)8. At present, AI chips have been widely used in almost every type of big data processing in areas such as search, news, e-commerce, cloud computing, and inverse design of functional devices9,10,11,12,13. Typically, neural network algorithms represented by deep learning, such as forward neural networks (FNNs), convolutional neural networks (CNNs) and spiking neural networks (SNNs), are characterized by many training parameters, especially in heavy matrix computations14.
Traditionally, matrix computation is completed by an electrical digital signal processor, and its speed and power consumption are greatly limited by the nature of the electronic devices themselves. Therefore, traditional electrical methods are hard to simultaneously achieve high-capacity and low-latency matrix information processing limited by the Moore’s law1,2. However, for some applications, such as ultrafast neural networks15, large bandwidth and low latency are simultaneously required; thus, a new medium for matrix computations and interconnects is urgently needed for the implementation of high-performance and energy-efficient matrix computations. Optical devices can have a superlarge bandwidth and low power consumption16. And light has an ultrahigh frequency up to 100 THz and multiple degrees of freedom in their quantum state17,18, making optical computing one of the most competitive candidates for high-capacity and low-latency matrix information processing in the “More than Moore” era1. For example, a Fourier transform was performed at the speed of light with a lens19. Motivated by its very high prospect, photonic matrix multiplication has been developed rapidly in recent years and has been widely applied in photonic acceleration for optical signal processing20,21,22, AI and optical neural networks (ONNs)15,23,24. A lot of review works on photonic acceleration have been made, these works mainly focused on integrated photonic neuromorphic systems1,15,23,24,25,26,27,28, nanophotonics and machine learning blend29,30, reservoir computing31, programmable nanophotonics21,22,32. As a fundamental and important part of photonic acceleration, photonic matrix multiplication computation for photonic acceleration has not been systematically reviewed. Here, we review the advances of photonic acceleration from the perspective of photonic matrix multiplication. We first discuss the methods and developmental milestones of photonic matrix multiplications and then review the progress in cutting-edge fields of optical signal processing and optical neural networks. Finally, a perspective for photonic matrix multiplications is discussed.
Matrix-vector multiplication
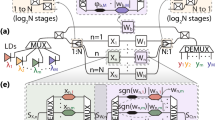
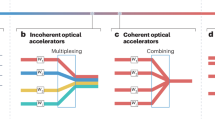
The methods for photonic matrix-vector multiplications (MVMs) mainly fall into three categories: the plane light conversion (PLC) method, Mach–Zehnder interferometer (MZI) method and wavelength division multiplexing (WDM) method. The detailed mechanism of these MVMs can be found in ref. 33, which offers an easy-to-read overview of principle and development of photonic matrix computation. The first kind of optical MVM (PLC-MVM) is implemented by the diffraction of light in free space. Figure 1a shows a typical MVM configuration34,35. First, the incident vector of X distributed along the x direction can be expanded and replicated along the y direction through a cylindrical lens or other optical elements. Then, the spatial diffraction plane is used to adjust each element independently, and its transmission matrix is W. Finally, the x-direction beams are combined and summed in a similar way, and the final output vector of Y along the y direction is the product of the matrix of W and the vector X, that is, Y =WX. The second MVM mainly consists of an MZI network (i.e., MZI-MVM). Figure 1b shows the configuration diagram, which is based mainly on rotation submatrix decomposition and singular value decomposition36. The calibration of the transmission matrix is more difficult since every matrix element is affected by multiple dependent parameters. The third MVM (i.e., WDM-MVM) is an incoherent matrix computation method based on the WDM technology. Figure 1c shows a typical diagram based on microring resonators (MRRs). The input vector of X is loaded on beams with different wavelengths, which pass through the microrings with one-one adjustment of the transmission coefficients of W. Then, the total output power vector is given by Y=WX.
Photonic matrix multiplication has come a long way and developed rapidly in recent years. Figure 2 summarizes the development history and milestones of photonic matrix computation. In the preliminary stage, only some fixed matrix computations were implemented using optical methods such as the Fourier transform19. Thereafter, the initially programmable MVM was demonstrated with spatial optical elements based on single PLC (SPLC)34. For example, a fully parallel, high-speed incoherent optical method was employed to utilize the discrete vector multiplier at a high speed37, while the update of the matrix at high frame rates was restrained with current spatial light modulators (SLMs). Matrix multiplications involving optical array modulators, such as electrooptic modulations, direct driven LED arrays, and acousto-optic Bragg cells, were accomplished with faster frame rates34,38,39. A photorefractive crystal40,41,42 and nonlinear material43 could be optionally applied to implement MVMs. In the SPLC-MVM method, only one dimension is used for the input/output vectors, and the scale (\(\propto N\)) of vectors is still limited. A more powerful PLC-MVM for unitary spatial mode manipulation was proved with multiplane light conversion (MPLC)44,45, in which the input/output vectors are distributed in the whole two-dimensional plane, and the scale is proportional to\({N}^{2}\). Afterwards, the MPLC technique was widely used in various fields, such as for all-optical machine learning46,47,48, the Laguerre-Gaussian or orbital angular momentum (OAM) mode sorter49,50, the photonic Ising machine51,52, time-reversed optical waves53, optical logic operations54, optical encryption and perceptrons55,56, optical hybrid57 and neuromorphic optoelectronic computing58. Although MPLC can achieve ultralarge-scale MVMs, the devices are bulky, and the reprogramming speed for weight encoding is still limited. A mini-sized and universal MVM is more practical, especially in integrated photonic applications. In 2017, Tang et al. first proposed a novel integrated reconfigurable unitary optical mode converter using multimode interference couplers, which shared a similar principle with MPLC59. Then, it was used for all-optical on-chip multi-input-multi-output (MIMO) mode demultiplexing60. In 2020, the integrated MPLC technique was further analyzed by Saygin et al. as a novel matrix decomposition method based on multichannel blocks61 and then was experimentally proven on a silicon photonic chip62.
In 1994, Reck et al. proposed a recursive algorithm that could factorize any \(N\times N\) unitary matrix into a sequence of two-dimensional matrix transformations, which paved the way for future photonic integrated computation based MZIs36. Then, Miller et al. suggested that the MZI network could be self-configured to define functions assisted by transparent detectors63,64,65,66. The MZI mesh was then applied in an add-drop multiplexer for spatial modes66, universal linear optical components65, automatic MIMO64 and universal beam couplers63. In 2016, Clements et al. proposed a brand-new universal matrix framework based on an alternative assemblage of MZIs and phase shifters, which is superior to that proposed by Reck et al. Only half the optical depth of the Reck design is required, and the optical loss is significantly reduced67. Ribeiro et al. experimentally demonstrated a 4 × 4-port universal optical linear circuit chip with the MZI mesh on integration platforms68. Thereafter, the applications of MZI-MVMs were further extended to ONNs3, light descramblers69, modular linear optical circuits70, optical CNNs71, equalizers72, digital-to-analog conversion (DAC)73, Ising machines74,75, mode analysis76 and complex ONNs77.
Generally, the footprint of the MZI reaches over 10,000 μm2 per interferometer unit, which remains a bottleneck to further improve the computing density of the MZI mesh. The WDM-MVM based on microring arrays was proposed by Xu et al., who used compact microrings with a diameter of only a few microns78,79. This approach encodes information on different optical wavelengths rather than spatial modes. Compared to other physical dimensions, the wavelength dimension has the most abundant orthogonal channels in optics, up to hundreds of channels80,81. Silicon MRR arrays for matrix operations were first conceptualized by Xu and Soref in 201178. They were then demonstrated by Yang et al. using a 4 × 4 silicon microring modulator array but with binary values of 0 and 1 only79. In 2014, Tait and his colleagues proposed using MRR arrays as a matrix computation method primitive for photonic neural networks82 and achieved continuous matrix values from -1 to 1 by continuously tuning the MRRs. The WDM-MVM was further used for photonic weight banks83,84,85,86, principal component analysis (PCA)87, independent component analysis (ICA)86, blind source separation (BSS)88, TeraMAC neuromorphic photonic processor18, the optical SNN89, TeraMAC photonic tensor core90, optical CNN91,92,93, and photonic convolutional accelerator for the ONN16,94.
Table 1 summarizes the performance comparison of different photonic matrix multiplication methods. In general, the PLC-MVM method is coherent and can operate in the whole complex field. Its scale is very large, input vector sizes of 357 for SPLC-MVM48 and 490000 (N = 700) for MPLC-MVM58 were reported, easily up to 103 for SPLC-MVM and 106 for MPLC-MVM with SLMs58. However, the device size is quite large, and hence, the integrated counterpart was pursued59,60,61. The MZI-MVM method is also coherent, but its scale is far smaller than that of the PLC-MVM method (N = 64 was reported by Lightmatter95). The main advantage is that it can be integrated into a chip. The WDM-MVM method is more compact. The scale is restricted by the number of wavelengths and can be ~102 with soliton crystal microcombs16, provided all the wavelengths are used for a single MVM. A balanced photodetector summing weighted signals allows for positive and negative weights82. WDM-MVM is incoherent and can be used for real-valued matrices. For these methods, the assigned transmission matrices for SPLC-MVM and WDM-MVM can be directly written in, while some algorithms are needed to load the transmission matrices for the MPLC-MVM and MZI-MVM methods. All these MVM methods have been widely applied in various fields. In the following, we review the detailed applications of MVMs in optical signal processing and photonic AI.
MVMs for optical signal processing
The photonic matrix multiplication network itself can be used as a general linear photonic loop for photonic signal processing32. In recent years, MVM has been developed as a powerful tool for a variety of photonic signal processing methods.
MPLC-MVMs
Benefiting from the large-scale computing capability of spatial planes, MPLC can achieve very powerful matrix functions44. For example, Joel Carpenter et al. realized the classification of 210 Hermite–Gaussian modes or Laguerre-Gaussian modes using only 7 phase planes with a pixel size of \(274\times 274\)49. A schematic diagram of the Laguerre-Gaussian mode sorter is shown in Fig. 3a. First, Gaussian beams from different positions were injected into the device and converted to different orthogonal Hermite–Gaussian modes by MPLC based on the wavefront matching method96. Then, a cylindrical lens pair was used to convert the Hermite–Gaussian mode into the Laguerre-Gaussian mode. The realized super-multimode multiplexer and demultiplexer are of great significance in multimode optical communications. As shown in Fig. 3b, this powerful mode sorter was further used to create time-reversed waves, where all classical linear physical dimensions of light were simultaneously controlled independently53. This device can independently address the amplitude, phase, spatial mode, polarization and spectral/temporal degrees of freedom simultaneously through the programming of the SLM. Ninety spatial/polarization modes controlled over 4.4 THz at a resolution of ~15 GHz were demonstrated, covering a total of ~26,000 spatiospectral modes. A reprogrammable metahologram was further designed for optical encryption, as shown in Fig. 3c55. The encrypted information was divided into two matrices using two phase planes, and the enciphered message emerged only when the two planes matched.
a Laguerre-Gaussian mode sorter49. b Arbitrary vector spatiotemporal field generation53. c Optical encryption55. a Reprinted from ref. 49 with permission from Springer Nature: Nature Communications. b Reprinted from ref. 53 with permission from Springer Nature: Nature Communications. c Reprinted from ref. 55 with permission from Springer Nature: Nature Communications
Some other applications have also been demonstrated. The MPLC technique was a helpful tool for optimal transverse distance estimation, as shown in Fig. 4a97. The measurements were performed in two dimensions far beyond the Rayleigh limit over a large dynamic range. Some theoretical studies were performed. For example, a scalable nonmode selective Hermite–Gaussian mode multiplexer was proposed, as shown in Fig. 4b, where 256 Hermite–Gaussian modes were designed using only seven phase masks98. In Fig. 4c, Li et al. implemented the linear polarization mode and Hermite–Gaussian mode demultiplexing hybrids with similar methods99,100. Each input mode was converted to four fundamental modes with a 90-degree phase difference located at nonoverlapping positions. Local light was uniformly mapped to the fundamental modes with the same phase, which exactly overlapped with output spots from the input modes. The complex amplitudes of the input modes could be retrieved from the interference light intensities. Furthermore, an ultrabroadband polarization-insensitive optical hybrid using MPLC was experimentally verified57. As shown in Fig. 4d, 14 phase masks and a gold mirror were employed to carry out the optical hybrid, and a measurement bandwidth of 390 nm was obtained.
a Transverse distance estimation97. b Nonmode selective Hermite–Gaussian mode multiplexer98. c Mode demultiplexing hybrid100. d Ultrabroadband polarization-insensitive optical hybrid57. a Reprinted with permission from ref. 97 © The Optical Society. b Reproduced from ref. 98 with the permission of Chinese Laser Press. c Reproduced from ref. 100 with the permission of Chinese Laser Press. d Reprinted from ref. 57 with the permission of IEEE Publishing
Integrated MPLC-MVM was also successfully verified. In 2017, Tang et al. first theoretically proved a novel integrated reconfigurable unitary MPLC-MVM using multimode interference couplers59. The schematic diagram is presented in Fig. 5a. The transmission matrix was decomposed into a series of programmable unitary diagonal matrices and fixed unitary diffractive matrices. In theory, an arbitrary unitary transmission matrix can be configured by tuning the unitary diagonal matrices, provided that enough phase planes are assigned. In 2018, the integrated MPLC-MVM was experimentally verified for reconfigurable all-optical on-chip MIMO three-mode demultiplexing60. Figure 5b shows the details of the three-channel MIMO demultiplexing chip. Furthermore, Saygin et al. built a more universal architecture for integrated MPLC-MVM in 202061. In addition, a ten-port unitary optical processor has been experimentally demonstrated62. Figure 5c presents the device operating principle, where the fixed unitary diffractive matrices are implemented using multiport directional couplers. This processer offers a new flexible and robust architecture for large-scale MVMs.
MZI-MVMs
The MZI-MVM, as an integrated photonic matrix computation method, is quite suitable in on-chip optical signal processing32,70. Based on the orthogonal matrix transformation, it is competent to manipulate the spatial orthogonal modes. Figure 6a shows a reconfigurable add-drop multiplexer for spatial modes sampled by the grating array66. It could extract a specified spatial mode from a light beam, leaving the other modes undisturbed. It also allows a new signal to be reloaded on that mode. Similarly, as Fig. 6b shows, an MZI mesh based on the orthogonal matrix transformation was used as a 4 × 4-port universal linear circuit, enabling self-adaptation to implement the desired functions68. The same structure shown in Fig. 6c could further automatically undo strong mixing between modes as a mode descrambler69. The theoretical analysis for the initialization procedure, training and optical multiple-input multiple-output equalizers was discussed in detail in refs. 72,101,102. More generally, the MZI-based orthogonal matrix mesh was theoretically proved to have the ability to analyze and generate multiple modes using self-configuring methods76. The concept and architecture are presented in Fig. 6d, where an example of a square grating coupler array is illuminated by the input light. While these self-configuring methods require many built-in optical power monitors, they bring additional loss and rapidly increase the number of monitors with the extension of the network, making both the electronic layout and iterative algorithm quite complex. In 2020, Zhou et al. proposed and experimentally demonstrated a common self-configuring method without any information from the inner structure103,104. Figure 6e shows an example of the iteration process, where a switching matrix was self-configured from a random state. The training was finished using the numerical gradient algorithm inspired by deep learning3, which is practicable for a general “black box” system. A similar idea was applied for an all-in-one photonic polarization processor chip105,106. Other MZI meshes were also reported for multipurpose silicon photonics signal processors, such as a hexagon mesh107 and a square mesh108.
a Add-drop mode multiplexer66. b 4 × 4-port universal linear circuit68. c Optical mode descrambler69. d Analysis and generation of multimode optical fields76. e Self-configured example103. a Reprinted with permission from ref. 66 © The Optical Society. b Reprinted with permission from ref. 68 © The Optical Society. c Reproduced from ref. 69 with permission of Springer Nature: Light: Science & Applications. (d) Reprinted with permission from ref. 76 © The Optical Society. e Reprinted from ref. 103 with the permission of ACS Publishing
WDM-MVMs
The WDM-MVM can be directly executed without any algorithms, benefiting from the one-to-one mapping relation between wavelengths and matrix elements. This correlation makes the WDM methods practicable for wave shaping combined with frequency–time mapping109,110. As shown in Fig. 7a, b, a 1 × 8 MRR array was fabricated for on-chip programmable pulse shaping. The spectral shape and width could be tuned by changing the resonant wavelengths of the MRRs. The square-shape transfer function is demonstrated and presented in Fig. 7b. Other shapes, such as an isosceles triangle and a sawtooth triangle, were also verified. Furthermore, the MRR array can be used for MVM, provided that a sum operation on multiple wavelengths is performed, called “microring weight banks”, as shown in Fig. 7c83. A balanced photodetector (PD) yielded the sum and difference of weighted signals. The reconfigurability and scalability of the channel count of the MRR weight banks were experimentally demonstrated in ref. 111 with a comprehensive theoretical analysis112. Different methods of controlling large-scale MRRs for matrix computation were proposed and demonstrated in refs. 85,113,114. Afterwards, the microring weight bank was applied for various signal processing methods, such as fiber nonlinearity compensation115 and photonic PCA87. PCA aims to extract the principal components (PCs) solely based on the statistical information of the weighted addition output. Figure 7d presents an experimental example of the obtained two-channel waveforms of both the 1st and 2nd PCs, evidencing the effectiveness of photonic PCA. The weight bank was further used for photonic ICA to identify the underlying sources that form the basis of the observed data86. As shown in Fig. 7e, photonic ICA retrieved the corresponding independent components (ICs) from the received mixture waveforms. By combining the photonic PCA and ICA together, a two-step procedure for a complete photonic BSS pipeline was achieved88. The BSS is a powerful technique for achieving signal decomposition with minimal knowledge on either the source characteristics or the mixing process. Figure 7f gives an example of ICs retrieved from mixed radio-frequency waveforms with the BSS technique88.
a, b On-chip programmable pulse processor employing a cascaded MZI-MRR structure110. c Microring weight banks83. d Photonic principal component analysis87. e Photonic independent component analysis86. f Radio-frequency blind source separation88. a, b Reproduced from ref. 110 with permission of Springer Nature: Nature Photonics. c Reprinted with permission from ref. 83 © The Optical Society. d Reprinted with permission from ref. 87 © The Optical Society. e Reprinted with permission from ref. 86 © The Optical Society. f Reprinted with permission from ref. 88 © The Optical Society.
In comparison, coherent MVMs are usually applied in multimode signal processing. The MPLC method can manage massive modes benefiting from the ability of large-scale matrix computation. The main limits are that it is bulky and difficult to refresh with a fast response. The MZI method is easy to integrate, and the functions of the MZI mesh can be autoconfigured since the phase shifters can work faster. However, the scale of matrix computation is limited, and this method can work only for a few modes. Compared with the MZI method, the WDM-MVM method has a more compact footprint, and it is much easier to configure the transmission matrix and apply WDM-MVM for programmable pulse shaping, photonic PCA, ICA and BSS.
MVMs for optical neural networks
AI technology has been widely used in various electronics industries, such as for deep-learning-based speech recognition and image processing. MVM, as the basic building block of ANNs, occupies most of the computing tasks, such as over 80% for GoogleNet and OverFeat models116. Improving the MVM performance is one of the most effective means for ANN acceleration. Compared with electrical computing, optical computing is poor at data storage and flow control, and the low efficiency of optical nonlinearities limits the applications in nonlinear computation117, such as activation functions. While it has significant advantages on massively parallel computing through multiplexing strategies of wavelength, mode and polarization17,90, extremely high data modulation speeds up to 100 GHz118,119. Hence, photonic networks are quite good at MVM. The combination of optical computing and AI is expected to realize intelligent photonic processors and photonic accelerators120. In recent years, AI technology has also seen rapid developments in the field of optics.
MPLC-MVMs
MPLC, as a supersized MVM method, is an inborn alternative to the ONN. In 2018, Lin et al. presented an all-optical diffractive deep neural network (D2NN) architecture to perform machine learning46. The schematic diagram is shown in Fig. 8a. Five phase-only transmission masks were used to classify images of handwritten digits and fashion products at the speed of light. Then, a modified D2NN based on class-specific differential detection was designed to improve the inference accuracy47. The information processing capacity of MPLC was recently discussed in detail by Kulce et al.121, proving that the dimensionality of the all-optical solution space is linearly proportional to the number of phase planes. While it may be difficult to train the D2NN due to the existence of vanishing gradients, it has been suggested to address this issue by directly connecting the input and output using a learnable light shortcut, which offers a direct path for gradient backpropagation in training122. The MPLC-D2NN can be applied not only in image identification but also in optical logic operations54, OAM multiplexing and demultiplexing50, optical linear perceptrons56 and Ising machines52. As shown in Fig. 8b, the optical logic functions were performed by a two-layer D2NN, and different logic operations were output from different ports after the training54. The incident wave was physically encoded at the input layer, and then the compound metasurfaces (hidden layer) scattered the encoded light into one of two small designated areas at the output layer, which provided information on the output logic states. On this foundation, multiple logic gates can be further cascaded to enable more complex or customer-defined functionalities. This universal design strategy holds potential in several applications, such as cryptographically secured wireless communication, real-time object recognition in surveillance systems, and intelligent wave shaping inside biological tissues. Figure 8c presents the coupling and separation of OAM modes with the D2NN. Here, four plane masks with pixels of 256×256 were designed to couple and separate four OAM modes. The optical machine learning decryptor in Fig. 8d was realized with single-layer holographic perceptrons, which were trained to complete optical inference missions56. This decryptor could perform optical inference for single or whole classes of keys through symmetric and asymmetric decryption. The decryptors could be nanoprinted on complementary metal-oxide–semiconductor (CMOS) chips by galvo-dithered two-photon nanolithography (GD-TPN) with axial nanostepping of 10 nm. The high resolution achieved by GD-TPN allowed achieving a small feature size for the holographic perceptrons at near-infrared telecommunication wavelengths and a neuron density of >500 million neurons per square centimeter. MPLC was also applied in a spatial-photonic Ising machine. The principle of a photonic Ising machine with spatial light modulation is depicted in Fig. 8e51,123. The spins were encoded into binary optical phases of 0 and π at separated spatial points by an SLM. Intensity modulation was used to set the spin interaction via another SLM. Recurrent feedback from the far-field camera allowed evolution of the phase configuration toward the Ising ground state. It developed a novel hardware with an optics-enabled parallel architecture for large-scale optimizations. A photonic scheme for combinatorial optimization analogous to adiabatic quantum algorithms and classical annealing methods was further studied52. More recently, Ruan et al. experimentally evaluated the phase diagram of a high-dimensional spin-glass equilibrium system with 100 fully connected spins under gauge transformation124 and synchronously proposed implementing an antiferromagnetic model through optoelectronic correlation computation with 40000 spins for the number-partitioning problem125. The nonlinear activation functions for D2NN were also proved using laser-cooled atoms with electromagnetically induced transparency126. To seek a more general and reconfigurable MPLC-based ONN, an optoelectronic fused computing framework based on optical diffraction was proposed, which supports several kinds of neural networks and maintains a high model complexity with millions of neurons58. The principle diagram of the basic diffractive processing unit (DPU) is presented in Fig. 9a, b. A digital micromirror device (DMD) and an SLM were assembled to implement the input nodes, and a CMOS sensor was used to implement the optoelectronic neurons. It consists of large-scale diffractive neurons and weighted optical interconnections, enabling the processing of large-scale visual signals, such as images and videos. Three types of ONNs were configured, including the D2NN in Fig. 9c, the diffractive network in network (D-NIN-1) in Fig. 9d, and the diffractive recurrent neural network (D-RNN) in Fig. 9e.
a Classification of images of handwritten digits and fashion products46. b Optical logic operations54. c OAM multiplexing and demultiplexing50. d Optical linear perceptrons56. e Photonic Ising machine51,123. a Reprinted by permission from AAAS46. b Reproduced from ref. 54 with permission of Springer Nature: Light: Science & Applications. c Reprinted from ref. 50 with the permission of IEEE Publishing. d Reproduced from ref. 56 with permission of Springer Nature: Light: Science & Applications. e Reproduced from ref. 123. with permission of De Gruyter Publishing
a DPU. b Programmable optoelectronic devices to implement the DPU. c–e Three different types of neural network architectures were constructed, including the D2NN, D-NIN-1, and D-RNN. a–e Reproduced from ref. 58 with permission of Springer Nature: Nature Photonics
MZI-MVMs
Different from MPLC-MVM, the main advantage of MZI-MVM is the potential small size, allowing miniaturized ONN chips. In 2017, Shen et al. proposed a new architecture for a fully optical feedforward neural network, as shown in Fig. 10a3. The device, containing 56 programmable MZIs, demonstrated its utility for vowel recognition. It improved the computational speed and power efficiency over advanced electronics for conventional deep learning tasks. Thereafter, an optical convolutional neural network was further proposed. As shown in Fig. 10b, the optical delay lines were implemented with microrings, and the MVM was implemented efficiently in photonic circuits by an MZI mesh71. However, the training of these networks was quite difficult and should be followed. Hughes et al. introduced a highly efficient method for in situ training of an ONN. Figure 10c presents a schematic illustration of the proposed method, which uses adjoint variable methods to derive the photonic analog of the backpropagation algorithm127. The genetic algorithm was also demonstrated as an efficient method to on-chip train the ONNs128. A similar mesh could be expanded to implement a complex-valued neural network77. As shown in Fig. 11a, the complex-valued ONN could encode information in both phase and magnitude with MZIs (marked in red). The reference light used for coherent detection was introduced by the MZI in green. The complex-valued weight matrix was implemented with the MZIs in blue. Then, on-chip coherent detection was implemented by the remaining black MZIs. The input preparation, weight multiplication and coherent detection were all integrated onto a single chip, which offered significantly enhanced computational speed and energy efficiency.
a Optical feedforward neural network3. b Optical convolutional neural network71. c In situ training of an ONN127. a Reproduced from ref. 3 with permission of Springer Nature: Nature Photonics. b Reproduced from ref. 71 with the permission of the authors. c Reprinted with permission from ref. 127 © The Optical Society
a Complex-valued ONN with MZI mesh77. b, c Photonic recurrent Ising machines with MZI mesh74. b The principle of Ising machines and c the energy evolution as a function of time. a Reprinted from ref. 77 with permission from Springer Nature: Nature Communications. b, c Reprinted with permission from ref. 74 © The Optical Society
In addition to neural networks, efforts have also been made to unleash the potential of these photonic architectures by developing algorithms that optimally exploit photonic fundamental advantages. In 2020, Roques-Carmes and Shen et al proposed the photonic recurrent Ising sampler (PRIS)75, a heuristic method tailored for parallel architectures allowing fast and efficient sampling from distributions of arbitrary Ising problems. They later experimentally demonstrated the PRIS by combining electronics and silicon-on-insulator photonics74. Figure 11b presents the algorithm iteration of the PRIS. The spin state vector was encoded in the amplitudes of coherent optical signals at the input. The transmission matrix of the MZI mesh was dependent on the problem-specific Ising coupling matrix. The output of the matrix multiplication is noisy with Gaussian perturbation. After several algorithm steps, the energy shown in Fig. 11c could approach the ground state, and then the results of optimization for a specific Ising problem were obtained.
WDM-MVMs
In 2014, Tait and his colleagues proposed, for the first time, using MRR arrays as a matrix computation method primitive for photonic neural networks82. This work, for the first time, introduced a scalable neural network architecture called “broadcast-and-weight” based on the WDM concept. In this architecture, as shown in Fig. 12a, neural network weights can be continuously tuned to achieve both positive and negative weights analogous to neural weights. In the same work82, Tait et al. also first introduced a network design allowing scalable and cascadable ONNs by employing wavelength reuse, followed by an experimental demonstration in 201784, concurrently with other silicon photonic neuromorphic architectures3. This network architecture can be applied to construct both feedforward and recurrent neural networks. Microring weighting banks were also employed for optical CNNs91,92,93. In CNNs, as shown in Fig. 12b, the input images are divided into small patches, and these patches are converted into small matrices for MVM operations. In 2019, an all-optical spiking neural network based on phase-change materials (PCMs) was experimentally demonstrated89. As shown in Fig. 12c, the input vectors were loaded on beams with different wavelengths and weighted by PCMs. Moreover, the nonlinear activation function was implemented in optics by changing the resonant wavelengths of the microring when the summed power altered the state of PCMs. Figure 12d shows a photonic tensor core for neural networks using PCMs as the reconfiguration elements129. The input matrix was modulated by high-speed modulators, and the kernel matrix was loaded using photonic memory based on PCMs. The weighted inputs were then incoherently summed using a photodetector.
a Optical broadcast-and-weight network showing parallels with the neural network mode82,84. b Optical convolutional neural network92. c All-optical spiking neurosynaptic networks89. d Photonic dot product engine for machine learning129. a Reprinted from ref. 82 with the permission of IEEE Publishing. b Reprinted from ref. 92 with the permission of IEEE Publishing. c Reprinted from ref. 89 with permission from Springer Nature: Nature. d Reproduced from ref. 129 with the permission of AIP Publishing
Recently, a convolutional photonic processor with extremely high computing throughputs was demonstrated by exploring different dimensions of light. Feldmann et al. demonstrated a highly parallel convolutional processer using an integrated photonic tensor core, achieving 1012 multiply-accumulate operations per second90. A conceptual illustration of the photonic architecture is shown in Fig. 13a. Highly parallel MVMs were performed by using multiple groups of wavelengths generated from a soliton-based optical frequency comb. PCMs were applied as nonvolatile actuators, and thus, convolutional processing can be performed with extremely low power. Another photonic convolutional accelerator realized highly parallel computing by utilizing wavelength-and-time interleaving, as shown in Fig. 13b, which achieved up to 10 trillion operations per second16. The input data vector was encoded as the intensity of light with an electro-optical Mach–Zehnder modulator (EOM), and then the wavelength-dependent delay achieved by a single-mode fiber (SMF) was used to reshape the signals at different wavelengths. The convolutional operation was performed at the speed of light by summing the powers at presupposed wavelengths after spectral shaping. These works suggest that photonics is coming of age and in some cases can begin to outperform electronic computation.
Regarding neural networks, all three MVM methods can be used in the linear part of neural networks to achieve photonic acceleration. In contrast, MPLC-based ONNs have the most powerful computing ability and can solve classification problems with all-optical methods, but the refresh rate of spatial planes is limited. MZI-based ONNs are reconfigurable for different situations, but their scale is limited, and electronics-aided learning is needed for complex tasks. To date, WDM-based ONNs have a larger scale than MZI-based ONNs, while they are incoherent computations, where differential detection is often carried out in tandem. Table 2 summarizes the performance comparison of state-of-the-art photonic AI accelerators with electronic hardware. In general, photonic computing has obvious advantages in terms of signal rate, latency, power consumption and computing density, and its accuracy is generally lower than that of electrical computing.
Discussion
Scalability and cascadability of ONNs
There exists a huge gap between the number of weights of ANN in electrical and optical MVMs, for example, the weight parameters of ResNet-50, a popular and widely used deep learning network architecture presented by Microsoft in 2016, have already reached 25 million130. To alleviate the issue, one direct and effective solution is to manufacture larger-scale photonic integrated circuit (PIC) chips, and indeed, Lightmatter Inc. has released the world-record 64×64 sized MZI mesh integrated chip ‘Mars’ in 2020, which is capable of performing 4096 MAC operations each time when a new set of input vectors is fed in, and the computing capacity is estimated to be 8 TOPS95. Similar to integrated circuits, the PIC chips provide the potential to achieve larger scale and higher integration density as the manufacture technologies improve. Furthermore, optical devices promise massive parallelism by employing WDM and mode division multiplexing (MDM)17,90, these parallel operations can be performed in a single physical optical processing core90.
The scale-out issue can also be solved by optimizing and improving optical components. For example, the number of neurons can be further expanded utilizing spectrum reuse strategies for the WDM scheme82, and the topology structures of neuron cluster, small-world neural network, and interconnected SNN PICs were proposed to build larger-scale on-chip photonic neurons28. As the scale of MRR array becomes larger, the controlling technique would be paramount, integrated photoconductive heaters enable control of large-scale silicon photonic MRR array without requiring additional components, complex tuning algorithms, or additional electrical I/Os131. The electro-optical modulators using lithium niobate and barium titanate integrated with silicon photonics offer high-speed phase modulation and low operating voltage, making these devices very attractive for PICs designed for photonic computing132. The maturity of state-of-the-art silicon nitride platform has enabled low-loss waveguides (<1 dB/m), thus reducing energy consumption and cost compared with current digital electronics, and provided opportunities for the practical application of photonic accelerators to SOI and III–V PICs especially when computation bandwidth and modulation rates continue to increase rapidly133. Challenges arise in scaling to larger matrices, since phase shifters in MZI mesh scheme typically consume 10 mW to 20 mW per unit for thermal tuning134, and thermal power consumption accumulation for thousands of phase shifter units will deteriorate the competitiveness of the photonic accelerator. Nano-optical-electro mechanical system (NOEMS) technology can be applied to replace traditional thermal phase shifters to reduce the power consuming of maintaining the status of MZIs135. Compared to thermal phase shifters, the static power dissipation of NOEMS components is nearly zero because mechanical displacements only require a small amount of energy to move the waveguide back and forth.
To form a scalable neural network, optical neurons should be able to excite with a certain strength to evoke at least an equivalent response in a downstream neuron82. To construct a cascadable neuron, the first step is to use an active amplifier, which provides energy gain in the optical or electrical domain136. The second step is to improve the efficiency of optoelectronic devices, which can be achieved by enhancing the interaction between the active materials and propagating waveguide mode (i.e., light-matter interaction) with nanoscale devices and novel materials137,138,139,140. And hybrid integration technology is significant for integrating the low-loss passive silicon or silicon nitride waveguides with the active amplifiers and lasers141,142,143. These promising technologies pave the way for cascadable photonic neurons.
Activation functions
MVMs and activation functions are two basic elements of perceptrons94. Photonic MVMs show significant advantages on signal rate, latency, computing density and power consumption compared to electrical neurons, while photonic activation functions are still not mature. The implementation of photonic neurons relies on the nonlinear response of optical devices. Based on the physical representation of signals inside a neuron, the techniques are divided into two primary categories: optical-electrical-optical (OEO) and all-optical activation functions. OEO neurons convert optical power into an electrical current and then back into the signal pathway. Their nonlinearities manifest themselves in the electrical domain as well as during the EO conversion step, in which lasers144,145,146 or saturation modulators147,148 are employed. Using foundry-compatible silicon-on-insulator (SOI) technology, OEO neurons were demonstrated by Tait et al. using a high-speed silicon MRR modulator147 and by Williamson et al. with a Mach–Zehnder-type modulator149. All-optical neurons depend on semiconductor carriers, reverse saturated absorption, or optical susceptibility, which can be found in a variety of materials150. All-optical neuron implementations are thought to be faster than the OEO techniques. All-optical neurons have been proven using optical nonlinearities, such as the carrier effect in MRRs151,152,153 and the alteration of a material state89,154. Generally, for different AI applications, activation functions need to be chosen dependent on particular tasks. Due to the weak optical nonlinearity, the resonant devices were used to reduce the threshold and simultaneously enhance the phase sensitivity89,152. Huang et al. proposed using multiple coupled cavity devices to optimize different activation functions for different machine-learning tasks152, followed by an experimental demonstration153. And the microring resonators with PCMs were also demonstrated as effective all-optical activation functions89. The active optical devices are also promising candidates for activation functions144,155,156,157. A reconfigurable photonic activation function was also demonstrated using injection-locked Fabry–Perot semiconductor lasers155. The neuronlike excitable behavior in a micropillar laser with saturable absorber was experimentally demonstrated by introducing optical perturbations144. And the vertical-cavity surface-emitting laser with an embedded saturable absorber was employed as a spiking neuron156,157. The semiconductor optical amplifiers were also demonstrated for all-optical activation functions158,159,160,161.
Optoelectronic-hybrid AI
The activation function can be realized by using either electronic or photonic methods. The optical activation function is still in the preliminary research stage, and there is no mature scheme since the efficiency of optical nonlinearity is rather low. The realization of an all-optical activation function with a low loss and a high nonlinear effect remains a key issue in the entire optical network. On the other hand, all-optical cascaded ONNs are still difficult to achieve due to the accumulative loss of optical networks. In fact, only ANNs with quite simple structures or without activation functions were all-optical, such as the SNNs with PCMs89, reservoir computing using optical amplifiers or passive silicon circuits31,162,163, and D2NN with passive phase masks46,47,54. On the contrary, most previous works of deep ANNs were implemented based on optoelectronic-hybrid hardware3,16,18,58,90. Before the all-optical ANNs are mature, especially in optical nonlinear effect and optical cascade, optoelectronic-hybrid AI is a more practical and more competitive candidate for deep ANNs. Therefore, the development of a highly efficient and dedicated optoelectronic-hybrid AI hardware chip system is one of the core research routes of photonic AI.
Photonic matrix multiplication has revealed great potential for optical signal processing and AI acceleration. It can greatly reduce the power consumption and signal delay. In the future, the photonic matrix core would be more comprehensive and cover richer functions. Figure 14 shows a possible route for the optoelectronic-hybrid AI computing chip framework. It mainly contains three layers: the bottom hardware layer, the algorithm layer and the top application layer.
Electronic computing has become quite mature, and it has outstanding advantages in terms of data storage and flow control, which are basically unknown for photonic computing. The computing capacity and speed of photons are superior to those of electronic computing, which can be improved by several orders of magnitude23,164. By combining the advantages of electronic and photonic systems, the performance in terms of the power consumption, computing capacity, computing speed, etc., can be improved by orders of magnitude compared with that of traditional electronic methods3,16,58. The hardware layer is mainly regarded as the photonic AI hardware system built on photoelectric devices. The electronic part of the hardware layer completes the data storage, data write/read, flow control and slight computations. The optical part executes the matrix computation operators, which take up most of the computing tasks58.
The algorithm layer is used to develop universal algorithm frameworks for the photonic AI hardware system, such as linear regression and gradient descent165, or to develop computing models, such as the feedforward neural network and convolutional neural network7. These algorithms can be efficiently executed in the physical layer. Different algorithms can be combined with photoelectric AI hardware depending on the type of problem. For example, the linear regression algorithm is often used in prediction, and logistic regression is often used to solve the problem of binary classification165. Neural network algorithms are the most widely used machine-learning methods and can significantly improve deep learning based on text, images, and voice7. In addition, based on the activation function, various logical computing functions can be developed as the basic unit of the optoelectronic-hybrid digital computer166. The algorithm framework can be learned from the mature AI algorithms of electronic computing, but it should be adjusted appropriately considering the hardware differences.
The application layer is a user-oriented interface based on the entire AI hardware system and algorithm frameworks. Users can develop various applications, such as channel equalization69,103, Google PageRank104, image recognition16,90, and voice recognition3. For example, the linear part of the optical computing core can be directly used in image sharpening, smoothing, etc., as well as in all-optical signal processing (such as channel equalization)167. Neural network algorithms can be employed for image recognition and voice recognition3,16,90. In addition, multiple algorithms can be combined to jointly address optimization and decision issues, such as NP-hard problems and high-speed tracking problems51,74,168. An optical computing system based on digital logic can also be built with all-optical or optoelectronic-hybrid logic computing functions166,169.
In summary, photonic matrix multiplication has been applied in many areas, such as optical signal processing in optical communications and AI accelerators. Numerous promising applications established based on matrix multiplication computation provide a complementary opportunity to expand the domain of photonic accelerators. We have reviewed the recent progress in photonic matrix multiplication with various methods and applications. A perspective for photonic matrix multiplication was further discussed, which might be extended to an easy-to-operate minicomputer for different photonic accelerator applications.
References
Kitayama, K.-I. et al. Novel frontier of photonics for data processing—Photonic accelerator. APL Photonics 4, 090901 (2019).
Waldrop, M. M. The chips are down for Moore’s law. Nature 530, 144–147 (2016).
Shen, Y. C. et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics 11, 441–446 (2017).
Lee, D. D. & Seung, H. S. Learning the parts of objects by non-negative matrix factorization. Nature 401, 788–791 (1999).
Richardson, M. & Domingos, P. The intelligent surfer: probabilistic combination of link and content information in pagerank. In Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic. 1441–1448 (Vancouver British, Columbia, Canada: MIT Press, 2001).
Shannon, C. E. & McCarthy, J. Automata studies. (Princeton, NJ: Princeton University Press, 1956).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Dominey, P. F. & Ramus, F. Neural network processing of natural language: I. Sensitivity to serial, temporal and abstract structure of language in the infant. Lang. Cogn. Process. 15, 87–127 (2000).
Zhen, Z. et al. Realizing transmitted metasurface cloak by a tandem neural network. Photonics Res. 9, B229–B235 (2021).
Qian, C. & Chen, H. S. A perspective on the next generation of invisibility cloaks—Intelligent cloaks. Appl. Phys. Lett. 118, 180501 (2021).
Qian, C. et al. Deep-learning-enabled self-adaptive microwave cloak without human intervention. Nat. Photonics 14, 383–390 (2020).
Chen, X. D. et al. A review of deep learning approaches for inverse scattering problems (invited review). Prog. Electromagnetics Res. 167, 67–81 (2020).
Ma, W. et al. Deep learning for the design of photonic structures. Nat. Photonics 15, 77–90 (2021).
Sarle, W. S. Neural networks and statistical models. In Proceedings of The 19th Annual SAS Users Group International Conference. 1538–1550 (Cary, NC: SAS Institute, 1994).
Shastri, B. J. et al. Photonics for artificial intelligence and neuromorphic computing. Nat. Photonics 15, 102–114 (2021).
Xu, X. Y. et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 589, 44–51 (2021).
Wang, J. et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 6, 488–496 (2012).
Nahmias, M. A. et al. A TeraMAC neuromorphic photonic processor. In Proceedings of 2018 IEEE Photonics Conference (IPC). (Reston, VA, USA: IEEE, 2018).
Von Bieren, K. Lens design for optical Fourier transform systems. Appl. Opt. 10, 2739–2742 (1971).
Pérez, D. et al. Principles, fundamentals, and applications of programmable integrated photonics. Adv. Opt. Photonics 12, 709–786 (2020).
Bogaerts, W. et al. Programmable photonic circuits. Nature 586, 207–216 (2020).
Pérez, D., Gasulla, I. & Capmany, J. Programmable multifunctional integrated nanophotonics. Nanophotonics 7, 1351–1371 (2018).
Zhang, Q. M. et al. Artificial neural networks enabled by nanophotonics. Light Sci. Appl. 8, 1–14 (2019).
de Lima, T. F. et al. Machine learning with neuromorphic photonics. J. Lightwave Technol. 37, 1515–1534 (2019).
Wetzstein, G. et al. Inference in artificial intelligence with deep optics and photonics. Nature 588, 39–47 (2020).
Stark, P. et al. Opportunities for integrated photonic neural networks. Nanophotonics 9, 4221–4232 (2020).
de Lima, T. F. et al. Primer on silicon neuromorphic photonic processors: architecture and compiler. Nanophotonics 9, 4055–4073 (2020).
de Lima, T. F. et al. Progress in neuromorphic photonics. Nanophotonics 6, 577–599 (2017).
Yao, K., Unni, R. & Zheng, Y. B. Intelligent nanophotonics: merging photonics and artificial intelligence at the nanoscale. Nanophotonics 8, 339–366 (2019).
Jiang, J. Q., Chen, M. K. & Fan, J. A. Deep neural networks for the evaluation and design of photonic devices. Nat. Rev. Mater. 6, 679–700 (2021).
Van der Sande, G., Brunner, D. & Soriano, M. C. Advances in photonic reservoir computing. Nanophotonics 6, 561–576 (2017).
Harris, N. C. et al. Linear programmable nanophotonic processors. Optica 5, 1623–1631 (2018).
Cheng, J. W., Zhou, H. L. & Dong, J. J. Photonic matrix computing: from fundamentals to applications. Nanomaterials 11, 1683 (2021).
Athale, R. A. & Collins, W. C. Optical matrix-matrix multiplier based on outer product decomposition. Appl. Opt. 21, 2089–2090 (1982).
Zhu, W. W. et al. Design and experimental verification for optical module of optical vector-matrix multiplier. Appl. Opt. 52, 4412–4418 (2013).
Reck, M. et al. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 73, 58–61 (1994).
Habiby, S. F. & Collins, S. A. Implementation of a fast digital optical matrix–vector multiplier using a holographic look-up table and residue arithmetic. Appl. Opt. 26, 4639–4652 (1987).
Bocker, R. P., Clayton, S. R. & Bromley, K. Electrooptical matrix multiplication using the twos complement arithmetic for improved accuracy: erratum. Appl. Opt. 22, 3149 (1983).
Cartwright, S. New optical matrix–vector multiplier. Appl. Opt. 23, 1683–1684 (1984).
Hong, J. & Yeh, P. Photorefractive parallel matrix–matrix multiplier. Opt. Lett. 16, 1343–1345 (1991).
Beijersbergen, M. W. et al. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 96, 123–132 (1993).
Liu, B. et al. Matrix–vector multiplication in a photorefractive crystal. Opt. Commun. 146, 34–38 (1998).
Mukhopadhay, S. et al. Implementation of all-optical digital matrix multiplication scheme with nonlinear material. Optical Eng. 40, 1998–2002 (2001).
Morizur, J.-F. et al. Programmable unitary spatial mode manipulation. J. Optical Soc. Am. A 27, 2524–2531 (2010).
Labroille, G. et al. Efficient and mode selective spatial mode multiplexer based on multi-plane light conversion. Opt. Express 22, 15599–15607 (2014).
Lin, X. et al. All-optical machine learning using diffractive deep neural networks. Science 361, 1004–1008 (2018).
Li, J. X. et al. Class-specific differential detection in diffractive optical neural networks improves inference accuracy. Adv. Photonics 1, 046001 (2019).
Bernstein, L. et al. Freely scalable and reconfigurable optical hardware for deep learning. Sci. Rep. 11, 3144 (2021).
Fontaine, N. K. et al. Laguerre-Gaussian mode sorter. Nat. Commun. 10, 1865 (2019).
Wang, P. P. et al. Diffractive deep neural network for optical orbital angular momentum multiplexing and demultiplexing. IEEE J. Sel. Top. Quantum Electron. 28, 7500111 (2022).
Pierangeli, D., Marcucci, G. & Conti, C. Large-scale photonic ising machine by spatial light modulation. Phys. Rev. Lett. 122, 213902 (2019).
Pierangeli, D., Marcucci, G. & Conti, C. Adiabatic evolution on a spatial-photonic Ising machine. Optica 7, 1535–1543 (2020).
Mounaix, M. et al. Time reversed optical waves by arbitrary vector spatiotemporal field generation. Nat. Commun. 11, 5813 (2020).
Qian, C. et al. Performing optical logic operations by a diffractive neural network. Light Sci. Appl. 9, 59 (2020).
Qu, G. Y. et al. Reprogrammable meta-hologram for optical encryption. Nat. Commun. 11, 5484 (2020).
Goi, E. et al. Nanoprinted high-neuron-density optical linear perceptrons performing near-infrared inference on a CMOS chip. Light Sci. Appl. 10, 40 (2021).
Zhang, Y. H. et al. An ultra-broadband polarization-insensitive optical hybrid using multiplane light conversion. J. Lightwave Technol. 38, 6286–6291 (2020).
Zhou, T. K. et al. Large-scale neuromorphic optoelectronic computing with a reconfigurable diffractive processing unit. Nat. Photonics 15, 367–373 (2021).
Tang, R., Tanemura, T. & Nakano, Y. Integrated reconfigurable unitary optical mode converter using MMI couplers. IEEE Photonics Technol. Lett. 29, 971–974 (2017).
Tang, R. et al. Reconfigurable all-optical on-chip MIMO three-mode demultiplexing based on multi-plane light conversion. Opt. Lett. 43, 1798–1801 (2018).
Saygin, M. Y. et al. Robust architecture for programmable universal unitaries. Phys. Rev. Lett. 124, 010501 (2020).
Tang, R. et al. Ten-port unitary optical processor on a silicon photonic chip. ACS Photonics 8, 2074–2080 (2021).
Miller, D. A. B. Self-aligning universal beam coupler. Opt. Express 21, 6360–6370 (2013).
Miller, D. A. B. Establishing optimal wave communication channels automatically. J. Lightwave Technol. 31, 3987–3994 (2013).
Miller, D. A. B. Self-configuring universal linear optical component. Photonics Res. 1, 1–15 (2013).
Miller, D. A. B. Reconfigurable add-drop multiplexer for spatial modes. Opt. Express 21, 20220–20229 (2013).
Clements, W. R. et al. Optimal design for universal multiport interferometers. Optica 3, 1460–1465 (2016).
Ribeiro, A. et al. Demonstration of a 4 × 4-port universal linear circuit. Optica 3, 1348–1357 (2016).
Annoni, A. et al. Unscrambling light—automatically undoing strong mixing between modes. Light Sci. Appl. 6, e17110 (2017).
Mennea, P. L. et al. Modular linear optical circuits. Optica 5, 1087–1090 (2018).
Bagherian, H. et al. On-chip optical convolutional neural networks. Preprint at https://arxiv.org/abs/1808.03303 (2018).
Choutagunta, K. et al. Adapting Mach–Zehnder mesh equalizers in direct-detection mode-division-multiplexed links. J. Lightwave Technol. 38, 723–735 (2020).
Cong, G. W. et al. Arbitrary reconfiguration of universal silicon photonic circuits by bacteria foraging algorithm to achieve reconfigurable photonic digital-to-analog conversion. Opt. Express 27, 24914–24922 (2019).
Prabhu, M. et al. Accelerating recurrent Ising machines in photonic integrated circuits. Optica 7, 551–558 (2020).
Roques-Carmes, C. et al. Heuristic recurrent algorithms for photonic Ising machines. Nat. Commun. 11, 249 (2020).
Miller, D. A. B. Analyzing and generating multimode optical fields using self -configuring networks. Optica 7, 794–801 (2020).
Zhang, H. et al. An optical neural chip for implementing complex-valued neural network. Nat. Commun. 12, 457 (2021).
Xu, Q. F. & Soref, R. Reconfigurable optical directed-logic circuits using microresonator-based optical switches. Opt. Express 19, 5244–5259 (2011).
Yang, L. et al. On-chip CMOS-compatible optical signal processor. Opt. Express 20, 13560–13565 (2012).
Karpov, M. et al. Dynamics of soliton crystals in optical microresonators. Nat. Phys. 15, 1071–1077 (2019).
Obrzud, E. et al. A microphotonic astrocomb. Nat. Photonics 13, 31–35 (2019).
Tait, A. N. et al. Broadcast and weight: an integrated network for scalable photonic spike processing. J. Lightwave Technol. 32, 4029–4041 (2014).
Tait, A. N. et al. Multi-channel control for microring weight banks. Opt. Express 24, 8895–8906 (2016).
Tait, A. N. et al. Neuromorphic photonic networks using silicon photonic weight banks. Sci. Rep. 7, 7430 (2017).
Huang, C. R. et al. Demonstration of scalable microring weight bank control for large-scale photonic integrated circuits. APL Photonics 5, 040803 (2020).
Ma, P. Y. et al. Photonic independent component analysis using an on-chip microring weight bank. Opt. Express 28, 1827–1844 (2020).
Ma, P. Y. et al. Photonic principal component analysis using an on-chip microring weight bank. Opt. Express 27, 18329–18342 (2019).
Ma, P. Y. et al. Blind source separation with integrated photonics and reduced dimensional statistics. Opt. Lett. 45, 6494–6497 (2020).
Feldmann, J. et al. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 569, 208–214 (2019).
Feldmann, J. et al. Parallel convolutional processing using an integrated photonic tensor core. Nature 589, 52–58 (2021).
Xu, S. F., Wang, J. & Zou, W. W. Optical convolutional neural network with WDM-based optical patching and microring weighting banks. IEEE Photonics Technol. Lett. 33, 89–92 (2021).
Bangari, V. et al. Digital electronics and analog photonics for convolutional neural networks (DEAP-CNNs). IEEE J. Sel. Top. Quantum Electron. 26, 7701213 (2020).
Xu, S. F., Wang, J. & Zou, W. W. Optical patching scheme for optical convolutional neural networks based on wavelength-division multiplexing and optical delay lines. Opt. Lett. 45, 3689–3692 (2020).
Xu, X. Y. et al. Photonic perceptron based on a kerr microcomb for high-speed, scalable, optical neural networks. Laser Photonics Rev. 14, 2000070 (2020).
Ramey, C. Silicon photonics for artificial intelligence acceleration: Hotchips 32. In Proceedings of 2020 IEEE Hot Chips 32 Symposium (HCS) (Palo Alto, CA, USA: IEEE, 2020).
Sakamaki, Y. et al. New optical waveguide design based on wavefront matching method. J. Lightwave Technol. 25, 3511–3518 (2007).
Boucher, P. et al. Spatial optical mode demultiplexing as a practical tool for optimal transverse distance estimation. Optica 7, 1621–1626 (2020).
Wen, H. et al. Scalable non-mode selective Hermite-Gaussian mode multiplexer based on multi-plane light conversion. Photonics Res. 9, 88–97 (2021).
Wen, H. et al. Scalable Hermite-Gaussian mode-demultiplexing hybrids. Opt. Lett. 45, 2219–2222 (2020).
Wen, H. et al. Mode demultiplexing hybrids for mode-division multiplexing coherent receivers. Photonics Res. 7, 917–925 (2019).
Pai, S. et al. Matrix optimization on universal unitary photonic devices. Phys. Rev. Appl. 11, 064044 (2019).
Zhang, T. et al. Efficient training and design of photonic neural network through neuroevolution. Opt. Express 27, 37150–37163 (2019).
Zhou, H. L. et al. Self-configuring and reconfigurable silicon photonic signal processor. ACS Photonics 7, 792–799 (2020).
Zhou, H. L. et al. Chip-scale optical matrix computation for PageRank algorithm. IEEE J. Sel. Top. Quantum Electron. 26, 8300910 (2020).
Zhou, H. L. et al. All-in-one silicon photonic polarization processor. Nanophotonics 8, 2257–2267 (2019).
Zhou, H. L. et al. Multipurpose photonic polarization processor chip. In Proceedings of 2019 Asia Communications and Photonics Conference (Chengdu, China: IEEE, 2019).
Pérez, D. et al. Multipurpose silicon photonics signal processor core. Nat. Commun. 8, 636 (2017).
Pérez, D., Gasulla, I. & Capmany, J. Field-programmable photonic arrays. Opt. Express 26, 27265–27278 (2018).
Zhao, Y. H. et al. On-chip programmable pulse processor employing cascaded MZI-MRR structure. Front. Optoelectron. 12, 148–156 (2019).
Khan, M. H. et al. Ultrabroad-bandwidth arbitrary radiofrequency waveform generation with a silicon photonic chip-based spectral shaper. Nat. Photonics 4, 117–122 (2010).
Tait, A. N. et al. Continuous calibration of microring weights for analog optical networks. IEEE Photonics Technol. Lett. 28, 887–890 (2016).
Tait, A. N. et al. Microring weight banks. IEEE J. Sel. Top. Quantum Electron. 22, 5900214 (2016).
Zhang, W. P. et al. Microring weight banks control beyond 8.5-bits accuracy. Preprint at https://arxiv.org/abs/2104.01164 (2021).
Tait, A. N. et al. Feedback control for microring weight banks. Opt. Express 26, 26422–26443 (2018).
Huang, C. R. et al. Demonstration of photonic neural network for fiber nonlinearity compensation in long-haul transmission systems. In Proceedings of 2020 Optical Fiber Communications Conference and Exhibition (OFC) (San Diego, CA, USA: IEEE, 2020).
Li, X. Q. et al. Performance analysis of GPU-based convolutional neural networks. In Proceedings of 2016 45th International Conference on Parallel Processing (ICPP). (Philadelphia, PA, USA: IEEE, 2016).
Zhang, Y. X. & Wang, Y. H. Nonlinear optical properties of metal nanoparticles: a review. RSC Adv. 7, 45129–45144 (2017).
He, M. B. et al. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s-1 and beyond. Nat. Photonics 13, 359–364 (2019).
Wang, Y. L. et al. Ultrahigh-speed graphene-based optical coherent receiver. Nat. Commun. 12, 5076 (2021).
Xiang, S. Y. et al. A review: Photonics devices, architectures, and algorithms for optical neural computing. J. Semiconductors 42, 023105 (2021).
Kulce, O. et al. All-optical information-processing capacity of diffractive surfaces. Light Sci. Appl. 10, 1 (2021).
Dou, H. K. et al. Residual D2NN: training diffractive deep neural networks via learnable light shortcuts. Opt. Lett. 45, 2688–2691 (2020).
Pierangeli, D. et al. Noise-enhanced spatial-photonic Ising machine. Nanophotonics 9, 4109–4116 (2020).
Fang, Y. S., Huang, J. Y. & Ruan, Z. C. Experimental observation of phase transitions in spatial photonic ising machine. Phys. Rev. Lett. 127, 043902 (2021).
Huang, J. Y., Fang, Y. S. & Ruan, Z. C. Antiferromagnetic spatial photonic Ising machine through optoelectronic correlation computing. Commun. Phys. 4, 242 (2021).
Zuo, Y. et al. All-optical neural network with nonlinear activation functions. Optica 6, 1132–1137 (2019).
Hughes, T. W. et al. Training of photonic neural networks through in situ backpropagation and gradient measurement. Optica 5, 864–871 (2018).
Zhang, H. et al. Efficient on-chip training of optical neural networks using genetic algorithm. ACS Photonics 8, 1662–1672 (2021).
Miscuglio, M. & Sorger, V. J. Photonic tensor cores for machine learning. Appl. Phys. Rev. 7, 031404 (2020).
Xie, S. N. et al. Aggregated residual transformations for deep neural networks. In Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 5987–5955 (Honolulu, HI, USA: IEEE, 2017).
Jayatilleka, H. et al. Photoconductive heaters enable control of large-scale silicon photonic ring resonator circuits. Optica 6, 84–91 (2019).
Demkov, A. A. et al. Materials for emergent silicon-integrated optical computing. J. Appl. Phys. 130, 070907 (2021).
Blumenthal, D. J. et al. Silicon nitride in silicon photonics. Proc. IEEE 106, 2209–2231 (2018).
Harris, N. C. et al. Efficient, compact and low loss thermo-optic phase shifter in silicon. Opt. Express 22, 10487–10493 (2014).
Midolo, L., Schliesser, A. & Fiore, A. Nano-opto-electro-mechanical systems. Nat. Nanotechnol. 13, 11–18 (2018).
de Lima, T. F. et al. Noise analysis of photonic modulator neurons. IEEE J. Sel. Top. Quantum Electron. 26, 7600109 (2020).
Amin, R. et al. Active material, optical mode and cavity impact on nanoscale electro-optic modulation performance. Nanophotonics 7, 455–472 (2017).
Amin, R. et al. ITO-based electro-absorption modulator for photonic neural activation function. APL Mater. 7, 081112 (2019).
Brunstein, M. et al. Excitability and self-pulsing in a photonic crystal nanocavity. Phys. Rev. A 85, 031803 (2012).
Nozaki, K. et al. Femtofarad optoelectronic integration demonstrating energy-saving signal conversion and nonlinear functions. Nat. Photonics 13, 454–459 (2019).
Ramirez, J. M. et al. III-V-on-silicon integration: from hybrid devices to heterogeneous photonic integrated circuits. IEEE J. Sel. Top. Quantum Electron. 26, 6100213 (2020).
Liu, A. Y. & Bowers, J. Photonic integration with epitaxial III–V on silicon. IEEE J. Sel. Top. Quantum Electron. 24, 6000412 (2018).
Liang, D. et al. Hybrid integrated platforms for silicon photonics. Materials 3, 1782–1802 (2010).
Selmi, F. et al. Relative refractory period in an excitable semiconductor laser. Phys. Rev. Lett. 112, 183902 (2014).
Peng, H. T. et al. Neuromorphic Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 24, 6101715 (2018).
Nahmias, M. A. et al. A laser spiking neuron in a photonic integrated circuit. Preprint at https://arxiv.org/abs/2012.08516 (2020).
Tait, A. N. et al. Silicon photonic modulator neuron. Phys. Rev. Appl. 11, 064043 (2019).
George, J. K. et al. Neuromorphic photonics with electro-absorption modulators. Opt. Express 27, 5181–5191 (2019).
Williamson, I. A. D. et al. Reprogrammable electro-optic nonlinear activation functions for optical neural networks. IEEE J. Sel. Top. Quantum Electron. 26, 7700412 (2020).
Miscuglio, M. et al. All-optical nonlinear activation function for photonic neural networks [Invited]. Optical Mater. Express 8, 3851–3863 (2018).
Huang, C. R. et al. Programmable silicon photonic optical thresholder. IEEE Photonics Technol. Lett. 31, 1834–1837 (2019).
Huang, C. R. et al. On-chip programmable nonlinear optical signal processor and its applications. IEEE J. Sel. Top. Quantum Electron. 27, 6100211 (2021).
Jha, A., Huang, C. R. & Prucnal, P. R. Reconfigurable all-optical nonlinear activation functions for neuromorphic photonics. Opt. Lett. 45, 4819–4822 (2020).
Chakraborty, I. et al. Toward fast neural computing using all-photonic phase change spiking neurons. Sci. Rep. 8, 12980 (2018).
Crnjanski, J. et al. Adaptive sigmoid-like and PReLU activation functions for all-optical perceptron. Opt. Lett. 46, 2003–2006 (2021).
Xiang, S. Y. et al. Training a multi-layer photonic spiking neural network with modified supervised learning algorithm based on photonic STDP. IEEE J. Sel. Top. Quantum Electron. 27, 7500109 (2021).
Zhang, Y. H. et al. All-optical neuromorphic binary convolution with a spiking VCSEL neuron for image gradient magnitudes. Photonics Res. 9, B201–B209 (2021).
Shi, B. et al. Multi-wavelength, multi-level inputs for an all-optical SOA-based neuron. In Proceedings of the CLEO: Science and Innovations 2021. (San Jose, California, United States: Optical Society of America, 2021).
Shi, B. et al. Lossless monolithically integrated photonic InP neuron for all-optical computation. In Proceedings of 2020 Optical Fiber Communications Conference and Exhibition (OFC). (San Diego, CA, USA: IEEE, 2020).
Mourgias-Alexandris, G. et al. An all-optical neuron with sigmoid activation function. Opt. Express 27, 9620–9630 (2019).
Shi, B., Calabretta, N. & Stabile, R. Deep neural network through an InP SOA-based photonic integrated cross-connect. IEEE J. Sel. Top. Quantum Electron. 26, 7701111 (2020).
Vandoorne, K. et al. Parallel reservoir computing using optical amplifiers. IEEE Trans. Neural Netw. 22, 1469–1481 (2011).
Vandoorne, K. et al. Experimental demonstration of reservoir computing on a silicon photonics chip. Nat. Commun. 5, 3541 (2014).
Nahmias, M. A. et al. Neuromorphic photonics. Opt. Photonics N. 29, 34–41 (2018).
Friedman, J. H. & Popescu, B. E. Gradient directed regularization for linear regression and classification. (Stanford University, 2004).
Ying, Z. F. et al. Electronic-photonic arithmetic logic unit for high-speed computing. Nat. Commun. 11, 7801311 (2020).
Cheng, J. W. et al. On-chip photonic convolutional accelerator for image processing. In Proceedings of the 26th Optoelectronics and Communications Conference 2021. (Hong Kong, China: OSA, 2021).
Lucas, A. Ising formulations of many NP problems. Front. Phys. 2, 5 (2014).
Ying, Z. F. et al. Sequential logic and pipelining in chip-based electronic-photonic digital computing. IEEE Photonics J. 12, 7801311 (2020).
Tait, A. N. Silicon photonic neural networks. PhD thesis, Princeton University, Princeton, 2018.
Nahmias, M. A. et al. Photonic multiply-accumulate operations for neural networks. IEEE J. Sel. Top. Quantum Electron. 26, 7701518 (2020).
Jouppi, N. P. et al. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the 44th annual international symposium on computer architecture. 1–12 (Toronto, ON, Canada: ACM, 2017).
Ankit, A. et al. PUMA: A programmable ultra-efficient memristor-based accelerator for machine learning inference. In Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems. 715–731 (Providence, RI, USA: ACM, 2019).
Shafiee, A. et al. ISAAC: A convolutional neural network accelerator with in-situ analog arithmetic in crossbars. ACM SIGARCH Computer Architecture N. 44, 14–26 (2016).
Ward-Foxton, S. Mythic Resizes its AI Chip. at https://www.eetimes.com/mythic-resizes-its-analog-ai-chip/.
Acknowledgements
Chaoran Huang would like to thank Alexander Tait, Bhavin Shastri and Paul Prucnal for the fruitful discussions. J.J.D. acknowledges the support of the National Key Research and Development Project of China (2018YFB2201901) and the National Natural Science Foundation of China (61805090, 62075075).
Author information
Authors and Affiliations
Contributions
H.L.Z. and J.J.D. proposed the framework of this review. All the authors contributed to the review materials.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interest.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhou, H., Dong, J., Cheng, J. et al. Photonic matrix multiplication lights up photonic accelerator and beyond. Light Sci Appl 11, 30 (2022). https://doi.org/10.1038/s41377-022-00717-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41377-022-00717-8
This article is cited by
-
Large-scale optical switches by thermo-optic waveguide lens
PhotoniX (2024)
-
Multimodal deep learning using on-chip diffractive optics with in situ training capability
Nature Communications (2024)
-
Correlated optical convolutional neural network with “quantum speedup”
Light: Science & Applications (2024)
-
Analog spatiotemporal feature extraction for cognitive radio-frequency sensing with integrated photonics
Light: Science & Applications (2024)
-
Harnessing the capabilities of VCSELs: unlocking the potential for advanced integrated photonic devices and systems
Light: Science & Applications (2024)