Abstract
In single microdisks, embedded active emitters intrinsically affect the cavity modes of the microdisks, resulting in trivial symmetric backscattering and low controllability. Here we demonstrate macroscopic control of the backscattering direction by optimizing the cavity size. The signature of the positive and negative backscattering directions in each single microdisk is confirmed with two strongly coupled microdisks. Furthermore, diabolical points are achieved at the resonance of the two microdisks, which agrees well with theoretical calculations considering the backscattering directions. Diabolical points in active optical structures pave the way for an implementation of quantum information processing with geometric phase in quantum photonic networks.
Similar content being viewed by others
Introduction
Diabolical points (DPs) and exceptional points (EPs) describe degeneracies of systems depending on parameters1,2. EPs refer to degeneracies of non-Hermitian systems with coalescent eigenstates, which are quite popular in systems with gain and loss such as parity-time-symmetric systems3,4,5. DPs indicate the degeneracy of a Hermitian system with twofold orthogonal eigenstates. Compared to EPs with gain and loss, DPs have more practical feasibility, provide a geometric phase with a controlled phase shift, and introduce new approaches to the study of topological or quantum DP behaviors6,7,8,9,10,11. Thus photons in photonic structures at DPs have potential applications in quantum information and quantum computation12,13,14,15. Meanwhile, active emitters in photonic structures are essential for a coherent electron–photon interface to implement quantum information processing in a quantum photonic network16,17,18,19,20. However, the DPs or EPs of backscattering in optics can be achieved in optical structures with a few individually controlled defects or scatterers21,22,23. In active cavities with multiple quantum emitters, the quantum emitters affect the cavity mode as scatterers themselves24,25. The random positions of multiple emitters make the system difficult to control. More importantly, multiple scatterers result in symmetric backscattering in a single microdisk26,27. Symmetric backscattering forbids a degeneracy with only trivial eigenstates; thus a coherent interface between electrons and photons at DPs is difficult to achieve.
Single microdisks have two-dimensional Hamiltonians based on clockwise (CW) and counterclockwise (CCW) modes28. Symmetric backscattering results in splitting of the eigenstates, corresponding to the absolute value of the backscattering coupling strength. Previous studies on active microdisks mainly focused on the splitting in the spectrum, and further investigations have been limited by low controllability29,30,31. In contrast, two strongly coupled microdisks have supermodes with four-dimensional Hamiltonians. The detuning between the microdisks can be controlled, and not only the absolute value but also the sign of the backscattering coupling strength can be investigated. This feature makes coupled cavities a good platform for studying the fundamental physics of backscattering in active microdisks.
Here we demonstrate Hermitian degeneracy at DPs in two coupled microdisks with embedded quantum dots (QDs). Despite the low controllability originating from the randomly positioned QDs, macroscopic control by the cavity size is achieved based on the competition between the backscattering from QDs and defects31. Then the sign of the backscattering coupling strength is investigated via the coupling between the cavities. A balanced competition is clearly demonstrated by the distributed backscattering coupling strength from negative to positive values. Furthermore, the balanced competition provides the basis for the observation of Hermitian degeneracy at DPs, which occurs when the backscattering coupling strengths in two microdisks are opposite. Our work demonstrates DPs in active optical structures. The coupled cavities pave the way for scaling up quantum information processing32,33,34, and the QDs can serve as quantum emitters if brought into resonance with the cavity modes. Therefore, our work provides a potential approach to integrate photons at DPs into a quantum network in the future.
Results
Concept and design
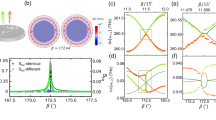
Two coupled microdisks (A and B) without backscattering have two eigenstates, as shown in Fig. 1a. For the perfect single microdisk A (B), the eigenstate is a(b) with the eigenvalue ωa(ωb). When two microdisks are coupled, there is a coupling strength g between them. When two microdisks are on resonance ωa = ωb, the two eigenstates are \(\psi = \left( {a \pm b} \right)/\sqrt 2\). For active microdisks with multiple scatterers, the degeneracy of the eigenstates of a single microdisk is lifted by backscattering. The CW and CCW modes of the single microdisk A (B) are acw,ccw (bcw,ccw), respectively. The backscattering in each cavity is symmetric between the CW and CCW modes, with strengths of Ja for microdisk A and Jb for microdisk B. The frequencies of the cavity modes ωa,b and the backscattering Ja,b can contain an imaginary part corresponding to energy loss21,25. The coupling between the cavities is only allowed between states with the same propagation directions (acw and bccw, accw and bcw) with strength g35. Owing to the backscattering, the two pairs of originally degenerate reversal states ψ1,3 and ψ2,4 (Fig. 1a) now couple to each other, resulting in new eigenstates.
The Hamiltonian on resonance (ωa,b is set to 0 for brevity) with the basis vector ψi is
where the order of the basis in the matrix is ψ1 to ψ4. Figure 1b shows the calculated eigenvalues with real backscattering coupling strengths. As shown in the Hamiltonian above, the internal coupling of the system is significantly affected by the sign of the backscattering coupling strength. When Ja = Jb (pink lines), the system is highly symmetric, and the coupling occurs between the reversal states, as shown in Fig. 1a. When Ja = −Jb (green lines), the coupling between the reversal states is destructive and only occurs between ψ1 and ψ4 or between ψ2 and ψ3. Eigenstates without reversal symmetry in the system with reversal symmetry indicate spontaneous symmetry breaking36. Furthermore, the system only has two eigenvalues, corresponding to Hermitian degeneracy at the DPs.
The degenerate eigenspace at the DPs is an important feature, providing the basis for quantum states with continuous phases. The eigenstates can also be expressed by phases \(\theta _a,\;\phi _a,\;\theta _b,\;\phi _b,\;\phi _1,\;{\mathrm{and}}\;\phi _2\) as
In this form, the phase of the left microdisk is defined by the normalized amplitudes of acw and accw with θa and ϕa. The normalized amplitude of acw is \({\mathrm{sin}} \, \theta _a{\mathrm{e}}^{i\phi _a/2},\) and the normalized amplitude of accw is \({\mathrm{cos}} \, \theta _a{\mathrm{e}}^{ - i\phi _a/2}\) 37,38. Similarly, the phase of the right microdisk is defined by θb and ϕb, where the normalized amplitude of bccw is \({\mathrm{sin}} \, \theta _b{\mathrm{e}}^{i\phi _b/2}\) and the normalized amplitude of bcw is \({\mathrm{cos}} \, \theta _b{\mathrm{e}}^{ - i\phi _b/2}\). The twofold degeneracy in the four-dimensional Hamiltonian results in two two-dimensional eigenspaces, and the reduced degrees of freedom result in correlation between the phases of the two microdisks. Figure 2a shows one eigenspace at the DP, and the correlation is \(\tan \theta _b = \left( {\tan \theta _a - \sin \gamma } \right)/\left( {1 - \tan \theta _a\sin \gamma } \right)\), where tanγ = J/g. Figure 2b shows the advantage of DPs with the phase shift by a comparison between different cases. Without degeneracy, the system is trivial (nondegenerate) and only permitted at the black dots. The blue line refers to the eigenspace at the DP without backscattering, which is linear with no phase change between two microdisks. The solid (dashed) red line refers to a point in the upper (bottom) green line in Fig. 1b at the DP with backscattering. The nonlinear correlations result in a phase shift between two microdisks, which is potentially applicable to quantum networks. For example, if waveguides are coupled to the microdisks, the phases of the CW and CCW modes in the microdisks are related to the forward and backward signals in the waveguides. Thus the coupled microdisks at the DP can be used for the phase shift of a signal in two waveguides as a quantum node. Meanwhile, γ(g) can be controlled by the gap between the two microdisks but does not affect the DP (Ja = −Jb), indicating more potential applications such as controllable directional lasers. More detailed calculations can be found in Supplementary Information.
a One eigenspace with different values of γ, Ja = −Jb = J and ϕa = ϕb = 0. This eigenspace refers to the upper green line in Fig. 1 b. b Eigenspaces and correlations between two microdisks. The black dots refer to trivial systems. The blue line refers to a DP without backscattering. The red lines refer to two DPs with backscattering for γ = 0.30 π with a phase shift. The solid red line corresponds to the red line in (a) and a point in the upper green line in Fig. 1 (b). The dashed red line corresponds to a point in the bottom green line in Fig. 1 (b).
Macroscopic control to achieve DPs
In an experiment, microdisks with a radius of 1 μm were fabricated on a 250-nm-thick GaAs slab. One layer of InAs QDs was grown in the center of the slab with a density of 30 μm−2. The gap between the microdisks was designed to range from 50 to 130 nm. Figure 3a shows scanning electron microscopic (SEM) images of the cavities. The QDs were excited by a laser with a wavelength of 532 nm at 4.2 K. Figure 3b shows two spectrally resolved peaks resulting from backscattering in a single microdisk. The cavity modes are redshifted by 7 nm by the thermo-optic effect with increasing excitation power39. Meanwhile, the splitting and peak linewidths are barely affected, as shown in Fig. 3c. Therefore, the detuning between the two microdisks can be controlled by a selective excitation.
a SEM images of a single microdisk and double microdisks. The excitation laser is labeled by the green arrow. b The redshift of the cavity modes with increasing excitation power. c The wavelengths, linewidths, and splitting between the two peaks extracted from Lorentzian multipeak fitting. d Statistics of the linewidth differences between the split modes. The resolution of the spectrometer is 0.1 nm. e Statistics of the splitting. A splitting of 1000 μeV corresponds to 0.80 nm at a wavelength of 1000 nm. f Distribution of the splitting and half-Gaussian fitting.
For the two coupled microdisks, the DPs require ωa = ωb and Ja = −Jb for both the real and imaginary parts. In realistic active microdisks, the backscattering is difficult to precisely control. The approaches used to control backscattering in passive microdisks are invalid here due to the randomly positioned QDs. Instead, the devices are designed to improve the possibility of DPs. The possibility of equal imaginary parts of ωa,b (linewidth) is improved by the identical design and fabrication of the two coupled microdisks. The linewidth difference between the two split modes, which is the imaginary part of J, is smaller than the resolution of our spectrometer, as shown in Fig. 3d. The linewidth difference (average value of 0.02 nm) is also much smaller than the mode splitting (average value of 0.24 nm as shown in Fig. 3e), which represents the real part of J. Thus the imaginary part of Ja,b is almost zero. The symmetric backscattering and the very small imaginary part can be attributed to an average effect of randomly positioned multiple scatterers, as discussed in Supplementary Information. Then the main challenge for the DPs is to control the system toward opposite real parts of the backscattering coupling strength Ja = −Jb. To solve the problem of low controllability, we propose to use macroscopic control based on the competition between different types of scatterers.
The microdisk contains two types of scatterers. One type is the defects on the surface, and the other type is the embedded QDs40,41. Although the detailed distribution of defects and QDs is random, the main role of the two types of scatterers is related to the perimeter/area ratio determined by the microdisk size. Previous studies mainly focused on splitting in single microdisks, corresponding to the absolute value of the backscattering coupling strength29,30,31. Thus the competition between the two types of scatterers was only qualitatively described31. In contrast, the competition here is further investigated, including the sign of the backscattering coupling strength. The backscattering of the scatterers is related to the difference between the dielectric permittivities of the scatterers and the surrounding medium21,25,29. Defects serve as low-refractive-index scatterers with positive contributions to J, and conversely, QDs serve as high-refractive-index scatterers with negative contributions. Thus the sign of the backscattering coupling strength is affected by the dominant type of scatterers. When the competition is balanced, both positive and negative values of J can be predicted from the distribution, paving the way for DPs at Ja = −Jb. Based on the results in previous work31 and the parameters of our devices, the microdisk radius is designed to be 1 μm for balanced competition. Figure 3e, f show the statistics of the splitting 2|J| with a nearly half-Gaussian distribution, corresponding to a Gaussian distribution of J with a mean value close to zero. This result demonstrates good balance in the competition. More design and fabrication details are shown in Supplementary Information.
Excitation-power-dependent photoluminescence (PL) spectroscopy by a selective excitation was performed on various coupled microdisks. Figure 4 shows four typical PL mappings of supermodes as well as theoretical fits (solid lines). Two anti-crossings (yellow arrows) indicating strong couplings between the supermodes (one pair of green lines and another pair of gray lines) are observed in all measurements. The two and only two anti-crossings are the result of symmetric backscattering. More detailed discussions and additional data are shown in Supplementary Information. Figure 4a shows the case for Ja = 0 and Jb ≠ 0, which means that splitting in the first microdisk is not observed. Figure 4b, c shows the case for JaJb > 0, which means that the backscattering coupling strengths in the two microdisks are both positive or both negative. In particular, Fig. 4c shows the case for Ja = Jb, which results in two simultaneous anti-crossings on resonance (purple dashed line). Figure 4d shows the remarkable case with Hermitian degeneracy at the DPs, where Ja = −Jb. Strong couplings occur between the different pairs of supermodes compared to the coupling behaviors of two pairs of supermodes in Fig. 4b, c, which is the key difference between the cases with JaJb > 0 and JaJb < 0. The different couplings refer to the significance of the sign of the backscattering coupling strength in coupled cavities, in contrast to previous work where only the absolute value is characterized by resolving the splitting in single cavities29,30,31.
Discussion
The fitted results in Fig. 4d show a coupling strength of g = 145 μeV and Ja = −Jb = 200 μeV. The linewidths of all four peaks are approximately 0.20 nm. This means that the two cavities are brought into resonance, where ωa = ωb for both the real and imaginary parts. Meanwhile, the same linewidth of the two peaks from the single microdisks indicates that the imaginary parts of Ja and Jb are zero. Therefore, the Hermitian degeneracy and DPs on resonance (purple dashed line) are demonstrated, in good agreement with the theoretical result shown by the green lines in Fig. 1b. The eigenstates split by the backscattering in the single microdisks are degenerate because of the coupling between the two microdisks. The ratio of the backscattering coupling strength to the coupling strength between the microdisks is J/g = 1.38 = tan(0.30π). Thus the two Hermitian degeneracies correspond to two paths, as shown by the red lines in Fig. 2b. The achieved DPs demonstrate the potential of macroscopic control in active microdisks with multiple QDs. In addition, as fabrication technology and QD growth techniques improve42,43 and g is controlled by a tunable gap44,45, backscattering in coupled active cavities may also be precisely controlled in the future.
In summary, we have demonstrated DPs in two strongly coupled active microdisks. The coupling between the cavities reveals that the sign of the backscattering coupling strength is an important physical property. Macroscopic control of the backscattering is achieved based on a competition between defects and emitters, solving the problem of low controllability originating from randomly positioned scatterers. The competition is balanced by an optimized microdisk size and experimentally demonstrated, providing the basis for the successful observation of DPs. This work paves the way for DPs or EPs in optical structures with active emitters and thus has potential for applications in quantum photonic networks. In addition to individual quantum devices46,47,48,49, coupled cavities can also be designed with more exotic phenomena and applications.
Materials and methods
Growth of the sample with QDs
The sample for our device was grown by molecular beam epitaxy, which consists of a 250-nm-thick GaAs slab, a 1-μm-thick AlGaAs sacrificial layer, and a GaAs substrate. One layer of self-assembled QDs was grown at a low growth rate to achieve a low density and a large dot size in the middle of the GaAs slab. The QD density is approximately 30 μm−2. One ground state and at least two excited states could be observed from the PL spectrum of ensemble QDs. The wavelength of the ground state is approximately 1200 nm, and the wavelength of the first excited state is approximately 1120 nm.
Microdisk fabrication
Microdisks were fabricated by employing electron beam lithography to pattern the resist, followed by dry etching using induced coupled plasma to form circular pillars. Then wet etching using hydrofluoric acid solutions was performed to dissolve the sacrificial layer and form a supporting pillar. The gaps between the two microdisks were designed to range from 50 to 130 nm.
Optical measurement
The optical measurement was implemented with a conventional confocal microPL system. The device was mounted on a three-dimensional nanopositioner and cooled down to 4.2 K by exchanging helium gas with a helium bath. A solid-state laser with an emission wavelength at 532 nm was first used to selectively excite and heat one of the microdisks. The excited GaAs substrate then excites the wetting layer below the QDs, and the QDs are subsequently excited. Finally, all the cavity modes were excited by the QDs within their spectral range of emission. Owing to the random emission direction of the QDs, the QDs will not selectively excite CW or CCW modes. The PL spectra were collected by a linear array of InGaAs detectors dispersed through a spectrometer with a resolution of 0.1 nm.
Data availability
The data that support the plots within this paper and Supplementary Information are available from the corresponding author upon request.
References
Berry, M. V. & Wilkinson, M. Diabolical points in the spectra of triangles. Proc. R. Soc. A Math. Phys. Eng. Sci. 392, 15–43 (1984).
Keck, F., Korsch, H. J. & Mossmann, S. Unfolding a diabolic point: a generalized crossing scenario. J. Phys. A Math. Gen. 36, 2125 (2003).
Jing, H. et al. PT-symmetric phonon laser. Phys. Rev. Lett. 113, 053604 (2014).
Lü, H. et al. Exceptional points in random-defect phonon lasers. Phys. Rev. Appl. 8, 044020 (2017).
Zhang, J. et al. A phonon laser operating at an exceptional point. Nat. Photonics 12, 479–484 (2018).
Nikam, R. S. & Ring, P. Manifestation of the Berry phase in diabolic pair transfer in rotating nuclei. Phys. Rev. Lett. 58, 980–983 (1987).
Bruno, P. Berry phase, topology, and degeneracies in quantum nanomagnets. Phys. Rev. Lett. 96, 117208 (2006).
Estrecho, E. et al. Visualising Berry phase and diabolical points in a quantum exciton-polariton billiard. Sci. Rep. 6, 37653 (2016).
Lee, T. E., Reiter, F. & Moiseyev, N. Entanglement and spin squeezing in non-Hermitian phase transitions. Phys. Rev. Lett. 113, 250401 (2014).
Huang, R. et al. Nonreciprocal photon blockade. Phys. Rev. Lett. 121, 153601 (2018).
Wu, Y. et al. Observation of parity-time symmetry breaking in a single-spin system. Science 364, 878–880 (2019).
Avron, J. E., Raveh, A. & Zur, B. Adiabatic quantum transport in multiply connected systems. Rev. Mod. Phys. 60, 873–915 (1988).
Jones, J. A. et al. Geometric quantum computation using nuclear magnetic resonance. Nature 403, 869–871 (2000).
Duan, L. M., Cirac, J. I. & Zoller, P. Geometric manipulation of trapped ions for quantum computation. Science 292, 1695–1697 (2001).
Laing, A. et al. Observation of quantum interference as a function of Berry’s phase in a complex Hadamard optical network. Phys. Rev. Lett. 108, 260505 (2012).
Imamoḡlu, A. et al. Quantum information processing using quantum dot spins and cavity QED. Phys. Rev. Lett. 83, 4204–4207 (1999).
Vahala, K. J. Optical microcavities. Nature 424, 839–846 (2003).
Reiserer, A. & Rempe, G. Cavity-based quantum networks with single atoms and optical photons. Rev. Mod. Phys. 87, 1379–1418 (2015).
Qian, C. J. et al. Two-photon Rabi splitting in a coupled system of a nanocavity and exciton complexes. Phys. Rev. Lett. 120, 213901 (2018).
Qian, C. J. et al. Enhanced strong interaction between nanocavities and p-shell excitons beyond the dipole approximation. Phys. Rev. Lett. 122, 087401 (2019).
Mazzei, A. et al. Controlled coupling of counterpropagating whispering-gallery modes by a single Rayleigh scatterer: a classical problem in a quantum optical light. Phys. Rev. Lett. 99, 173603 (2007).
Chen, W. J. et al. Exceptional points enhance sensing in an optical microcavity. Nature 548, 192–196 (2017).
Kim, M. et al. Partially directional microdisk laser with two Rayleigh scatterers. Opt. Lett. 39, 2423–2426 (2014).
Kippenberg, T. J., Spillane, S. M. & Vahala, K. J. Modal coupling in traveling-wave resonators. Opt. Lett. 27, 1669–1671 (2002).
Zhu, J. G. et al. On-chip single nanoparticle detection and sizing by mode splitting in an ultrahigh-Q microresonator. Nat. Photonics 4, 46–49 (2010).
Yi, X. et al. Multiple-Rayleigh-scatterer-induced mode splitting in a high-Q whispering-gallery-mode microresonator. Phys. Rev. A 83, 023803 (2011).
He, L. N. et al. Statistics of multiple-scatterer-induced frequency splitting in whispering gallery microresonators and microlasers. N. J. Phys. 15, 073030 (2013).
Song, Q. H. Emerging opportunities for ultra-high Q whispering gallery mode microcavities. Sci. China Phys. Mech. Astron. 62, 74231 (2019).
Hiremath, K. R. & Astratov, V. N. Perturbations of whispering gallery modes by nanoparticles embedded in microcavities. Opt. Express 16, 5421–5426 (2008).
Li, Q. et al. Azimuthal-order variations of surface-roughness-induced mode splitting and scattering loss in high-Q microdisk resonators. Opt. Lett. 37, 1586–1588 (2012).
Jones, B. D. et al. Splitting and lasing of whispering gallery modes in quantum dot micropillars. Opt. Express 18, 22578–22592 (2010).
Stannigel, K. et al. Optomechanical transducers for long-distance quantum communication. Phys. Rev. Lett. 105, 220501 (2010).
Lodahl, P., Mahmoodian, S. & Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 87, 347–400 (2015).
Zhao, Y. H. et al. Ultrafast optical switching using photonic molecules in photonic crystal waveguides. Opt. Express 23, 9211–9220 (2015).
Schmidt, C. et al. Observation of optical coupling in microdisk resonators. Phys. Rev. A 80, 043841 (2009).
Miransky, V. A. Dynamical Symmetry Breaking in Quantum Field Theories (World Scientific, Singapore, 1994).
Malzard, S., Poli, C. & Schomerus, H. Topologically protected defect states in open photonic systems with non-Hermitian charge-conjugation and parity-time symmetry. Phys. Rev. Lett. 115, 200402 (2015).
Longhi, S. & Feng, L. Unidirectional lasing in semiconductor microring lasers at an exceptional point [Invited]. Photonics Res. 5, B1–B6 (2017).
Benyoucef, M. et al. Strongly coupled semiconductor microcavities: a route to couple artificial atoms over micrometric distances. Phys. Rev. B 77, 035108 (2008).
Stangl, J., Holý, V. & Bauer, G. Structural properties of self-organized semiconductor nanostructures. Rev. Mod. Phys. 76, 725–783 (2004).
Tuomisto, F. & Makkonen, I. Defect identification in semiconductors with positron annihilation: experiment and theory. Rev. Mod. Phys. 85, 1583–1631 (2013).
Kojima, T. et al. Accurate alignment of a photonic crystal nanocavity with an embedded quantum dot based on optical microscopic photoluminescence imaging. Appl. Phys. Lett. 102, 011110 (2013).
Gschrey, M. et al. Highly indistinguishable photons from deterministic quantum-dot microlenses utilizing three-dimensional in situ electron-beam lithography. Nat. Commun. 6, 7662 (2015).
Lin, H. et al. Strong coupling of different cavity modes in photonic molecules formed by two adjacent microdisk microcavities. Opt. Express 18, 23948–23956 (2010).
Du, H. et al. Precise control of coupling strength in photonic molecules over a wide range using nanoelectromechanical systems. Sci. Rep. 6, 24766 (2016).
Greentree, A. D. et al. Quantum phase transitions of light. Nat. Phys. 2, 856–861 (2006).
Dousse, A. et al. Ultrabright source of entangled photon pairs. Nature 466, 217–220 (2010).
Liew, T. C. H. & Savona, V. Single photons from coupled quantum modes. Phys. Rev. Lett. 104, 183601 (2010).
Bose, R. et al. All-optical coherent control of vacuum Rabi oscillations. Nat. Photonics 8, 858–864 (2014).
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant No. 11934019, No. 11721404, No. 51761145104, No. 61675228, and No. 11874419; the Ministry of Science and Technology of China under Grant No. 2016YFA0200400; the Strategic Priority Research Program under Grant No. XDB07030200, No. XDB28000000, and No. XDB07020200; the Instrument Developing Project under Grant No. YJKYYQ20180036; the Interdisciplinary Innovation Team of the Chinese Academy of Sciences; and the Key R&D Program of Guangdong Province under Grant No. 2018B030329001. The authors would like to thank Gas Sensing Solutions Ltd. for the MBE equipment.
Author information
Authors and Affiliations
Contributions
X. Xu conceived and planned the project. J.Y., C.Q., and X. Xie designed and fabricated the devices. J.Y., C.Q., X. Xie, K.P., S.W., F.S., S. Sun, J.D., Y.Y., S. Shi, J.H., and X. Xu performed the optical measurement. M.J.S. and I.G.T. grew the quantum dot wafer. All authors discussed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, J., Qian, C., Xie, X. et al. Diabolical points in coupled active cavities with quantum emitters. Light Sci Appl 9, 6 (2020). https://doi.org/10.1038/s41377-020-0244-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41377-020-0244-9
This article is cited by
-
Non-orthogonal cavity modes near exceptional points in the far field
Communications Physics (2024)
-
Exceptional points and non-Hermitian photonics at the nanoscale
Nature Nanotechnology (2023)
-
Low-threshold topological nanolasers based on the second-order corner state
Light: Science & Applications (2020)