Abstract
For 4d1 and 5d1 spin–orbit-coupled electron configurations, the notion of nonmagnetic j=3/2 quartet ground state discussed in classical textbooks is at odds with the observed variety of magnetic properties. Here we throw fresh light on the electronic structure of 4d1 and 5d1 ions in molybdenum- and osmium-based double-perovskite systems and reveal different kinds of on-site many-body physics in the two families of compounds: although the sizable magnetic moments and g-factors measured experimentally are due to both metal d–ligand p hybridisation and dynamic Jahn–Teller interactions for 4d electrons, it is essentially d−p covalency for the 5d1 configuration. These results highlight the subtle interplay of spin–orbit interactions, covalency and electron–lattice couplings as the major factor in deciding the nature of the magnetic ground states of 4d and 5d quantum materials. Cation charge imbalance in the double-perovskite structure is further shown to allow a fine tuning of the gap between the t2g and eg levels, an effect of much potential in the context of orbital engineering in oxide electronics.
Similar content being viewed by others
Introduction
A defining feature of d-electron systems is the presence of sizable electron correlations, also referred to as Mott–Hubbard physics. The latter has been traditionally associated with first-series (3d) transition-metal (TM) oxides. But recently one more ingredient entered the TM oxide ‘Mottness’ paradigm—large spin–orbit couplings (SOCs) in 4d and 5d quantum materials.1,2 It turns out that for specific t2g-shell electron configurations, a strong SOC can effectively augment the effect of Hubbard correlations:1 although the 4d and 5d orbitals are relatively extended objects and the Coulomb repulsive interactions are weakened as compared with the more compact 3d states, the spin–orbit-induced level splittings can become large enough to break apart the ‘nonrelativistic’ t2g bands into sets of well-separated, significantly narrower subbands for which even a modest Hubbard U acting on the respective Wannier orbitals can then open up a finite Mott–Hubbard-like gap.1 On top of that, SOC additionally reshuffles the intersite superexchange.3 The surprisingly large anisotropic magnetic interactions that come into play via the strong SOCs in iridates,3–8 e.g., are responsible for an exotic assortment of novel magnetic ground states and excitations.2,3,9
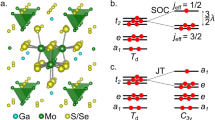
For large t2g−eg splittings, the spin–orbit-coupled and electron configurations can be in first approximation viewed as ‘complementary’: in the simplest picture, the d-shell manifold can be shrunk to the set of j=1/2 and j=3/2 relativistic levels, with a j=3/2 ground state for the TM configuration and a j=1/2 ground state for .10–12 Although strongly spin–orbit-coupled oxides and halides—iridates, rhodates and ruthenates, in particular—have generated substantial experimental and theoretical investigations in recent years, much of the properties of 5d and 4d systems remain to large extent unexplored.
From textbook arguments,10–12 the j=3/2 quadruplet should be characterised by a vanishing magnetic moment in cubic symmetry, due to perfect cancellation of the spin and angular momentum contributions. But this assertion leaves unexplained the wide variety of magnetic properties recently found in 4d1 and 5d1 cubic oxide compounds.13–20 Ba2YMoO6, e.g., develops no magnetic order despite a Curie–Weiss temperature of ≈−200 K (refs 13,14) and features complex magnetic dynamics that persists down to the mK range, possibly due to either a valence-bond-glass15 or spin-liquid16 ground state. Also, Ba2NaOsO6 displays an antiferromagnetic Curie–Weiss temperature18,19 but orders ferromagnetically below 7 K (ref. 20), whereas Ba2LiOsO6 is a spin-flop antiferromagnet.20
Here we carry out a detailed ab initio investigation of the Mo5+ 4d1 and Os7+ 5d1 relativistic electronic structure in the double-perovskite compounds Ba2YMoO6, Ba2LiOsO6 and Ba2NaOsO6. In addition to providing reliable results for the energy scale of the d-level splittings, t2g−eg and induced by SOC within the manifold, we analyse the role of TM d−O p orbital mixing plus the strength of electron–lattice couplings. It is found that strong metal d−O p hybridisation generates a finite magnetic moment even for perfectly cubic environment around the TM site, providing ab initio support to the phenomenological covalency factor introduced in this context by Stevens.21 The TM d1 magnetic moment is further enhanced by tetragonal distortions, against which the octahedral oxygen cage is unstable. According to our results, such Jahn–Teller (JT) effects are particularly strong for the Mo 4d1 ions in Ba2YMoO6. Although additional investigations are needed for clarifying the role of intersite cooperative couplings,22,23 our calculations emphasise the high sensitivity of the effective magnetic moments to both metal–ligand covalency effects and local JT physics. The material dependence for the ratio among the strengths of the spin–orbit interaction, the JT coupling parameter and the effective covalency factor that we compute here provide a solid basis for future studies addressing the role of intersite interactions on the double-perovskite fcc lattice.
Results
Quantum chemistry calculations were first performed to resolve the essential features of the electronic structure of the cubic lattice configuration, without accounting for electron–lattice couplings (see Materials and methods for computational details and Figure 1 for a sketch of a three-dimensional double-perovskite crystal). Results for the splitting between the Mo5+ j=3/2 and j=1/2 spin–orbit states, Δ3/2→1/2, are provided in Table 1 at two levels of approximation, i.e., multiconfiguration complete-active-space self-consistent field (CASSCF) and multireference configuration interaction (MRCI) with single and double excitations on top of the CASSCF wave function.24 Knowing the splitting Δ3/2→1/2, the strength of the SOC parameter can be easily derived as .11 The resulting λ of 89 meV is somewhat smaller than earlier estimates of 99 meV for Mo5+ impurities in SrTiO3.25 A most interesting finding, however, is that despite the cubic environment the quantum chemistry calculations yield a nonvanishing magnetic moment and a finite g-factor. This obviously does not fit the nonmagnetic j=3/2 quartet ground state assumed to arise in standard textbooks on crystal-field theory11,12 from exact cancellation between the spin and the orbital moments.
Sketch of the atomic positions in a cubic double-perovskite compound, Ba2BB′O6. B stands here for Y, Na or Li (site at the centre of a dark-blue octahedron); B′ is either Mo or Os (site at the centre of a light-green octahedron). O ions are shown as small red spheres, whereas the Ba sites are the larger blue spheres.
At a qualitative level, it has been argued by Stevens21 that finite g-factor values can in fact occur for j=3/2 ions due to TM-O covalency on the TM O6 octahedron. For better insight into the nature of such effects, we therefore performed a simple numerical experiment in which the six ligands coordinating the reference Mo5+ 4d1 ion are replaced by −2 point charges with no atomic basis functions. In that additional set of computations the magnetic moment and the g-factor do vanish, in agreement with the purely ionic picture of Kotani, Abragam and Bleaney.10,11 This shows that one tuning knob for switching magnetism on is indeed the TM 4d−O 2p orbital hybridisation. The latter is strong for high ionisation states such as Mo5+ (as the tails of the 4d-like valence orbitals indicate in the case the nearest-neighbor ligands are provided with atomic basis sets, see Figure 2a), gives rise to partial quenching of the orbital moment and makes that the exact cancellation between the spin and the orbital moments no longer holds.
(a) Mo 4d t2g charge distribution as obtained by CASSCF calculations. The tails at the nearest-neighbor O sites have substantial weight. (b) TM t2g splittings in cubic (left) and tetragonal (right) symmetry; δ1=0 and δ2=Δ3/2→1/2 for cubic octahedra. (c) Ground-state energy as function of z axis tetragonal distortion, MRCI results both with and without spin–orbit coupling. (d) Variation of the Mo 4d1 magnetic moment (μ||) and g-factor (g||) with the amount of z axis tetragonal distortion, MRCI results including spin–orbit interactions.
We find that this effect is even stronger for the formally 7+ Os ion in Ba2LiOsO6 and Ba2NaOsO6. As shown in Table 2, g-factors as large as 0.4 are computed in this case. The quantum chemistry results also allow us to estimate the strength of the effective Os7+ 5d1 SOC constant, with , lower than λ=468 meV in tetravalent 5d5 iridates.26
As the electron configuration is susceptible to JT effects, we carried out further investigations on the stability of an ideal TM O6 octahedron against tetragonal (z axis) distortions. A total-energy profile for specified geometric configurations is provided in Figure 2c for an embedded MoO6 octahedron. It is seen that the minimum corresponds to ~3% tetragonal compression, as compared with the cubic octahedron of the Fm3m crystalline structure.14 As expected, the magnetic moment rapidly increases in the presence of distortions, as illustrated in Table 3 and Figure 2d.
Depending on further details related to the strength of the intersite couplings among ‘JT centres’, static deformations away from cubic symmetry may be realised in some systems, as observed for example in the Re6+ 5d1 double-perovskite Sr2MgReO6 (ref. 27) and rare-earth molibdates.28,29 If the local JT couplings and intersite interactions are relatively weak, one may be left on the other hand in a dynamic JT regime, as earlier pointed out for the particular configuration by, e.g., Kahn and Kettle.30 The relevant vibrational modes that couple to the 2T2g electronic term are those of Eg symmetry ((3z2−r2)- and (x2−y2)-like). From the quantum chemistry calculations, we find that the potential-energy well is significantly shallower for these normal coordinates, as compared with z axis-only compression. The value we computed for the Mo5+ ion in Ba2YMoO6, ≈40 meV, is comparable to the estimate made in the 1970s for Mo5+ t2g1 impurity ions within the SrTiO3 matrix, ≈60 meV.25 For the osmates, the depth of this potential well is much reduced, with EJT values in the range of 10–15 meV by spin–orbit MRCI calculations (Table 4).
The vibronic model of Kahn and Kettle30 provides specific expressions for the g-factors. In particular, g|| can be parametrised as30
where kcov is Stevens’ covalency factor21 and
The parameters x and ρ are defined as30 and , where is the Eg-mode vibrational energy and g⊥=0 by symmetry.11,21,30 Recent infrared transmission spectra indicate that cm−1≈70 meV for the bond-stretching phonons.17,31 The effective parameter kcov we can easily evaluate from the static g|| values obtained in the MRCI spin–orbit treatment (Tables 1 and 2) if vibronic interactions are neglected (kvib=1 for ‘frozen’ cubic octahedra), with . This yields covalency reduction factors of 0.90 for Ba2YMoO6 and 0.80 for the osmates.
Estimates for g|| are provided in Table 4, using the Kahn–Kettle vibronic model and the quantum chemistry results for λ, kcov and EJT. It is seen that a large ρ/x ratio (i.e., large λ/EJT) makes that g|| is generated mostly through covalency effects in the osmates, with minor contributions from vibronic couplings. On the other hand, the small ρ/x ratio in Ba2YMoO6 gives rise to a strong enhancement of g|| through vibronic effects, with a factor of nearly 4 between (1−kcovkvib) and (1−kcov). This way, the interesting situation arises that the TM magnetic moment is mainly due to vibronic effects in Ba2YMoO6 and predominantly to strong covalency in Ba2LiOsO6 and Ba2NaOsO6.
Discussion
Experimentally, the measured magnetic moments are indeed significantly smaller in Ba2LiOsO6 and Ba2NaOsO6 (refs 19,20) as compared with Ba2YMoO6 (refs 13,14,17,25). With regard to the estimates we make here for g||, possible sources of errors concern the accuracy of the calculated EJT when using the experimental crystal structure as reference and correlation and polarisation effects beyond a single TM O6 octahedron.32,33 The latter effects would only increase EJT. With respect to the former aspect, it is known that by advanced quantum chemistry calculations, the lattice constants of TM oxides can be computed with deviations of <0.5% from the measured values,32 which implies rather small corrections to EJT. Interestingly, recent findings of additional phonon modes at low temperatures17 indicate static distortions of the MoO6 octahedra in Ba2YMoO6 and indeed a rather large EJT. More detailed investigations on this matter are left for future work. Valuable experimental data that can be directly compared with our calculations would be the results of electron spin resonance measurements of the g-factors.
It is also worth pointing out that using the Kahn–Kettle model even a EJT of 75 meV, five to seven times larger than the values computed by MRCI for the osmates (Table 4), still yields a rather moderate g|| factor of 0.65 for the Os 5d1 ion. Such g|| factors of 0.4–0.6 compare quite well with the low-temperature magnetic moment derived from magnetisation and muon spin relaxation measurements on Ba2NaOsO6, ≈0.2 μB.19,20 For the Mo 4d1 ion in Ba2YMoO6, the computed g|| factor is much more sensitive to variations of EJT—increasing EJT from, e.g., 40–200 meV enhances g|| of Equation (1) from ≈0.6 to ≈1.6.
One other remarkable prediction of Kahn and Kettle30 is that the splitting of the j=3/2 and j=1/2 states is increased through vibronic couplings, by a factor
This effect turns out to be small in the osmates, given the small x and large ρ in those compounds. But we compute a strong modification of the j=3/2 to j=1/2 excitation energy for Ba2YMoO6, from ~0.13 eV in the absence of vibronic interactions (Table 1) to ≈0.20 eV with JT effects included (EJT=40 meV). Experimentally, the situation can be clarified by direct resonant inelastic X-ray scattering (RIXS) measurements on Ba2YMoO6. High-resolution RIXS measurements could also address the occurrence of static distortions at low temperatures, suggested for Ba2YMoO6 on the basis of extra phonon modes in the low-T infrared transmission spectra17 and for Ba2NaOsO6 from the integrated entropy through the magnetic phase transition at ~7 K.19 According to the MRCI data in Table 3, a reduction by 0.5–1.5% of the interatomic distances on one set of O–Mo–O links already gives a splitting of 20–50 meV of the low-lying spin–orbit states. Splittings of this size should be accessible with last-generation RIXS apparatus.
Also of interest is an experimental confirmation of the unusually large t2g−eg gap we predict in the double-perovskite heptavalent osmates, ≳6 eV (Table 2). According to the results of additional computations we carried out, the source of this exceptional d-level splitting is the stabilisation of the Os t2g states due to the large effective charge (formally 7+) at the nearest-neighbor Os sites. The latter are situated on the axes along which the lobes of the t2g orbitals are oriented; in contrast, the lobes of the eg functions point towards the monovalent species (Li1+ or Na1+). For example, test CASSCF calculations in which the size of the point charges placed at the 12 Os and 6 alkaline-ion nearest-neighbor sites are modified from the formal ionic values 7+ and 1+ (12×7+6×1=90) to 5+ and 5+ (12×5+6×5=90) show a reduction of about 2 eV of the t2g−eg level splitting. Similar effects, with relative shifts and even inversion of the d-electron energy levels due to charge imbalance at nearby cation sites, were recently evidenced in Sr2RhO4 and Sr2IrO4,8,26 the rare-earth 227 iridates R2Ir2O7 (ref. 34) and Cd2Os2O7.35 The mechanism has not been thoroughly explored so far experimentally but seems to hold much potential in the context of orbital engineering in TM compounds.
To summarise, it is well known that nominal orbital degeneracy gives rise in 3d TM oxides to subtle couplings between the electronic and lattice degrees of freedom and very rich physics. Here we resolve the effect of electron–lattice interactions on the magnetic properties of heavier, 4d and 5d TM ions with a formally degenerate t2g1 electron configuration in the double-perovskite materials Ba2YMoO6, Ba2LiOsO6 and Ba2NaOsO6. In particular, using advanced quantum chemistry electronic-structure calculations, we reconcile the notion of a nonmagnetic spin–orbit-coupled t2g1 j=3/2 ground state put forward by Kotani, Abragam, Bleaney and others10–12 with the variety of magnetic properties recently observed in 4d1 and 5d1 double perovskites. Our analysis shows that the sizable magnetic moments and g-factors found experimentally are due to strong TM d–ligand p hybridisation and dynamic JT effects, providing new perspectives on the interplay between metal–ligand interactions and SOCs in TM oxides. It also highlights the proper theoretical frame for addressing the remarkably rich magnetic properties of d1 double perovskites2,15,16,19,20 in particular. Over the past two decades, vibronic couplings have unjustifiably received low attention in the case of these intriguing materials.
Materials and methods
All ab initio calculations were carried out with the quantum chemistry package Molpro.36 Crystallographic data as derived in ref. 14 for Ba2YMoO6 and in ref. 18 for Ba2LiOsO6 and Ba2NaOsO6 were employed.
We used effective core potentials, valence basis functions of triple-zeta quality and two f polarisation functions for the reference Mo/Os ions37,38 for which the d-shell excitations are explicitly computed. All-electron triple-zeta basis sets supplemented with two d polarisation functions39 were applied for each of the six adjacent O ligands. The eight Ba nearest neighbours were in each case modelled by Ba2+ ‘total-ion’ pseudopotentials supplemented with a single s function.40 For Ba2YMoO6, the six nearby Y sites were described by effective core potentials and valence basis functions of double-zeta quality.37 In Ba2LiOsO6 and Ba2NaOsO6, we employed total-ion pseudopotentials for the six nearest Li and Na cations and sets of one s and one p functions.41 The farther solid-state surroundings enter the quantum chemistry calculations at the level of a Madelung ionic potential. How the complexity and accuracy of quantum chemistry calculations for an infinite solid can be systematically increased is addressed in, e.g., refs 32,33,42,43.
For the CASSCF calculations of the d-shell splittings, we used active spaces of either three (t2g) or five (t2g plus eg) orbitals. The CASSCF optimisations were carried out for an average of either the 2T2g () or 2T2g()+2E2g() eigenfunctions of the scalar relativistic Hamiltonian. All O 2p and Mo/Os 4d/5d electrons on the reference TM O6 octahedron were correlated in the MRCI treatment. The latter was performed with single and double substitutions with respect to the CASSCF reference, as described in refs 44,45. The spin–orbit treatment was carried out according to the procedure described in ref. 46.
The g-factors were computed following a scheme proposed by Bolvin47 and Vancoillie.48 For a Kramers-doublet ground state , the Abragam–Bleaney tensor11 G=ggT can be expressed in matrix form as
where ge is the free-electron g-factor and
The matrix elements of were extracted from the Molpro outputs, whereas the matrix elements of were derived using the conventional expressions for the generalised Pauli matrices:
The g-factors were calculated as the positive square roots of the three eigenvalues of G.
References
Kim, B. J. et al. Novel J eff=1/2 Mott state induced by relativistic spin-orbit coupling in Sr2IrO4 . Phys. Rev. Lett. 101, 076402 (2008).
Witczak-Krempa, W., Chen, G., Kim, Y. B. & Balents, L. Correlated quantum phenomena in the strong spin-orbit regime. Annu. Rev. Condens. Matter Phys. 5, 57–82 (2014).
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: from Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009).
Gretarsson, H. et al. Magnetic excitation spectrum of Na2IrO3 probed with resonant inelastic x-ray scattering. Phys. Rev. B 87, 220407 (2013).
Chun, S. H. et al. Direct evidence for dominant bond-directional interactions in a honeycomb lattice iridate Na2IrO3 . Nat. Phys. 11, 462–466 (2015).
Yamaji, Y., Nomura, Y., Kurita, M., Arita, R. & Imada, M. First-principles study of the honeycomb-lattice iridates Na2IrO3 in the presence of strong spin-orbit interaction and electron correlations. Phys. Rev. Lett. 113, 107201 (2014).
Katukuri, V. M. et al. Kitaev interactions between j=1/2 moments in honeycomb Na2IrO3 are large and ferromagnetic: insights from ab initio quantum chemistry calculations. New J. Phys. 16, 013056 (2014).
Bogdanov, N. A. et al. Orbital reconstruction in nonpolar tetravalent transition-metal oxide layers. Nat. Commun. 6, 7306 (2015).
Chaloupka, J., Jackeli, G. & Khaliullin, G. Kitaev-Heisenberg model on a honeycomb lattice: Possible exotic phases in iridium oxides A2IrO3 . Phys. Rev. Lett. 105, 027204 (2010).
Kotani, M. On the magnetic moment of complex ions (I). J. Phys. Soc. Jpn 4, 293–297 (1949).
Abragam, A. & Bleaney, B. Electron Paramagnetic Resonance of Transition Ions, 417–426 (Clarendon Press, 1970).
Mabbs, F. E. & Machin, D. J. Magnetism and Transition Metal Complexes, 68–84 (Chapman and Hall, 1973).
Cussen, E. J., Lynham, D. R. & Rogers, J. Magnetic order arising from structural distortion: Structure and magnetic properties of Ba2LnMoO6 . Chem. Mater. 18, 2855–2866 (2006).
Aharen, T. et al. Magnetic properties of the geometrically frustrated S=1/2 antiferromagnets La2LiMoO6 and Ba2YMoO6, with the B-site ordered double perovskite structure: Evidence for a collective spin-singlet ground state. Phys. Rev. B 81, 224409 (2010).
A de Vries, M., Mclaughlin, A. C. & Bos, J-W. G. Valence bond glass on an fcc lattice in the double perovskite Ba2YMoO6 . Phys. Rev. Lett. 104, 177202 (2010).
Carlo, J. P. et al. Triplet and in-gap magnetic states in the ground state of the quantum frustrated fcc antiferromagnet Ba2YMoO6 . Phys. Rev. B 84, 100404 (2011).
Qu, Z. et al. Spin-phonon coupling probed by infrared transmission spectroscopy in the double perovskite Ba2YMoO6 . J. Appl. Phys. 113, 17E137 (2013).
Stitzer, K. E., Smith, M. D. & zur Loye, H.-C. Crystal growth of Ba2MOsO6 (M=Li, Na) from reactive hydroxide fluxes. Solid State Sci. 4, 311–316 (2002).
Erickson, A. S. et al. Ferromagnetism in the Mott insulator Ba2NaOsO6 . Phys. Rev. Lett. 99, 016404 (2007).
Steele, A. J. et al. Low-moment magnetism in the double perovskites Ba2MOsO6 (M=Li,Na). Phys. Rev. B 84, 144416 (2011).
Stevens, K. W. H. On the magnetic properties of covalent XY6 complexes. Proc. R. Soc. Lond. A Math. Phys. Sci. 219, 542–555 (1953).
Chen, G., Pereira, R. & Balents, L. Exotic phases induced by strong spin-orbit coupling in ordered double perovskites. Phys. Rev. B 82, 174440 (2010).
Gangopadhyay, S. & Pickett, W. E. Spin-orbit coupling, strong correlation, and insulator-metal transitions: The J eff=3/2 ferromagnetic Dirac-Mott insulator Ba2NaOsO6 . Phys. Rev. B 91, 045133 (2015).
Helgaker, T., Jørgensen, P. & Olsen, J. Molecular Electronic-Structure Theory (Wiley, 2000).
Faughnan, B. W. Electron-paramagnetic-resonance spectrum of Mo5+ in SrTiO3—an example of the dynamic Jahn-Teller effect. Phys. Rev. B 5, 4925–4931 (1972).
Katukuri, V. M. et al. Electronic structure of low-dimensional 4d5 oxides: Interplay of ligand distortions, overall lattice anisotropy, and spin-orbit interactions. Inorg. Chem. 53, 4833–4839 (2014).
Wiebe, C. R. et al. Frustration-driven spin freezing in the S=1/2 fcc perovskite Sr2MgReO6 . Phys. Rev. B 68, 134410 (2003).
Mclaughlin, A. C. Simultaneous Jahn-Teller distortion and magnetic order in the double perovskite Ba2SmMoO6 . Phys. Rev. B 78, 132404 (2008).
Wallace, T. K., Colman, R. H. & Mclaughlin, A. C. A variable temperature synchrotron X-ray diffraction study of the ferroelastic double perovskite Ba2GdMoO6 . Phys. Chem. Chem. Phys. 15, 8672–8677 (2013).
Kahn, O. & Kettle, S. F. A. Vibronic coupling in cubic complexes. Mol. Phys. 29, 61–79 (1975).
Prosandeev, S. A., Waghmare, U., Levin, I. & Maslar, J. First-order Raman spectra of AB' 1/2B'' 1/2O3 double perovskites. Phys. Rev. B. 71, 214307 (2005).
Doll, K., Dolg, M., Fulde, P. & Stoll, H. Quantum chemical approach to cohesive properties of NiO. Phys. Rev. B 55, 10282–10288 (1997).
Yang, J. et al. Ab initio determination of the crystalline benzene lattice energy to sub-kilojoule/mole accuracy. Science 345, 640–643 (2014).
Hozoi, L. et al. Longer-range lattice anisotropy strongly competing with spin-orbit interactions in pyrochlore iridates. Phys. Rev. B 89, 115111 (2014).
Bogdanov, N. A. et al. Magnetic state of pyrochlore Cd2Os2O7 emerging from strong competition of ligand distortions and longer-range crystalline anisotropy. Phys. Rev. Lett. 110, 127206 (2013).
Werner, H. J., Knowles, P. J., Knizia, G., Manby, F. R. & Schütz, M. Molpro: a general-purpose quantum chemistry program package. Wiley Rev. Comp. Mol. Sci. 2, 242–253 (2012).
Peterson, K. A., Figgen, D., Dolg, M. & Stoll, H. Energy-consistent relativistic pseudopotentials and correlation consistent basis sets for the 4d elements Y-Pd. J. Chem. Phys. 126, 124101 (2007).
Figgen, D., Peterson, K. A., Dolg, M. & Stoll, H. Energy-consistent pseudopotentials and correlation consistent basis sets for the 5d elements Hf-Pt. J. Chem. Phys. 130, 164108 (2009).
Dunning, T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023 (1989).
Lim, I. S., Stoll, H. & Schwerdtfeger, P. Relativistic small-core energy-consistent pseudopotentials for the alkaline-earth elements from Ca to Ra. J. Chem. Phys. 124, 034107 (2006).
Fuentealba, P., Preuss, H., Stoll, H. & von Szentpály, L. A proper account of core-polarization with pseudopotentials: single valence-electron alkali compounds. Chem. Phys. Lett. 89, 418–422 (1982).
Fulde, P. Wavefunction-based electronic-structure calculations for solids. Nat. Phys 12, 106–107 (2016).
Fulde, P. Correlated Electrons in Quantum Matter (World Scientific, 2012).
Knowles, P. J. & Werner, H.-J. Internally contracted multiconfiguration-reference configuration interaction calculations for excited states. Theor. Chim. Acta 84, 95–103 (1992).
Werner, H.-J. & Knowles, P. J. An efficient internally contracted multiconfiguration-reference configuration interaction method. J. Chem. Phys. 89, 5803–5814 (1988).
Berning, A., Schweizer, M., Werner, H.-J., Knowles, P. J. & Palmieri, P. Spin-orbit matrix elements for internally contracted multireference configuration interaction wavefunctions. Mol. Phys. 98, 1823–1833 (2000).
Bolvin, H. An alternative approach to the g-matrix: Theory and applications. ChemPhysChem 7, 1575–1589 (2006).
Vancoillie, S., Malmqvist, P. & Pierloot, K. Calculation of EPR g tensors for transition-metal complexes based on multiconfigurational perturbation theory (CASPT2). ChemPhysChem 8, 1803–1815 (2007).
Acknowledgements
We thank V. Kataev for discussions. Part of the computations were carried out at the High Performance Computing Center (ZIH) of the Technical University Dresden. We acknowledge financial support from the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG)—SFB-1143 and HO-4427/2.
Author information
Authors and Affiliations
Contributions
L.X. carried out the ab initio quantum chemistry calculations, with assistance from N.A.B., A.P., P.F. and L.H. The mapping of the ab initio data onto the effective vibronic model was performed by L.X., L.H. and P.F. L.H., P.F. and J.vdB. designed the project. L.X. and L.H. wrote the paper, with contributions from all other coauthors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Xu, L., Bogdanov, N., Princep, A. et al. Covalency and vibronic couplings make a nonmagnetic j=3/2 ion magnetic. npj Quant Mater 1, 16029 (2016). https://doi.org/10.1038/npjquantmats.2016.29
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/npjquantmats.2016.29