Scalable randomised benchmarking of non-Clifford gates

Abstract

Randomised benchmarking is a widely used experimental technique to characterise the average error of quantum operations. Benchmarking procedures that scale to enable the characterisation of n-qubit circuits rely on efficient procedures for manipulating those circuits and, as such, have been limited to subgroups of the Clifford group. However, universal quantum computers require additional, non-Clifford gates to approximate arbitrary unitary transformations. We define a scalable randomised benchmarking procedure over n-qubit unitary matrices that correspond to protected non-Clifford gates for a class of stabiliser codes. We present efficient methods for representing and composing group elements, sampling them uniformly and synthesising corresponding poly(n)-sized circuits. The procedure provides experimental access to two independent parameters that together characterise the average gate fidelity of a group element.

Introduction

A key step to realising a large-scale universal quantum computer is demonstrating that decoherence and other realistic imperfections are small enough to be overcome by fault-tolerant quantum computing protocols.^1,2 Randomised benchmarking (RB)^3–6 has become a standard experimental technique for characterising the average error of quantum gates partly because of its insensitivity to state preparation and measurement errors. Benchmarking provides robust estimates of average gate fidelity^6,7 and it can characterise specific interleaved gate errors,^8,9 addressability errors¹⁰ and leakage errors.^11–13

RB techniques that efficiently scale to many qubits have been limited to subgroups of gates in the Clifford group, as computations with this group are tractable.⁶ However, the Clifford group is not enough for general quantum computations.¹⁴ Previous work generalises RB to groups that include non-Clifford gates,^15,16 but only on single qubits, a significant limitation. Methods for bounding the average fidelity of specific types of non-Clifford gates have also been considered.¹⁷

We present a scalable RB procedure that includes important non-Clifford circuits, such as circuits composed from $T=\sqrt[4]{Z}$ and controlled-NOT (CNOT) gates that naturally occur in fault-tolerant quantum computations. The n-qubit matrix groups we study are a generalisation of the standard dihedral group and coincide in some cases with protected gates in stabiliser codes, such as k-dimensional colour codes.¹⁸ Circuits built from these gates cannot be universal but do constitute significant portions of magic state distillation protocols,^19,20 repeat-until-success circuits²¹ and the vital quantum Fourier transform.²² We show that there are efficient methods for representing and composing group elements, sampling them uniformly and synthesising corresponding circuits whose size grows polynomially with the number of qubits n. The benchmarking procedure provides experimental access to two independent noise parameters through exponential decays of average sequence fidelities.

Results

The quantum circuits we consider are products of CNOT gates ${\mathrm{\Lambda }}_{12}\left(X\right)|u,v〉:=|u,u\oplus v〉$, bit-flip gates $X|u〉:=|u\oplus 1〉$ and single-qubit m-phase gates $Z_m|u〉:={\omega }_m^u|u〉$, where ${\omega }_m=e^{i2\pi /m}$. More concisely, the circuits of interest are given by the group

$$\begin{array}{}\text{(1)}& G_m:=〈{\mathrm{\Lambda }}_{ij}\left(X\right),X\left(j\right),Z_m\left(j\right)〉/〈{\omega }_m〉.\end{array}$$

We call this group a CNOT-dihedral group, as it is generated by CNOTs and a single-qubit dihedral group. Although we prove certain results for general m, we focus mainly on the case of m=2^k. This case affords efficient benchmarking and contains non-Clifford gates of interest, such as $T=\sqrt[4]{Z}$, controlled-$\sqrt{Z}$ (defined as ${\mathrm{\Lambda }}_{12}\left(\sqrt{Z}\right)|u,v〉:=i^{uv}|u,v〉$) and controlled–controlled–Z (defined as ${\mathrm{\Lambda }}_{123}\left(Z\right)|u,v,w〉:={\left(-1\right)}^{uvw}|u,v,w〉$), which is locally equivalent to a Toffoli gate.

Our interest in the dihedral group was motivated by symmetries of stabiliser codes. However, another group that may have similar properties is $G_{p,m}:=〈{\mathrm{\Lambda }}^{\left(p\right)}\left(X\right),X\left(j\right),Z_m\left(j\right)〉/〈{\omega }_m〉$ where Λ^(p)(X) is a p-controlled-NOT gate. Not all entangling gates are suitable for randomised benchmarking though. Our arguments imply that the group $〈{\mathrm{\Lambda }}_{ij}\left(Z\right),X\left(j\right),Z_m\left(j\right)〉$ does not yield an efficient benchmarking procedure, as twirling over this group produces a map with exponentially many parameters.

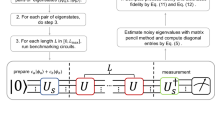
The benchmarking procedure we present here both generalises¹⁶ and extends naturally to interleaving gates to estimate individual gate fidelities.^8,9 The procedure closely follows¹⁰ but we describe it in some detail for completeness. Choose a sequence of ℓ+1 unitary gates in which the first ℓ gates are uniformly random elements $g_{j_1}$, $g_{j_2}$, …, $g_{j_{\ell }}$ of $G_{2^k}$ and the (ℓ+1)^st gate is $g_{{\mathbf{j}}_{\ell }}^{-1}:=g_{j_1}^{†}\dots g_{j_{\ell }}^{†}$ where j_ℓ denotes the ℓ-tuple (j₁, … j_ℓ) labelling the sequence. We show later that elements of $G_{2^k}$ can be efficiently sampled and $g_{{\mathbf{j}}_{\ell }}^{-1}$ can be efficiently computed. For each sequence, we prepare an input state ρ, apply $S_{{\mathbf{j}}_{\ell }}:=g_{{\mathbf{j}}_{\ell }}^{-1}{g}_{j_{\ell }}\dots g_{j_1}$ and measure an operator E.

Assuming each gate g_i has an associated error ${\mathcal{E}}_i\left(\rho \right)$, the sequence $S_{{\mathbf{j}}_{\ell }}$ is implemented as

$$\begin{array}{}\text{(2)}& {\tilde{S}}_{{\mathbf{j}}_{\ell }}:={\mathcal{E}}_{{\mathbf{j}}_{\ell }^{-1}}\circ g_{{\mathbf{j}}_{\ell }}^{-1}\circ \left({○}_{i=1}^{\ell }\left[{\mathcal{E}}_{j_i}\circ g_{j_i}\right]\right)\end{array}$$

$$\begin{array}{}\text{(3)}& ={\mathcal{E}}_{{\mathbf{j}}_{\ell }^{-1}}\circ \left({○}_{i=1}^{\ell }\left[{\tilde{g}}_{j_i}^{†}\circ {\mathcal{E}}_{j_i}\circ {\tilde{g}}_{j_i}\right]\right)\end{array}$$

where each ${\tilde{g}}_{j_i}\in G_{2^k}$. The overlap with E is $\mathrm{Tr}\left[E{\tilde{S}}_{{\mathbf{j}}_{\ell }}\left(\rho \right)\right]$. Averaging this overlap over K independent sequences of length ℓ gives an estimate of the average sequence fidelity $F_{seq}\left(\ell ,E,\rho \right):=\text{Tr}\left[E{\tilde{S}}_{\ell }\left(\rho \right)\right]$ where ${\tilde{S}}_{\ell }\left(\rho \right):=\frac{1}{K}{\sum }_{{\mathbf{j}}_{\ell }}{\tilde{S}}_{{\mathbf{j}}_{\ell }}\left(\rho \right)$ is the average quantum channel.

Defining $\mathcal{E}$ to be the average of errors ${\mathcal{E}}_{\mathit{i}}$ and assuming for all i that $\delta {\mathcal{E}}_i:={\mathcal{E}}_i-\mathcal{E}$ is small, the average quantum channel is

$$\begin{array}{}\text{(4)}& {\tilde{S}}_{\ell }\left(\rho \right)=\mathcal{E}\circ {\left[{\mathcal{E}}_{G_{2^k}}\right]}^{\circ \ell }+O\left(\delta \mathcal{E}\right)\end{array}$$

where ${\overline{\mathcal{E}}}_{G_{2^k}}$ is the $G_{2^k}$-twirl of (see Materials and Methods). The error operator $\mathcal{E}$ is attributed to measurement error and perturbs E to a new operator E′. We decompose the input state and this final measurement operator in the Pauli basis to give $\rho ={\sum }_P{x}_{P}P/2^n$ and $E\prime ={\sum }_P{e}_{P}P$. Neglecting the $O\left(\delta \mathcal{E}\right)$ term, the average sequence fidelity is

$$\begin{array}{}\text{(5)}& F_{seq}\left(\ell ,E,\rho \right)=\mathrm{Tr}\left[E\prime {\left({\overline{\mathcal{E}}}_{G_{2^k}}\right)}^{\circ \ell }\left(\rho \right)\right]=A_Z{\alpha }_Z^{\ell }+A_R{\alpha }_R^{\ell }+e_I\end{array}$$

where $A_Z={\sum }_{P\in \mathcal{Z}/\left\{I\right\}}{e}_P{x}_P$ and $A_R={\sum }_{P\in P/\mathcal{Z}}{e}_P{x}_P$.

To see this, it is convenient to express ${\overline{\mathcal{E}}}_{G_{2^k}}$ in a corresponding Liouville representation $R^{\overline{\mathcal{E}}}$ (see Methods). In this representation, $R^{\overline{\mathcal{E}}}$ is diagonal with three distinct diagonal elements corresponding to sets of Pauli operators: the identity I has value 1, the Z-type Pauli operators $\mathcal{Z}/\left\{I\right\}$ have value α_Z and the remaining Pauli operators $\mathcal{P}/\mathcal{Z}$ have value α_R. The Pauli operator P then contributes e_Px_Pα^ℓ to F_seq(ℓ, E, ρ), where α is one of 1, α_Z or α_R depending on P.

In a spirit similar to simultaneous RB,¹⁰ each of the two exponential decays ${\alpha }_Z^{\ell }$ and ${\alpha }_R^{\ell }$ can be observed by choosing appropriate input states. For example, if we choose the input state $|0\dots 0〉$, then $F_{\mathrm{seq}}=e_I+A_0{\alpha }_Z^{\ell }$ where $A_0={\sum }_{P\in \mathcal{Z}/\left\{I\right\}}{e}_P$. On the other hand, if we choose $|+\dots +〉:={\sum }_{b\in {\left\{0,1\right\}}^n}|b〉$, then $F_{seq}=e_I+A_{+}{\alpha }_R^{\ell }$ where $A_{+}={\sum }_{P\in \mathcal{X}/\left\{I\right\}}{e}_P$. State preparation errors may lead to deviation from a single exponential decay, but this is detectable. The channel parameters α_Z and α_R can be extracted by fitting the average sequence fidelity. The corresponding depolarising channel parameter is a weighted average $\alpha =\left({\alpha }_Z+2^n{\alpha }_R\right)/\left(2^n+1\right)$, and the average gate error is given by $r=\left(2^n-1\right)\left(1-\alpha \right)/2^n$ (see ref. 6).

The Materials and Methods section is devoted to proving the technical results that enable the benchmarking procedure such as a canonical decomposition of G_m, efficient computation within $G_{2^k}$ and twirling over $G_{2^k}$ to obtain the averaged quantum channel.

Discussion

Our results enable scalable benchmarking of a natural family of non-Clifford circuits related to quantum error-correcting codes. In principle, our procedure allows efficient benchmarking of isolated non-Clifford gates, as well as large sub-circuits for state distillation^19,20 or repeat-until-success protocols.²¹ These sub-circuits can be characterised with our procedure using physical gates or logical gates on protected qubits. Altogether with standard Clifford benchmarking, our procedures enable characterisation of the full range of gates used in the leading fault-tolerant quantum computing protocols. As multi-qubit benchmarking is well within experimental reach,^9,23,24 we expect an optimised implementation of our procedure to be quite practical.

Several natural questions arise from this work. First, one might address the asymptotically optimal cost of circuit synthesis for elements of the CNOT-dihedral groups, as well as the practical question of finding optimal circuit decompositions for elements of the smallest groups. We expect optimal circuits are computationally hard to find as n grows, but experimentally it is important to minimise the number of gates. Second, unlike the Clifford group, the CNOT-dihedral group is not a 2-design.⁵ It would be interesting to find a group (or set) containing a non-Clifford gate and that is a 2-design, and in which benchmarking can be done efficiently. Third, our results show that we can efficiently perform RB. However, we have not addressed the precise sense in which quantum computations over the CNOT-dihedral group can be efficiently simulated. This may be a subtle problem.^25,26 Last, there are generalised stabiliser formalisms, such as,²⁷ and it is natural to ask whether one of these describes how this group acts on some set of states.

Materials and methods

This section is devoted to proving the various results used in the benchmarking procedure: canonical decomposition of G_m, efficient computation in G_m and twirling over G_m, each of which is interesting in its own right. Let m be general and let us briefly set some notation. The matrix representation of G_m is set by identifying g∈G_m to the matrix that maps $|0^n〉:=|00\dots 0〉$ to $|b〉:=|b_1{b}_2\dots b_n〉$ with unit phase. We define the phase-flip gates $Z|u〉:={\left(-1\right)}^u|u〉$ and controlled-Z gates ${\mathrm{\Lambda }}_{12}\left(Z\right)|u,v〉:={\left(-1\right)}^{uv}|u,v〉$. The support of a bit string v∈{0, 1}ⁿ is $\mathrm{supp}\left(v\right)=\left\{j|v_j=1\right\}\subseteq \left[n\right]:=\left\{1,2,\dots ,n\right\}$. We refer to v and its support interchangeably, treating v as a set and vice versa. Let U be a single-qubit gate and U(v) denote the gate acting as U only on qubits in the support of v. Given J⊆[n] or elements i, j, … ∈[n], we also use the shorthand U(J) and U(i, j, …). $\mathcal{P}:=〈X\left(j\right),Z\left(j\right)〉/〈i〉$ denotes the n-qubit Pauli group and we define $\mathcal{X}:=〈X\left(j\right)|j\in \left[n\right]〉$, $\mathcal{Z}:=〈Z\left(j\right)|j\in \left[n\right]〉$, $c\mathcal{X}:=〈{\mathrm{\Lambda }}_{ij}\left(X\right)|i,j\in \left[n\right],i\ne j〉$ and $c\mathcal{Z}:=〈{\mathrm{\Lambda }}_{ij}\left(Z\right)|i,j\in \left[n\right],i<j〉$.

Canonical form of G_m

Our first goal will be to put G_m in a canonical form (the main result is contained in Theorem 1). The rewriting identities shown in Figure 1 allow us to commute diagonal elements of G_m through Λ_ij(X) and X(j) gates. The rules for bit-flip gates are a special case of the CNOT rules. The following Lemma follows directly from definitions and formalises the role of the rewriting identities in understanding the group’s structure.

Figure 1

Rewriting identities. Controlled-phase gate notation carrying the label a denotes a controlled-(Z_m)^a gate. (a) This is the only identity that increases the number of controls. (b) This identity preserves the number of controls.

Lemma 1: Let W_m denote the subgroup of diagonal matrices of G_m and let $\Pi =〈{\Lambda }_{ij}\left(X\right),X\left(j\right)〉$ denote the subgroup of permutation matrices. Then, G_m is isomorphic to a semi-direct product of groups G_m≃W_m⋊Π.

The proof of Lemma 1 is given in the Supplementary Material. Note that by definition $\Pi =\mathcal{X}⋊c\mathcal{X}$. As $\mathcal{X}\simeq {\mathbb{}}_2^n$ and $c\mathcal{X}\simeq {\mathrm{GL}}_n\left({\mathbb{}}_2\right)$, each element π∈Π can be associated with an n-bit string $c\in {\mathbb{}}_2^n$ and an n by n invertible 0–1 linear transformation $B\in {\mathrm{GL}}_n({\mathbb{}}_2)$ such that $\pi |b〉=|Bb\oplus c〉$. Here ${\mathbb{F}}_2$ denotes the field with two elements. Furthermore, $\left|\Pi \right|=2^n{\prod }_{\ell =0}^{n-1}\left(2^n-2^{\ell }\right)$.

It remains to better understand W_m (see Lemma 3 for the main result). Let D_m denote the group of 2ⁿ by 2ⁿ diagonal unitary matrices D with elements $〈b\left|D\right|b〉={\omega }_m^{f\left(b\right)}$. Here $f:{\mathbb{}}_2^n\to {\mathbb{Z}}_m$ is a function that assigns mth roots of unity to the diagonal and ${\mathbb{}}_m$ is the ring of integers modulo m. Since G_m is generated by permutation matrices and products of m-phase gates, W_m⊆D_m.

Let $ℛ\subset {\mathbb{Z}}_m\left[x_1,\dots ,x_n\right]$ denote the polynomial ring whose elements are $p\left(x\right):=p\left(x_1,\dots ,x_n\right)={\sum }_{\alpha \in {\left\{0,1\right\}}^n}{p}_{\alpha }{x}^{\alpha }$ where α=α₁ … α_n is a multi-index, $p_{\alpha }\in {\mathbb{}}_m$ and $x^{\alpha }=x_1^{{\alpha }_1}\dots x_n^{{\alpha }_n}$ is a monomial. The multi-index takes values in {0, 1}ⁿ as a convenient notation, as we will evaluate p(x) on binary strings, so $x_j^2=x_j$. The degree of a monomial is denoted $\left|\alpha \right|$. We mainly consider ℛ as an additive group. The next Lemma follows from the definition of group isomorphism and the fact that each function f(b) can be expressed as a polynomial in ℛ.

Lemma 2: Let p(b) denote evaluation of p on the n-bit binary string b=b₁ … b_n with operations in ${\mathbb{}}_m$. The function $\Phi :ℛ\to D_m$ given by $〈b\left|\Phi \left(p\right)\right|b〉={\omega }_m^{p\left(b\right)}$ is a group isomorphism.

The proof of Lemma 2 is given in the Supplementary Material. The rewriting identities give the action of Π on W_m by conjugation. Let ${\overline{W}}_m:=〈Z_m\left(j\right)〉$. On the basis of a similar application of the rewriting identities as in Lemma 1, $W_m=〈\pi {\overline{W}}_m{\pi }^{†}|\pi \in \Pi 〉$. As $W_m\subseteq D_m\simeq ℛ$, Φ⁻¹ associates a polynomial in ℛ to each element of W_m. By our chosen convention, matrices representing elements w∈W_m are given modulo a global phase factor $〈{\omega }_m〉$ such that $w|0^n〉=|0^n〉$. Therefore, the preimages Φ⁻¹(w) have zero constant term—i.e., p_α=0 when $\left|\alpha \right|=0$. Through Φ, the rewriting identities define an action of Π on ℛ that, respectively, takes x₁x₂ … x_px_j to

$$\begin{array}{}\text{(6)}& -2x_1{x}_2\dots x_p{x}_i{x}_j+x_1{x}_2\dots x_p{x}_i+x_1{x}_2\dots x_p{x}_j\end{array}$$

and x₁x₂…x_px_ix_j to

$$\begin{array}{}\text{(7)}& -x_1{x}_2\dots x_p{x}_i{x}_j+x_1{x}_2\dots x_p{x}_i.\end{array}$$

Equation (6) increments the degree of a monomial and multiplies its coefficient by −2, whereas Equation (7) does not change the degree. Another way to understand iterated applications of Equation (6) is to observe that

$$\begin{array}{}\text{(8)}& x_1\oplus x_2\oplus \dots \oplus x_N=\sum _{\alpha \in {\mathbb{Z}}_2^N,\left|\alpha \right|\ne 0}{\left(-2\right)}^{\left|\alpha \right|-1}{x}^{\alpha }.\end{array}$$

This fact relates how single qubit Z_m gates acting on mod 2 linear combinations of input bits are equivalent to products of certain controlled-phase gates.

There is an element of W_m corresponding to each monomial term of non-zero degree, and the coefficient of this term has the form $p_{\alpha }\in {\left(-2\right)}^{\left|\alpha \right|-1}{\mathbb{Z}}_m$, as we will now see (see Supplementary Materials for further details.). We choose a subset of qubits J, fix any j∈J and define a permutation gate and corresponding polynomial

$$\begin{array}{}\text{(9)}& {\pi }_{J,j}:=\prod _{\begin{array}{c}k\in J\\ k\ne j\end{array}}{\mathrm{\Lambda }}_{kj}\left(X\right);p_J\left(x\right):=\sum _{\begin{array}{c}\alpha \subseteq J\\ \left|\alpha \right|\ne 0\end{array}}{\left(-2\right)}^{\left|\alpha \right|-1}{x}^{\alpha }.\end{array}$$

By Equation (8), $\mathrm{\Phi }\left(p_J\right)={\pi }_{J,j}{Z}_m\left(j\right){\pi }_{J,j}^{†}\in W_m$; i.e., this circuit has a polynomial with one term of degree $\left|J\right|$. As Φ(Z_m(j))=x_j, scaled monomials of successive degrees |α| and with coefficients in ${\left(-2\right)}^{\left|\alpha \right|-1}{\mathbb{}}_m$ can be generated inductively by composing these circuits. Take all linear combinations of these over ${\mathbb{}}_m$ to find

Lemma 3: W_m is isomorphic to the subgroup $\mathcal{W}<ℛ$ given by

$$\begin{array}{}\text{(10)}& \left\{p\in ℛ|p_{\varnothing }=0\mathrm{and}\forall \alpha \ne \varnothing ,p_{\alpha }\in {\left(-2\right)}^{\left|\alpha \right|-1}{\mathbb{Z}}_m\right\}.\end{array}$$

We can now directly compute $\left|G_m\right|$.

Corollary 1

$$\begin{array}{}\text{(11)}& \left|G_m\right|=2^n\prod _{\ell =0}^{n-1}\left(2^n-2^{\ell }\right)\prod _{t=1}^n{\left(\frac{LCM\left(2^{t-1},m\right)}{2^{t-1}}\right)}^{\left(\begin{array}{c}n\\ t\end{array}\right)}.\end{array}$$

Proof: Let o_m(a)=LCM(a, m)/a denote the order of a in ${\mathbb{}}_m$. Observe that ${\left(-2\right)}^{\left|\alpha \right|-1}{\mathbb{}}_m\simeq {\mathbb{}}_{o_m\left(2^{\left|\alpha \right|-1}\right)}$ as additive groups. Therefore, W_m is isomorphic to a direct product of additive cyclic groups $A_m:={\prod }_{t=1}^n{\mathbb{}}_{o_m\left(2^{t-1}\right)}^{\left(\begin{array}{c}n\\ t\end{array}\right)}$. This shows that $\left|G_m\right|=\left|A_m\right|\left|\Pi \right|$.

Putting everything together, we have

Theorem 1: Any element of G_m can be written in canonical form as the composition of a sequence of phase gates (comprising an element of W_m whose form is given in Lemma 3), a sequence of CNOT gates and a sequence of bit-flip gates.

Efficient computation in $G_{2^k}$

Our next goal is to present efficient methods for computing with G_m. Suppose we fix value of m so that it is not a function of n. Any labelling of group elements will have length proportional to $s{=\log }_2\left|G_m\right|$. If m is odd, then ${\log }_2\left|G_m\right|=\left(2^n-1\right){\log }_{2}m{+\log }_2\left|\Pi \right|$, whereas if m=2^k then ${\log }_2\left|G_{2^k}\right|=\sum _{t=1}^k\left(k-t+1\right)\left(\begin{array}{c}n\\ t\end{array}\right){+\log }_2\left|\Pi \right|$. Therefore, s=Ω(2ⁿ) whenever m is odd (see Supplementary Materials for further details.), and in general we cannot efficiently represent elements of G_m as the number of qubits grows. However, s=O(n^k) for the special case m=2^k, and the story is different. We focus on this special case for the remainder of this article.

An element g∈G_m can be written as a product g=uvw where w∈W_m is a diagonal matrix, $v\in c\mathcal{X}$ is a CNOT circuit and $u\in \mathcal{X}$ is a tensor product of bit-flips. This transforms n-qubit quantum states as $g|b〉={\omega }_m^{p\left(b\right)}|Bb\oplus c〉$ where $p\in \mathcal{W}$, $B\in {\mathrm{GL}}_n\left({\mathbb{}}_2\right)$ and $c\in {\mathbb{}}_2^n$. Group elements are in bijective correspondence with the triples (p, B, c). The polynomial p has maximum degree k and at most $\sum _{t=0}^k(\begin{array}{c}n\\ t\end{array})=O\left(n^k\right)$ nonzero coefficients, each contained in ${\mathbb{}}_{2^k}$.

The product of group elements g₁, g₂∈G_m,

$$\begin{array}{}\text{(12)}& g_2{g}_1|b〉={\omega }_m^{p_1\left(b\right)+p_2\left(B_{1}b\oplus c_1\right)}|B_2{B}_{1}b\oplus B_2{c}_1\oplus c_2〉,\end{array}$$

is given by the triple

$$\begin{array}{}\text{(13)}& \left(p_1\left(x\right)+p_2\left(B_{1}x\oplus c_1\right),B_2{B}_1,B_2{c}_1\oplus c_2\right).\end{array}$$

The products B₂B₁ and B₂c₁⊕c₂ can be computed in O(n³) time, and polynomials in $\mathcal{W}$ can be added in O(n^k) ring operations. We need to show that p₂(B₁x⊕c₁) can also be computed efficiently.

Consider a triple (p, B, c) and let B_j denote the jth row of B and J_j=supp(B_j). Define x′=Bx⊕c. Then, for any j∈[n], using Equations (8) and (9),

$$\begin{array}{}\text{(14)}& x_j^{\prime }\left(x\right)=\left(\underset{\ell \in J_j}{\oplus }{x}_{\ell }\right)\oplus c_j=\{\begin{array}{ll}{p}_{J_j}\left(x\right)\hfill & \text{if}{c}_j=0\hfill \\ 1-p_{J_j}\left(x\right)\hfill & \text{if}{c}_j=1\hfill \end{array}\end{array}$$

has maximum degree k. When we substitute $x\prime =x_1^{\prime }\dots x_n^{\prime }$ into the degree k polynomial p(x), computations occur with coefficients in ${\mathbb{Z}}_{2^k}$. We compute each monomial (x′)^α with O(k) multivariate polynomial multiplications, each of which can be done term-by-term in O(n^2k+1) ring operations. We compute the term ${\left(-2\right)}^{\left|\alpha \right|-1}$ p_α(x′)^α with an additional O(n^k) ring operations to multiply each term of (x′)^α by a ${\left(-2\right)}^{\left|\alpha \right|-1}{p}_{\alpha }$ and accumulate the result. There are O(n^k) terms in p(x), so the total number of ring operations to compute p(x′) is O(n^3k+1). If c ≠ 0ⁿ, then it is possible that p(x′) has a non-zero constant term. With additional O(n^k) ring operations, p(x′) can be mapped to an equivalent polynomial in $\mathcal{W}$.

Uniformly sampling from G_2k is equivalent to uniformly and independently sampling from $\mathcal{W}$, $\mathrm{G}{L}_n\left({\mathbb{}}_2\right)$ and ${\mathbb{}}_2^n$. This can be done efficiently, as elements of $\mathcal{W}$ have maximum degree k; see also ref. 28 (see Supplementary Materials for further details.).

Given a triple (p, B, c), we synthesise a corresponding circuit from products of CNOT gates, bit-flip gates and single-qubit m-phase gates. Our goal is to efficiently synthesise a circuit whose size (number of gates) is polynomial in n but not to optimise this circuit. We independently synthesise circuits coinciding with p, B and c. As c corresponds to X(c), and a CNOT circuit for B can be found by Gaussian elimination,¹⁴ the new part of the algorithm synthesises a circuit for p.

We describe the circuit synthesis for p informally. The algorithm proceeds in k rounds. Begin by initialising a working polynomial q(x)←p(x), set a round counter t←k and set a quantum circuit U←I. Here ‘←’ denotes assignment. In round t, we synthesise a circuit corresponding to a polynomial p^(t)(x) that coincides with q(x) on its degree t terms. For each of the O(n^t) degree-t terms ${\left(-2\right)}^{\left|\alpha \right|-1}{p}_{\alpha }{x}^{\alpha }$ of q(x), we apply the constant-sized circuit $g_{\alpha }:={\pi }_{J,j}{\left(Z_{2^k}\left(j\right)\right)}^{p_{\alpha }}{\pi }_{J,j}^{†}$ setting U←g_αU, where J=supp(α) as in the proof of Lemma 3. The product of the g_α corresponds to $p^{\left(t\right)}\left(x\right):={\prod }_{\alpha \subseteq \left[n\right],\left|\alpha \right|=t}{p}_{\alpha }{p}_J\left(x\right)$. Therefore, we update q(x)←q(x)−p^(t)(x), which now has maximum degree t−1, decrement the round counter and proceed to the next round. The algorithm terminates when q(x)=0 and t=0. The total algorithm run-time and circuit size of the output U is O(n^k).

Twirling over $G_{2^k}$

A quantum channel is a completely positive trace-preserving map whose operator sum decomposition is $\mathcal{E}\left(\rho \right)={\sum }_k{A}_k\rho A_k^{†}$ where ${\sum }_k{A}_k^{†}{A}_k=I$. The twirl of $\mathcal{E}$ over a finite group G (G-twirl) is given by

$$\begin{array}{}\text{(15)}& {\overline{\mathcal{E}}}_G\left(\rho \right):=\frac{1}{\left|G\right|}\sum _{U\in G}{U}^{†}E\left(U\rho U^{†}\right)U.\end{array}$$

In what follows, we use several facts about group twirls. If G=AB is a direct product of groups, then ${\overline{\mathcal{E}}}_G\left(\rho \right)={\overline{\left({\overline{\mathcal{E}}}_A\right)}}_B\left(\rho \right)$, and if A is a normal subgroup of G (denoted $A⊲G$), then ${\overline{\mathcal{E}}}_G\left(\rho \right)={\overline{\left({\overline{\mathcal{E}}}_A\right)}}_{G/A}\left(\rho \right)$, where the twirl over the factor group G/A is over a set of coset representatives. Twirling any map over the Pauli group produces a Pauli channel.⁵ Consider a Pauli channel $\mathcal{E}\left(\rho \right)={\sum }_{Q\in \mathcal{P}}{\eta }_{Q}Q\rho Q$. Twirl this channel over any finite group G that has a permutation action on the set $\mathcal{P}$. The orbit of P∈$\mathcal{P}$ is $O_P:=\left\{V^{†}PV|V\in G\right\}$ and the stabiliser is $S_P:=\left\{V\in G|V^{†}PV=P\right\}$. The orbits define an equivalence relation P~Q if and only if O_P=O_Q. This relation partitions $\mathcal{P}$ into a disjoint union of orbits. By the orbit-stabiliser theorem and Lagrange’s theorem,²⁹ $\left|O_P\right|=\left|G/S_P\right|=\left|G\right|/\left|S_P\right|$. Therefore, the twirl, Equation (15), can be written

$$\begin{array}{}\text{(16)}& {\overline{\mathcal{E}}}_G\left(\rho \right)=\sum _{C\in \mathcal{C\backslash }}\sum _{P\in O_C}\left(\frac{{\sum }_{Q\in O_C}{\eta }_Q}{\left|O_C\right|}\right)P\rho P,\end{array}$$

where $\mathcal{C}$ is a set of representative elements, one from each orbit.

These facts allow us to compute the twirl over $G_{2^k}$ when k>1 by expressing it as a sequence of twirls. We begin by decomposing the group. Let ${\tilde{W}}_{2^k}:=W_{2^k}/\left({\overline{W}}_{2^k}\backslash \left\{I\right\}\right)$ and recall that ${\overline{W}}_{2^k}:=〈Z_{2^k}\left(j\right)〉$, then $W_{2^k}={\tilde{W}}_{2^k}{\overline{W}}_{2^k}$. As $c\mathcal{Z}⊲{\tilde{W}}_{2^k}$ and $\mathcal{Z}⊲{\overline{W}}_{2^k}$, we form the corresponding factor groups. Therefore, an element $w\in W_{2^k}$ can be written as $w=\tilde{w}\overline{w}={\tilde{w}}_1{\tilde{w}}_2{\overline{w}}_1{\overline{w}}_2$ where ${\tilde{w}}_1$ labels cosets ${\tilde{w}}_{1}c\mathcal{Z}$, ${\tilde{w}}_2\in c\mathcal{Z}$, ${\overline{w}}_1$ labels cosets ${\overline{w}}_1\mathcal{Z}$ and ${\overline{w}}_2\in \mathcal{Z}$. Finally, by Lemma 1, any element $g\in G_{2^k}$ factors as g=uvw where $u\in \mathcal{X}$, $v\in c\mathcal{X}$ and $w\in W_{2^k}$. Therefore, we have $g=u{\overline{w}}_2^{\prime }v{\tilde{w}}_2^{\prime }{\overline{w}}_1{\tilde{w}}_1$ where ${\overline{w}}_2^{\prime }=v{\overline{w}}_2{v}^{†}\in \mathcal{Z}$.

Our strategy is to use the decomposition to express the $G_{2^k}$-twirl as a sequential $\mathcal{P}$-twirl, c$\mathcal{X}$-twirl, c$\mathcal{Z}$-twirl, ${\overline{W}}_{2^k}/\mathcal{Z}$-twirl and ${\tilde{W}}_{2^k}/c\mathcal{Z}$-twirl. Each twirl can be computed in a straightforward manner using the facts we have described, and it reduces the number of independent parameters describing the channel until we have twirled over the whole of $G_{2^k}$ (see Supplementary Materials for further details.). The final twirled map is

$$\begin{array}{}\text{(17)}& \overline{\mathcal{E}}\left(\rho \right)={\beta }_I\rho +{\beta }_Z\sum _{P\in \mathcal{Z}/\left\{I\right\}}P\rho P+{\beta }_R\sum _{P\in P/\mathcal{Z}}P\rho P.\end{array}$$

In the Liouville representation in the Pauli basis, which has matrix elements $R_{PQ}^{\left(\overline{\mathcal{E}}\right)}=\text{Tr}\left(P\overline{\mathcal{E}}\left(Q\right)\right)/4^n$ where P and Q are n-qubit Pauli operators, this map has three diagonal blocks corresponding to I, $\mathcal{Z}/\left\{I\right\}$ and $\mathcal{P}/\mathcal{Z}$ with elements 1, α_Z:=1−4ⁿβ_R and α_R:=1−2ⁿβ_Z−(4ⁿ−2ⁿ)β_R, respectively.