Abstract
Ferroelectric tunnel junctions combine the phenomena of quantum-mechanical tunnelling and switchable spontaneous polarisation of a nanometre-thick ferroelectric film into novel device functionality. Switching the ferroelectric barrier polarisation direction produces a sizable change in resistance of the junction—a phenomenon known as the tunnelling electroresistance effect. From a fundamental perspective, ferroelectric tunnel junctions and their version with ferromagnetic electrodes, i.e., multiferroic tunnel junctions, are testbeds for studying the underlying mechanisms of tunnelling electroresistance as well as the interplay between electric and magnetic degrees of freedom and their effect on transport. From a practical perspective, ferroelectric tunnel junctions hold promise for disruptive device applications. In a very short time, they have traversed the path from basic model predictions to prototypes for novel non-volatile ferroelectric random access memories with non-destructive readout. This remarkable progress is to a large extent driven by a productive cycle of predictive modelling and innovative experimental effort. In this review article, we outline the development of the ferroelectric tunnel junction concept and the role of theoretical modelling in guiding experimental work. We discuss a wide range of physical phenomena that control the functional properties of ferroelectric tunnel junctions and summarise the state-of-the-art achievements in the field.
Similar content being viewed by others
Introduction
Electron tunnelling refers to the ability of electrons to traverse potential barriers exceeding their energy.1 This phenomenon is at the core of devices known as tunnel junctions, which consist of a nanometre-thick insulating layer separating two metallic electrodes. Significant interest in electron tunnelling has been triggered by the advent of spintronics—a branch of electronics using the electron spin in data storage and processing.2 The magnetic tunnel junction (MTJ) is the staple of spintronics.3 A MTJ exploits the switchable magnetisation of the two ferromagnetic (FM) metal electrodes. Changing their magnetic configuration from parallel to antiparallel, e.g., by an applied magnetic field, causes a large change in tunnelling resistance of the junction, an effect known as tunnelling magnetoresistance (TMR).4
In MTJs, the role of the barrier layer is passive: it separates the FM electrodes so that their magnetisations can be switched independently. Using the barrier layer as an active element of the device to control the charge and spin transport could be advantageous. This possibility is offered by complex oxide materials, which exhibit a wide range of properties, such as ferroelectricity, magnetoelectricity and metal–insulator transitions.5,6 These properties are exploited in ferroelectric and multiferroic tunnel junctions (MFTJs).7,8
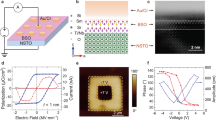
A ferroelectric tunnel junction (FTJ) consists of two metal electrodes separated by a nanometre-thick ferroelectric barrier layer, as illustrated in Figure 1a. The key feature of bulk ferroelectric materials is the spontaneous electric polarisation that can be switched between at least two stable orientations by applying an external electric field.9 In most cases, the ferroelectric crystal structure represents a small distortion of a high-symmetry paraelectric structure, as in the case of BaTiO3 (BTO), where the ferroelectric state corresponds to displacement of the Ti atom from the centrosymmetric position (Figure 1b). The perovskite oxides of the BTO family have a simple crystal structure that makes them relatively easy to grow. Moreover, as by symmetry all ferroelectrics are also piezoelectric and pyroelectric, these materials find widespread use in technological applications such as actuators and transducers. There are several other families of more complex ferroelectric oxides, which, however, have been less studied.9 Recently, organic ferroelectrics are also becoming mainstream.10
Schematic view of FTJ and the TER effect. (a) FTJ consisting of a nanometre-thick ferroelectric (FE) barrier between two metal (M) electrodes. (b) Crystal structure of the prototypical ferroelectric BaTiO3 showing the two polarisation states. (c, d) TER effect showing the correlation between switching of the polarisation of the ferroelectric in applied electric field (c) with the resistance of the FTJ (d). The low (high)-resistance states are indicated by red (blue) lines.
Although the FTJ concept was proposed long ago,11 it was contingent on the possibility to grow nanometre-thick ferroelectric films. Until recently, it was commonly accepted that there is a macroscopic critical thickness for ferroelectricity and that the ferroelectric polarisation would be suppressed by the depolarising field in nanometre-sized films.12,13 However, theoretical modelling14 and experimental work15–17 have demonstrated that when the ferroelectric is interfaced with a metal, the depolarising field is reduced due to screening of the polarisation charges and ferroelectricity can be maintained in nanometre-thick films. These developments paved the way for using ferroelectrics as barriers in tunnel junctions.
The signature property of the FTJ is that the reversal of the electric polarisation of the ferroelectric barrier in a FTJ produces a sizable change in resistance of the junction, as illustrated in Figures 1c and d. This phenomenon is known as the tunnelling electroresistance (TER) effect.18–20 FTJs are interesting from the point of view of device applications. Contrary to the ferroelectric capacitors, where leakage currents are detrimental to the device performance, the conductance of a FTJ is the functional characteristic of the device. This property allows using FTJs in non-volatile memory devices that are superior to the existing ferroelectric random access memories.21 An extension of the functionality of FTJ is achieved by making the electrodes FM, which makes it into a MFTJ.22 In a MFTJ, which can alternatively be thought of as a MTJ with a ferroelectric barrier, the TER and TMR effects coexist resulting in a four-state resistive device.23,24 In the past decade, we have witnessed marked progress in the elaboration of the properties of FTJs and MFTJs.25,26 This progress has been the result of a remarkable positive-feedback loop between theoretical modelling and experimental effort, during which theoretical predictions, based on both analytical and first-principles calculations, guided experimental effort, whereas experimental observations revealed novel phenomena stimulating theoretical work.
In this review, we outline this synergetic development with an emphasis on phenomena driven by the control of barrier polarisation in FTJs. In general, switching of the polarisation in the ferroelectric barrier affects the resistance of the FTJ in two principal ways: (i) modulation of the barrier height or (ii) modulation of the barrier width. All the mechanisms of TER that are discussed below fall in one of these two categories. The modulation of the barrier height typically results from asymmetry of the FTJ due to different electrode materials (section ‘Effects of electrostatic screening’), different atomic structure of the two interfaces (‘Effects of interface termination and interlayer’) and/or finite bias (‘Effects of finite bias’). In real materials, change in the barrier height is also associated with the complex band structure (CBS) modification (‘Effects of the electronic structure’). The modulation of the barrier width can be realised through the Schottky barrier at the interface and barrier metallisation (‘Effects of the Schottky barrier and barrier metallization’) or phase transitions at the interface (‘Effects of phase transitions at the interface’). We discuss all these mechanisms in some detail, providing links between theoretical modelling and experimental results where appropriate. In the section ‘Multiferroic tunnel junctions’, we briefly outline some results for FTJs with FM electrodes (i.e., MFTJs).
Mechanisms of TER and their experimental manifestation
Effects of electrostatic screening
In thin ferroelectric films, the interface polarisation charges are not completely screened by the adjacent metal electrodes and therefore the depolarising electric field E in the ferroelectric is not zero.27 The electrostatic potential associated with this field depends on the direction of the ferroelectric polarisation. If a FTJ is made of metal electrodes with different screening lengths, the asymmetry in the electrostatic potential profile alters an effective barrier height when the ferroelectric polarisation is reversed. This leads to the TER effect.7
Potential profile
Quantitatively, the magnitude and the shape of the electrostatic potential profile across the junction are determined by the polarisation P, the background dielectric permittivity εFE28 and the thickness d of the ferroelectric film, as well as the screening length λ of the electrodes. Within the Thomas–Fermi model, the ferroelectric polarisation charge at the interface is screened within the screening length (where ρ is the density of states at the Fermi energy and ε is the dielectric permittivity of the electrode), resulting in the exponential decay of the potential into the electrode.18 The magnitude of the electrostatic potential at the left (L) and right (R) interfaces is given by24
where εL,R are the electrode dielectric permittivities, γL,R=λL,R/εL,R is the normalised screening lengths and the positive (negative) sign corresponds to L (R) interfaces. For not too thick ferroelectric films, d~εFE(γL+γR), as in the case of FTJs, the potential profile depends on characteristics of the whole tunnel junction.
Figures 2a,b shows a representative electrostatic potential energy (eϕ) profile, calculated for two opposite polarisation directions in a FTJ with two different metals electrodes, one being a ‘good’ metal and the other a ‘bad’ metal.24 There is a notable difference in the magnitude of the electrostatic energy step at the interfaces, leading to a sign change in the average electrostatic potential across the barrier region when polarisation is reversed from right (→) to left (←). As a result, the average potential barrier height changes from U→=U0+e(ϕL+ϕR)/2 to U←=U0–e(ϕL+ϕR)/2. This is evident from Figures 2c,d showing the tunnelling potential energy profile for two opposite polarisation directions.
TER as a result of modulation of the tunnelling barrier height by ferroelectric polarisation switching. (a, b) Electrostatic potential energy profile across a FTJ for ferroelectric polarisation pointing right (a) and left (b) as shown on top panels by arrows. FTJ consists of two different metals (ML and MR, located at z<0 and z>d, respectively) separated by a ferroelectric tunnelling barrier (FE), which is located at 0<z<d (top panels). ϕL and ϕR denote potential steps at left and right interfaces, respectively. It is assumed that λL=0.07 nm, εL=ε0, λR=0.24 nm, εR=10 ε0, εFE=50 ε0 and P=40 μC/cm2. (c, d) Potential energy profiles across the FTJ for ferroelectric polarisation pointing right (c) and left (d). U→ and U← indicate average potential barrier heights for the two opposite polarisations. The dashed lines denote the Fermi energy EF. (e) Calculated TER as a function of barrier thickness d for different polarisation P of the ferroelectric barrier. It is assumed that d=1 nm, EF=2.0 eV and U0=2.0 eV. (f) Measured TER of highly strained BaTiO3 (BTO) films deposited on La0.7Sr0.3MnO3 electrodes versus BTO film thickness (tBTO) as obtained from conductive AFM measurements. After ref. 33 with permission.
Conductance and TER
This difference in the effective barrier height leads to a change in the tunnelling conductance, G. The measure of this change is the TER ratio, which we define here as TER=G←/G→ (same as the ON/OFF resistance ratio). At the most basic level, the tunnelling current through an asymmetric barrier can be described within the Wentzel–Kramers–Brillouin approximation, in which the exact form of the potential barrier is approximated by its average value.29,30 Within the Wentzel–Kramers–Brillouin approximation, TER can be written explicitly in terms of ferroelectric polarisation and screening lengths in the electrodes31,32
where m is the electron effective mass in the barrier and ΔU=U←−U→ is the barrier height change upon polarisation reversal (derived assuming ΔU≪U0). As seen from equation (2), TER is expected to depend stronger than exponentially on the barrier width d. For the parameters used in Figures 2a–d, we find ΔU≈0.4 eV and a steep increase of TER as a function of d (Figure 2e), resulting in TER~103 for a reasonable barrier width of ~2.5 nm and polarisation P=40 μC/cm2. Also from equation (2), TER depends exponentially on ferroelectric polarisation P, which dependence is also shown in Figure 2e. Therefore, the enhancement of polarisation magnitude and its stability is critical for observing a large TER in FTJs. The TER ratio increases with increasing ‘asymmetry’ of the electrodes as determined by γL/γR. In the limit γL/γR≫1, for not too large thickness (d≪εFEγL), the TER ratio approaches value of , which does not depend on electrode properties.
Experimentally, the TER effect was first observed with uncovered ferroelectric films, where local probe techniques were used to control the ferroelectric polarisation orientation and measure the tunnelling current through the film.31,33–35 In particular, it was demonstrated that highly strained BTO films retain robust room-temperature ferroelectricity down to 1 nm.33 A large resistance change was observed in these films correlated with ferroelectricity, as revealed from comparing images of ferroelectric domains and resistance maps of these domains. The resistance change between polarisation states was found to increase exponentially with BTO thickness, reaching 750 for 3-nm films at room temperature (Figure 2f). Fitting of the device I–V curves with the Brinkman model revealed a change of the average barrier height of the order of tenths of eV associated with polarisation reversal,31,34 which is consistent with the model predictions.
In addition, there have been several successful demonstrations of the TER effect using patterned ferroelectric films with top electrodes.36,37 In particular, tunnel junctions based on 2-nm-thick BTO films grown on La0.7Sr0.3MnO3 (LSMO) bottom electrodes with Au/Co top electrodes demonstrated robust ferroelectricity of BTO inside the junction.37 The remanent resistance of the device was shown to change hysteretically with ON/OFF ratios of ~100 and coercive fields matching ferroelectric switching. Fitting the I–V characteristics indicated that mechanisms based on the modulation of tunnel transmission through variation of the barrier height by ferroelectric polarisation are responsible for the TER effect.
Role of electrode work function
The model discussed above can be extended to include the possibility of different work functions of the two electrodes. In this case, different potential steps are expected at the two interfaces producing an electric field in the barrier even in the absence of ferroelectric polarisation. This field is screened by interface charges that are formed to balance the electrochemical potentials in the electrodes, as required by the short-circuit boundary condition, resulting in a change in the effective tunnelling barrier height from U0 to
where ΔW=WL−WR is the difference of the work functions of the left and right electrodes. It is seen that the effective barrier height can increase or decrease depending on sign of ΔW, which is expected to affect TER according to equation (2).
Experimentally, different potential steps at the two interfaces have been measured in Cr/BTO/Pt FTJs by reconstructing the electrostatic potential profile by hard X-ray photoemission spectroscopy.38 The effect of electrode’s work function on TER was explored for M/BiFeO3/Ca0.96Ce0.04MnO3 FTJs with different top metal electrodes (M=W, Co, Ni and Ir).39 Fitting of the I–V characteristics indicated that the M/FE interfacial barrier height increases with the electrode work function. This led to an increased resistance in the OFF state and a larger ON/OFF ratio for top electrodes with a larger work function. The results, however, also indicated that the higher TER comes at the cost of deteriorated switching characteristics. A large difference in TER was also observed for M/BTO/LSMO (M=Au and Cu) FTJs.40
Effects of the Schottky barrier and barrier metallisation
Another approach to produce a sizable TER effect is to modulate the barrier width by switching ferroelectric polarisation in a FTJ. This may be achieved by a reversible depletion/accumulation of charge in an interfacial region of a semiconducting electrode (modulation of the Schottky barrier) and/or reversible metallisation of an interfacial region in the barrier itself.
Schottky barrier
In a FTJ with a semiconducting electrode, which is characterised by a small Fermi energy and large screening length, the barrier width can be controlled by ferroelectric polarisation through the Schottky barrier. For example, if one of the electrodes in a FTJ is an n-type semiconductor and ferroelectric polarisation is pointing away from the semiconductor, electron carriers are depleted in the semiconductor adding a Schottky barrier to the ferroelectric tunnel barrier (Figure 3b). On the other hand, when the polarisation is pointing towards the semiconductor, electron carriers are accumulated which only leads to a local increase of the chemical potential, but does not change the barrier width in the FTJ (Figure 3a).
TER as a result of modulation of the tunnelling barrier width by ferroelectric polarisation switching. (a, b) Calculated potential energy profiles for ferroelectric polarisation pointing right (a) and left (b) as shown on top panels by arrows. FTJ consists of a metal electrode (M, located at z<0) and a semiconducting electrode (SC, located at z>d), separated by a ferroelectric tunnelling barrier (FE), which is placed at 0<z<d (top panels). The dashed lines denote the Fermi energy EF. d→ and d← indicate the average potential barrier width for the two opposite polarisations. It is assumed that λM=0.07 nm, εM=ε0, d=1 nm, n=3.4×1010 e/cm3, εSC=10 ε0, εFE=50 ε0 and P=40 μC/cm2. (c) Calculated TER as a function of carrier concentration n in the semiconducting electrode for different polarisation P of the ferroelectric barrier. TER is defined as G→/G←. It is assumed that d=1 nm, EF=2 eV and U=2 eV. (d) Energy profile of the conduction band minimum (CMB) in SrRuO3/BaTiO3/n-SrTiO3 tunnel junctions for two polarisation orientations (indicated by arrows) and doping concentration n=0.09 e/f.u. calculated using a model (solid lines) and first-principles (dots) approach. After ref. 43. (e) ON/OFF ratio as a function of Nb doping concentration in Pt/BaTiO3/Nb:SrTiO3 FTJs. After ref. 44 with permission. (f) Average resistance of Pt/BaTiO3/La0.7 Sr0.3MnO3 (Pt/BTO/LSMO) tunnel junctions as a function of BTO barrier thickness. The top-left inset shows the barrier for ON and OFF states as deduced from the fits of the I–V curves. The top inset shows the relative orientation of the BTO polarisation (arrow) in the ON and OFF states. After ref. 46 with permission.
Model calculations of the conductance of a metal/ferroelectric/semiconductor tunnel junction show very large TER ratio due to modulation of the Schottky barrier. Figure 3c shows the calculated TER ratio as a function of electron concentration n in a semiconducting electrode. Here the electronic potential profile (Figures 3a,b) is obtained by solving self-consistently the Poisson equation for the junction, imposing the boundary conditions at interfaces and assuming that the local electron concentration is a linear function of the electrostatic potential.41,42 As is seen from Figure 3c, the TER increases markedly when the carrier concentration is reduced. This reflects the increase of the Schottky barrier width for polarisation pointing into the semiconductor, as the result of the enhanced depletion region. The effect also increases with the polarisation due to a stronger electron depletion required to screen a larger polarisation charge. At a very high carrier concentration, n⩾1021 e/cm3, a metallic regime is reached, which corresponds to the case where the change in the barrier height controls the TER (‘Effects of electrostatic screening’).
This result is corroborated by density functional theory (DFT) calculations for a SrRuO3/BTO/n-SrTiO3 FTJ, where n-doped SrTiO3 (STO) serves as a semiconducting electrode.43 When the polarisation is pointing away from n-STO, electron depletion and the associated band bending near the interface lead to an additional narrow barrier formed within the n-STO electrode (Figure 3d, blue curve and symbols). When the polarisation is pointing into n-STO, however, the Schottky barrier is eliminated by electron accumulation (Figure 3d, red curve and symbols). Moreover, a conducting region within the BTO is formed near the interface, further reducing the tunnelling barrier width (the effect of barrier metallisation is discussed in the subsection ‘Barrier metallization’).
This physical mechanism for the enhanced TER explains the experimental data on Pt/BTO/Nb:STO FTJs, exhibiting resistance change as high as 104 at room temperature.44 In these FTJs, Nb-doped STO single-crystal substrates with Nb varying from 0.1 to 1% were used as n-doped semiconducting electrodes. The large TER was interpreted by the depletion or accumulation of carriers in Nb:STO depending on polarisation orientation of the barrier. This mechanism was found to be consistent with the measured TER dependence on the dopant concentration: the lower Nb concentration led to the higher Schottky barrier and hence the larger TER (Figure 3e). Interesting results were obtained for Pt/La1−xSrxMnO3/BTO/Nb:STO FTJs, where Sr doping was used to tune the chemical potential of the manganite to optimise the TER effect, and surprisingly high TER ratios (∼400%) were observed at room temperature for FTJs with BTO layer thickness down to 2 u.c.45
Barrier metallisation
In addition to the Schottky barrier in a semiconducting electrode, a metallic region within the ferroelectric barrier layer near interface may be formed, reducing the tunnelling barrier width in the ON state. The partial metallisation of the BTO barrier is seen in Figure 3d for polarisation pointing into the n-STO, where electrons are spilled from n-STO to BTO, due to their close electron affinities (3.9 and 4.0 eV, respectively). The effect of barrier metallisation was put forward to explain very large ON/OFF resistance ratios observed in Pt/BTO/LSMO46 and Co/PbTiO3 (PTO)/LSMO47 tunnel junctions. In particular, ON/OFF ratios up to 300 were observed in Pt/BTO/LSMO tunnel junctions at room temperature.46 On the basis of the measured capacitance change with reversal of ferroelectric polarisation of BTO, it was argued that there is an n-type semiconducting region at the BTO/LSMO interface. Upon biasing, the n-type region is driven to accumulation or depletion regimes with subsequent changes of the effective barrier width for tunnelling transport across the junction (Figure 3f). The measurement also indicated an exponential dependence of the resistance and TER on the BTO barrier width consistent with the expectation (Figure 3f). Similarly, it was found that the TER effect in a Co/PTO/LSMO tunnel junction is controlled by the change in the tunnelling barrier thickness upon reversal of polarisation of the ferroelectric PTO layer.47 On the basis of first-principles calculations, it was argued that the ferroelectric layer exhibits a reversible metallisation at one of the interfaces.
Effects of the electronic structure
Simple, free-electron models have been essential for understanding the basic physics of FTJs and the TER effect. At the same time, they have limitations, both in the depth of the description as well as in the range of the physical mechanisms that are captured. For example, the electrostatic profile in these models is determined by the screening length in the electrodes and the polarisation in the barrier, however, both of these are taken as parameters. Using first-principles DFT-based methods makes it possible to calculate self-consistently the distribution of the screening charge accounting for the density of states of the materials.48 DFT calculations also give the electrostatic potential corresponding to the charge distribution, which goes beyond the Tomas–Fermi approximation used in the model calculations, and accounts for the realistic electronic structure of the materials, as well as for details of the atomic structure of the interfaces. The work functions of the electrodes are also parameters in the model; however, they are routinely calculated for different surface terminations using first-principles calculations, as the difference between the Fermi energy of the material and the vacuum energy.49 The very existence of polarisation in ultrathin films cannot be predicted within simple models, but it is captured by first-principles calculations.14 These calculations also capture changes in the polarisation profile in the barrier due to interface boundary conditions,23 and take into account not only the electronic but also the ionic screening of the polarisation charge.50,51 Furthermore, first-principles calculations capture details of the bonding and the atomic structure of the interface,20 in particular the effect of different interface terminations and/or oxidation.52,53 Finally, first-principles calculations account for the details of the electronic structure of the electrode and barrier materials, involving multiple bands whose orbital character and symmetry matching across the interface largely determine the transmission coefficient.
An important effect of the electronic structure is that in complex insulators, such as STO and BTO, there is more than one evanescent state available for carriers in the bandgap.20,54 These states have different decay rates and hence contribute differently to the tunnelling current. The CBS of the insulator determines the rate of decay of the carriers in the bandgap. Formally, CBS is an analytical continuation of the real band structure into the complex momentum space, which reveals both the propagating and evanescent states supported by the material.55,56 The importance of the CBS and evanescent states was recognised as a powerful tool to analyse spin-transport properties of MTJs.54,57,58
In the case of ferroelectrics, the CBS has been calculated for BTO20,23,52,59 and PTO.60–63 The results show that there are multiple decay rates in the barrier for propagating states with different symmetry. The largest contribution to the transmission is expected from the bands that have lowest decay rates. For example, in the case of BTO, there are two evanescent states of Δ1 and Δ5 symmetry with the lowest decay rates in the bandgap (Figure 4a). For not too thick barriers, contributions to the tunnelling transmission are expected from both bands, provided that states compatible with these symmetries are available in the electrodes. It was also found that the bandgap and, respectively, the decay rates increase with the magnitude of the polarisation.20,52 For example, comparing the decay rates for paraelectric and ferroelectric BTO (Figure 4a) shows that the structural change driven by spontaneous polarisation increases the bandgap and enhances the decay rates of both the Δ1 and Δ5 bands.
Complex band structure and conductance in the BaTiO3-based FTJs. (a) Complex band structure of BaTiO3 in paraelectric (PE) and ferroelectric (FE) states. The two lowest decay rates of the evanescent states of Δ1 and Δ5 symmetry are displayed. After ref. 20 with permission. (b) The lowest decay rate as a function of k||=(kx, ky) in the two-dimensional Brillouin zone calculated at the Fermi energy, which is indicated in a by a vertical line. After ref. 20 with permission. (c) Calculated transmission as a function of k|| for a non-magnetic SrRuO3/BaTiO3/SrRuO3 FTJ with asymmetric interfaces for polarisation pointing toward the RuO2/BaO interface (left panel) and the TiO2/BaO interface (right panel).
The CBS is useful to make qualitative conclusions about mechanisms of tunnelling conductance; however, as a bulk property of the barrier, it is only a part of the device description. Direct first-principles transport computations are required for a full quantitative analysis of the conductance and TER. These are performed using the Landauer formula,64 which relates the conductance to the transmission probability between different propagating states in the electrodes
Here Tσ(k||) is the transmission probability of the electron with spin σ at the Fermi energy and k||=(kx, ky) is the Bloch wave vector corresponding to the periodicity in the plane of the junction. The transmission probability is calculated either using the Green’s function method65 or the wave-function matching method66,67 implemented in the context of DFT calculations. In both cases, the barrier with the interfaces is considered as a scattering region, connected to semi-infinite electrodes. The propagating states in one of the electrodes are scattered and transmitted into propagating states in the other electrode. Within the Green’s function method, the transmission probability is expressed through the Green’s function of the scattering region connected to the electrodes, G, as68
where ΓL (ΓR) are the escape rates to the left (right) electrodes, which are calculated form the surface Green’s function of the electrodes.69 The trace is over all the orbital indices. Within wave-function matching method, the wave function in the electrodes is written as an incoming and reflected wave on the left and a transmitted wave to the right67
where the scattering region is situated 0<z<d, and rij and tij are the reflection and transmission amplitudes between the Bloch states, respectively. By matching the electrode wave function with that of the scattering region at both interfaces (z=0 and z=d), the transmission coefficients are obtained, and the transition probability is given as where is the transmission amplitude normalised to unit flux.
An example of such full transport calculation is illustrated in Figure 4c, where the k||-resolved transmission in the two-dimensional Brillouin zone is plotted for a non-magnetic SrRuO3/BTO/SrRuO3 (SRO) FTJ for two polarisation directions. The transmission pattern seen for both polarisation states is determined by the CBS of the barrier, as follows from Figure 4b showing the k||-resolved lowest decay rate at the Fermi energy. It is evident from Figure 4c that, although features in the transmission distribution look similar for the two polarisation states, there is a notable difference in the overall contrast, indicating a sizable reduction in the total conductance and thus a large TER effect when polarisation is switched from pointing towards the RuO2/BaO interface to the TiO2/BaO interface (see section ‘Interface termination’ for further details). Full transport calculations have been carried out for FTJs featuring the perovskite ferroelectrics BTO20,23,59 and PTO,63 as well as organic ferroelectric barriers.53,70
Effects of interface termination and interlayer
Interface termination
The requirement of two different electrodes is not mandatory for observing TER in FTJs. Symmetry can be broken by different terminations at the two interfaces of the junction. For example, in FTJs with two SRO electrodes and BTO barrier, epitaxial unit cell by unit cell growth of the perovskite heterostructure preserves the AO–BO2 (A=Sr, Ba; B=Ru, Ti) sequence of the atomic layers, resulting in SrO/TiO2 termination at the left interface and BaO/RuO2 at the right interface of the FTJ (Figure 5a, top). The asymmetric interfaces lead to a different polarisation profile when the ferroelectric is switched. As seen from Figure 5a, when polarisation is pointing to the left, polar displacements between metal (M) and oxygen (O) ions in BTO are larger than those when polarisation is pointing to right. This sizable change in the polarisation magnitude affects the decay rate of the states carrying tunnelling current (in this case, Δ1 and Δ5 symmetry states shown in Figure 4a), resulting in a large TER effect (Figure 4c).23
Atomic structure, polarisation stability and TER in SrRuO3/BaTiO3/SrRuO3 FTJs. (a) Atomic structure of SRO/BTO(6 u.c.)/SRO FTJ. Displacements of the Ru and Ti cations are measured with respect to the O atoms in the same atomic plane. Red (blue) symbols correspond to polarisation of BaTiO3 pointing to the right (left). Open symbols correspond to Ba–O and Sr–O displacements; closed symbols correspond to Ti–O2 and Ru–O2 displacements. After ref. 23. (b) Same as a for SRO/BTO(6 u.c.)/STO/SRO FTJ with a 2-u.c. STO layer at the interface. After ref. 73 with permission. (c) Total energy per Ti atom as a function of polarisation of the 5-u.c.-thick BaTiO3 layer in SRO/BTO/SRO (dashed line) and SRO/BTO/STO/SRO (solid line) FTJs. After ref. 73. (d) Remanent P–V hysteresis loops in FTJs with no STO layer, STO inserted at the RuO2/BaO interface and the TiO2/BaO interfaces. After ref. 73 with permission.
It is well known that the interface atomic relaxations impose boundary conditions on polarisation, affecting ferroelectric stability in thin films.14,50 Asymmetric interfaces may produce a strong poling effect making one of the polarisation states preferential.71 In the case of SRO/BTO/SRO FTJs, the built-in dipole at the BaO/RuO2 interface (seen in Figure 5a from the Ru–O displacement at this interface) suppresses the polarisation when it is pointed towards this interface and for sufficiently thin BTO films leads to non-switchable polarisation.23,72,73 The calculated total energy as a function of polarisation (Figure 5c, dashed line) displays an asymmetric double-well potential with one of the minima being very shallow due to the built-in interface dipole. Interestingly, inserting a thin layer of STO at the BaO/RuO2-terminated interface counteracts this unfavourable interface dipole effect (Figure 5b). Both theory72 and experiment73 demonstrate that the associated change of the interface termination sequence to SrO/TiO2 on both sides of the heterostructure leads to a restoration of bi-stability with a smaller critical thickness, along with enhancement of the barrier for polarisation reversal (Figure 5c, solid line). The effect is evident from Figure 5d showing the increase of the remanent polarisation of the FTJ when the BaO/RuO2 interface is eliminated.73
Recently, it was demonstrated that the surface termination of the ferroelectric barrier layer in contact with a simple-metal electrode critically affects electroresistive properties.74 Using Co/BTO/LSMO, FTJs with either TiO2- or BaO-terminated BTO led to the opposite sign of TER. The TER ratio was found to be dependent on the fraction of the BaO termination at the interface, which was explained in terms of the termination-dependent depolarising field.50
Interface interlayer
At the same time, inserting a thin layer of dielectric at one of the interfaces in a FTJ provides asymmetry necessary for TER. Model calculations predict that TER is strongly enhanced due to the presence of the dielectric layer.75 The effect originates from the electrostatic potential in the dielectric being shifted up or down when the ferroelectric polarisation is switched. This changes substantially the tunnelling barrier height in the dielectric portion of the barrier (Figure 6a) resulting in a strong enhancement of TER. In the limit of perfect identical electrodes (λL, λR→0), we obtain within the Wentzel–Kramers–Brillouin approximation31
where dFE (dD) and εFE (εD) are thickness and the electric permittivity of the ferroelectric (dielectric) layer, and U is the average height of the composite barrier when P=0. It is seen from equation (7) that for small dD TER increases exponentially, which is in agreement with the more rigorous calculation shown in Figure 6b.75 These conclusions are consistent with the results of first-principles calculations showing that the inclusion of the STO interlayer at the BTO/SRO interface leads to the ferroelectric modulation of the electrostatic potential in the STO interlayer (Figure 6c).76 This enhances the TER, whose magnitude is scaled with STO thickness.
FTJs with a dielectric layer at one of the interfaces. (a) Geometry of a FTJ with inserted dielectric layer (D) and calculated potential energy profile for the two opposite polarisation orientations. The dielectric layer is described by the dielectric constant εD=10, potential barrier height UD=2.5 eV and thickness dD=0.5 nm. Other parameters are as follows: λ=0.1 nm, dFE=2.5 nm and P=20 μC/cm2. The Fermi energy (EF) is indicated by the dashed line. (b) Calculated TER as a function of thickness of the dielectric interlayer dD for two values of polarisation. Other parameters are the same as in a. (c) Electrostatic potential energy profile across SRO/BTO(6 u.c.)/STO(2 u.c.)/SRO FTJ calculated from first-principles for two polarisation orientations indicated by arrows. After ref. 76. The potential is averaged over the plane parallel to the interfaces. (d) Schematic of a FTJ with the top graphene electrode and the interfacial ammonia (NH3) layer for ferroelectric polarisation of BaTiO3 pointing up (bottom) and down (top). Courtesy of Alexey Lipatov.
Experimentally, the enhancement of TER is evident in FTJs with uncovered ferroelectric layers. Comparison of the TER results for FTJs with open and capped ferroelectric layers shows that the capped structures exhibit much more modest values of TER. This difference may be attributed to the presence of an additional dielectric layer between the local probe tip and the ferroelectric.31,33,34 Surface chemistry also has an essential role in these and related films, and likely affects the observed switching phenomena.77,78
We also note that the presence of the dielectric layer at the interface strongly affects the ferroelectric polarisation stability and therefore special attention needs to be given to this issue. Clear evidence of the effect of the interfacial layer has been demonstrated recently for FTJs with graphene electrodes.79 It was found that ferroelectric polarisation stability and resistive switching are strongly affected by a molecular layer at the graphene/BTO interface. For FTJs with an interfacial H2O layer, only one polarisation state was stable and the TER effect was impossible to observe. In contrast, for FTJs with an interfacial NH3 layer (Figure 6d), the polarisation was stable and switchable, and an enhanced TER effect reaching a magnitude of 6×103 was observed.
Effects of phase transitions at the interface
Using complex oxide materials, such as manganites La1−xAxMnO3 (A=Ca, Sr or Ba), as electrodes or interlayers in FTJs brings into play new interesting phenomena involving the coupling between ferroelectricity of the barrier and magnetism of the manganite. Strongly correlated manganite materials display a rich phase diagram that consists of competing phases with different conducting properties and magnetic orderings (Figure 7a).80 Normally, the control of different phases is achieved though chemical doping. Instead, a ferroelectric/manganite interface can be employed for electrostatic doping of the manganite with the advantage of being switchable by an applied electric field. The electrostatic doping occurs at such an interface due to polarisation charge on the ferroelectric side of the interface being screened by a build-up of opposite charge on the manganite side, effectively altering the hole concentration of the manganite near the interface. If the manganite has chemical composition x close to a phase boundary the reversal of polarisation can induce a magnetic (and/or metal–insulator) phase transition locally near the interface (red arrows in Figure 7a). For example, a FM to antiferromagnetic (AFM) phase transition was predicted theoretically for the La0.5Ba0.5MnO3/BTO interface.81 Because of a finite screening length in the manganite, the predicted magnetoelectric effect is confined within 2 u.c. near the interface (Figure 7b). Experimentally, the related effects have been observed in La0.8Sr0.2MnO3/PbZr0.2Ti0.8O3 (PZT) heterostructures.82,83
Polarisation controlled interfacial phase transitions. (a) Phase diagram showing the diversity of electronic and magnetic phases in bulk La1-xSrxMnO3. PM–I, PM–M, FM–I, FM–M, AFM–M and C–I denote paramagnetic insulator, paramagnetic metal, ferromagnetic insulator, ferromagnetic metal, antiferromagnetic metal and spin-canted insulator states, respectively. Red arrows show phase transitions that may be exploited in FTJs. After ref. 80. (b) Predicted FM–AFM phase transition at the interface between BTO and La0.5Sr0.5MnO3 induced by ferroelectric polarisation reversal in BTO. After ref. 81 Horizontal arrows indicate the orientation of ferroelectric polarisation; vertical arrows show magnetic moments on Mn atoms. (c) Change in the tunnelling current across a PZT(10 nm)/La1−xSrxMnO3 (5 nm) bilayer at various phase boundaries of LSMO: x=0.2 (left), x=0.33 (middle) and x=0.5 (right), measured by conductive AFM at room temperature. After ref. 87 with permission. (d) A schematic diagram of the LSMO/BTO/LCMO/LSMO FTJ with a thin layer (~1 nm) of La0.5Sr0.5MnO3 (LCMO) inserted at the interface. Reversal of ferroelectric polarisation leads to hole charge depletion or accumulation in the LCMO layer resulting in its phase transition from FM metal to AFM insulator, respectively. After ref. 86 with permission. (e) Resistance (R) as a function of pulsed poling voltage (Vpulse) measured at 40 K for junction with (J1, TER~100) and without (J2, TER~1.3) LCMO interlayer. The arrows indicate the direction of pulse sequence. After ref. 86 with permission. (f) Resistance (R) as a function of magnetic field (H) for a junction with the LCMO interlayer in the high- (top) and low- (bottom) resistance states. After ref. 86 with permission.
The electrically induced FM to AFM phase transition at the interface has important implications for FTJs. The FM metal phase in LSMO is half metallic with electronic density of states only in the majority spin channel.84 Switching the magnetic order near the interface from FM to A-type AFM order blocks the majority spin conduction due to the spin valve effect. As the spin polarisation is nearly 100% this ‘spin valve’ exhibits a huge difference in conductance between parallel and antiparallel configurations, giving rise to the large TER effect. First-principles calculations for a junction consisting of BTO as a barrier with La0.7Sr0.3MnO3 and La0.6Sr0.4MnO3 as the left and right electrodes, predicts a factor of 18 change of conductance with polarisation reversal due to the interface magnetic phase transition.85
These findings were confirmed in experiments on LSMO/BTO/LCMO/LSMO FTJs with a thin layer of La0.5Ca0.5MnO (LCMO) inserted at one of the interfaces.86 The doping of the LCMO (x=0.5) was intentionally chosen at the boundary between FM-metallic (x<0.5) and AFM-insulating (x>0.5) states. Reversal of ferroelectric polarisation was expected to produce hole charge depletion or accumulation in the LCMO layer resulting in a phase transition in the LCMO from FM metal to AFM insulator, respectively (Figure 7d). Indeed, it was found that ferroelectric polarisation switching caused the material to undergo the metal–insulator transition effectively changing the barrier width by converting part of the electrode into a barrier. This was accompanied by a giant TER ratio of about 100 measured at T=40 K (Figure 7, top panel). For reference, LSMO/BTO/LSMO junctions without the LCMO spacer layer demonstrated a low TER ratio of just about 1.3 (Figure 7, bottom panel).
Interfacial phase transitions were also investigated experimentally using PZT/La1−xSrxMnO3 bilayers with a conductive-AFM tip as a top electrode.87 A sign change of the TER was observed when the LSMO electrode composition was altered from x=0.2 to 0.5 (Figure 7c). This result is consistent with the phase diagram of LSMO (Figure 7a), suggesting that at x=0.2 hole accumulation (polarisation points away from LSMO) leads to the FM insulator to FM metal phase transition, whereas at x=0.5 it leads to the FM metal to AFM insulator phase transition.
Effects of finite bias
The majority of theoretical effort has been directed towards elaborating the TER effect at zero bias, in which case structural asymmetry is necessary to break the degeneracy between the two polarisation directions. At the same time, applied bias is a simple and dynamically tunable way to create asymmetry in the junction. Within simple models, TER was calculated at finite bias for several transport regimes: direct tunnelling, Fowler–Nordheim tunnelling and thermionic injection (Figure 8a).88 It was found that TER is present in all three transport regimes with the Fowler–Nordheim active at high bias and thermionic injection at high barrier thickness (Figure 8b). Large TER is favoured in FTJs with thicker barriers in all three transport regimes, but at the cost of current density. The largest TER is predicted when polarisation switching changes the transport regime. Importantly, at finite bias, the TER was shown to be non-zero even for a symmetric junction.
TER at finite bias. (a) Schematic representation of the different transport regimes at finite bias: direct tunnelling (DT), Fowler–Nordheim tunnelling (FNT) and thermionic injection (TI). (b) A contour plot of TER versus applied bias and barrier thickness for an FTJ with following parameters: P=3 μC/cm2, εFE=60 ε0, λL=0.8 Å, λR=0.55 Å, εL=2ε0, εR=8ε0 and U0=1.0 eV. After ref. 88 with permission. (c) Schematic view of the symmetric Au/BaZrO3/Au FTJ and the electrostatic potential profile in the unrelaxed junction for several voltages. After ref. 90 with permission. (d) ON/OFF ratio for the FTJ for the case of electronic screening, electronic and ionic screening, and screening plus piezoelectric response. After ref. 90 with permission.
This result is corroborated by calculations of TER based on a single-orbital tight-binding model, showing that finite bias produces TER in a symmetric junction.89 The effect is due to the change of the effective screening lengths in the electrodes, as the result of the shift in the chemical potential by the applied bias. This conclusion is consistent with the first-principles calculations of TER in Au/BaZrO3/Au FTJs (Figure 8c).90 Under finite applied bias, the junction electrostatic potential, shown in Figure 8c, breaks the symmetry which makes the two polarisation states inequivalent. These results show that at finite bias, the TER is present even in symmetric junctions; however, the slope of the TER curve with bias, in addition to the electronic and ionic screening, depends on the piezoelectric response which appears to produce the largest contribution to TER (Figure 8d).
Multiferroic tunnel junctions
The functionality of FTJs can be extended by using FM electrodes. This kind of FTJ is known as a MFTJ, which can also be considered as a MTJ with a ferroelectric barrier. The key property of a MFTJ is the co-existence of the TMR and TER effects.7,22 Similar to MTJs, the TMR effect arises from the band structure mismatch between the FM electrodes when the magnetisation orientation changes from parallel to antiparallel. The TER effect arises from the asymmetry of the junction breaking the degeneracy between the two polarisation directions. Equivalently these features of MFTJs can be stated as: (i) the presence of four resistance states determined by the mutual orientation of the magnetisation in the electrodes (parallel or antiparallel) and the direction of the polarisation in the barrier or (ii) the tunability of the TMR and TER effects by the complementary ferroic order, that is, there are two values of TMR dependent on ferroelectric polarisation orientation and two values of TER dependent on magnetisation orientation (Figure 9a).
Multiferroic tunnel junctions. (a) Results of model calculations demonstrating the simultaneous presence of TER and TMR effects in a MFTJ: TMR for opposite ferroelectric polarisation orientations in the barrier (top panel), and TER for parallel and antiparallel magnetisation in the electrodes (bottom panel), as a function of ferroelectric polarisation P. After ref. 24 with permission. (b) Resistance as a function of magnetic field in as-grown Co/PZT(3.2 nm)/LSMO junction (black squares) and after polarisation switching (red circles) measured at T=50 K. Magnetisation directions in each magnetic layer and polarisation states of the barrier are schematically shown. After ref. 101 with permission. (c) Spin- and k||-dependent transmission in Co/PTO–ZrO2/Co tunnel junctions for the parallel configuration of magnetic Co electrodes and for the two opposite orientations of ferroelectric polarisation. After ref. 91 with permission. (d) Magnetoelectric coupling in a Co/PTO–ZrO2/Co tunnel junction. Top: difference of the layer-resolved magnetic moments upon reversal of the ferroelectric polarisation in the barrier. Bottom: spin-resolved charge densities for the two ferroelectric polarisations (majority spin—red; minority spin—blue). After ref. 91 with permission.
A number of first-principles calculations have been performed for different MFTJs to elaborate these conclusions.23,59,63,70,91 One of the important outcomes of these calculations is the demonstrated connection between the interfacial magnetoelectric effect and the ferroelectrically controlled TMR effect.92 The reversible electric field induced by the ferroelectric polarisation is predicted to modify the magnetic structure of an adjacent ferromagnet.93–96 On the other hand, the TMR effect is largely determined by the spin-polarised transmission across interfaces,97 and thus by altering the interface spin structure the ferroelectric polarisation affects the spin-polarisation and TMR. For example, the calculated k||-resolved transmission for Co/PbTiO3–ZrO2/Co MFTJs91 shows that the dominant spin contribution to the conductance is switched from majority to minority when the ferroelectric polarisation of PTO is reversed from pointing to the Co/PbO interface to the ZrO2/Co interface (Figure 9c). This effect is explained by the spin density and magnetic moments at the interfaces dependent on ferroelectric polarisation orientation, which constitutes the interface magnetoelectric effect (Figure 9d).91
Experimentally, there have been a number of demonstrations of the co-existence of the TMR and TER effects in MFTJs.98–101 Sizable changes in the negative TMR were observed depending on the orientation of the ferroelectric polarisation in nanoscale Fe/BTO/LSMO and Co/BTO/LSMO MFTJs.98,100 X-ray resonant magnetic scattering indicated that in these junctions there is an induced magnetic moment on the Ti atom that is coupled with the Fe electrode.100 This result, as well as the measured negative spin polarisation of the Fe/BTO interface, is in agreement with first-principles calcuations.93,95 A very large TMR was observed in a LSMO/BTO/LCMO/LSMO MFTJ (Figure 7f).86 The value of TMR was found to be much larger for the junction in a low resistance state (100% at T=80 K) than in a high-resistance state (hardly seen within the noise level). The significantly diminished TMR in the high-resistance state is explained by the LCMO phase transition to the AFM-insulating state.86 Finally, it was shown that switching the ferroelectric polarisation in Co/PZT/LSMO tunnel junctions changes sign of the TMR effect from −3 to +4% (Figure 9b).101 Although the TMR itself was not large, it indicates a possibility to control the sign of the spin polarisation by ferroelectric polarisation.53 Overall, simultaneous TER and TMR effects and their tunability by the complementary ferroic order parameter in MFTJs are consistent with the original theoretical predictions.23
Conclusions and outlook
Overall, the combined effort of theory and experiment has managed to predict, demonstrate and elucidate the fundamental properties of FTJs. The underling physical mechanisms behind the functionality of FTJs are now understood and the figures of merit that have been achieved are remarkable. In particular, the ON/OFF ratios can reach several orders of magnitude and significant scalability and reliability of FTJs have been demonstrated. Thus, FTJs possess a great deal of potential for non-volatile ferroelectric memory applications. In order for ferroelectric memory to become a reality, however, more work is needed in various areas, such as improving the stability of the ferroelectric polarisation in the barrier, controlling and understanding the role of defects such as oxygen vacancies in oxide materials, and understanding the finite bias behaviour of these devices. This is in addition to practical challenges, such as making the manufacturing process scalable and cost-effective for industrial applications and demonstrating the compatibility with existing electronic components.
In terms of future research, there are a number of avenues for development. First, current devices utilise oxide ferroelectrics, such as BTO, PTO and PZT. These materials often contain structural defects, such as oxygen vacancies. Understanding the role of these defects on ferroelectric switching as well as on electronic transport properties of FTJs is of critical importance. Second, the current theoretical methodology, in particular DFT-based calculations, describes very well the effect of the electronic screening of the polarisation and the interface bonding effect at zero bias. However, the finite bias regime and the effects appearing at finite bias are still largely unexplored. Thus, methodology improvements to target these regimes are necessary. Third, a potentially interesting research direction is the extension of the functionality of the devices using more complex materials with multiple and possibly coupled ferroic orders, such as single-phase magnetoelectric multiferroics. Finally, exploration of other ferroelectric materials, such as organic ferroelectrics that could preserve ferroelectricity at monolayer thickness, would be interesting.
References
Frenkel, J. On the electrical resistance of contacts between solid conductors. Phys. Rev. 36, 1604–1618 (1930).
Chappert, C., Fert, A. & Van Dau, F. N. The emergence of spin electronics in data storage. Nat. Mater. 6, 813–823 (2007).
Jullière, M. Tunneling between ferromagnetic films. Phys. Lett. A 54, 225–226 (1975).
Tsymbal, E. Y., Mryasov, O. N. & LeClair, P. R. Spin-dependent tunnelling in magnetic tunnel junctions. J. Phys. Condens. Matter 15, R109–R142 (2003).
Zubko, P., Gariglio, S., Gabay, M., Ghosez, P. & Triscone, J.-M. Interface physics in complex oxide heterostructures. Annu. Rev. Condens. Matter Phys. 2, 141–165 (2011).
Bibes, M., Villegas, J. E. & Barthélémy, A. Ultrathin oxide films and interfaces for electronics and spintronics. Adv. Phys. 60, 5 (2011).
Tsymbal, E. Y. & Kohlstedt, H. Tunneling across a ferroelectric. Science 313, 181–183 (2006).
Velev, J. P., Jaswal, S. S. & Tsymbal, E. Y. Multiferroic and magnetoelectric materials and interfaces. Phil. Trans. R. Soc. A 369, 3069–3097 (2011).
Rabe, K. M., Dawber, M., Lichtensteiger, C., Ahn, C. H., Triscone, J.-M. in Topics in Applied Physics 105, 1–30 (eds Rabe K., Ahn C. H. & Triscone J.-M. ) (Springer-Verlag, Berlin, Heidelberg, Germany, 2007).
Horiuchi, S. & Tokura, Y. Organic ferroelectrics. Nat. Mater. 7, 357–366 (2008).
Esaki, L., Laibowitz, R. B. & Stiles, P. J. Polar switch. IBM Tech. Discl. Bull. 13, 2161–2162 (1971).
Ahn, C. H., Rabe, K. M. & Triscone, J.-M. Ferroelectricity at the nanoscale: local polarization in oxide thin films and heterostructures. Science 303, 488–491 (2004).
Dawber, M., Rabe, K. M. & Scott, J. F. Physics of thin-film ferroelectric oxides. Rev. Mod. Phys. 77, 1083–1130 (2005).
Junquera, J. & Ghosez, P. Critical thickness for ferroelectricity in perovskite ultrathin films. Nature 422, 506–509 (2003).
Fong, D. D. et al. Ferroelectricity in ultrathin perovskite films. Science 304, 1650–1653 (2004).
Lichtensteiger, C., Triscone, J.-M., Junquera, J. & Ghosez, P. Ferroelectricity and tetragonality in ultrathin PbTiO3 films. Phys. Rev. Lett. 94, 047603 (2005).
Tenne, D. A. et al. Probing nanoscale ferroelectricity by ultraviolet raman spectroscopy. Science 313, 1614 (2006).
Zhuravlev, M. Y., Sabirianov, R. F., Jaswal, S. S. & Tsymbal, E. Y. Giant electroresistance in ferroelectric tunnel junctions. Phys. Rev. Lett. 94, 246802 (2005).
Kohlstedt, H., Pertsev, N. A., Rodríguez Contreras, J. & Waser, R. Theoretical current-voltage characteristics of ferroelectric tunnel junctions. Phys. Rev. B 72, 125341 (2005).
Velev, J. P., Duan, C.-G., Belashchenko, K. D., Jaswal, S. S. & Tsymbal, E. Y. Effect of ferroelectricity on electron transport in Pt/BaTiO3/Pt tunnel junctions. Phys. Rev. Lett. 98, 137201 (2007).
Tsymbal, E. Y. & Gruverman, A. Ferroelectric tunnel junctions: Beyond the barrier. Nat. Mater. 12, 602–604 (2013).
Zhuravlev, M. Y., Jaswal, S. S., Tsymbal, E. Y. & Sabirianov, R. F. Ferroelectric switch for spin injection. Appl. Phys. Lett. 87, 222114 (2005).
Velev, J. P. et al. Magnetic tunnel junctions with ferroelectric barriers: Prediction of four resistance states from first principles. Nano Lett. 9, 427–432 (2009).
Zhuravlev, M. Y., Maekawa, S. & Tsymbal, E. Y. Effect of spin-dependent screening on tunneling electroresistance and tunneling magnetoresistance in multiferroic tunnel junctions. Phys. Rev. B 81, 104419 (2010).
Tsymbal, E. Y., Gruverman, A., Garcia, V., Bibes, M. & Barthélémy, A. Ferroelectric and multiferroic tunnel junctions. MRS Bull. 37, 138–143 (2012).
Garcia, V. & Bibes, M. Ferroelectric tunnel junctions for information storage and processing. Nat. Commun. 5, 4289 (2014).
Mehta, R. R., Silverman, B. D. & Jacobs, J. T. Depolarization fields in thin ferroelectric films. J. Appl. Phys. 44, 3379–3385 (1973).
Kim, D. J. et al. Polarization relaxation induced by a depolarization field in ultrathin ferroelectric BaTiO3 capacitors. Phys. Rev. Lett. 95, 237602 (2005).
Simmons, J. G. Generalized formula for the electric tunnel effect between similar electrodes separated by a thin insulating film. J. Appl. Phys. 34, 1793–1803 (1963).
Brinkman, W. F., Dynes, R. C. & Rowell, J. M. Tunneling conductance of asymmetric barriers. J. Appl. Phys. 41, 1915–1921 (1970).
Gruverman, A. et al. Tunneling electroresistance effect in ferroelectric tunnel junctions at nanoscale. Nano Lett. 9, 3539–3543 (2009).
Sokolov, A., Bak, O., Lu, H., Tsymbal, E. Y. & Gruverman, A. Effect of epitaxial strain on tunneling electroresistance in ferroelectric tunnel junctions. Nanotechnology 25, 305202 (2015).
Garcia, V. et al. Giant tunnel electroresistance for non-destructive readout of ferroelectric states. Nature 460, 81–84 (2009).
Maksymovych, P., Jesse, S., Yu, P., Ramesh, R., Baddorf, A. P. & Kalinin, S. V. Polarization control of electron tunneling into ferroelectric surfaces. Science 324, 1421–1425 (2009).
Li, Z. et al. An epitaxial ferroelectric tunnel junction on silicon. Adv. Mater. 26, 7185–7189 (2014).
Pantel, D., Goetze, S., Hesse, D. & Alexe, M. Room-temperature ferroelectric resistive switching in ultrathin Pb(Zr0.2Ti0.8)O3 films. ACS Nano 5, 6032–6038 (2011).
Chanthbouala, A. et al. Solid-state memories based on ferroelectric tunnel junctions. Nat. Nanotechnol. 7, 101–104 (2012).
Zenkevich, A. et al. Electronic band alignment and electron transport in Cr/BaTiO3/Pt ferroelectric tunnel junctions. Appl. Phys. Lett. 102, 062907 (2013).
Boyn, S. et al. Engineering ferroelectric tunnel junctions through potential. APL Mater. 3, 061101 (2015).
Soni, R. et al. Giant electrode effect on tunneling electroresistance in ferroelectric tunnel junctions. Nat. Commun. 5, 5414 (2014).
Liu, X., Wang, Y., Burton, J. D. & Tsymbal, E. Y. Polarization-controlled Ohmic to Schottky transition at a metal/ferroelectric interface. Phys. Rev. B 88, 165139 (2013).
Liu, X., Burton, J. D., Zhuravlev, M. Y. & Tsymbal, E. Y. Electric control of spin injection into a ferroelectric semiconductor. Phys. Rev. Lett. 114, 046601 (2015).
Liu, X., Burton, J. D. & Tsymbal, E. Y. Enhanced tunneling electroresistance in ferroelectric tunnel junctions due to the reversible metallization of the barrier. Phys Rev. Lett. 116, 197602 (2016).
Wen, Z., Li, C., Wu, D., Li, A. & Ming, N. Ferroelectric-field-effect-enhanced electroresistance in metal/ferroelectric/semiconductor tunnel junction. Nat. Mater. 12, 617–621 (2013).
Li, C. et al. Ultrathin BaTiO3‑based ferroelectric tunnel junctions through interface engineering. Nano Lett. 15, 2568–2573 (2015).
Radaelli, G. et al. Large room-temperature electroresistance in dual-modulated ferroelectric tunnel barriers. Adv. Mater. 27, 2602–2607 (2015).
Quindeau, A. et al. Origin of tunnel electroresistance effect in PbTiO3-based multiferroic tunnel junctions. Phys. Rev. B 92, 035130 (2015).
Martin, R. M. Electronic Structure: Basic Theory and Practical Methods. (Cambridge University Press, Cambridge, UK, 2008).
Singh-Miller, N. E. & Marzari, N. Surface energies, work functions, and surface relaxations of low-index metallic surfaces from first principles. Phys. Rev. B 80, 235407 (2009).
Gerra, G., Tagantsev, A. K., Setter, N. & Parlinski, K. Ionic polarizability of conductive metal oxides and critical thickness for ferroelectricity in BaTiO3 . Phys. Rev. Lett. 96, 107603 (2006).
Stengel, M., Vanderbilt, D. & Spaldin, N. A. Enhancement of ferroelectricity at metal-oxide interfaces. Nat. Mater. 8, 392–397 (2009).
Shen, L. et al. Systematic study of ferroelectric, interfacial, oxidative, and doping effects on conductance of Pt/BaTiO3/Pt ferroelectic tunnel junctions. Phys. Rev. B 85, 064105 (2012).
Velev, J. P., Lopez-Encarnacion, J. M., Burton, J. D. & Tsymbal, E. Y. Multiferroic tunnel junctions with poly(vinylidene fluoride). Phys. Rev. B 85, 125103 (2012).
Velev, J. P. et al. Negative spin polarization and large tunneling magnetoresistance in epitaxial Co/SrTiO3/Co magnetic tunnel junctions. Phys. Rev. Lett. 95, 216601 (2005).
Kohn, W. Analytic properties of Bloch waves and Wannier functions. Phys. Rev 115, 809 (1959).
Heine, V. On the general theory of surface states and scattering of electrons in solids. Proc. Phys. Soc. 81, 300 (1963).
Mavropoulos, P., Papanikolaou, N. & Dederichs, P. Complex band structure and tunneling through ferromagnet/insulator/ferromagnet junctions. Phys. Rev. Lett. 85, 1088 (2000).
Butler, W. H., Zhang, X.-G., Schulthess, T. C. & MacLaren, J. M. Spin-dependent tunneling conductance of Fe/MgO/Fe sandwiches. Phys. Rev. B 63, 054416 (2001).
Caffrey, N. M., Archer, T., Rungger, I. & Sanvito, S. Prediction of large bias-dependent magnetoresistance in all-oxide magnetic tunnel junctions with a ferroelectric barrier. Phys. Rev. B 83, 125409 (2011).
Hinsche, N. F. et al. Strong influence of complex band structure on tunneling electroresistance: A combined model and ab initio study. Phys. Rev. B 82, 214110 (2010).
Wortmann, D. & Blügel, S. Influence of the electronic structure on tunneling through ferroelectric insulators: Application to BaTiO3 and PbTiO3 . Phys. Rev. B 83, 155114 (2011).
Aguado-Puente, P. & Junquera, J. First-principles study of metal-induced gap states in metal/oxide interfaces and their relation with the complex band structure. MRS Commun. 3, 191–197 (2013).
Dai, J.-Q., Zhang, H. & Song, Y.-M. Magnetoelectric coupling and spin-dependent tunneling in Fe/PbTiO3/Fe multiferroic heterostructure with a Ni monolayer inserted at one interface. J. Appl. Phys. 118, 054104 (2015).
Landauer, R. Electrical resistance of disordered one-dimensional lattices. Philos. Mag. 21, 863–867 (1970).
Brandbyge, M., Mozos, J.-L., Ordejon, P., Taylor, J. & Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 65, 165401 (2002).
Choi, H. J. & Ihm, J. Ab initio pseudopotential method for the calculation of conductance in quantum wires. Phys. Rev. B 59, 2267–2275 (1999).
Smogunov, A., Dal Corso, A. & Tosatti, E. Ballistic conductance of magnetic Co and Ni nanowires with ultrasoft pseudopotentials. Phys. Rev. B 70, 045417 (2004).
Caroli, C., Combescot, R., Nozieres, P. & Saint-James, D. Direct calculation of the tunneling current. J. Phys. C 4, 916 (1971).
Velev, J. & Butler, W. On the equivalence of different techniques for evaluating the Green function for a semi-infinite system using a localized basis. J. Phys. Cond. Mater. 16, R637 (2004).
López-Encarnación, J. M., Burton, J. D., Tsymbal, E. Y. & Velev, J. P. Organic multiferroic tunnel junctions with ferroelectric poly(vinylidene fluoride) barriers. Nano Lett. 11, 599–603 (2011).
Gerra, G., Tagantsev, A. K. & Setter, N. Ferroelectricity in asymmetric metal-ferroelectric-metal heterostructures: a combined first-principles-phenomenological approach. Phys. Rev. Lett. 98, 207601 (2007).
Liu, X., Wang, Y., Lukashev, P. V., Burton, J. D. & Tsymbal, E. Y. Interface dipole effect on thin film ferroelectric stability: First-principles and phenomenological modeling. Phys. Rev. B 85, 125407 (2012).
Lu, H. et al. Enhancement of ferroelectric polarization stability by interface engineering. Adv. Mater. 24, 1209–1216 (2012).
Yamada, H. et al. Strong surface-termination effect on electroresistance in ferroelectric tunnel junctions. Adv. Funct. Mater. 25, 2708–2714 (2015).
Zhuravlev, M. Y., Wang, Y., Maekawa, S. & Tsymbal, E. Y. Tunneling electroresistance in ferroelectric tunnel junctions with a composite barrier. Appl. Phys. Lett. 95, 052902 (2009).
Caffrey, N. M., Archer, T., Rungger, I. & Sanvito, S. Coexistance of giant tunneling electroresistance and magnetoresistance in an all-oxide composite magnetic tunnel junction. Phys. Rev. Lett. 109, 226803 (2012).
Chen, Y. & McIntyre, P. C. Effects of chemical stability of platinum/lead zirconate titanate and iridium oxide/lead zirconate titanate interfaces on ferroelectric thin film switching reliability. Appl. Phys. Lett. 91, 232906 (2007).
Wang, R. V. et al. Reversible chemical switching of a ferroelectric film Phys. Rev. Lett. 102, 047601 (2009).
Lu, H. et al. Ferroelectric tunnel junctions with graphene electrodes. Nat. Commun. 5, 5518 (2014).
Dagotto, E., Hotta, T. & Moreo, A. Colossal magnetoresistant materials: the key role of phase separation. Phys. Rep. 344, 1–153 (2001).
Burton, J. D. & Tsymbal, E. Y. Prediction of electrically induced magnetic reconstruction at the manganite/ferroelectric interface. Phys. Rev. B 80, 174406 (2009).
Burton, J. D. & Tsymbal, E. Y. Giant tunneling electroresistance effect driven by an electrically controlled spin valve at a complex oxide interface. Phys. Rev. Lett. 106, 157203 (2011).
Molegraaf, H. J. A. et al. Magnetoelectric effects in complex oxides with competing ground states. Adv. Mater. 21, 3470–3474 (2009).
Park, J. H. et al. Direct evidence for a half-metallic ferromagnet. Nature 392, 794–796 (1998).
Vaz, C. A. F. et al. Origin of the magnetoelectric coupling effect in Pb(Zr0.2Ti0.8)O3/La0.8Sr0.2MnO3 multiferroic heterostructures. Phys. Rev. Lett. 104, 127202 (2010).
Yin, Y. W. et al. Enhanced tunnelling electroresistance effect due to a ferroelectrically induced phase transition at a magnetic complex oxide interface. Nat. Mater. 12, 397 (2013).
Jiang, L. et al. Tunneling electroresistance induced by interfacial phase transitions in ultrathin oxide heterostructures. Nano Lett. 13, 5837–5843 (2013).
Pantel, D. & Alexe, M. Electroresistance effects in ferroelectric tunnel barriers. Phys. Rev. B 82, 134105 (2010).
Useinov, A., Kalitsov, A., Velev, J. & Kioussis, N. Bias-dependence of the tunneling electroresistance and magnetoresistance in multiferroic tunnel junctions. Appl. Phys. Lett. 105, 102403 (2014).
Bilc, D. I., Novaes, F. D., Íñiguez, J., Ordejón, P. & Ghosez, P. Electroresistance effect in ferroelectric tunnel junctions with symmetric electrodes. ACS Nano 6, 1473–1478 (2012).
Borisov, V. S., Ostanin, S., Achilles, S., Henk, J. & Mertig, I. Spin-dependent transport in a multiferroic tunnel junction: Theory for Co/PbTiO3/Co. Phys. Rev. B 92, 075137 (2015).
Burton, J. D. & Tsymbal, E. Y. Magnetoelectric interfaces and spin transport. Philos. Trans. A Math. Phys. Eng. Sci. 370, 4840–4855 (2012).
Duan, C. G., Jaswal, S. S. & Tsymbal, E. Y. Predicted magnetoelectric effect in Fe/BaTiO3 multilayers: ferroelectric control of magnetism. Phys. Rev. Lett. 97, 047201 (2006).
Yamauchi, K., Sanyal, B. & Picozzi, S. Interface effects at a half-metal/ferroelectric junction. Appl. Phys. Lett. 91, 062506 (2007).
Fechner, M. et al. Magnetic phase transition in two-phase multiferroics predicted from first principles. Phys. Rev. B 78, 212406 (2008).
Niranjan, M. K., Burton, J. D., Velev, J. P., Jaswal, S. S. & Tsymbal, E. Y. Magnetoelectric effect at the SrRuO3/BaTiO3 (001) interface: An ab initio study. Appl. Phys. Lett. 95, 052501 (2009).
Belashchenko, K. D. et al. Effect of interface bonding on spin-dependent tunneling from the oxidized Co surface. Phys. Rev. B 69, 174408 (2004).
Garcia, V. et al. Ferroelectric control of spin polarization. Science 327, 1106–1110 (2010).
Hambe, M. et al. Crossing an interface: Ferroelectric control of tunnel currents in magnetic complex oxide heterostructures. Adv. Funct. Mater. 20, 2436–2441 (2010).
Valencia, S. et al. Interface-induced room-temperature multiferroicity in BaTiO3 . Nat. Mater. 10, 753 (2011).
Pantel, D., Goetze, S., Hesse, D. & Alexe, M. Reversible electrical switching of spin polarization in multiferroic tunnel junctions. Nat. Mater. 11, 289–293 (2012).
Acknowledgements
This work was supported by the National Science Foundation (NSF) through Materials Research Science and Engineering Center (MRSEC, grant no. DMR-1420645) and the Semiconductor Research Corporation through Center for NanoFerroic Devices (CNFD). The work at UPR was supported by NSF (grants nos EPS-1010094 and DMR-1105474). We thank Verona Skomski for her help in preparation of the manuscript for submission.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Velev, J., Burton, J., Zhuravlev, M. et al. Predictive modelling of ferroelectric tunnel junctions. npj Comput Mater 2, 16009 (2016). https://doi.org/10.1038/npjcompumats.2016.9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/npjcompumats.2016.9
This article is cited by
-
Resistive switching and Schottky barrier modulation at CoPt/ ferroelectric-like MgZnO interface for non-volatile memories
Journal of Materials Science: Materials in Electronics (2024)
-
Greatly enhanced tunneling electroresistance in ferroelectric tunnel junctions with a double barrier design
npj Computational Materials (2023)
-
In-plane ferroelectric tunnel junctions based on 2D α-In2Se3/semiconductor heterostructures
npj Computational Materials (2023)
-
Electrical switching of spin-polarized current in multiferroic tunneling junctions
npj Computational Materials (2022)
-
Integration of resonant band with asymmetry in ferroelectric tunnel junctions
npj Computational Materials (2022)