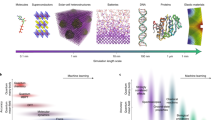
Abstract
Recent technical advances in the area of nanoscale imaging, spectroscopy and scattering/diffraction have led to unprecedented capabilities for investigating materials structural, dynamical and functional characteristics. In addition, recent advances in computational algorithms and computer capacities that are orders of magnitude larger/faster have enabled large-scale simulations of materials properties starting with nothing but the identity of the atomic species and the basic principles of quantum and statistical mechanics and thermodynamics. Along with these advances, an explosion of high-resolution data has emerged. This confluence of capabilities and rise of big data offer grand opportunities for advancing materials sciences but also introduce several challenges. In this perspective, we identify challenges impeding progress towards advancing materials by design (e.g., the design/discovery of materials with improved properties/performance), possible solutions and provide examples of scientific issues that can be addressed using a tightly integrated approach where theory and experiments are linked through big-deep data.
Similar content being viewed by others
Introduction
The ability to design and refine materials has long accentuated the development of technology and infrastructure. Dating back to the introduction of stone (which ended not due to the lack of the availability of stone but due to a better material, bronze), bronze and iron (interestingly, iron was introduced due to availability, not because it was a better material) are historical milestones that shaped the development of cultures and the rise and fall of civilisations. More recently, examples of materials milestones include the Murano glass and Meissen porcelain that enabled the rise of medieval trade, technological and economic powerhouses and the quality of steel that generated the difference between Japanese and Chinese fencing styles and found deep reflections in culture. In all these cases, the natural availability of the particular raw material, and often serendipitous or brute force know-how, made a significant imprint on cultures and determined the rate of progress and destinies of people and countries. Materials shape and define the societies of their time: much as it is impossible to imagine a Samurai without a sword, presently, it is now difficult to imagine a person without a cell phone.
The ever-increasing spectrum of important functionalities required for developing and optimising materials fundamental to our modern requirements1–3 (e.g., modern smart phones have up to 75 different elements compared with twentieth century version that had ~30) requires efficient paradigms for materials discovery and design that go beyond our current serendipitous discoveries and classical synthesis characterisation theory approaches.4 This is because structures and composition underpinning the next-generation materials are not well understood, much less the pathways to synthesise them.5–11
As an example of the current problem, MgB2 was known to exist for decades but it was only recently discovered to be a superconducting material. Similarly, although a huge family of materials existed in layered geometries, only after the discovery of how to exfoliate graphite has it been possible to even consider monolayered materials leading to novel discoveries such as monolayer Fe-chalcogenide (highest Tc among all Fe-based superconductors), functionalised monolayer h-BN (piezoelectric), monolayer MoS2 (tunable band gap with high conductivity) and so on. Another critical example comes from complex oxides, the building blocks of many real-world devices. Bulk oxides with couplings between many degrees of freedom have been studied for many years with the hopes of finding a true multiferroic device12–14—one in which an electric field can manipulate magnetic properties or a magnetic field can the internal electric dipole or polarisation. Such materials would offer numerous benefits, such as the possibility of next-generation, low-power-consumption storage devices.15–18 However, only one material, BiFeO3, exhibits robust multiferroic properties at room temperature (and was discovered serendipitously).19–22 Recent efforts have been geared towards harnessing emergent phenomena at oxide heterostructure interfaces to build transistors and next-generation storage devices.23–26 Thin-film and heterostructure interfaces offer a wide variety of controllable variables that (in principle) permit design—choice of ‘parent’ material (or multiple materials for heterostructures), strains in the thin-film forms, composition changes at surfaces and interfaces (including defects such as oxygen vacancies) and dopant control of carrier concentrations.
Bridging these complex issues will require integrated and direct feedback from multi-scale functional measurements to theory and must allow real-time and archival experimental data to be incorporated effectively. Although computational approaches have recently allowed screening bulk properties of materials in existing structures in the inorganic (or organic) crystal structure databases, these efforts often lack a concerted effort to understand how a particular functionality comes about in a compound (or a set of compounds) and to use this knowledge to discover new materials and to provide a means of accessing the synthesis pathways. There are at least three major gaps that need to be addressed to enable more rapid progress for designing materials with desired properties.
First, there is the need for enhanced reliability for the computational techniques in such a way that they can accurately (and rapidly) address the above complex functionalities, provide the precision necessary for discriminating between closely competing behaviours and capability of achieving the length scales necessary to bridge across features such as domain walls, grain boundaries and gradients in composition. By and large, currently used theory-based calculations lack a reliable accuracy, and cannot treat the multiple length and time scales required. True materials are far more complicated than the simple structures often studied in small periodic unit cells by electronic structure calculations. The large length and time scales, as well as finite temperatures, make even density functional theory (DFT) calculations for investigating materials under device-relevant conditions prohibitively expensive. Grain boundaries, extended defects and complex heterostructures further complicate this issue.
Second, there is a need to take full advantage of all of the information contained in experimental data to provide input into computational methods to predict and understand new materials. This includes integrating data efficiently from different characterisation techniques to provide a more complete perspective on materials structure and function. For example, scanning probe microscopy reveals position-dependent functionality data, whereas transmission electron microscopy provides position-dependent electronic structure information—including behaviour near the above-mentioned defects that directly affect materials functionality. Techniques such as inelastic neutron scattering allow for direct measurements of space- and time-dependent response functions, which in principle can be compared directly with theoretical calculations. However, many of these techniques come with extreme requirements for full analysis and utilisation of instrumental data. For example, modern time-of-flight spectroscopy results in huge data sets, and in common with microscopy enormous amounts of potentially insightful experimental data are generated, which remain largely unreported and unused.
Third, pathways for making materials need to be established. Although in general pathways for making materials are least amenable to theoretical exploration and primarily rely on the expertise of individual researchers, big-data analytics on existing bodies of knowledge on synthesis pathways can suggest the general correlations between materials properties and synthetic routes, suggesting specific research directions.
In this perspective, we outline a strategy for bridging these critical gaps through utilisation of petascale quantum simulation, data assimilation and data analysis tools for functional materials design, in an approach that includes uncertainty quantification and experimental validation (Figure 1). This approach to change the past synthesis→characterisation→theory paradigm requires addressing gaps as a scientific community rather than relying upon tools used within a specific group, further necessitating development of efficient community-wide tools and data, including scientometric and text analytics.27–30 Ideally, these tools need to be easily used by, and to the greatest extent, freely available to the scientific community, and in a framework that allows the community to contribute. We argue that transformative breakthroughs in materials design will depend on the availability of high-end simulation software and data analytics approaches that can fully utilise unparalleled resources in computing power and availability of data.
Development and integration of theoretical tools
During the past couple of decades, theory and simulation have been reasonably successful in predicting single materials functionalities. However, the Materials Genome Initiative,31 calls for understanding, designing and predicting materials with ‘competing functionalities’ that often give rise to inhomogeneous ground states and chemical disorder. From occupancy in equivalent or weakly nonequivalent positions, to chemical phase separation in physically inhomogeneous systems (manganites, high-temperature superconductors (HTSCs)), we must be able to treat these mixed degrees of freedom. This could provide a route for rapid screening by first-principle methods of realistic materials structures incorporating the complexities of real materials, such as extended defects and impurities, as well as the complexities due to electron correlation and proximities to phase transitions. Achieving this goal will require a foundation-based quantum approaches that is capable of performing at peta- or even exascale levels, a framework for high-throughput calculations of multiple configurations and structures, and extensive data assimilation, validation and uncertainty quantification capabilities.
First-principle computational approaches
Starting with DFT, the current methods generally fall into a few groups: those using pseudopotentials and all-electron methods. Pseudopotential methods include plane-wave-based codes (QUANTUM ESPRESSO32, VASP21, Qbox33 and ABINIT34), where wave functions are expanded in a linear combination of plane waves and the Kohn–Sham equation is solved in Fourier space. Alternatively, the wave functions can be expanded in a linear combination of localised orbitals (e.g., atomic orbitals as basis set in the SIESTA package35). Gaussian packages, mainly used in the chemistry community, employ Gaussians as the basis set or different localisations (such as GAMESS36, NWChem37 and GAUSSIAN38). For all-electron methods, a direct analogy is the method based on augmented plane waves,39,40 versus methods based on radial basis sets.39,41–43 In addition, multiple-scattering theory allows the formulation of all-electron Kohn–Korringa–Rostoker methods44 that do not rely on the expansion of the orbitals into basis functions, but directly calculate the Green’s function of the electrons in the system. In another group, the wave functions are represented directly on real-space grids. This approach is used in real-space multigrid45,46, PARSEC47 and GPAW48 codes. In general, real-space codes can be more easily scaled to a large number of message passing interface processes using domain decomposition, because the required message passing interface communications are mostly among neighbouring nodes. In plane wave codes, the required fast Fourier transforms require all-to-all communications, which are hard to scale to a large number of nodes. At this point in time, all major DFT packages have been adapted to work on parallel architectures at some level, but generally not on petascale level or hybrid architectures.
To make the transformative advances needed to achieve materials by design, another level of computational capability and validated accuracy would be valuable. However, one could argue that it is not as simple as enabling larger-scale calculations, but it may require a ‘disruptive’ advance in theory, such as the one brought about by DFT itself. In fact, one possibility might be based on the reformulation of ab initio computational methods to use many-electron basis states instead of one-electron basis states, e.g., many-body theory and computational methods that overcomes the limitation of current one-electron basis approaches could be revolutionary. Further work along these lines is clearly needed.
Turning back to current forms of DFT, one approach forward can be to build on real-space codes that have demonstrated petascale performance.45–50 However, it will be important that these efforts include a robust common user interface for community use, and new capabilities necessary to enable treatment of important materials functionalities. The bridge between such atomistic computations and timely predictions might be realised by training complex models using the copious amounts of atomistic computations that are linked with the big data available from imaging and spectroscopy and bulk synchrotron X-ray and neutron measurements. Although such machine learning-based models are slowly beginning to make their way into the area of materials science, either in the form of unsupervised learning algorithms to fit the exchange-correlation functional, or supervised learning to predict electronic properties of molecular systems, more work is required to combine these techniques with experimental data to improve their predictive capability.51–59
Accurate models for microstructure will be required in order to predict across scales relevant to materials under device-relevant conditions. Treating the longer length scales can often be achieved with tight-binding simulations,60–65 effective Hamiltonians66–70 or suitably tailored reactive and/or coarse-gained models. The value of tight binding and effective Hamiltonians is they are easily parameterised by first-principle calculations and preserve the ability to resolve electronic structure and chemical processes. For example, these approaches can address whether or not predicted zero-Kelvin structures and magnetic moments/ferroelectric polarisations persist to higher temperatures and, if not, do the materials remain useful.66,69,71,72 One can also study domain wall dynamics, including domain wall motion and energies as a function of simulation temperature, as well as issues of oxygen vacancies and their segregation to domains walls, as required for enabling device applications, as well as understanding switching and fatigue.68,73–79 To enhance the computational abilities of effective Hamiltonian methods, implementation of the Wang–Landau (WL) Monte Carlo80 and the Hybrid Monte Carlo81 algorithms shows good promise. Combined with the use of the massively parallel supercomputers, this can enable calculations of finite temperature properties using supercells containing up to 108–109 atoms. Such capabilities allow study of complex effects with the potential to discover revolutionary complex (e.g., disordered) materials for which THz electro-optic coefficients (related to a change of the refractive index in response to an applied dc electric field) and/or THz dielectric tunability could be optimised. Having large electro-optic coefficients and/or large dielectric tunability could improve design of, e.g., efficient communication devices, such as phase arrays, phase shifters and external modulators operating in the THz range.
Integration with big-data approaches to bridge with experiments
In order to move beyond these theory-based avenues for improved capabilities in accuracies and scales, we must begin to fully utilise the spectacular progress over the past 10 years in imaging, X-ray and neutron scattering, which together provide quantitative structural and functional information from the atomic scale to the relevant mesoscales where real-world functionality often emerges. However, work is required to harness this as it frequently involves complex multidimensional data that require statistical approaches, decorrelation, clustering and visualisation techniques generally referred to as big-data approaches. Establishing a workflow for data and imaging analysis to provide the relevant atomic and magnetic configurations, as well as response behaviours of materials for direct input into the first-principle simulations, and subsequent refinement of theoretical parameters via iterative feedback. This approach also will need to be extended to interactive knowledge discovery that ultimately can deliver direct manipulation and design of materials. We suggest that data from state-of-the-art imaging, spectroscopy and scattering approaches integrated with theory can significantly improve the quality and rate of theoretical predictions for accelerating the design and discovery of functional materials.82
In terms of real-space imaging as a quantitative structural and functional tool, recent progress in high-resolution, real-space imaging techniques such as scanning transmission electron microscopy (STEM),83–85 scanning tunnelling microscopy (STM)86,87 and non-contact atomic force microscopy (AFM) have allowed direct imaging of atomic columns (with STEM) and surface atomic structures (with STM/AFM). Going beyond the detection of atomic positions, high-resolution STEM, STM and non-contact AFM provide real-space electronic structure of materials and surfaces, visualising structures of molecular vibrations and phonons, complex electronic phenomena in graphene and high-temperature superconductors88,89 and even chemical bonds—thus relating structural parameters to local functionality. Just as the theoretical predictions are moving beyond the description of a material as repeated unit cell in a perfect crystal, experimental techniques are capable of detecting local disorder. Single STEM ptychography provides a wealth of information in k-space, often with 10 nm (X-ray) and atomic spatial resolution (STEM). Scanning, electron, X-ray and neutron probes enable a broad range of spectroscopies and provide information on local electronic, dielectric and chemical properties (e.g., electron energy loss spectroscopy in STEM, EXAFS or dichroism in X-rays, phonons in inelastic neutron scattering); the resulting data sets are multidimensional. Using this structural and functional information offers a unique opportunity to explore structure–property relationships on a level of a single atom and chemical bond, thereby linking local electronic, magnetic and superconductive functionalities to local bond lengths and angles.
Finally, microscopy tools can be used to arrange atoms in desired configurations, controlling matter via current- and force-based scanning probes90 and electron beams,91 opening a pathway to explore non-equilibrium and high-energy states generally unavailable in the macroscopic form but often responsible for materials functionalities.92 This can therefore complete a full loop in the materials discovery and design cycle, from exquisite observation to theory-based prediction, and finally to experimental control of materials. By combining atomic scale information from imaging with mesoscale and dynamical information from neutrons and chemical information from time-of-flight secondary ion mass spectrometry (such as AFM-TOF-SIMS)—giving the ability to probe deeper into the bulk of the material and look at buried interfaces and so on—via modelling provides a comprehensive approach to understand the complex behaviour of materials.
A more enabling aspect of theory–experiment matching is to improve a theoretical model given experimental observations. On the qualitative level, this is what imaging provides—namely, direct observation of atomic configurations that gives more information on local structures, defects, interfaces and so on (Figure 2). On a semi-quantitative level, the numerical values of observed atomic spacing’s can indicate the incompleteness of the model—e.g., the presence of (invisible) light atoms93 or vacancies.94 However, virtually unexplored is the potential of the quantitative studies—i.e., to improve the parameters of the mesoscopic or quantum theory based on these types of high-quality experimental observations of multiple spatially distributed degrees of freedom.
Quantitative imaging allows access to a broad range of local structure–property relationships within each sample, effectively probing a combinatorial library of defects and functionalities. Whereas macroscopic properties yield information on single points in chemical space, local measurements can provide similar information for multiple points in chemical space. This information, when suitably processed, can be directly linked to theoretical simulations to enable effective exploration of material behaviours and properties. Furthermore, knowledge of extant defect configurations in solid can significantly narrow the spectrum of atomic configurations to be probed theoretically, precluding exponential growth of number of possible configurations with system size.
In reciprocal space (k-space), integration of big-data analytics and the unique capabilities for neutron- and X-ray-based imaging and spectroscopy of magnetic, inelastic and vibrational properties of materials offers equally interesting and enabling capabilities. For example, existing instrument suites for neutron scattering enables significant ability to comprehensively map out the dynamical response in materials across wide temporal and spatial scales. Data sets that are quantitative and complete in terms of coverage of the full-frequency scale of the system and wavevectors spanning the entire Brillouin zone give a broad resource for experimentally validating computation. Indeed, the dynamics in well-defined and highly characterised systems provide very stringent tests of approximations as the dispersion, intensity and line shapes are sensitive to the orbital overlaps, electron correlations and level of itinerancy. Further, a quantitative description of the dynamical response is directly related to transport and functional properties of the materials. First-principle calculations of the inelastic neutron scattering, e.g., for the spin cross-section S(q,ω) can be directly compared with measurement. By providing a comprehensive set of tools at different levels of approximation, there is potential to considerably extend the scope of analysis beyond the more localised magnetic systems commonly studied to itinerant behaviours for which data can offer new and essential insight.
Completing the materials by design loop
Both real-space and k-space imaging provide can provide information that can significantly improve material predictions. Indeed, real- and k-space observations can provide information on the predominant types of the defects and atomic configurations in the materials, which can be used to narrow the range of theoretically explored atomic configurations. Similarly, local structure–property measurements can be used to verify and improve theoretical models, as discussed elsewhere.82 However, an even bigger challenge is offered by comparing the theory with experiment on the level of microscopic degrees of freedom.
An approach to build an efficient computational interface between big data, experiment and theory that can provide an effective tool for advancing materials by design can benefit from a descriptor-based approach (Figure 3). Descriptors are functions of calculable microscopic quantities (e.g., formation energies, band structure, density of states or magnetic moments) that connect experimentally measurable quantities to local or macroscopic properties. Descriptors can represent macroscopic properties of the materials such as mobility, susceptibility or critical temperature. Therefore, a microscopic understanding of physical processes and mechanism is a requisite for defining a physically and structurally meaningful descriptor. A descriptor of a given materials property can be found either by physical intuition or by data mining such as machine learning and clustering analysis. Unfortunately, the concept of descriptors is well introduced in only a couple of problems such as predicting the crystal structure of an alloy, searching for a topological insulator, estimating a crystal’s melting point, and finding the optimal composition of heterogeneous catalysts.51,95 Successful examples of descriptors include formation enthalpy as a descriptor for determining the thermodynamic stabilities of binary and ternary compounds,52 spectroscopic limited maximum efficiency as a descriptor for evaluating the performance of solar materials,96 and figure of merit, ZT, as a descriptor for evaluating the performance of thermoelectric materials. By defining a descriptor based on the experimental measurable and big data as an initial reference point, one can then utilise the descriptor to guide required computational accuracies and to quantify uncertainties for a given experimental condition. Thus, we suggest a descriptor based on the experimental measurable and big data as an initial reference point, and then utilise the descriptor to guide required computational accuracies and to quantify uncertainties for a given experimental condition. Figure 4 illustrates this scheme. Each microscopic quantity (Mi) can be calculated using the ab initio quantum mechanical simulation approaches. These theoretical approaches could range from ab initio DFT, time-dependent DFT and beyond-DFT approaches. There are many parameters (Ci) for each approach; viable Cis determine exchange-correlation functionals, pseudopotentials, basis sets, energy cutoff and so on. Beyond-DFT approaches require much more special attention on their performance depending on those Cis, because of their perturbative nature. Each microscopic quantity Mi can be presented in the configuration space of computational approaches,97 where each Ai is composed of a set of Cis. Those calculated values11 are connected to a materials property (Pi) through a descriptor (D(M)). Thus, one can quantify uncertainties of the microscopic quantities depending on computational parameters, and establish a property map with expected deviation.
Schematic for the workflow for a ‘materials by design’ approach. The description of the content in the dotted line is given in Figure 2.
For each microscopic parameter, one can perform benchmark calculations using, e.g., Quantum Monte Carlo for total energies and GW (an approximation made in order to calculate the self-energy of a many-body system of electrons) for the energy spectrum to establish a database. That database can enable quantification of the accuracy of the property map depending on computational parameters. Using machine learning, specifically a scalable Bayesian approach, we can further utilise the benchmark database for optimising ab initio parameters that maximise trustworthiness of theoretical predictions, and establish an optimised ab initio approach for a given system. The optimisation of an ab initio approach can be material specific or property specific. Once the uncertainty of each method is identified, trends can be categorised and used for the development and optimisation of theoretical approach.
One promising way is the construction of an accurate exchange-correlation functional is using machine learning.98 Until now, the approach is limited to the one-dimensional, non-interacting electrons and only applicable to system similar to the training (reference) data. This physics-inspired categorisation of big data can be excellent training data for the method where leadership computing is indispensable for the extension to three-dimensional, real material case. We note that optimisation of ab initio approaches can be material or property specific. Once the uncertainties of each method are identified, trends can be categorised and used for the development and optimisation of the theoretical approach. For example, the construction of an accurate exchange-correlation functional using machine learning.98 Overall, this approach can establish a tight feedback loop between first-principle calculations and experimental big-data analysis of microscopic and mesoscopic quantities. This will enable both verification of theoretical models and their improvement. It also allows validation of first-principle approaches and establishment of optimised theoretical approaches to enable predictive capabilities for materials by design.
Making the materials: enter the big data
The success of theoretical prediction of materials’ functionality has given rise to the paradigm of synthesis–measurement–computation in materials discovery/design. Here the rise of high-throughput computational capabilities99–103 has enabled massive parallel computations of materials functionality embodied in the Materials Genome Initiative, akin to the transition from individual artisanal fabrication to the production line in the beginning of twentieth century. However, exponential growth of the predictive computational capabilities is belied by the linear development of material synthesis pathways that still generally rely on the expertise and skills of the individual researcher and serendipity more than on the theory-driven prediction. In this regard, we note that broad incorporation of real-time process monitoring and data analytic and data mining tools can establish the correlations between preparation pathways and materials properties, potentially linking it to theoretical prediction and, in conjunction with artificial intelligence methods develop viable synthetic pathways. Although it is still a question whether this approach can create new knowledge, it will at least establish relevant correlations and summarise disjointed elements of phenomenological knowledge making it amenable for data mining and reuse.
From predicting to making
This approach can be illustrated by organic molecules, which have a long history of property prediction and successful synthesis, driven, e.g., by the need for new drugs. Indeed, computer programs to aid in the development of synthesis routes for relatively complex organic molecules goes back more than four decades, although the rational design of organic molecules certainly pre-dates this by several decades more. The sheer number of candidate molecules that can be synthesised increasingly necessitates these computer-aided designs. Early work focused on determining synthesis pathways given a bank of readily available compounds, as well as information on types of reactions present and their yields. These advances occurred at the same time as the birth of rational drug design,104 with numerous notable successes since.105–107 More recently, a strategy to account for synthesis complexity, i.e., ranking molecules based on the difficulty of synthesis has been proposed by Li and Eastgate.108,109 They propose a score termed the ‘current complexity’, which takes the available chemical synthesis methodology, and uses a computational method to determine the current complexity scores for different molecules. The score includes an intrinsic component based on the complexity of the structure of the organic molecule, as well as an extrinsic component based on the reaction and the synthetic scheme. As an example, the strychnine molecule current complexity was determined and showed clear reductions in complexity over several decades, reflecting the advances in synthesis techniques in the studied timeframe. Once a list of potential candidates is developed, subsequent ranking by these metrics will enable only the most viable molecules to be synthesised, greatly enhancing throughput. It should be noted that in the organic molecule case, the synthesis is generally carried out at constant temperature, constant pressure and is spatially uniform, in marked contrast to most inorganic materials with coupled functionalities that are of significant interest at present. These differences are illustrated in Figure 5, and highlight the progress that needs to be made.
(a) Organic molecules have one structure and are spatially uniform, to a first approximation. (b) For inorganic molecules, this is not the case, and, therefore, structure–property relations are more difficult to determine, as are synthetic pathways. Ball-stick model in a is the molecular structure of Cimetidine, from ref. 129.
Real-time analytics
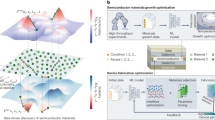
Incorporation of this approach for bulk inorganic materials is significantly more complex, as the process is now controlled by large number of spatially distributed parameters and can be strongly non-equilibrium. For example, we consider the case of pulsed laser deposition for the controlled growth of oxide nanostructures.110,111 Typically, the growth requires careful control over parameters including laser fluence, substrate temperature, background gas pressure and target composition in order to achieve the desired stoichiometry of the grown nanostructures (Figure 6). Other growth methods (e.g., molecular beam epitaxy or even single crystal growth) will require different control parameters, but nonetheless real-time monitoring of the process is always important for control over the desired compounds. An obvious drawback in pulsed laser deposition is that real-time feedback on chemical composition is not available, although new techniques involving in situ X-ray detectors112 and Auger electron spectroscopy113 are just beginning to emerge to fill this void. However, information pertaining to the dynamics of the growth of the structure through reflection high-energy electron diffraction is typically available, which is currently used to provide details on surface reconstructions, film morphology, film thickness and growth modes.114
For pulsed laser deposition (image above, left), typically the methodology is to tune control parameters based on optimising certain functional properties of the resulting sample, with little real-time feedback over surface morphology or chemical composition. This is largely due to difficulty in quantifying the real-time data, and inability to model the surface diffraction data in the dynamic growth process. Machine learning can bridge the existing gap between control parameters, real-time monitoring and functional properties of the grown material, as shown in the schema above, right.
Progress in this area requires bridging the gap between the parameters of the growth (which can be tuned), with the in situ monitoring of surface morphologies and chemical composition, along with the resulting functional properties of the grown material. By integrating this knowledge with real-time analytics of the diffraction or electron spectroscopy data, control over the resulting structures in terms of morphology115 and/or chemical composition should become possible. The big-data aspects are critical to this endeavour, given the multiple modalities of the captured data (and their large size), as well as the lack of appropriate quantitative theory to describe surface diffraction from high-energy electron diffraction geometries (or electron spectroscopies) during dynamic growth of oxide nanostructures. Overall, the full acquisition of data during the growth, along with correlation with the functional parameters of the resultant materials, will allow for data mining for properties that can be linked with the control variables, providing much greater flexibility, control and understanding of the dynamics of the growth process.
We further note that much of the experimental data, i.e., the link between the control parameters and the functional properties, already exists for, e.g., complex oxides,116,117 which have been studied for more than two decades. The challenge then is to mine the existing literature to find the growth conditions, and correlate them with the functional property. For ferroic thin films, this typically would involve determining film growth conditions (substrate temperature, laser fluence, background O2 pressure and so on) with the spontaneous polarisation PS, or the Curie temperature (or alternatively, the Néel temperature) through a careful text-based analysis of pulsed laser deposition papers on ferroic oxides. This will require developing the appropriate algorithms for text-based analysis of the several thousands of existing papers to look for the specific keyword–unit combinations (e.g., ‘fluence’ and ‘J/cm2), and compile them into an appropriate database that can subsequently be mined. Although each pulsed laser deposition chamber is different, presumably, given enough data trends can be identified for specific material compounds that can then be used to feed back into the synthesis. Future efforts must focus on developing the appropriate file format that can be used community-wide, possessing fields of the functional property of the oxide nanostructure, as well as the particular growth conditions, as well as metrics from real-time acquired spectroscopy/diffraction data, thereby negating the need for the text mining approach. The general schema is shown in Figure 7, with the aim of being able to build the hierarchical knowledge cluster from individual communities.
Although in practice these will differ in details, the overarching framework and best practices developed for the specific case in the section From predicting to making can be adopted.
Exploration of community-wide knowledge base
The immense investment in government-sponsored research in the United State has laid the foundation for national scientific, economic and military security in the twenty-first century. However, the doubling of scientific publication every 9 years118 jeopardises this foundation because it is no longer humanly possible to track relevant research. In order for scientists, to maintain awareness of relevant scientific work and continue advancements in fundamental and applied research requires development of new computational methods that effectively utilise newly emergent computational and machine learning capabilities for accelerating true scientific progress. Indeed, scientific discovery is generally driven by the synergy between talent, skills and inspiration of individual researchers. The character of research for the past century steadily shifted from individual effort (Tesla, Edison) in the beginning of twentieth century to small teams (Bardeen, Schokley and Schrieffer) to large multi-PI teams running complex and expensive instrumentation. Correspondingly, success of research is increasingly determined by the accessibility of corresponding equipment and collaborative infrastructure. The effectiveness of scientific research is often determined by the knowledge and experience of researcher, implying the knowledge base, social network of collaborators and capability to trace disjoined factors, find original references and meld these together. This will require the development of novel computational analytic capable of unlocking the human knowledge documented and archived in the unstructured text of hundreds of millions of scientific publications in order to extend scientific discovery beyond innate human capacity.
More specifically, there are two main challenges in using data analytics to aid scientific discovery; first, how to discover material within your field that may be overlooked due to the volume of information produced, and, second, how to find significant information within fields that you do not follow.
One approach to address these problems could be through the use of citation networks, pioneered by Chen27 through the Citespace program. This tool allows importation of a library of references on a particular topic (with full citations therein), and analyses the citation networks, which can then be clustered by keywords. Text-based analysis of the abstracts can reveal sudden changes in fields (through an entropy metric), whereas centrality of nodes defines the importance of a particular paper to a field in terms of connectedness to other clusters. As an example of the use of Citespace, the timeline in Figure 8 on the topic of BiFeO3 shows that the field experienced a resurgence in 2003 after the publication of the famous paper in Science by Wang et al.,119 on multiferroic BiFeO3 thin-film heterostructures. The same figure also reveals that there has been a considerable drop in interest over the past several years, presumably as attention has shifted to two-dimensional non-graphene materials or non-oxide ferroic compounds.
Citespace analysis of papers on BiFeO3. The size of the circle indicates the importance of the paper to the field, and the links between papers (through citations) are indicated by the arrows. Papers are plotted as circles in the year of publication. Papers are further organised into clusters, determined automatically by an algorithm based on keywords present. Figure made with Citespace.27
This concept can be progressed further via development of the advanced semantic analysis tools. For example, a set of author published papers can be used as seed documents to recommend documents of interest across various publication collections. This enables discovery of new sources that may be of interest, and refine the information within a source to only the most relevant. In order to process and analyse the large publications collections, each individual document is converted into a collection of terms and associated weights using the vector space model method. The vector space model is a widely recognised approach to document content representation120 in which the text in a document is characterised as a collection (vector) of unique terms/phrases and their corresponding normalised significance.
The weight associated with each unique term/phrase is the degree of significance that the term or phrase has, relative to the other terms/phrases. For example, if the term ‘metal’ is common across all or most documents, it will have a low significance, or weight value. Conversely, if ‘piezoelectric’ is a fairly unique term across the set of documents, it will have a higher weight value. The vector space model for any document is typically a combination of the unique term/phrase and its associated weight as defined by a term weighting scheme. Subsequently, the importance of the terms is weighted. Over the past three decades, numerous term weighting schemes have been proposed and compared121–125 with one of the most popular ones being frequency-inverse corpus frequency (TF-ICF) developed in ref 124. The primary advantage of using TF-ICF is the ability to process documents in O(N) time rather than O(N2) like many term weighting schemes, while also maintaining a high level of accuracy.
For convenience, the TF-ICF equation is provided here:
In this equation, fij represents the frequency of occurrence of a term j in document i. The variable N represents the total number of documents in the static corpus of documents, and nj represents the number of documents in which term j occurs in that static corpus. For a given frequency fij, the weight, wij, increases as the value of n decreases, and vice versa. Terms with a very high weight will have a high frequency fij, and a low value of n. This approach implemented in Piranha system (Figure 9) enables the discovery of publications outside a scientist’s field of interest, and the refinement of information within a scientist’s field.
Finally, even with targeted information that is relevant to the researcher, there is still the need to process, distil and summarise the available information quickly, and preferably, automatically. In fact, algorithms for the summarising of news articles online already exist.126 It is not inconceivable that in the future, writing of introduction sections (and other sections) of written papers will be largely computer aided. Indeed, papers written by computer algorithms127 are now believable enough that some have made it through to conference proceedings, despite consisting of gibberish.128 The key fact, however, is that they are grammatically correct, and given access to content aggregators, it is quite possible that much paper writing, e.g., of reviews, will be highly automated. These advances promise to increase the pace of materials design, while simultaneously allowing researchers to manage to keep abreast within increasingly complex, competitive and specialised topics.
Summary
In this perspective article, we have proposed bridging first-principle theoretical predictions and high-veracity imaging and scattering data of materials microscopic degrees of freedom through big-deep data, with the aim towards guided inorganic material synthesis. For the theoretical side, the overall goal is to provide a scalable, open-source and validated software framework, encompassing methods applicable to complex and correlated materials, which also incorporate error/uncertainty quantification for functional materials discovery/design. We argue that this can potentially be achieved by incorporation of the big-data approaches in imaging and scattering coupled with scalable first-principles software to enable large gains in the rate and quality of materials discoveries. By establishing a tight feedback loop between first-principle calculations and experimental big-data analysis of microscopic and mesoscopic quantities will enable both verification of theoretical models and their improvement. It also allows validation of first-principle approaches and establishment of optimised theoretical approaches.
With high-throughput computations in conjunction with high-veracity imaging and scattering data, the use of big-deep data will accelerate rational material design and synthesis pathways. A schema for the method, as applied to oxide films, is illustrated, incorporating real-time diffraction and chemical data from film growth linked with control parameters, synthesised and understood through deep learning. Additional challenges and opportunities in the realm of literature searches, citation analysis and advanced semantic analysis promise to speed up workflows for researchers, assist with paper production, and distil and categorise the existing scientific literature to enable targeted research, to enable better networking and to help researchers deal with the ever-increasing volume of data. Big data are making a quick and decisive entrance to the materials science community, and harnessing its potential will be critical for accelerated materials design and discovery to meet our current and future materials needs.
References
Riordan, M. & Hoddeson, L. Crystal Fire: The Invention of the Transistor and the Birth of the Information Age (W. W. Norton & Company, 1998).
Sze, S. M. Physics of Semiconductor Devices. 2nd edn (Wiley-Interscience, 1981).
Shockley, W. Electrons and Holes in Semiconductors: With Applications to Transistor Electronics (D. Van Nostrand Company, Inc., 1950).
Fuechsle, M. et al. A single-atom transistor. Nat. Nanotechnol. 7, 242–246 (2012).
Woodward, D. I., Knudsen, J. & Reaney, I. M. Review of crystal and domain structures in the PbZrxTi1-xO3 solid solution. Phys. Rev. B 72 104110 (2005).
Vugmeister, B. E. Polarization dynamics and formation of polar nanoregions in relaxor ferroelectrics. Phys. Rev. B 73 174117 (2006).
Binder, K. & Young, A. P. Spin-glasses - experimental facts, theoretical concepts, and open questions. Rev. Mod. Phys. 58, 801–976 (1986).
Dagotto, E. Complexity in strongly correlated electronic systems. Science 309, 257–262 (2005).
Dagotto, E., Hotta, T. & Moreo, A. Colossal magnetoresistant materials: The key role of phase separation. Phys. Rep. 344, 1–153 (2001).
Spaldin, N. A. & Fiebig, M. The renaissance of magnetoelectric multiferroics. Science 309, 391–392 (2005).
Adler, S. B. Factors governing oxygen reduction in solid oxide fuel cell cathodes. Chem. Rev. 104, 4791–4843 (2004).
Kalinin, S. V. & Spaldin, N. A. Functional ion defects in transition metal oxides. Science 341, 858–859 (2013).
Rao, CN, Sundaresan, A & Saha, R. Multiferroic and magnetoelectric oxides: the emerging scenario. J. Phys. Chem. Lett. 3, 2237–2246 (2012).
Hwang, H. Y., Iwasa, Y., Kawasaki, M., Keimer, B., Nagaosa, N. & Tokura, Y. Emergent phenomena at oxide interfaces. Nat. Mater. 11, 103–113 (2012).
Sando, D. et al. Crafting the magnonic and spintronic response of BiFeO3 films by epitaxial strain. Nat. Mater. 12, 641–646.
Allibe, J. et al. Room temperature electrical manipulation of giant magnetoresistance in spin valves exchange-biased with BiFeO3 . Nano. Lett. 12, 1141–1145 (2012).
Kruglyak, V. V., Demokritov, S. O. & Grundler, D. Magnonics. J. Phys. Appl. Phys. 43, 264001 (2010).
Holcomb, M. B. et al. Probing the evolution of antiferromagnetism in multiferroics. Phys. Rev. B 81, 134406 (2010).
Teague, J. R., Gerson, R. & James, W. J. Dielectric hysteresis in single crystal BiFeO 3. Solid State Commun. 8, 1073 (1970).
Michel, C., Moreau, J.-M., Achenbach, G. D., Gerson, R. & James, W. J.,. The atomic structure of BiFeO3 . Solid State Commun. 7, 701–704 (1969).
Catalan, G. & Scoot, J. F. Physics and applications of bismuth ferrite. Adv. Mater. 21, 2463 (2009).
Zeches, R. J. et al. A strain-driven morphotropic phase boundary in BiFeO3 . Science 326, 977 (2009).
Ohtomo, A., Muller, D. A., Grazul, J. L. & Hwang, H. Y. Artificial charge-modulationin atomic-scale perovskite titanate superlattices. Nature 419, 379–380 (2002).
Ohtomo, A. & Hwang, H. Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004).
Shibuya, K., Ohnishi, T., Kawasaki, M., Koinuma, H. & Lippmaa, M. Metallic LaTiO3/SrTiO3 superlattice films on the SrTiO3 (100) surface. Jpn J. Appl. Phys. 43, L1178–L1180 (2004).
Okamoto, S. & Millis, A. J. Electronic reconstruction at an interface between a Mott insulator and a band insulator. Nature 428, 630–633 (2004).
Chen, C. CiteSpaceII: detecting and visualizing emerging trends and transient patterns in scientific literature. J. Am. Soc. Inf. Sci. Technol. 57, 359–377 (2006).
Chen, C. Searching for intellectual turning points: Progressive knowledge domain visualization. Proc. Nat Acad. Sci. USA 101, 5303–5310 (2004).
Chen, C. Information Visualization: Beyond the Horizon (Springer Science & Business Media, 2006).
Chen, C. The Fitness of Information: Quantitative Assessments of Critical Evidence (John Wiley & Sons, 2014).
Materials Genome Initiative Strategic Plan. https://www.whitehouse.gov/sites/default/files/microsites/ostp/NSTC/mgi_strategic_plan_-_dec_2014.pdf
Ji, W., Yao, K. & Liang, Y. C. Bulk photovoltaic effect at visible wavelength in epitaxial ferroelectric BiFeO3 thin films. Adv. Mater. 22, 1763–1766 (2010).
Gygi, F. Qbox: a large-scale parallel implementation of First-Principles Molecular Dynamics (http://eslab.ucdavis.edu).
Payne, M. C., Teter, M. P., Allan, D. C., Arias, T. A. & Joannopoulos, J. D. Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients. Rev. Mod. Phys. 64, 1045–1097 (1992).
Soler, J. M. et al. The SIESTA method for ab initio order-N materials simulation. J. Phys. Cond. Matt. 14, 2745–2779 (2002).
Schmidt, M. W. et al. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 14, 1347–1363 (1993).
Valiev, M. et al. NWChem: a comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 181, 1477–1489 (2010).
Gaussian 09 (Gaussian, Inc., Wallingford, CT, USA, 2009).
Andersen, O. K. Linear methods in band theory. Phys. Rev. B 12, 3060 (1975).
Weinert, M., Wimmer, E. & Freeman, A. J. Total-energy all-electron density functional method for bulk solids and surfaces. Phys. Rev. B 26, 2571 (1982).
Williams, A. R., Kubler, J. & Gelatt, C. D. Cohesive properties of metallic compounds: augmented spherical-wave calculations. Phys. Rev. B 19, 6094 (1979).
Skriver, H. L. The LMTO Method (Springer-Verlag, 1984).
Eyert, V. The Augmented Spherical Wave Method (Springer, 2013).
Gonis, A. & Butler, W. H. Multiple Scattering in Solids (Springer, 2000).
Briggs, E. L., Sullivan, D. J. & Bernholc, J. Large-scale electronic-structure calculations with multigrid acceleration. Phys. Rev. B 52, R5471 (1995).
Bernholc, J., M. Hodak & Lu, W. Recent developments and applications of the real-space multigrid method. J. Phys. Condens. Matter 20, 294205.
Kronik, L. et al. PARSEC the pseudopotential algorithm for real-space electronic structure calculations: Recent Advances and novel applications to nano-structures. Phys. Stat. Sol. (b) 243, 1063–1079 (2006).
Enkovaara, J. et al. Electronic structure calculations with GPAW: a real-space implementation of the projector augmented-wave method. J. Phys.: Condens. Matter 22, 253202 (2010).
Eisenbach, M. et al. in SC09: Proceedings of the Conference of High Performance Computing, Networking, Storage and Analysis 1–64 (Association for Computing Machinery, 2009).
Eisenbach, M., Nicholson, D. M., Rusanu, A. & Brown, G. First principles calculations of finite temperature magnetism in Fe and Fe3C. J. Appl. Phys. 109, 07E138 (2011).
Fischer, C. C., Tibbetts, K. J., Morgan, D. & Ceder, G. Predicting crystal structure by merging data mining with quantum mechanics. Nat. Mater. 5, 641–646 (2006).
Curtarolo, S. et al. The high-throughput highway to computational materials design. Nat. Mater. 12, 191–201 (2013).
Montavon, G. et al. Machine learning of molecular electronic properties in chemical compound space. New J. Phys. 15, 095003 (2013).
Rupp, M., Tkatchenko, A., Müller, K.-R. & von Lilienfeld, O. A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 108, 058301 (2012).
Lopez-Bezanilla, A. & von Lilienfeld, O. A. Modeling electronic quantum transport with machine learning. Phys. Rev. B. 89, 235411 (2014).
Ramakrishnan, R., Dral, P. O., Rupp, M. & von Lilienfeld, O. A. Big data meets quantum chemistry approximations: the Δ-machine learning approach. J. Chem. Theory Comput. 11, 2087–2096 (2015).
Pyzer-Knapp, E. O., Suh, C., Gómez-Bombarelli, R., Aguilera-Iparraguirre, J. & Aspuru-Guzik, A. What Is high-throughput virtual screening? A perspective from organic materials discovery. Ann. Rev. Mater. Res. 45, 195–216 (2015).
Hachmann, J. et al. Lead candidates for high-performance organic photovoltaics from high-throughput quantum chemistry–the Harvard Clean Energy Project. Energy Environ. Sci. 7, 698–704 (2014).
Bartók, A. P., Gillan, M. J., Manby, F. R. & Csányi, G. Machine-learning approach for one-and two-body corrections to density functional theory: applications to molecular and condensed water. Phys. Rev. B. 88, 054104 (2013).
Elstner, M. et al. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 58, 7260–7268 (1998).
Seifert, G. & Joswig, J.-O. Density-functional tight binding-an approximate density-functional theory method. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2, 456 (2012).
Gaus, M., Cui, Q. & Elstner, M. Density functional tight binding: application to organic and biological molecules. Wiley Interdiscip. Rev. Comput. Mol. Sci. 4, 49 (2014).
Cui, Q. & Elstner, M. Density functional tight binding: values of semi-empirical methods in an ab initio era. Phys. Chem. Chem. Phys. 16, 14368–14377 (2014).
Zheng, G. et al. Implementation and benchmark tests of the DFTB method and its application in the ONIOM method. Int. J. Quantum Chem. 109, 1841 (2009).
Wang, Y., Qian, H.-J., Morokuma, K. & Irle, S. Coupled cluster and density functional theory calculations of atomic hydrogen chemisorption on pyrene and coronene as model systems for graphene hydrogenation. J. Phys. Chem. A 116, 7154–7160 (2012).
Walizer, L., Lisenkov, S. & Bellaiche, L. Finite-temperature properties of (Ba, Sr) Ti O3 systems from atomistic simulations. Phys. Rev. B 73, 144105 (2006).
Akbarzadeh, A. R., Prosandeev, S., Walter, E. J., Al-Barakaty, A. & Bellaiche, L. Finite-temperature properties of Ba(Zr, Ti)O3 relaxors from first principles. Phys. Rev. Lett. 108, 257601–257601 (2012).
Bellaiche, L., García, A. & Vanderbilt, D. Finite-temperature properties of Pb (Zr 1-x Ti x) O3 alloys from first principles. Phys. Rev. Lett. 84, 5427–5427 (2000).
Kornev, I. A., Bellaiche, L., Janolin, P.-E., Dkhil, B. & Suard, E. Phase diagram of Pb (Zr, Ti) O3 solid solutions from first principles. Phys. Rev. Lett. 97, 157601 (2006).
Bellaiche, L., Íñiguez, J., Cockayne, E. & Burton, B. P. Effects of vacancies on the properties of disordered ferroelectrics: A first-principles study. Phys. Rev. B 75, 014111 (2007).
Ponomareva, I., Naumov, I. I., Kornev, I., Fu, H. & Bellaiche, L. Atomistic treatment of depolarizing energy and field in ferroelectric nanostructures. Phys. Rev. B 72, 140102(R) (2005).
Ponomareva, I., Naumov, I. I. & Bellaiche, L. Low-dimensional ferroelectrics under different electrical and mechanical boundary conditions: atomistic simulations. Phys. Rev. B 72, 214118 (2005).
Noheda, B. et al. A monoclinic ferroelectric phase in the Pb (Zr1-x Tix) O3 solid solution. Appl. Phys. Lett. 74, 2059 (1999).
Kornev, I., Fu, H. & Bellaiche, L. Ultrathin films of ferroelectric solid solutions under a residual depolarizing field. Phys. Rev. Lett. 93, 196104 (2004).
Fong, D. D. et al. Ferroelectricity in ultrathin perovskite films. Science 304, 1650 (2004).
Naumov, I. I., Bellaiche, L. & Fu, H. Unusual phase transitions in ferroelectric nanodisks and nanorods. Nature 432, 737 (2004).
Lai, B.-K. et al. Electric-field-induced domain evolution in ferroelectric ultrathin films. Phys. Rev. Lett. 96, 137602 (2006).
Jia, C.-L., Urban, K. W., Alexe, M., Hesse, D. & Vrejoiu, I. Direct observation of continuous electric dipole rotation in flux-closure domains in ferroelectric Pb (Zr, Ti) O3 . Science 331, 1420 (2011).
Nelson, C. T. et al. Spontaneous vortex nanodomain arrays at ferroelectric heterointerfaces. Nano Lett. 11, 828 (2011).
Wang, D. et al. Fermi resonance involving nonlinear dynamical couplings in Pb (Zr, Ti) O3 solid solutions. Phys. Rev. Lett. 107, 175502 (2011).
Duane, S., Kennedy, A. D., Pendleton, B. J. & Roweth, D. Hybrid Monte Carlo. Phys. Lett. B 195, 216 (1987).
Kalinin, S. V., Sumpter, B. G. & Archibald, R. K. Big-deep-smart data in imaging for guiding materials design. Nat. Mater. 14, 973–980 (2015).
Crewe, A. V. Scanning electron microscopes - is high resolution possible. Science 154, 729–738 (1966).
Pennycook, S. J. & Nellist, P. D. (eds) Scanning Transmission Electron Microscopy Imaging and Analysis (Springer, New York, 2011).
Ardenne, M. V. Das elektronen-rastermikroskop. Praktische ausführung. Z. Tech. Phys. 19, 407–416 (1938).
Binnig, G., Rohrer, H., Gerber, C. & Weibel, E. 7X7 Reconstruction on SI(111) Resolved in real space. Phys. Rev. Lett. 50, 120–123 (1983).
Binnig, G. & Rohrer, H. Scanning tunneling microscopy. Helv. Phys. Acta 55, 726–735 (1982).
Pan, S. H. et al. Imaging the effects of individual zinc impurity atoms on superconductivity in Bi2Sr2CaCu2O8+delta. Nature 403, 746–750 (2000).
Roushan, P. et al. Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106–U1164 (2009).
Eigler, D. M. & Schweizer, E. K. Positioning single atoms with a scanning tunneling microscope. Nature 344, 524–526 (1990).
Lin, J. H. et al. Flexible metallic nanowires with self-adaptive contacts to semiconducting transition-metal dichalcogenide monolayers. Nat. Nanotechnol. 9, 436–442 (2014).
Pennycook, S. J., Zhou, W. & Pantelides, S. T. Watching Atoms Work: Nanocluster Structure and Dynamics. ACS Nano 9, 9437–9440 (2015).
Sohlberg, K., Rashkeev, S., Borisevich, A. Y., Pennycook, S. J. & Pantelides, S. T. Origin of anomalous Pt-Pt distances in the Pt/alumina catalytic system. ChemPhysChem 5, 1893–1897 (2004).
Kim, Y. M. et al. Probing oxygen vacancy concentration and homogeneity in solid-oxide fuel-cell cathode materials on the subunit-cell level. Nat. Mater. 11, 888–894 (2012).
Curtarolo, S., Morgan, D., Persson, K., Rodgers, J. & Ceder, G. Predicting crystal structures with data mining of quantum calculations. Phys. Rev. Lett. 91, 135503 (2003).
Yu, L. & Zunger, A. Identification of potential photovoltaic absorbers based on first-principles spectroscopic screening of materials. Phys. Rev. Lett. 108, 068701 (2012).
Baibich, M. N. et al. Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices. Phys. Rev. Lett. 61, 2472 (1988).
Snyder, J. C., Rupp, M., Hansen, K., Müller, K.-R. & Burke, K. Finding density functionals with machine learning. Phys. Rev. Lett. 108, 253002 (2012).
Materials Project. Available athttps://www.materialsproject.org.
Jain, A. et al. Commentary: The Materials Project: a materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
Jain, A. et al. A high-throughput infrastructure for density functional theory calculations. Comput. Mater. Sci. 50, 2295–2310 (2011).
Curtarolo, S. et al. AFLOWLIB.ORG: a distributed materials properties repository from high-throughput ab initio calculations. Comp. Mat. Sci. 58, 227–235 (2012).
Setyawan, W. & Curtarolo, S. High-throughput electronic band structure calculations: Challenges and tools. Comput. Mater. Sci. 49, 299–312 (2010).
Nogrady, T. & Weaver, D. F. Medicinal Chemistry: a Molecular and Biochemical Approach (Oxford Univ. Press, 2005).
Silverman, R. B. & Holladay, M. W. The organic Chemistry of Drug Design and Drug Action (Academic Press, 2014).
Wlodawer, A. & Vondrasek, J. Inhibitors of HIV-1 Protease: a major success of structure-assisted drug design 1. Ann. Rev. Biophys. Biomol. Struct. 27, 249–284 (1998).
Greer, J., Erickson, J. W., Baldwin, J. J. & Varney, M. D. Application of the three-dimensional structures of protein target molecules in structure-based drug design. J. Med. Chem. 37, 1035–1054 (Boston, 1994).
Li, J. & Eastgate, M. D. Current complexity: a tool for assessing the complexity of organic molecules. Org. Biomol. Chem. 13, 7164–7176 (2015).
Gasteiger, J. Cheminformatics: computing target complexity. Nat. Chem. 7, 619–620 (2015).
Eason, R. Pulsed Laser Deposition of Thin Films: Applications-Led Growth of Functional Materials (John Wiley & Sons, 2007).
Christen, H. M. & Eres, G. Recent advances in pulsed-laser deposition of complex oxides. J. Phys. Condens. Matter 20, 264005 (2008).
Neocera (ed Rama Vasudevan) (2014).
Staib, P. G. In situ real time Auger analyses during oxides and alloy growth using a new spectrometer design. J. Vac. Sci. Technol. 29, 03C125 (2011).
Ingle, N., Yuskauskas, A., Wicks, R., Paul, M. & Leung, S. The structural analysis possibilities of reflection high energy electron diffraction. J. Phys. D Appl. Phys. 43, 133001 (2010).
Vasudevan, R. K., Tselev, A., Baddorf, A. P. & Kalinin, S. V. Big-data reflection high energy electron diffraction analysis for understanding epitaxial film growth processes. ACS Nano 8, 10899–10908 (2014).
Mannhart, J. & Schlom, D. Oxide interfaces—an opportunity for electronics. Science 327, 1607–1611 (2010).
Ramesh, R. & Spaldin, N. A. Multiferroics: progress and prospects in thin films. Nat. Mater. 6, 21–29 (2007).
Bornmann, L. & Mutz, R. Growth rates of modern science: a bibliometric analysis based on the number of publications and cited references. J. Assoc. Inf. Sci. Technol. 66, 2215–2222 (2015).
Wang, J. et al. Epitaxial BiFeO3 multiferroic thin film heterostructures. Science 299, 1719–1722 (2003).
Pinheiro, W. et al. in ICAS'09. Fifth International Conference on Autonomic and Autonomous Systems. 148–153 (IEEE, 2009).
Burkepile, A. & Fizzano, P. in Second International Conference on Information, Process, and Knowledge Management 43–47 (IEEE, 2010).
Chapelle, O., Schölkopf, B. & Zien, A. Semi-Supervised Learning (The MIT Press, Cambridge, MA, USA, 2006).
Porter, M. F. An algorithm for suffix stripping. Program 14, 130–137 (1980).
Reed, J. W. et al. in ICMLA '06. 5th International Conference on Machine Learning and Applications. 258–263 (IEEE, 2006).
Patton, R. M., Potok, T. E. & Worley, B. A. in The Second International Conference on Advanced Communications and Computation 1–5 (IARIA).
Barzilay, R. & McKeown, K. R. Sentence fusion for multidocument news summarization. Comput. Ling. 31, 297–328 (2005).
Stribling, J., Krohn, M. & Aguayo, D. Scigen-an automatic cs paper generator. Available at http://pdos.csail.mit.edu/scigen (2005).
Publishers withdraw more than 120 gibberish papers Nature (2014) Available at http://www.nature.com/news/publishers-withdraw-more-than-120-gibberish-papers-1.14763.
Cernik, R. et al. The structure of cimetidine (C10H16N6S) solved from synchrotron-radiation X-ray powder diffraction data. J. Appl. Crystallogr. 24, 222–226 (1991).
Acknowledgements
Research was conducted at the Center for Nanophase Materials Sciences, which is a DOE Office of Science User Facility. This research was sponsored by the Division of Materials Sciences and Engineering, BES, DOE (RKV and SVK). The authors acknowledge useful discussion and figures provided by Mina Yoon.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sumpter, B., Vasudevan, R., Potok, T. et al. A bridge for accelerating materials by design. npj Comput Mater 1, 15008 (2015). https://doi.org/10.1038/npjcompumats.2015.8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/npjcompumats.2015.8
This article is cited by
-
Dataset of solution-based inorganic materials synthesis procedures extracted from the scientific literature
Scientific Data (2022)
-
An infrastructure with user-centered presentation data model for integrated management of materials data and services
npj Computational Materials (2021)
-
Accelerated design and characterization of non-uniform cellular materials via a machine-learning based framework
npj Computational Materials (2020)
-
Phase-field modeling and machine learning of electric-thermal-mechanical breakdown of polymer-based dielectrics
Nature Communications (2019)
-
Identification of stable adsorption sites and diffusion paths on nanocluster surfaces: an automated scanning algorithm
npj Computational Materials (2019)