Abstract
Superconductivity can be induced in a normal material via the ‘leakage’ of superconducting pairs of charge carriers from an adjacent superconductor. This so-called proximity effect is markedly influenced by graphene’s unique electronic structure, both in fundamental and technologically relevant ways. These include an unconventional form1,2 of the ‘leakage’ mechanism—the Andreev reflection3—and the potential of supercurrent modulation through electrical gating4. Despite the interest of high-temperature superconductors in that context5,6, realizations have been exclusively based on low-temperature ones. Here we demonstrate a gate-tunable, high-temperature superconducting proximity effect in graphene. Notably, gating effects result from the perfect transmission of superconducting pairs across an energy barrier—a form of Klein tunnelling7,8, up to now observed only for non-superconducting carriers9,10—and quantum interferences controlled by graphene doping. Interestingly, we find that this type of interference becomes dominant without the need of ultraclean graphene, in stark contrast to the case of low-temperature superconductors11. These results pave the way to a new class of tunable, high-temperature Josephson devices based on large-scale graphene.
Similar content being viewed by others
Main
Superconductivity is induced in a normal metal (N) in contact with a superconductor (S) via the Andreev reflection (AR)3: an electron entering S from N pairs to another electron to form a Cooper pair, leaving a hole-like quasiparticle that is transmitted back into N. Electron and hole coherently propagate with parallel opposite wavevectors, carrying superconducting correlations into N. This mechanism allows supercurrent flow and Josephson coupling across S–N–S junctions12.
S–N proximity devices that can be greatly tuned by electrostatic doping are one of the main technological prospects of induced superconductivity in graphene4,13,14,15,16. Several specific mechanisms allow for that. Besides the density-of-states narrowing at the Dirac point, around which the junction’s resistance increases, subtler effects may play a role. For example, the unusual possibility that the AR-involved electron and hole reside in different bands—conduction and valence—results in a specular Andreev reflection1 (SAR) in which electron and hole wavevectors are mirror-like. SAR can occur if the graphene’s Fermi energy EF is lower than the superconducting energy gap Δ, while for EF > Δ the conventional (intra-band) AR takes place1. Thus, an AR to SAR crossover can be driven by shifting EF through a gate voltage, which dramatically changes the S–N interface conductance2.
In the present experiments, tunability results from a different mechanism that involves Klein tunnelling—that is, the reflectionless transmission of electrons across a high energy barrier7,8,9,10. Beyond single electrons, here we observe Klein-like tunnelling of Andreev electron–hole pairs that carry superconducting correlations from the high-temperature superconductor YBa2Cu3O7 (YBCO) into graphene. That effect is associated with quantum interferences across the barrier, which modulate the overall penetration of superconducting pairs into graphene. Those interferences are gate-tunable because the wavevector of graphene’s massless charge carriers is proportional to EF. Although extremely sensitive to EF inhomogeneities comparable to Δ—which has confined their pristine observation to ultraclean exfoliated graphene11—we find that the large Δ of YBCO makes interference effects robust in chemical vapour deposited (CVD) graphene. This increases the technological potential of the observed effects.
Fabricating YBCO/graphene devices with electron-transparent interfaces has remained challenging17. Contrary to low-temperature superconductors2,4,11,13,14,15,16,18,19,20, YBCO cannot be grown on graphene due to its deposition conditions (hundreds of °C, oxygen-rich atmosphere). Conversely, the surface electronic properties of YBCO are easily degraded by standard graphene fabrication and lithography techniques. To circumvent those constraints, we used 50-nm-thick YBCO films grown on SrTiO3 (STO) and covered in situ with an ultrathin 4 nm Au layer. This protects the YBCO surface and constitutes a high-transparency interface with graphene. Then we applied a masked ion irradiation technique (details in Fig. 1) that allowed us to fabricate planar devices as shown in Fig. 1e: four superconducting YBCO/Au electrodes (bright colour) defined within an insulating YBCO matrix (dark colour) are bridged by an overlaying single-layer CVD graphene sheet. With this device, we study the YBCO/Au/graphene junction conductance using a three-probe configuration, with the current I injected between electrodes 1 and 4 and the voltage V measured between 3 and 4 (sketch in Fig. 1e). In that configuration the contributions of the YBCO leads and the YBCO/Au interface to the measured conductance are negligible (see Supplementary Section 1). Thus, the measurement allows us to probe the Au/graphene conductance and, particularly, the proximity behaviour of that single interface. Notice also that the ultrathin Au layer is expected to sustain proximity-induced d-wave superconductivity (see Supplementary Section 1). We stress that here we do not investigate the Josephson effect across graphene, which is neither observed nor expected because the distance between YBCO/Au electrodes (∼5 μm) is much larger than the estimated coherence length in graphene  nm at 4 K. Back-gating through the dielectric STO substrate (scheme in Fig. 2c) is used to investigate the effects of doping graphene on the proximity behaviour.
nm at 4 K. Back-gating through the dielectric STO substrate (scheme in Fig. 2c) is used to investigate the effects of doping graphene on the proximity behaviour.
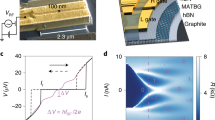
a, Starting with an Au (4 nm)/YBCO (50 nm) film grown on SrTiO3, photolithography is used to define a resist pattern through which the film is irradiated with 110 KeV O+ ions at high fluence (5 × 1014 cm−2). This turns the unprotected YBCO electrically insulating. Conversely, the resist-covered YBCO maintains superconducting (S) properties. b, After subsequently removing Au (via Ar+ ion etching) and the resist mask, a planar device is obtained with S electrodes (bright colour) defined within an insulating YBCO matrix (dark). A CVD single-layer graphene sheet is then transferred as reported elsewhere26. c, Graphene is patterned using photolithography and oxygen plasma to obtain a channel that bridges the S electrodes. d, Sketch of the final device. e, Microscope image of an actual device. The graphene layer has been outlined (red-dashed line) for clarity. In green, a sketch of the measurement geometry.
a, Differential conductance of the YBCO/Au/graphene junction in zero applied field and different temperatures (in K). b, Normalized conductance at zero magnetic field and T = 4 K for two gate voltages: VG = 0 V (top) and VG = −40 V (bottom). c, Scheme of the device cross-section. Graphene, in grey, is superconducting (S) above the superconducting YBCO (light colour), and normal (N′ and N) elsewhere. The insulating (Ins) YBCO is depicted in dark colour. The boundary between superconducting and insulating YBCO has a width of a few tens of nanometres (graded colour). Gating is achieved across the dielectric STO substrate.
Figure 2a shows the differential conductance G = dI/dV versus V at several temperatures T in zero applied magnetic field. For T well above the critical temperature TC ∼ 80 K, the V dependence is relatively weak and G decreases with increasing |V|. Upon decreasing T below TC, a large conductance enhancement develops around zero bias, accompanied by two dips near ±20 mV. Those features become more pronounced as T decreases. At the lowest T, the zero-bias conductance is nearly twice the conductance at V = 60 mV (this is well above the YBCO superconducting gap21). Magnetic fields up to H = 6 kOe had no effect on G(V) (data not shown). In contrast, G(V) is strongly modulated by back-gating.
Following the scheme in Fig. 2c, the application of a gate voltage VG leads to graphene doping due to the polarization of the substrate (STO) and the irradiated (insulating) YBCO. Fig. 2b illustrates the effects of VG. For convenience, the normalized conductance g(V) ≡ G(V)/GN(V) is shown, with GN(V) the normal-state one at 120 K. The conductance under VG = −40 V (bottom panel) is markedly different from that for VG = 0 V (top panel): changes in the zero-bias peak width and height, in the dips’ depth and in the conductance background are observed. Notice, for example, a conductance enhancement (g > 1) for VG = −40 V (bottom) within the bias range in which dips and g < 1 are observed for VG = 0 V (top). As discussed below, the curves in Fig. 2b constitute two behaviour types between which g(V) periodically switches as a function of VG.
Figure 3a displays g(V, VG) in a contour plot generated from a series of measurements such as those in Fig. 2b (data range is |V| < 30 mV (around 1.5Δ) and |VG| < 100 V in this figure; the data for the whole experimental window is displayed in Supplementary Fig. 6). The zero-bias peak observed for all VG (Fig. 2b) appears in the contour plot as a vertical ‘band’ (in red). The conductance dips observed around ±∼20 mV in Fig. 2b show up in the plot as ‘pockets’ (in purple colour). The background enhancement (g > 1) seen in Fig. 2b for VG = −40 V and |V| < 40 mV is shown in the plot as a horizontal feature (in green). Purple ‘pockets’ and green horizontal features alternate periodically along the y-axis—that is, as a function of VG. This periodic modulation is highlighted in Fig. 3b, which displays g(VG) for fixed V —this corresponds to vertical ‘cuts’ of the contour plot, marked with the dashed lines Θ and Σ in Fig. 3a. Notice (Fig. 3b) that the periodic modulation is accompanied by a conductance background decrease for increasing VG. Further analysis of the oscillatory behaviour can be found in Supplementary Fig. 7.
a, Contour plot of the normalized conductance (colour scale) as a function of junction bias V and gate voltage VG. This plot is constructed from a series of measurements as those shown in Fig. 2, with ΔVG = 20 V. b, Experimental conductance as a function of gate voltage VG at fixed bias V, which correspond to vertical ‘cuts’ of the plot in a along the dashed lines labelled Θ and Σ (respectively for V = 0 ± 1 mV and V = 20 ± 1 mV). Various points per VG exists which denote the measurement uncertainty (see Supplementary Section 7 for further details). The solid line behind the data is a guide to the eye. c, Experimental conductance versus bias V for fixed gate voltages VG. Each panel corresponds to a horizontal ‘cut’ of the plot in a along the lines labelled A, B, C, D (respectively for VG = 60, 40, 0 and −100 V). The arrow points to the conductance dip below eV = Δ. d–f, Numerical simulations corresponding to the measurements in a–c. Notice that in the simulation the bias V is normalized by the superconducting gap Δ, and the experimental quantity VG is replaced by the phase χ. g, Schematic of the theoretical model. A potential step of width w and height U0 defines a region of normal graphene (N′) that separates superconducting graphene with Fermi energy EF′ from normal graphene (N) with gate-tunable Fermi energy EF(VG).
To interpret the experimental results, we start by considering the conductance across generic superconductor/normal (S/N) interfaces22. In this context, the zero-bias conductance doubling at low T (Fig. 2a) suggests a highly transparent S/N interface governed by AR22 (devices showing reduced transparency are discussed in Supplementary Section 2). The invariance of the conductance curves with respect to the magnetic field is consistent with that scenario. VG effects imply that graphene is necessarily the ‘N’ part of the S/N junction, and rule out a possible role of the YBCO/Au interface23. This is because the device geometry ensures that VG solely affects graphene that lies on insulating YBCO (dark in Fig. 2c). The electric field is fully screened elsewhere by the superconducting YBCO (bright in Fig. 2c), whose properties are unaffected by VG because its thickness is ∼50 times the Thomas–Fermi screening length24.
The overall experimental details are explained by the model sketched in Fig. 3g. This model is based on the expectation that graphene on top of superconducting YBCO/Au becomes superconducting (S) due to the proximity effect1 and presents a fixed doping EF′, while graphene on top of insulating YBCO is normal (N) and presents a gate-tunable doping EF(VG). Then we assume that there is an intermediate region N′ of width w in which graphene is normal but presents different doping than in S and N (see Supplementary Section 5). This scenario leads to a potential energy step U0 for electrons at the boundary between S and N graphene6 (note that replacing S by normal graphene (N) results in a type of graphene N–N′–N junction in which regular—non-superconducting—Klein tunnelling is expected7,8,9,10). The conductance across such an S–N′–N junction has been theoretically studied both for s-wave5,6,25 and d-wave superconductors5,6 (note that in those works exactly the same junction structure was referred to as S–I–N). The central effect arises due to interferences of electrons and holes travelling from the N′–N to the S–N′ interface (and vice versa after reflection at the S–N′ interface). Depending on the phase χ = −wkF picked up by electrons/holes across N′ (with kF the Fermi vector), constructive or destructive interference occurs, which periodically modulates the junction conductance as a function of χ6. Thus, due to graphene’s linear dispersion, χ = w(EF − U0)/ℏvF (with vF the Fermi velocity) and a periodic conductance modulation as a function of EF is expected. That can explain the gating effects observed in Fig. 3a, b. To support this, we used the existing theory6 to perform the numerical simulations shown in Fig. 3d–f.
Simulations of g(eV /Δ, χ) require several input parameters: the native Fermi energy in N, EF(0); the Fermi energy in S, EF′; the proportionality factor between EF variation and phase shift δEF/δχ; and the angle α between the d-wave nodes and the S–N′ interface5. As discussed in Supplementary Section 4, most of these parameters are known from independent experiments, and only α and EF′ remain as fitting parameters. Figure 3d shows the best agreement between theory and experiments, obtained for α = π/4,EF′ = 20Δ, EF(0) = 17.5Δ, and δEF/δχ = 5Δ/3π. Notably, all of the characteristic features seen in the experimental g(V, VG) (Fig. 3a) can be found in Fig. 3d: a vertical band (in red) that corresponds to a zero-bias conductance peak due to AR, and a periodic modulation along the y-axis in which horizontal features due to enhanced conductance (in green) alternate with ‘pockets’ (in purple). Figure 3e shows vertical ‘cuts’ of the theoretical plot along the lines Θ and Σ, which closely mimic the experimental ones (Fig. 3b). ‘Cuts’ along the x-axis (labelled A, B, C, D) are also shown for experiments and theory, respectively, in Fig. 3c, f. Their comparison show that the simulations not only successfully reproduce the periodic gating effects, but also the essential details of the experimental g(V): a conductance enhancement around zero bias, ‘dips’ around eV ∼ Δ, and the evolution of these features with VG (phase χ). The overall agreement between simulation and experiment demonstrates that the used model6 captures the physics of the studied system. Further improving the match between theory and experiment, particularly for eV > ∼ 1.5Δ where discrepancies appear (see Supplementary Fig. 6), may require refining the model, for example, by considering different barrier profiles (for example, trapezoidal instead of square), smeared or rough S/N′/N interfaces, and so on (see discussion in Supplementary Section 5). We hope that the present experiments will motivate that work.
In summary, the periodic modulation of the conductance is explained by electron interferences within an energy barrier that separates normal and superconducting graphene. The barrier is essentially transparent to electron/hole superconducting pairs (as well as for normal electrons) when the phase picked across the barrier is χ = nπ, which corresponds to Klein tunnelling of superconducting pairs. Thus, the interferences allow for an electrostatic tuning of the superconducting proximity effect, since the fraction of the current carried by electron–hole superconducting pairs (created by AR) is modulated by χ(VG) (ref. 6). These results open interesting perspectives. For instance, experiments aimed at selecting the pairing symmetry induced in graphene via the control of the orientation of the graphene and YBCO lattices26, gate-tunable high-temperature Josephson devices using large-scale—not necessarily ultraclean—graphene, and possibly more elaborate devices in which those effects, the salient features of d-wave superconductivity and the directional nature of Klein tunnelling7 may be exploited together, for example, to create tunable ‘pi’ Josephson junctions27.
Note added in proof: During the resubmission of the paper we learnt about the publication of related scanning tunnelling microscopy experiments of graphene on a different cuprate superconductor28.
Methods
c-axis YBCO thin films (50 nm thick) were grown on (100) SrTiO3 (STO) substrates (500 μm thick) by pulsed-laser deposition at 700 °C and 0.35 mbar of pure oxygen. The optimum oxygen stoichiometry is ensured by cooling down to room temperature in 800 mbar of pure oxygen. Subsequently the chamber base pressure (3 × 10−6 torr) is reinstated, and an ultrathin Au film (∼4 nm thick) is deposited in situ on top of the YBCO to protect its surface. YBCO c-axis epitaxial growth is confirmed by reflection high-energy electron diffraction (in situ) and X-ray diffraction (ex situ), and film thicknesses are determined by X-ray reflectivity. Atomic force microscopy of the Au/YBCO bilayer shows flat surfaces with typical r.m.s. roughness ∼3 nm.
Graphene transfer onto the lithographed devices was done as reported elsewhere29.
Electrical characterization within the 3 K–300 K range was carried in a He-flow cryostat equipped with a 6kOe electromagnet. In the three-probe configuration, the current is injected between contacts 1 and 4, and the voltage probes are attached to contacts 3 and 4 (see image in Fig. 1e). dI/dV (V) is obtained using the current-biased Keithley delta mode with a coupled K2182 nanovoltmeter and K6221 current source.
Data availability.
The data supporting the plots within this paper and other findings of this study are available from the corresponding author on reasonable request.
Additional Information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Beenakker, C. W. J. Specular Andreev reflection in graphene. Phys. Rev. Lett. 97, 67007 (2006).
Efetov, D. K. et al. Specular interband Andreev reflections at van der Waals interfaces between graphene and NbSe2 . Nat. Phys. 12, 328–332 (2015).
Andreev, A. F. The thermal conductivity of the intermediate state in superconductors. Sov. Phys. JETP 19, 1228–1231 (1964).
Heersche, H. B., Jarillo-Herrero, P., Oostinga, J. B., Vandersypen, L. M. K. & Morpurgo, A. F. Bipolar supercurrent in graphene. Nature 446, 56–59 (2007).
Linder, J. & Sudbø, A. Dirac fermions and conductance oscillations in s- and d-wave superconductor-graphene junctions. Phys. Rev. Lett. 99, 147001 (2007).
Linder, J. & Sudbø, A. Tunneling conductance in s- and d-wave superconductor-graphene junctions: extended Blonder–Tinkham–Klapwijk formalism. Phys. Rev. B 77, 64507 (2008).
Katsnelson, M., Novoselov, K. & Geim, A. Chiral tunnelling and the Klein paradox in graphene. Nat. Phys. 2, 620–625 (2006).
Beenakker, C. W. J. Colloquium: Andreev reflection and Klein tunneling in graphene. Rev. Mod. Phys. 80, 1337–1354 (2008).
Huard, B. et al. Transport measurements across a tunable potential barrier in graphene. Phys. Rev. Lett. 98, 236803 (2007).
Young, A. F. & Kim, P. Quantum interference and Klein tunnelling in graphene heterojunctions. Nat. Phys. 5, 222–226 (2009).
Ben Shalom, M. et al. Quantum oscillations of the critical current and high-field superconducting proximity in ballistic graphene. Nat. Phys. 12, 318–322 (2015).
Klapwijk, T. M. Proximity effect from an Andreev perspective. J. Supercond. 17, 593–611 (2004).
Du, X., Skachko, I. & Andrei, E. Y. Josephson current and multiple Andreev reflections in graphene SNS junctions. Phys. Rev. B 77, 184507 (2008).
Ojeda-Aristizabal, C., Ferrier, M., Guéron, S. & Bouchiat, H. Tuning the proximity effect in a superconductor–graphene–superconductor junction. Phys. Rev. B 79, 165436 (2009).
Girit, Ç. et al. Tunable graphene dc superconducting quantum interference device. Nano Lett. 9, 198–199 (2009).
Komatsu, K., Li, C., Autier-Laurent, S., Bouchiat, H. & Guéron, S. Superconducting proximity effect in long superconductor/graphene/superconductor junctions: from specular Andreev reflection at zero field to the quantum Hall regime. Phys. Rev. B 86, 115412 (2012).
Sun, Q. J. et al. Electronic transport transition at graphene/YBa2Cu3O7-δ junction. Appl. Phys. Lett. 104, 102602 (2014).
Rickhaus, P., Weiss, M., Marot, L. & Schönenberger, C. Quantum Hall effect in graphene with superconducting electrodes. Nano Lett. 12, 1942–1945 (2012).
Deon, F., Šopić, S. & Morpurgo, A. F. Tuning the influence of microscopic decoherence on the superconducting proximity effect in a graphene Andreev interferometer. Phys. Rev. Lett. 112, 126803 (2013).
Allen, M. T. et al. Spatially resolved edge currents and guided-wave electronic states in graphene. Nat. Phys. 12, 128–133 (2016).
Wei, J. Y. T., Yeh, N.-C., Garrigus, D. F. & Strasik, M. Directional tunneling and Andreev reflection on YBa2Cu3O7−δ single crystals: predominance of d-wave pairing symmetry verified with the generalized Blonder, Tinkham, and Klapwijk theory. Phys. Rev. Lett. 81, 2542–2545 (1998).
Blonder, G. E., Tinkham, M. & Klapwijk, T. M. Transition from metallic to tunneling regimes in superconducting micro-constrictions—excess current, charge imbalance, and super-current conversion. Phys. Rev. B 25, 4515–4532 (1982).
Kashiwaya, S., Tanaka, Y., Koyanagi, M., Takashima, H. & Kajimura, K. Origin of zero-bias conductance peaks in high-Tc superconductors. Phys. Rev. B 51, 1350–1353 (1995).
Crassous, A. et al. Nanoscale electrostatic manipulation of magnetic flux quanta in ferroelectric/superconductor BiFeO3/YBa2Cu3O7−δ heterostructures. Phys. Rev. Lett. 107, 247002 (2011).
Bhattacharjee, S. & Sengupta, K. Tunneling conductance of graphene NIS junctions. Phys. Rev. Lett. 97, 217001 (2006).
Linder, J., Black-Schaffer, A. M., Yokoyama, T., Doniach, S. & Sudbø, A. Josephson current in graphene: role of unconventional pairing symmetries. Phys. Rev. B 80, 94522 (2009).
Cedergren, K. et al. Interplay between static and dynamic properties of semifluxons in YBa2Cu3O7−δ 0-π Josephson junctions. Phys. Rev. Lett. 104, 177003 (2010).
Bernard, A. Di et al. p-wave triggered superconductivity in single-layer graphene on an electron-doped oxide superconductor. Nat. Commun. 8, 14024 (2017).
Kidambi, P. R. et al. The parameter space of graphene CVD on polycrystalline Cu. J. Phys. Chem. C 116, 22492–22501 (2012).
Acknowledgements
Work at CNRS/Thales was supported by the French National Research Agency through ‘Investissements d’Avenir’ program Labex NanoSaclay (ANR-10-LABX-0035) and by the EU Work Programme under Grant Graphene Flagship (No. 604391) and Core1 (No. 696656). R.G. acknowledges funding from the Marie-Curie-ITN 607904-SPINOGRAPH. S.H. acknowledges funding from EPSRC grants EP/K016636/1 and EP/P005152/1. P.S. acknowledges the Institut Universitaire de France for a junior fellowship. We thank A. S. Mel’Nikov, J. Linder, J. Santamaría, S. Gueron and H. Bouchiat for useful discussions. We thank Y. Le Gall for assistance during ion irradiation.
Author information
Authors and Affiliations
Contributions
J.E.V. and P.S. conceived the experiments. R.B. fabricated the YBCO films. P.R.K., M.-B.M. and S.H. fabricated the graphene sheets. F.A.C., fabricated the devices, with contributions from D.P., B.D., R.G. and M.P.-B. F.A.C. performed transport experiments, with contributions of D.P. and C.M.-L. D.P. performed numerical simulations. The figures were prepared and the paper written by D.P., F.A.C. and J.E.V., with contributions from all the other authors. All of the authors participated in the discussion of the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1722 kb)
Rights and permissions
About this article
Cite this article
Perconte, D., Cuellar, F., Moreau-Luchaire, C. et al. Tunable Klein-like tunnelling of high-temperature superconducting pairs into graphene. Nature Phys 14, 25–29 (2018). https://doi.org/10.1038/nphys4278
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys4278
This article is cited by
-
Observation of interaction-induced phenomena of relativistic quantum mechanics
Communications Physics (2021)
-
Unconventional superconductivity in magic-angle graphene superlattices
Nature (2018)