Abstract
The generation, manipulation and detection of spin-polarized electrons in low-dimensional semiconductors are at the heart of spintronics. Pure spin currents, that is, fluxes of magnetization without charge current, are quite attractive in this respect. A paradigmatic example is the spin Hall effect, where an electrical current drives a transverse spin current and causes a non-equilibrium spin accumulation observed near the sample boundary1,2. Here we provide evidence for an another effect causing spin currents which is fundamentally different from the spin Hall effect. In contrast to the spin Hall effect, it does not require an electric current to flow: without bias the spin separation is achieved by spin-dependent scattering of electrons in media with suitable symmetry. We show, by free-carrier absorption of terahertz (THz) radiation, that spin currents flow in a wide range of temperatures. Moreover, the experimental results provide evidence that simple electron gas heating by any means is already sufficient to yield spin separation due to spin-dependent energy-relaxation processes.
Similar content being viewed by others
Main
Scattering of electrons involves a transition from a state with wavevector k to a state with wavevector k′ which is usually considered to be spin-independent. However, in gyrotropic media, for example, GaAs quantum wells (QWs) or heterojunctions, spin–orbit interaction adds an asymmetric spin-dependent term to the scattering probability. The asymmetric spin-dependent scattering matrix element is linear in wavevector k and the Pauli spin matrices σ (note, that in fact all terms odd in k, including k-cubic terms, may also contribute to spin-dependent asymmetric scattering). Microscopically, this term is caused by structural inversion asymmetry (SIA) and/or bulk inversion asymmetry. Although the asymmetry of electron scattering can cause spin currents to flow, it does not modify the energy spectrum.
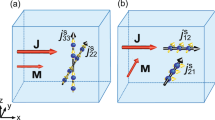
A process actuating spin separation is illustrated in Fig. 1a and involves Drude absorption of radiation. Drude absorption is caused by indirect intraband optical transitions and includes a momentum transfer from phonons or impurities to electrons to satisfy momentum conservation. Figure 1a shows the process of Drude absorption via virtual states for a spin-up subband (s=+1/2, left panel) and a spin-down subband (s=−1/2, right panel) of a QW containing a two-dimensional electron gas (2DEG). Vertical arrows indicate optical transitions from the initial state kx=0, whereas the horizontal arrows describe an elastic scattering event to a final state with either positive or negative electron wavevector k′x. Although, for simplicity, we have only drawn transitions starting from kx=0, the argument holds for arbitrary kx. Owing to the spin dependence of scattering, transitions to positive and negative k′x states occur with different probabilities. This is indicated by horizontal arrows of different thickness. As the asymmetric part of electron scattering is proportional to components of [σ×k′], probabilities for scattering to positive or negative k′x are inverted for spin-down and spin-up subbands (note that we assumed kx=0, and the presence of SIA alone). Similarly, relaxation of excited carriers is also asymmetric as is shown in Fig. 1b. As the latter mechanism only causes a polarization-independent background signal in the experiments discussed below, the discussion will first focus on the mechanism shown in Fig. 1a.
To illustrate the model we draw spin-up and spin-down subbands of the conduction band separately. a,b, Scattering matrix elements linear in k and σ cause asymmetric scattering for both excitation via Drude absorption (a) and relaxation (b). Here, scattering for the spin-up subband is assumed to have a larger probability for positive kx than that for negative kx and vice versa for the spin-down subband.
The asymmetry causes an imbalance in the distribution of photoexcited carriers for s=±1/2 subbands between positive and negative k′x states. This in turn yields electron flows i±1/2 within each spin subband3. However, the charge currents, j+=e i1/2 and j−=e i−1/2, where e is the electron charge, have opposite directions because i+1/2=−i−1/2 and therefore cancel each other. Nevertheless, a spin current Jspin=(1/2)(i+1/2−i−1/2) is generated because electrons with spin-up and spin-down move in opposite directions. This leads to a spatial spin separation and spin accumulation at the edges of the sample.
By applying a magnetic field that polarizes spins, the spin current is detected as charge current. In a spin-polarized system, the two fluxes i±1/2, which are proportional to the spin-up and spin-down free carrier densities, n±1/2, cease compensating each other and yield a net electric current

where S=(1/2)(n+1/2−n−1/2)/(n+1/2+n−1/2) is the magnitude of the average spin. An external magnetic field, B, results in different populations of the two spin subbands due to the Zeeman effect. In equilibrium, the average spin is given by

Here g is the electron effective g factor, μB is the Bohr magneton,  is the characteristic electron energy being equal to the Fermi energy ɛF, or to the thermal energy kBT, for a degenerate or a non-degenerate 2DEG, respectively.
is the characteristic electron energy being equal to the Fermi energy ɛF, or to the thermal energy kBT, for a degenerate or a non-degenerate 2DEG, respectively.
To demonstrate the existence of spin currents due to asymmetric scattering we carry out the following experiments. Drude absorption is achieved using linearly polarized terahertz radiation directed along the growth direction of (001)-oriented heterostructures. The equilibrium spin polarization is obtained by an in-plane magnetic field B, which shifts the two parabolas of Fig. 1a vertically by ±g μBB/2. The photocurrent is measured both perpendicular and parallel to the magnetic field. Our set-up excludes other effects known to cause photocurrents: because linearly polarized radiation is used, all helicity-dependent spin photocurrents, such as the spin-galvanic effect4 and the circular photogalvanic effect5, are absent. In addition, photon drag and the linear photogalvanic effect are forbidden by symmetry for normal incidence on (001) heterostructures6.
The experiments are carried out on both (001)-oriented n-type GaAs/AlGaAs and InAs/AlGaSb two-dimensional structures grown by molecular beam epitaxy. The parameters of the samples are given in Table 1. Two pairs of ohmic contacts at the centre of the sample edges and lying along the  and y∥[110] directions have been prepared to measure the photocurrent (see Fig. 2b, inset). A high-power THz laser has been used to deliver 100 ns pulses with radiation power P up to 1 kW. Several wavelengths between 77 and 496 μm have been selected using NH3,D2O and CH3F as active media6. The samples are irradiated under normal incidence. The THz radiation causes indirect optical transitions within the lowest size-quantized subband. In the experiment, the angle α between the polarization plane of the light and the x axis is varied (see Fig. 3, upper panel inset). The external magnetic field with a maximum strength of B=0.6 T is applied parallel to the heterojunction interface along the [110] direction. The photocurrent in unbiased devices is measured via the voltage drop across a 50 Ω load resistor in a closed circuit with a storage oscilloscope. The measured current pulses of 100 ns duration reflect the corresponding laser pulses.
and y∥[110] directions have been prepared to measure the photocurrent (see Fig. 2b, inset). A high-power THz laser has been used to deliver 100 ns pulses with radiation power P up to 1 kW. Several wavelengths between 77 and 496 μm have been selected using NH3,D2O and CH3F as active media6. The samples are irradiated under normal incidence. The THz radiation causes indirect optical transitions within the lowest size-quantized subband. In the experiment, the angle α between the polarization plane of the light and the x axis is varied (see Fig. 3, upper panel inset). The external magnetic field with a maximum strength of B=0.6 T is applied parallel to the heterojunction interface along the [110] direction. The photocurrent in unbiased devices is measured via the voltage drop across a 50 Ω load resistor in a closed circuit with a storage oscilloscope. The measured current pulses of 100 ns duration reflect the corresponding laser pulses.
a,b, Photocurrent jx for sample 1 at By=0.3 T (a) and By=−0.3 T (b). The photocurrent  is excited by linearly polarized radiation of λ=280 μm under normal incidence. The solid lines are fits to jx=±c o n s t a n t at low T and jx∝±1/T at high T for By=±0.3 T, respectively. The inset in b shows the geometry of the experiment. c, Temperature dependence of the resistance. The decomposition of the resistance into mobility μ (triangles) and carrier density ns (circles) is shown for sample 2 in the inset. The decrease (increase) of resistance (mobility), R∝(nsμ)−1, with decreasing temperature is due to suppression of phonon scattering.
is excited by linearly polarized radiation of λ=280 μm under normal incidence. The solid lines are fits to jx=±c o n s t a n t at low T and jx∝±1/T at high T for By=±0.3 T, respectively. The inset in b shows the geometry of the experiment. c, Temperature dependence of the resistance. The decomposition of the resistance into mobility μ (triangles) and carrier density ns (circles) is shown for sample 2 in the inset. The decrease (increase) of resistance (mobility), R∝(nsμ)−1, with decreasing temperature is due to suppression of phonon scattering.
Data are obtained at By=0.3 T. Upper panel: photocurrent  at λ=280 μm and T=4.2, 85 and 295 K. The lines are fits according to jx=j1cos 2α+j2, see equations (3), (8) and (10). Lower panel: photocurrent
at λ=280 μm and T=4.2, 85 and 295 K. The lines are fits according to jx=j1cos 2α+j2, see equations (3), (8) and (10). Lower panel: photocurrent  measured at room temperature for λ=148 and 280 μm. The lines are fitted to jy=j3sin 2α, see equations (4), (9) and (10). The insets show the experimental geometries. An additional inset in the lower panel shows the wavelength dependence of the signal for transverse geometry. The full line shows jx∝λ2.
measured at room temperature for λ=148 and 280 μm. The lines are fitted to jy=j3sin 2α, see equations (4), (9) and (10). The insets show the experimental geometries. An additional inset in the lower panel shows the wavelength dependence of the signal for transverse geometry. The full line shows jx∝λ2.
Irradiation of the samples at B=0 does not lead—as expected—to any current. A photocurrent response is obtained only when B is applied. As described by equations (1) and (2) the current increases linearly with By due to the increasing spin polarization and changes sign on reversal of B. Corresponding data will be discussed below. The temperature and polarization dependences of the current were measured in all samples for two directions: along and perpendicular to the in-plane magnetic field. Figure 2 shows the typical temperature dependence of the photocurrent. Although the photocurrent is constant at low temperatures, it decreases as 1/T at temperatures above 100 K. As we show below, the peculiar temperature dependence is direct evidence that the current is driven by the spin polarization given by equation (2).
Before we discuss the corresponding microscopic origin in more detail we present the polarization dependences of the current perpendicular (Fig. 3, upper panel) and parallel (Fig. 3, lower panel) to By. The polarization dependence of the current j can be fitted by jx=j1cos2α+j2 for the transverse geometry and by jy=j3sin 2α for the longitudinal geometry. The overall polarization dependences of the photocurrent remain the same, independent of temperature and wavelength. An increased wavelength at constant intensity only results in an increased signal strength. The wavelength dependence for both configurations is described by j∝λ2 for the wavelengths used (see Fig. 3, lower panel inset) and reflects the spectral behaviour of Drude absorption, η(ω)∝1/ω2 at ω τp≫1 (see ref. 7). Here η(ω) is the 2DEG’s absorbance at frequency ω and τp is the momentum relaxation time.
The fact that an offset j2 is only observed for the transverse geometry is in accordance with the phenomenological theory of magnetic-field-induced photocurrents8. For normal incidence, the current components are described by


where I and e are the light intensity and polarization vector, respectively. The parameters C1 to C3 are coefficients determined by the C2v symmetry, relevant for (001)-oriented structures. The polarization-independent offset is described by the second term on the right-hand side of equation (3) and is only present for the transverse geometry. The only visible consequence of this contribution is the offset of jx in the upper panel of Fig. 3. The other terms on the right-hand sides of equations (3) and (4) yield polarization dependences in full agreement with experiments.
All experimental features, that is, the temperature and polarization dependences, are driven by the spin degree of freedom: for fixed polarization, the current is proportional to the frequency-dependent absorbance η(ω), momentum relaxation time τp, light intensity I and average spin S: j∝η(ω)I τpS. This type of expression for the temperature dependence is valid for fixed scattering mechanisms, for example, phonon or impurity scattering. To corroborate this claim and to obtain the polarization dependence microscopically, we calculated the magneto-induced photocurrent for impurity scattering within the framework of a spin-density matrix. The scattering-asymmetry-induced contribution to the photocurrents is given by

Here vk=ħk/m* is the electron velocity, ħ is the reduced Planck constant, m* is the effective electron mass, δ fs k is the fraction of the carrier distribution function stemming from optical transitions in the spin subband s, Ms k,s k′ is the matrix element of the indirect optical transition, fs k is the equilibrium distribution function, ɛk=ħ2k2/2m* is the electron kinetic energy for in-plane motion and s is an index enumerating subbands with spin states ±1/2 along the direction of the external magnetic field. To first order in spin–orbit interaction, the compound matrix element for the indirect optical transitions via impurity scattering has the form9

Here A=A e is the vector potential of the electromagnetic wave, c is the speed of light and Vk k′ is the scattering matrix element given by10

where the term V0 describes the conventional spin-independent scattering and the term proportional to the second-rank pseudo-tensor Vα β yields the asymmetric spin-dependent contribution linear in k responsible for the effects described here. The first term on the right-hand side of equation (6) describes transitions involving virtual intermediate states in the conduction band, whereas the second term corresponds to transitions via virtual intermediate states in the valence band.
For C2v point-group symmetry there are only two non-zero components of the tensor Vα β: Vx y and Vy x. By using equations (5)–(7), an expression for the electric current j can be derived. We consider the free-carrier absorption to be accompanied by electron scattering from short-range static defects and assume therefore that the matrix element V0 and the coefficients Vα β are wavevector independent. As in experiments, we consider linearly polarized light at normal incidence and an in-plane magnetic field By resulting in an average spin Sy. Then, currents parallel and perpendicular to the magnetic field can be written as


where the photon energy ħω is assumed to be smaller than the characteristic energy  . Note that the polarization-independent part of equation (3) is missing here as our theory does not contain the relaxation process (Fig. 1b), which is responsible for the background signal of jx in the upper panel of Fig. 3.
. Note that the polarization-independent part of equation (3) is missing here as our theory does not contain the relaxation process (Fig. 1b), which is responsible for the background signal of jx in the upper panel of Fig. 3.
Equations (8) and (9) contain the polarization dependence for transverse and longitudinal orientation, respectively, given by

The observed polarization dependences are in full agreement with equations (8)–(10) (see fits in Fig. 3). Note that the polarization dependence of jx and jy is independent of temperature and wavelength. It is solely described by equations (3) and (4) and does not depend on the specific scattering mechanism of Drude absorption.
However, the different scattering mechanisms involved in Drude absorption are reflected in the temperature dependence of the photocurrent shown in Fig. 2. Although impurity scattering prevails at low temperatures, phonon scattering takes over for T>100 K and is then the dominant scattering mechanism11. For temperatures up to ≈25 K the current is constant. As for Drude absorption, η(ω)∝ns/τp at ω τp≫1 (see ref. 7) and at low temperatures S∝1/ɛF∝1/ns (see equation (2)), the current j/I∝τpη(ω)S is constant and independent of τp and ns. In further experiments we changed the carrier density at 4.2 K by visible and near-infrared light. For sample 1, for example, the carrier density (mobility) increases from 1.3×1011 cm−2 (1.7×106 cm2 V−1s−1) to 3.0×1011 cm−2 (4.1×106 cm2 V−1s−1) after illumination at low T. Although both ns and τp increase by a factor of 2, the photocurrent remains unchanged, thus confirming the above arguments. In addition, for T> 100 K the carrier density ns is roughly constant but S is now sufficiently well described by the Boltzmann distribution and hence S∝1/kBT, see equation (2). Therefore, the current j is proportional to ns/T and becomes temperature dependent, concordant with experiment. Fits to the data at low and high T are shown as solid lines in Fig. 2. The unusual temperature dependence of jx proves that the current is driven by the average spin (equations (1) and (2)). As shown in Fig. 2c, it is uncorrelated to the T dependence of the mobility, which dominates the resistance of our samples. In the intermediate range between 25 and 100 K, such simple analysis fails. There the scattering mechanism changes from impurity dominated to phonon dominated. This transition region has not yet been treated theoretically and is outside the scope of this letter.
The experiments, carried out on different samples, are summarized in Fig. 4. Using the setup shown in the upper panel in Fig. 3 for two fixed polarization directions, α=0∘ and 90∘, we obtain a linear increase of the corresponding photocurrent, shown in the upper panel of Fig. 4. By subtracting and adding the currents of both polarizations, the coefficients j1 (polarization-dependent amplitude) and j2 (polarization-independent background) can be extracted. Corresponding results of j1 (lower left panel) and j2 (lower right panel) for four different samples are shown. Owing to the larger g factor of sample 4 (InAs QW), causing larger average spin S, the currents are largest for this sample. The other three samples are GaAs-based heterostructures that differ in structural inversion asymmetry. Sample 1 is a heterojunction (see Table 1) which, owing to the triangular confinement potential, is expected to have the strongest SIA contribution. Samples 2 and 3 are QWs of the same width, asymmetrically and symmetrically modulation doped, with larger and smaller SIA strength, respectively. The fact that with decreasing strength of the SIA coupling coefficient (from samples 1–3) the currents become smaller is in excellent agreement with our picture of asymmetric-scattering-driven currents. The coupling strength constant controls the current via Vα β in equations (8) and (9) and equivalent expressions for other scattering mechanisms: the larger the coupling strength, the larger the effect of asymmetric scattering.
Finally, we would like to address the role of spin-dependent relaxation, shown in Fig. 1b. The absorption of radiation leads to electron gas heating. Owing to the spin-dependent asymmetry of scattering, energy relaxation rates for positive and negative kx are non-equal as indicated by bent arrows of different thickness and spin currents result. Like for Drude excitation, spin separation takes place and applying a magnetic field results in a net electric current. As indicated in Fig. 1a,b excitation- and relaxation-induced currents flow in opposite directions. Experimentally this is observed for all samples: j1 and j2 for each sample have consistently opposite signs.
In summary, we emphasize that all central experimental features of the terahertz photocurrent, namely, magnetic field, temperature, mobility and concentration dependences provide evidence that the observed effect is solely determined by the spin degree of freedom. Furthermore, our observations suggest that heating the electron gas by any means (microwaves, voltage and so on) is sufficient to generate spin currents. Our results demonstrate that spin-dependent scattering provides a new tool for spin manipulation.
References
Kato, Y., Myers, R. C., Gossard, A. C. & Awschalom, D. D. Observation of the spin Hall effect in semiconductors. Science 306, 1910–1913 (2004).
Wunderlich, J., Kaestner, B., Sinova, J. & Jungwirth, T. Experimental observation of the spin-Hall effect in a two-dimensional spin-orbit coupled semiconductor system. Phys. Rev. Lett. 94, 047204 (2005).
Tarasenko, S. A. & Ivchenko, E. L. Pure spin photocurrents in low-dimensional structures. Pis’ma Zh. Eksp. Teor. Fiz. 81, 292–296 (2005) ibid. JETP Lett. 81, 231–235 (2005).
Ganichev, S. D. et al. Spin-galvanic effect. Nature 417, 153–156 (2002).
Ganichev, S. D. et al. Conversion of spin into directed electric current in quantum wells. Phys. Rev. Lett. 86, 4358–4362 (2001).
Ganichev, S. D. & Prettl, W. Intense Terahertz Excitation of Semiconductors (Oxford Univ. Press, Oxford, 2006).
Seeger, K. Semiconductor Physics (Springer, Wien, 1997).
Bel’kov, V. V. et al. Magneto-gyrotropic photogalvanic effects in semiconductor quantum wells. J. Phys. Condens. Matter 17, 3405–3428 (2005).
Tarasenko, S. A. Spin orientation of a two-dimensional electron gas by a high-frequency electric field. Phys. Rev. B 73, 115317 (2006).
Ivchenko, E. L. & Pikus, G. E. Optical orientation of free carriers spins and photogalvanic effects in gyrotropic crystals. Izv. Akad. Nauk SSSR 47, 2369–2372 (1983) ibid. Bull. Acad. Sci. USSR 47, 81–84 (1983).
Kelly, M. J. Low-Dimensional Semiconductors (Clarendon, Oxford, 1995).
Acknowledgements
We would like to thank I. Gronwald for help in sample preparation. This work was supported by the DFG through Project GA-501/5, Research Unit FOR370 and Collaborative Research Center SFB689, the RFBR and programs of the RAS. S.G. thanks the HBS and S.A.T. thanks the Foundation ‘Dynasty’–ICFPM and the President Grant for young scientists for support.
Author information
Authors and Affiliations
Contributions
Project planning, model and writing: S.D.G., V.V.B., S.A.T., E.L.I., D.W., W.W., W.P.; experiments and data analysis: S.D.G., V.V.B., S.N.D., S.G., Ch.H.; sample growth and characterization: W.W., Ch.G., D.S., J.S., J.B., G.B.; theory: S.A.T., E.L.I.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Ganichev, S., Bel’kov, V., Tarasenko, S. et al. Zero-bias spin separation. Nature Phys 2, 609–613 (2006). https://doi.org/10.1038/nphys390
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys390
This article is cited by
-
Polarization-controlled tunable directional spin-driven photocurrents in a magnetic metamaterial with threefold rotational symmetry
Nature Communications (2022)
-
Spin photogalvanic effect in two-dimensional collinear antiferromagnets
npj Quantum Materials (2021)
-
Two-dimensional centrosymmetrical antiferromagnets for spin photogalvanic devices
npj Quantum Information (2021)
-
Switchable magnetic bulk photovoltaic effect in the two-dimensional magnet CrI3
Nature Communications (2019)
-
Observation of anomalous linear photogalvanic effect and its dependence on wavelength in undoped InGaAs/AlGaAs multiple quantum well
Nanoscale Research Letters (2014)