Abstract
Quantum spin fluctuation in a low-dimensional or frustrated magnet breaks magnetic ordering while keeping spin correlation1. Such fluctuation has been a central topic in magnetism because of its relevance to high-Tc superconductivity2 and topological states3. However, utilizing such spin states has been quite difficult. In a one-dimensional spin-1/2 chain, a particle-like excitation called a spinon is known to be responsible for spin fluctuation in a paramagnetic state. Spinons behave as a Tomonaga–Luttinger liquid at low energy, and the spin system is often called a quantum spin chain4. Here we show that a quantum spin chain generates and carries spin current, which is attributed to spinon spin current. This is demonstrated by observing an anisotropic negative spin Seebeck effect5,6,7,8,9,10 along the spin chains in Sr2CuO3. The results show that spin current can flow even in an atomic channel owing to long-range spin fluctuation.
Similar content being viewed by others
Main
The flow of electron spins is defined as spin current. In condensed matter science, the transport properties of spin current have attracted considerable interest since the discovery of various spin-current phenomena11,12. However, in spintronics13, finding materials that can carry spin angular momentum efficiently is of critical importance, especially for integrated microscopic devices.
So far, two types of spin current, conduction-electron spin current and spin-wave spin current, have experimentally been explored. The former is mediated by the motion of electrons in metals and semiconductors. Thus, its velocity and propagation length are limited by electron spin diffusion. In the latter type14,15, spin waves, wave-like propagation of spin motions in magnets, carry spin angular momentum. Its excitation gap is equal to a spin-wave gap, proportional to the magnetic anisotropy. In addition, spin-wave spin current can exist even in insulators in which spin relaxation via conduction electrons is absent. This is an advantage that may realize fast and long-range spin-current transmission, opening a new field of insulator-based spintronics. However, spin-wave spin current in classical magnets may not be suitable for microscopic devices, since handling spin waves becomes difficult when devices are miniaturized toward atomic scale. In ferromagnets, spontaneous magnetization brings about significant stray fields, causing crosstalk. However, in antiferromagnetic systems, spin ordering patterns should be broken or interfered when a device is in atomic scale; in both these cases, spin waves become vulnerable. Therefore, to realize spin-current transport in microscopic devices, spin ordering is expected to vanish while maintaining a strong interaction between spins.
Here, we would like to introduce a new type of spin current: spinon spin current, which may provide a channel for spin transmission based on quantum fluctuation without spin ordering. Spinons generally refer to magnetic elementary excitations in quantum spin liquids1. When the system size of a magnet is reduced to atomic scale, quantum spin fluctuation manifests itself and dominates spin properties. The most typical example is found in one-dimensional spin-1/2 chains realized in some oxides, such as an insulator Sr2CuO3 (refs 16,17,18). In Sr2CuO3, each Cu2+ ion carries spin-1/2 and they are connected to each other linearly along the b axis, as shown in Fig. 1a. Because of the one-dimensionality, the fluctuation of the spin-1/2 is so strong that it prevents magnetic ordering. As a result, antiferromagnetic interaction embedded in the chain creates a paramagnetic state accompanied by strong spin-singlet correlation. Spin excitation from the correlated ground state has been predicted to be particle-like and to exhibit zero excitation gap, and this excitation is known as a spinon. This gapless feature is robust against external magnetic fields and magnetic anisotropy. Furthermore, theories have predicted that the correlation of spinons is of a markedly long length scale; even infinite correlation length is predicted in the context of the Tomonaga–Luttinger (TL) liquid theories4. These indicate that in such a system spin current may propagate through a long distance via spinons.
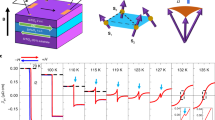
a, Quantum spin chains in Sr2 CuO3. Quantum spin chains along the b axis consist of Cu2+ ions sharing O2− ions. b, Schematic illustration of the experimental set-up. The sample consists of a single-crystalline Sr2CuO3 and a Pt film. A temperature gradient, ∇T, is generated along the spin chains (b axis) by applying a temperature difference, ΔT. B denotes an external magnetic field and T the system temperature. c, Configuration of quantum spin chains in the experimental set-up. A Cu–O chain is set along ∇T. d, Schematic illustration of the inverse spin Hall effect. An electric field, ESHE, arises in the direction of Is × σ in Pt. Here Is and σ are the spatial direction and the spin-polarization direction of spin current, respectively. e, B dependence of  , the voltage V divided by the temperature difference ΔT, in a Pt film put on a single-crystalline MgO. The dashed lines are fits to the data points. f, T dependence of
, the voltage V divided by the temperature difference ΔT, in a Pt film put on a single-crystalline MgO. The dashed lines are fits to the data points. f, T dependence of  measured in Pt/MgO. The error bars represent the 68% confidence level (±s.d.).
measured in Pt/MgO. The error bars represent the 68% confidence level (±s.d.).
To drive the spin current, one of the most versatile methods is to use a longitudinal spin Seebeck effect7,8,10 (LSSE). LSSE refers to the generation of spin current as a result of a temperature gradient applied across the junction between a magnet, typically a magnetic insulator, and a metal film, typically Pt. The temperature gradient injects spin current into the metal from the magnet. The injected spin current is converted into electric voltage via the inverse spin Hall effect19,20,21 (ISHE) in the metal. The voltage is generated perpendicular to the spin polarization and the propagation directions of the spin current. By measuring the voltage generated, the method enables sensitive detection of spin current. The amplitude of the injected spin current is proportional to the non-equilibrium accumulation of spin angular momentum at the interface in the magnet. In this study, we utilized the LSSE to extract spin current from a spinon system.
Spinon-induced LSSE is characterized by a distinguished feature: theory predicts that the sign of angular momentum due to a spinon LSSE is opposite to that of the conventional spin-wave-induced LSSE at low temperatures under magnetic fields. The opposite spin angular momentum is mainly due to the singlet correlation increasing with decreasing temperature in the present spinon system in contrast to ferromagnetic correlation growing in classical magnets. Detailed theoretical calculations using a microscopic model reproduce this intuition, which is described below. By exploiting these properties of LSSE, we observed spin-current generation and transmission in Sr2CuO3, a typical paramagnetic insulator in which the spinon picture has well been established1.
Figure 1b is a schematic illustration of the experimental set-up used in this study. The sample consists of a single crystal of Sr2CuO3 and a Pt thin film. The Pt film is used as a spin-current detector based on ISHE, in which spin current is converted into an electromotive force, ESHE (Fig. 1d). The spin chains in Sr2CuO3 are set normal to the Pt film plane (Fig. 1c). A temperature gradient, ∇T, was generated along the spin chains by applying the temperature difference ΔT between the top of the Pt film and the bottom of Sr2CuO3 (see also Fig. 1b). The voltage difference V is measured between the ends of the Pt film while applying an in-plane field, B.
First, we measured the ΔT-induced voltage in a Pt film without Sr2CuO3. In this simple film, the voltage is produced via the normal Nernst effect of Pt alone22. In Fig. 1e, we show the magnetic field B dependence of the voltage at several temperatures. The voltage  (the voltage V divided by the temperature difference ΔT) was found to be proportional to B. In Fig. 1f, we show the temperature T dependence of the slope
(the voltage V divided by the temperature difference ΔT) was found to be proportional to B. In Fig. 1f, we show the temperature T dependence of the slope  (that is, the Nernst coefficient of Pt). The sign of
(that is, the Nernst coefficient of Pt). The sign of  is positive for the entire range of T, showing that the sign of the normal Nernst effect of Pt is positive in the whole temperature range in the present set-up.
is positive for the entire range of T, showing that the sign of the normal Nernst effect of Pt is positive in the whole temperature range in the present set-up.
The temperature dependence of  for Pt changes dramatically when Sr2CuO3 is attached to Pt. Figure 2a shows the T dependence of
for Pt changes dramatically when Sr2CuO3 is attached to Pt. Figure 2a shows the T dependence of  for Pt/Sr2CuO3. The sign of
for Pt/Sr2CuO3. The sign of  is positive around room temperature, the same sign as the normal Nernst effect in the simple Pt film. With decreasing T, surprisingly, the sign of
is positive around room temperature, the same sign as the normal Nernst effect in the simple Pt film. With decreasing T, surprisingly, the sign of  reverses around 180 K and is negative below this temperature (see also Fig. 2c, d). In addition, another sign reversal takes place with decreasing T further and
reverses around 180 K and is negative below this temperature (see also Fig. 2c, d). In addition, another sign reversal takes place with decreasing T further and  changes to positive below about 5 K, which is comparable to the Néel temperature of Sr2CuO3 (ref. 16). These sign reversals show that the negative
changes to positive below about 5 K, which is comparable to the Néel temperature of Sr2CuO3 (ref. 16). These sign reversals show that the negative  component appears by attaching the insulator Sr2CuO3 and that it dominates at low temperatures, but disappears following the Néel ordering. The negative sign of
component appears by attaching the insulator Sr2CuO3 and that it dominates at low temperatures, but disappears following the Néel ordering. The negative sign of  cannot be explained by the normal Nernst effect of Pt, but it is the very feature of the aforementioned spinon LSSE. On the other hand, the sign of the LSSE voltage for Pt/conventional ferromagnets, ferrimagnets or antiferromagnets is the same as that of the normal Nernst effect of Pt in the present set-up7,8,23. The sign reversal around 180 K is attributed to a competition between such a negative
cannot be explained by the normal Nernst effect of Pt, but it is the very feature of the aforementioned spinon LSSE. On the other hand, the sign of the LSSE voltage for Pt/conventional ferromagnets, ferrimagnets or antiferromagnets is the same as that of the normal Nernst effect of Pt in the present set-up7,8,23. The sign reversal around 180 K is attributed to a competition between such a negative  component and the positive component due to the normal Nernst effect of Pt.
component and the positive component due to the normal Nernst effect of Pt.
a, T dependence of  measured in Pt/Sr2CuO3. The data for Pt/MgO are also presented (see also Fig. 1f). The error bars represent the 68% confidence level (±s.d.). The lower and upper insets show sign reversal at about 180 K and 5 K, respectively. b, Experimental set-ups. In Pt/MgO (upper panel), the electric field ENNE arises via the normal Nernst effect in Pt. In Pt/Sr2CuO3 (lower panel), the electric field ESHE also arises via the inverse spin Hall effect in Pt. c,d, B dependence of
measured in Pt/Sr2CuO3. The data for Pt/MgO are also presented (see also Fig. 1f). The error bars represent the 68% confidence level (±s.d.). The lower and upper insets show sign reversal at about 180 K and 5 K, respectively. b, Experimental set-ups. In Pt/MgO (upper panel), the electric field ENNE arises via the normal Nernst effect in Pt. In Pt/Sr2CuO3 (lower panel), the electric field ESHE also arises via the inverse spin Hall effect in Pt. c,d, B dependence of  measured in Pt/Sr2CuO3 at various temperatures. The lines are fits to the data points. The inset to d shows the data taken up to 9 T at 15 K. e–g, Dependence of V on ΔT at 260 K (e), 15 K (f) and 3 K (g) at 1 T. In all of these cases, V is proportional to ΔT.
measured in Pt/Sr2CuO3 at various temperatures. The lines are fits to the data points. The inset to d shows the data taken up to 9 T at 15 K. e–g, Dependence of V on ΔT at 260 K (e), 15 K (f) and 3 K (g) at 1 T. In all of these cases, V is proportional to ΔT.
The sign reversal of  was found to be related to spin-current injection from Sr2CuO3 as follows. In Fig. 3a,
was found to be related to spin-current injection from Sr2CuO3 as follows. In Fig. 3a,  measured for W/Sr2CuO3 is plotted as a function of T (red data points), where W exhibits negative ISHE; the sign of ISHE of W is opposite to that of Pt (ref. 24). In W/Sr2CuO3,
measured for W/Sr2CuO3 is plotted as a function of T (red data points), where W exhibits negative ISHE; the sign of ISHE of W is opposite to that of Pt (ref. 24). In W/Sr2CuO3,  is always positive and does not exhibit any sign reversal (see also Fig. 3c, d), and remarkably, a V/ΔT peak with positive sign appears around 20 K (pink arrow in Fig. 3a): the opposite peak sign to that of Pt/Sr2CuO3 (blue arrow in Fig. 3a). The sign change between W and Pt shows that the low-temperature V/ΔT signal is attributed mainly to ISHE due to spin current injected from Sr2CuO3. We note that the peak temperature ∼20 K is not the same as the temperature at which the spin thermal conductivity reaches its maximum (∼50 K for a high-purity Sr2CuO3; ref. 25); similar results were reported for conventional spin waves in ferrimagnet Y3Fe5O12 (refs 10,26).
is always positive and does not exhibit any sign reversal (see also Fig. 3c, d), and remarkably, a V/ΔT peak with positive sign appears around 20 K (pink arrow in Fig. 3a): the opposite peak sign to that of Pt/Sr2CuO3 (blue arrow in Fig. 3a). The sign change between W and Pt shows that the low-temperature V/ΔT signal is attributed mainly to ISHE due to spin current injected from Sr2CuO3. We note that the peak temperature ∼20 K is not the same as the temperature at which the spin thermal conductivity reaches its maximum (∼50 K for a high-purity Sr2CuO3; ref. 25); similar results were reported for conventional spin waves in ferrimagnet Y3Fe5O12 (refs 10,26).
a, T dependence of  measured in W/Sr2CuO3. The data for Pt/Sr2CuO3 are also presented for comparison. The error bars represent the 68% confidence level (±s.d.). b, Experimental set-ups for W/Sr2CuO3 (upper panel) and Pt/Sr2CuO3 (lower panel). The directions of ESHE are opposite between W and Pt as highlighted by the red and blue arrows. c,d, B dependence of
measured in W/Sr2CuO3. The data for Pt/Sr2CuO3 are also presented for comparison. The error bars represent the 68% confidence level (±s.d.). b, Experimental set-ups for W/Sr2CuO3 (upper panel) and Pt/Sr2CuO3 (lower panel). The directions of ESHE are opposite between W and Pt as highlighted by the red and blue arrows. c,d, B dependence of  measured in W/Sr2CuO3 at various temperatures. The lines are fits to the data points. e, T dependence of
measured in W/Sr2CuO3 at various temperatures. The lines are fits to the data points. e, T dependence of  under ∇T perpendicular to the spin chains (a axis, green). The result for ∇T along the spin chains (b axis, blue) is shown for comparison. The inset shows the data for W/Sr2CuO3. The error bars represent the 68% confidence level (±s.d.). f, Experimental set-ups for measuring the chain-direction dependence of voltage. The bottom panel shows the directions of ∇T with respect to the Cu–O chains. g,h, B dependence of
under ∇T perpendicular to the spin chains (a axis, green). The result for ∇T along the spin chains (b axis, blue) is shown for comparison. The inset shows the data for W/Sr2CuO3. The error bars represent the 68% confidence level (±s.d.). f, Experimental set-ups for measuring the chain-direction dependence of voltage. The bottom panel shows the directions of ∇T with respect to the Cu–O chains. g,h, B dependence of  measured under ∇T along the a axis (g) and along the b axis (h) in Pt/Sr2CuO3. The lines are fits to the data points.
measured under ∇T along the a axis (g) and along the b axis (h) in Pt/Sr2CuO3. The lines are fits to the data points.
In Fig. 3e,  was compared between the ∇T ∥ b-axis and the ∇T ⊥ b-axis configurations. The b axis is the spin-chain direction of Sr2CuO3, and thus in the ∇T ∥ b-axis (∇T ⊥ b-axis) configuration, the heat current flows parallel (normal) to the spin chains. Clearly, the negative
was compared between the ∇T ∥ b-axis and the ∇T ⊥ b-axis configurations. The b axis is the spin-chain direction of Sr2CuO3, and thus in the ∇T ∥ b-axis (∇T ⊥ b-axis) configuration, the heat current flows parallel (normal) to the spin chains. Clearly, the negative  peak observed in Pt/Sr2CuO3 is suppressed when ∇T ⊥ b axis: the amplitude of
peak observed in Pt/Sr2CuO3 is suppressed when ∇T ⊥ b axis: the amplitude of  at 20 K is one order of magnitude less than that in the ∇T ∥ b-axis configuration (see also Fig. 3g, h). The suppression was confirmed also in W/Sr2CuO3 (see the inset to Fig. 3e). The result shows that the spin-current injection from Sr2CuO3 takes place only when heat current is applied along the spin chain; the spin angular momentum flowing along the spin chains of Sr2CuO3 dominates the spin-current injection observed in the present study. The small negative signal of
at 20 K is one order of magnitude less than that in the ∇T ∥ b-axis configuration (see also Fig. 3g, h). The suppression was confirmed also in W/Sr2CuO3 (see the inset to Fig. 3e). The result shows that the spin-current injection from Sr2CuO3 takes place only when heat current is applied along the spin chain; the spin angular momentum flowing along the spin chains of Sr2CuO3 dominates the spin-current injection observed in the present study. The small negative signal of  for the ∇T ⊥ b axis (Fig. 3e) might be attributed to an inevitable slight misalignment in the ∇T direction from the b axis (≤6°). We also note that the thermal conductivity and magnetic susceptibility of Sr2CuO3 are almost isotropic along the a and b axes18, and therefore, the voltage suppression cannot be attributed to a reduction in the magnitude of either ∇T or the field-induced magnetic moment. The negative and anisotropic LSSE is evidence that spin current is generated and conveyed by spinons through the spin chains of Sr2CuO3. Although seemingly similar results were reported for several three-dimensional materials, or Gd3Fe5O12 and DyScO3, the origins are completely different from that of the spinon LSSE. The negative sign of LSSE observed in the ferrimagnet Gd3Fe5O12 is attributed to competition in the spin injection between the different ordered magnetic ions27; in contrast, the magnetic ions of Sr2CuO3 are Cu2+ alone along with spin fluctuation down to ∼5 K. Additionally, the anisotropic LSSE in a paramagnetic state of the antiferromagnet DyScO3 is due simply to the strong anisotropy of the magnetic susceptibility while an origin of the negative sign remains to be elucidated22.
for the ∇T ⊥ b axis (Fig. 3e) might be attributed to an inevitable slight misalignment in the ∇T direction from the b axis (≤6°). We also note that the thermal conductivity and magnetic susceptibility of Sr2CuO3 are almost isotropic along the a and b axes18, and therefore, the voltage suppression cannot be attributed to a reduction in the magnitude of either ∇T or the field-induced magnetic moment. The negative and anisotropic LSSE is evidence that spin current is generated and conveyed by spinons through the spin chains of Sr2CuO3. Although seemingly similar results were reported for several three-dimensional materials, or Gd3Fe5O12 and DyScO3, the origins are completely different from that of the spinon LSSE. The negative sign of LSSE observed in the ferrimagnet Gd3Fe5O12 is attributed to competition in the spin injection between the different ordered magnetic ions27; in contrast, the magnetic ions of Sr2CuO3 are Cu2+ alone along with spin fluctuation down to ∼5 K. Additionally, the anisotropic LSSE in a paramagnetic state of the antiferromagnet DyScO3 is due simply to the strong anisotropy of the magnetic susceptibility while an origin of the negative sign remains to be elucidated22.
Finally, we turn to a theoretical formulation of the spinon LSSE in the present system. On the basis of a microscopic theory for LSSE28 (see Supplementary Sections A and B), the spin current Is injected from a magnet to a metal is given by

where ω is the angular frequency, δT is the temperature difference between the magnet and the metal, T is the mean value of the two temperatures, and A is a material-dependent factor (see Supplementary Section B). X−+ and χ−+ denote dynamical spin susceptibilities of the magnet and the metal, respectively. This formula can be applied to various magnetic phases (either magnetically ordered or disordered). We note that phenomenological transport theories for LSSE9 have also been developed and applied to ordered magnets, and in the formula (1), spinon coherent dynamics with a long mean free path is taken into account via the susceptibility X−+(ω). In low-dimensional transport phenomena such as the present spin-chain LSSE, an effect of disorder29 is generally relevant in the low-energy limit, while LSSE is a phenomenon driven by a finite temperature and large thermal conduction carried by spinons was observed in Sr2CuO3 (refs 17,18). These allow us to omit disorder effects within the framework of practical approximation.
Since the metal susceptibility χ−+ is well described by a diffusion type function proportional to ω (ref. 28), computation of X−+ is the remaining task to obtain the accurate spin current. The low-energy physics with strong singlet correlation of a spin-1/2 AF chain is captured by the TL liquid theory4. In the low-energy region, it enables us to calculate X−+ without any fitting parameters. However, the computed susceptibility is an odd function of ω even at finite B because of the linearized spinon dispersion. As a result, the linearized standard TL liquid theory leads to zero spin current. To obtain the accurate value of spin current, we consider the actual spinon dispersion beyond the linear approximation. In fact, the spinon dispersion is known to be curved at finite frequencies30 and LSSE is driven by finite-frequency spinons. Combining the curved dispersion with the TL liquid theory, we obtain a finite spin current, shown in Fig. 4. In Fig. 4, we also show a result for a ferromagnetic LSSE obtained by calculating the spin current Is for a three-dimensional ferromagnet (see Supplementary Section C). The spinon Is is found to be B-linear and the linearity continues up to very high fields (∼100 T) owing to the robust gapless excitation of spinons with the large exchange coupling (∼2,000 K); consistent with our experimental results (see also the inset to Fig. 2d, confirming the B-linearity up to 9 T). Most importantly, the sign of the spinon Is is opposite to that of the spin-wave Is, which captures the marked feature observed experimentally. This sign difference is attributed to whether the dominant weight of ImX−+(ω) is located in the positive or negative ω region (see Supplementary Sections B–D). Since the weight of ImX−+(ω) in the positive (negative) ω region corresponds to down-spin (up-spin) carriers, the sign difference is due to the opposite spin polarization carried by net spin carriers.
B dependence of spin current (Is) generated via spinon SSE and ferromagnetic SSE. For the spinon (ferromagnetic) SSE calculation, exchange coupling, J, was set at −2,000 K (+50 K), which is a typical value of Sr2CuO3 (Y3Fe5O12). A sample temperature, T, was set at 20 K. The amplitude of the ferromagnetic Is is multiplied by 10−4.
Methods
Sample preparation.
The single-crystalline Sr2CuO3 was grown from primary compounds SrCO3 and CuO with 99.999% by a travelling-solvent floating-zone method18. The single-crystalline Sr2CuO3 was cut into a cuboid 5 mm long, 1 mm wide and 1 mm thick. The surface of the Sr2CuO3 was polished mechanically in a glove box filled with N2 gas. We found that exposure of the sample to air causes deterioration of the sample, since the surface of Sr2CuO3 reacts rapidly with moisture25. The 7-nm-thick Pt film was then sputtered on the polished surface (5 × 1 mm2) of the Sr2CuO3 in an Ar atmosphere.
Voltage measurement.
Voltage data were taken in a Physical Properties Measurement System (Quantum Design). The Pt (W)/Sr2CuO3 sample was sandwiched by sapphire plates and the bottom of the sample was thermally anchored at the system temperature T. The temperature gradient ∇T was generated by applying a charge current to a chip resistor (100 Ω) on the sapphire plate attached to the metal film. The temperature difference ΔT between the sapphire plates was set to be ΔT/T < 0.1 at each system temperature T. Two electrodes were attached to both the ends of the metal film to measure the voltage. An external magnetic field was applied normal to the direction of ∇T as well as the direction across the two electrodes.
Data availability.
The data that support the plots within this paper and other findings of this study are available from the corresponding authors on request.
References
Diep, H. T. (ed.) Frustrated Spin Systems (World Scientific, 2013).
Anderson, P. W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198 (1987).
Wen, X. G. Quantum Field Theory of Many-Body Systems: From the Origin of Sound to an Origin of Light and Electrons (Oxford Univ. Press, 2004).
Giamarchi, T. Quantum Physics in One Dimension (Clarendon, 2004).
Uchida, K. et al. Observation of the spin Seebeck effect. Nature 455, 778–781 (2008).
Jaworski, C. M. et al. Observation of the spin-Seebeck effect in a ferromagnetic semiconductor. Nat. Mater. 9, 898–903 (2010).
Uchida, K. et al. Observation of longitudinal spin-Seebeck effect in magnetic insulators. Appl. Phys. Lett. 97, 172505 (2010).
Kikkawa, T. et al. Separation of longitudinal spin Seebeck effect from anomalous Nernst effect: determination of origin of transverse thermoelectric voltage in metal/insulator junctions. Phys. Rev. Lett. 88, 214403 (2013).
Rezende, S. M. et al. Magnon spin-current theory for the longitudinal spin-Seebeck effect. Phys. Rev. B 89, 014416 (2014).
Kikkawa, T. et al. Critical suppression of spin Seebeck effect by magnetic fields. Phys. Rev. B 92, 064413 (2015).
Slonczewski, J. C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 159, L1–L7 (1996).
Berger, L. Emission of spin waves by a magnetic multilayer traversed by a current. Phys. Rev. B 54, 9353–9358 (1996).
Žutić, I., Fabian, J. & Das Sarma, S. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323410 (2004).
Kajiwara, Y. et al. Transmission of electrical signals by spin-wave interconversion in a magnetic insulator. Nature 464, 262–266 (2010).
Cornelissen, L. J., Liu, J., Duine, R. A., Ben Youssef, J. & van Wees, B. J. Long-range transport of magnon spin information in a magnetic insulator at room temperature. Nat. Phys. 11, 1022–1026 (2015).
Motoyama, N., Eisaki, H. & Uchida, S. Magnetic susceptibility of ideal spin 1/2 Heisenberg antiferromagnetic chain systems, Sr2CuO3 and SrCuO2 . Phys. Rev. Lett. 76, 3212–3215 (1996).
Sologubenko, A. V., Giannò, K. & Ott, H. R. Heat transport by lattice and spin excitations in the spin-chain compounds SrCuO2 and Sr2CuO3 . Phys. Rev. B 64, 054412 (2001).
Kawamata, T. et al. Evidence for ballistic thermal conduction in the one-dimensional S = 1/2 Heisenberg antiferromagnetic spin system Sr2CuO3 . J. Phys. Soc. Jpn 77, 034607 (2008).
Saitoh, E., Ueda, M., Miyajima, H. & Tatara, G. Conversion of spin current into charge current at room temperature: inverse spin-Hall effect. Appl. Phys. Lett. 88, 182509 (2006).
Valenzuela, S. O. & Tinkham, M. Direct electronic measurement of the spin Hall effect. Nature 442, 176–179 (2006).
Kimura, T., Otani, Y., Sato, T., Takahashi, S. & Maekawa, S. Room-temperature reversible spin Hall effect. Phys. Rev. Lett. 98, 156601 (2007).
Wu, S. M., Pearson, J. E. & Bhattacharya, A. Paramagnetic spin Seebeck effect. Phys. Rev. Lett. 114, 186602 (2015).
Seki, S. et al. Thermal generation of spin current in an antiferromagnet. Phys. Rev. Lett. 115, 266601 (2015).
Hoffmann, A. Spin Hall effects in metals. IEEE Trans. Magn. 49, 5172–5193 (2013).
Hlubek, N. et al. Spinon heat transport and spin-phonon interaction in the spin-1/2 Heisenberg chain cuprates Sr2CuO3 and SrCuO2 . J. Stat. Mech. 3, P03006 (2012).
Boona, S. R. & Heremans, J. P. Magnon thermal mean free path in yttrium iron garnet. Phys. Rev. B 90, 064421 (2014).
Geprägs, S. et al. Origin of the spin Seebeck effect in compensated ferrimagnets. Nat. Commun. 7, 10452 (2015).
Adachi, H., Ohe, J., Takahashi, S. & Maekawa, S. Linear-response theory of spin Seebeck effect in ferromagnetic insulators. Phys. Rev. B 83, 094410 (2011).
Giamarchi, T. & Schulz, H. J. Anderson localization and interactions in one-dimensional metals. Phys. Rev. B 37, 325–340 (1988).
Müller, G., Thomas, H., Beck, H. & Bonner, J. C. Quantum spin dynamics of the antiferromagnetic linear chain in zero and nonzero magnetic field. Phys. Rev. B 24, 1429–1467 (1981).
Acknowledgements
We thank Y. Ohnuma, N. Yokoi and K. Sato for valuable discussions. This work is supported by ERATO-JST ‘Spin Quantum Rectification Project’, Japan, Grant-in-Aid for Scientific Research on Innovative Area ‘Nano Spin Conversion Science’ (No. 26103005), PRESTO ‘Phase Interfaces for Highly Efficient Energy Utilization’ from JST, Japan, Grant-in-Aid for Challenging Exploratory Research (No. 16K13827), and Grant-in-Aid for Scientific Research (A) (No. 15H02012) from MEXT, Japan. D.H. is supported by the Yoshida Scholarship Foundation through the Doctor 21 programme.
Author information
Authors and Affiliations
Contributions
D.H. and E.S. designed the experiments; T.K. grew single crystals used in the study; D.H. collected and analysed the data; K.-i.U. and R.I. supported the experiments; M.S. developed the theoretical explanations; S.M., Y.K. and E.S. supervised the study; D.H., M.S., Y.S. and E.S. wrote the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 534 kb)
Rights and permissions
About this article
Cite this article
Hirobe, D., Sato, M., Kawamata, T. et al. One-dimensional spinon spin currents. Nature Phys 13, 30–34 (2017). https://doi.org/10.1038/nphys3895
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3895
This article is cited by
-
Momentum-resolved spin-conserving two-triplon bound state and continuum in a cuprate ladder
Communications Physics (2023)
-
The role of spin in thermoelectricity
Nature Reviews Physics (2023)
-
News and views (1&2)
AAPPS Bulletin (2023)
-
Chiral spintronics
Nature Reviews Physics (2021)
-
Probing resonating valence bond states in artificial quantum magnets
Nature Communications (2021)