Abstract
In crystals, energy band extrema in momentum space can be identified by a valley index. The internal quantum degree of freedom associated with valley pseudospin indices can act as a useful information carrier, analogous to electronic charge or spin1,2,3,4. Interest in valleytronics has been revived in recent years following the discovery of atomically thin materials such as graphene and transition metal dichalcogenides5,6,7. However, the valley coherence time—a crucial quantity for valley pseudospin manipulation—is difficult to directly probe. In this work, we use two-dimensional coherent spectroscopy to resonantly generate and detect valley coherence of excitons (Coulomb-bound electron–hole pairs) in monolayer WSe2 (refs 8,9). The imposed valley coherence persists for approximately one hundred femtoseconds. We propose that the electron–hole exchange interaction provides an important decoherence mechanism in addition to exciton population recombination. This work provides critical insight into the requirements and strategies for optical manipulation of the valley pseudospin for future valleytronics applications.
Similar content being viewed by others
Main
Group-VI transition metal dichalcogenides (TMDs) with 2H structure (for example, MX2, M = Mo, W; X = S, Se) are a particularly intriguing class of semiconductors when thinned down to monolayers6,7. The valence and conduction band extrema are located at both K and K′ points at the corners of the hexagonal Brillouin zone, as illustrated in Fig. 1a. The degenerate K and K′ points are related to each other by time reversal symmetry and give rise to the valley degree of freedom (DoF) of the band-edge electrons and holes. Strong Coulomb interactions lead to the formation of excitons with remarkably large binding energies due to the heavy effective mass and reduced dielectric screening in monolayer TMDs (refs 10,11,12). An exciton as a bound electron–hole pair inherits the valley DoF. Because of valley-dependent optical selection rules, they can be excited only by σ+ (σ−) circularly polarized light at the K(K′) valley. Owing to its close analogy to spin4, the valley DoF can be considered as a pseudospin represented by a vector S on the Bloch sphere (Fig. 1b). The out-of-plane component Sz and in-plane component Sx, y describe the valley polarization and the coherent superposition of exciton valley states, respectively. After optical initialization, valley depolarization and decoherence are manifested by a reduction in the magnitudes of Sz and Sx, y, respectively.
a, Schematic band structure and optical selection rules in monolayer TMDs. Left-circularly polarized (σ+) and right-circularly polarized (σ−) light couples the valence and conduction bands at the K and K′ valleys, respectively. b, Bloch sphere representation of the valley pseudospin DoF. Exciton valley polarization and coherence are described by vectors Sz and Sx, y, respectively. Following initial optical excitation, valley depolarization and decoherence result in a decrease in the magnitude of Sz and Sx, y, respectively, with time.
The ability to coherently manipulate spins and pseudospins is at the heart of spintronics and valleytronics; however, previous investigations have focused mainly on the creation and relaxation of valley polarization using non-resonant photoluminescence (PL) or pump/probe spectroscopy techniques13,14,15,16,17,18,19. Optical excitation close to the lowest energy exciton resonance leads to nearly 100% valley polarization in monolayer TMDs such as MoS2 (refs 13,15,20). Time-resolved PL spectroscopy has revealed a few-picosecond valley polarization decay time, possibly limited by the temporal resolution of the technique17. Experiments based on pump/probe spectroscopy reported similar timescales; however, these measurements may be difficult to interpret owing to the fact that only the incoherent exciton population dynamics are probed, which can be sensitive to scattering between optically bright and dark excitons21. Even more intriguing are experiments that seem to show that exciton valley coherence—the coherent superposition of excitons in K and K′ valleys manifested as linearly polarized luminescence—is preserved in PL following non-resonant linearly polarized optical excitation8,9,22. However, steady-state PL does not reveal the timescale of the valley coherence dynamics.
Directly measuring the timescale over which quantum coherence in the valley pseudospin DoF is preserved remains an outstanding challenge in the field of valleytronics. Exciton valley coherence is a type of non-radiative quantum coherence, that is, coherence between states that are not dipole coupled. Probing exciton valley coherence therefore requires measurements that go beyond traditional linear spectroscopy techniques. In this paper, we examine exciton valley coherence dynamics in monolayer WSe2 using polarization-resolved optical two-dimensional coherent spectroscopy (2DCS; ref. 23). Using a sequence of laser pulses resonant with the exciton transition, we initialize and probe exciton valley coherence and find that it decays after ∼100 fs. The coherence time is faster than the exciton population recombination lifetime—also occurring on a sub-picosecond timescale—indicating the presence of additional valley decoherence channels. Following earlier work, we identify the electron–hole exchange interaction as an important decoherence mechanism in addition to exciton recombination24,25,26. Calculations taking the exchange interaction and the momentum-space distribution of excitons into account reproduce the measured valley coherence dynamics.
We examine monolayer WSe2 flakes ∼20 μm in lateral size grown on a sapphire substrate using chemical vapour deposition (see Supplementary Note 1 and Supplementary Fig. 1; ref. 27). Steady-state PL measurements are first performed to identify the exciton resonance and confirm that a high degree of valley polarization can be achieved. Circularly polarized PL spectra are shown in Fig. 2a for circularly polarized excitation tuned to 660 nm (1,879 meV). The spectra feature a high-energy peak associated with the A-exciton (X) and a lower-energy peak that we attribute to defect or impurity bound states (L). The laser spectrum for the coherent nonlinear optical experiments presented later is indicated by the dashed curve. Following σ+ polarized excitation, the PL emission intensity is primarily σ+ polarized, corresponding to a degree of exciton valley polarization PC = = 70 ± 2%. The high degree of circular polarization indicates robust initialization of excitons in either valley. We note that the degree of valley polarization in PL measurements varies significantly depending on the excitation wavelength. Thus, it cannot be used to infer valley polarization in the following experiments in which excitons are created resonantly. This PL measurement serves mainly as a familiar characterization method.
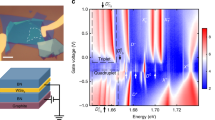
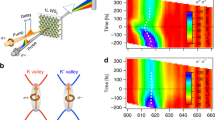
a, Low-temperature (10 K) PL spectra of monolayer WSe2 using σ+ polarized, 660 nm (1,879 meV) excitation for co- (σ+) and cross-circularly (σ−) polarized detection. The spectra feature two peaks associated with the A-exciton (X) and defect or impurity bound states (L). The laser spectrum used for the nonlinear experiments is indicated by the dashed line. b, The crystal ground state and two exciton states in the K and K′ valleys can be modelled by the three-level V system in the excitation picture. An exciton population in the K(K′) valley recombines with a rate ΓK (ΓK′). Coherence between the two exciton transitions decays with the valley decoherence rate given by γv. c, Schematic diagram of the 2DCS experiment. Three phase-stabilized pulses are focused onto the monolayer WSe2 sample with wavevectors k1, k2, and k3. The nonlinear interaction generates a four-wave mixing (FWM) signal that is radiated in the wavevector phase-matched direction ks. d, Illustration of the resonant generation and detection of exciton valley coherence. The first laser pulse creates a coherent superposition between the K-valley exciton and ground states (left panel), which is transferred to a non-radiative exciton valley coherence by the second pulse (middle panel). The third pulse converts the valley coherence to an exciton coherence in the K′ valley (right panel), which is optically detected.
In the excitation picture, excitons at K and K′ can be modelled as a three-level V -system, as shown in Fig. 2b. The exciton population decay rate in the K (K′) valley is given by ΓK (ΓK′) and reflects both radiative and non-radiative recombination. The valley coherence time (inversely proportional to γv) is limited by the lifetime of the exciton in either the K or K′ valley, and can be further reduced in the presence of additional dephasing mechanisms. Non-radiative quantum coherence has been investigated previously in several different systems, including atomic gases, semiconductor quantum wells, and quantum dots, and is responsible for lasing without inversion, electromagnetic induced transparency, and other interesting nonlinear phenomena28,29,30. If the two states involved are not energetically degenerate, the non-radiative coherence between them can be detected by means of quantum beats in time-resolved PL, pump/probe, or four-wave mixing spectroscopy. In these experiments, the coherence time can be extracted by examining the decay of the oscillation amplitude31,32.
In the case of degenerate valley excitons in TMDs, oscillatory quantum beats are absent and further care must be taken to separate non-radiative valley coherence from exciton recombination dynamics. To meet this challenge, we use optical 2DCS, which is akin to three-pulse four-wave mixing (or photon echo) spectroscopy with the addition of interferometric stabilization of the pulse delays (see Supplementary Note 2; ref. 33). 2DCS experiments are performed using a sequence of three phase-stabilized laser pulses separated by delays t1 and t2 (see Fig. 2c, d, Methods, and Supplementary Note 2). The coherent interaction of the pulses with the sample generates a four-wave mixing signal field ES(t1, t2, t3), which is spectrally resolved through heterodyne detection with a fourth phase-stabilized reference pulse. To avoid exciton–exciton interaction effects influencing the population recombination and valley coherence dynamics, the pump fluence at the sample is fixed at 1 μJ cm−2, which corresponds to an excitation density of ∼2 × 1011 excitons cm−2 and is in the χ(3) regime (see ref. 34). The population recombination and valley coherence dynamics are measured by recording ES as the delay t2 is stepped with interferometric precision while the delay t1 is held fixed. Fourier transformation of the signal with respect to t2 yields a two-dimensional coherent spectrum, ES(t1, ℏω2, ℏω3). This spectrum which correlates the ‘one-quantum’ exciton emission energy ℏω3 during delay t3 with the ‘zero-quantum’ energy ℏω2 of the system during the delay t2. Both population relaxation and non-radiative coherence evolution occur during the time delay t2. The experiments are performed at 10 K and low average excitation power to minimize exciton–phonon and exciton–exciton interaction broadening34.
Experiments using pulse sequences with carefully chosen polarization combinations provide information on both exciton population relaxation and valley coherence dynamics. We first present a 2D spectrum in which all of the excitation pulses and the detected signal are co-circularly polarized (σ+). In this case, the first two pulses create an exciton population in the K valley that decays with a rate given by ΓK. After a delay t2, the third pulse transfers the remaining population to a configuration with optical coherence between the exciton and ground states that radiates as the four-wave mixing signal field ES. The spectrum is shown in Fig. 3a, where the exciton emission energy (ℏω3) and zero-quantum energy (ℏω2) are on the horizontal and vertical axes, respectively. The spectrum features a single peak at an emission energy of 1,720 meV, consistent with the exciton resonance in the photoluminescence spectrum in Fig. 2a. The peak is centred at ℏω2 = 0 meV, because the system is excited to an incoherent population state in the K valley—that is, the phase does not evolve during the delay t2. A slice along the zero-quantum energy axis is shown in Fig. 3b (dashed curve), which is fitted by a square root Lorentzian function35. The half-width at half-maximum (HWHM) of the fit provides a measure of ΓK, which is equal to 3.4 ± 0.2 meV (T1 = ℏ/ΓK = 190 ± 10 fs), consistent with previous lifetime measurements of CVD-grown WSe2. Both radiative and non-radiative recombination contribute to the population decay.
a, The exciton population relaxation rate ΓK can be extracted from the 2D spectrum using co-circular polarization (σ+) of all excitation pulses and detected signal. The amplitude spectrum features a single peak at ℏω3 = 1,720 meV associated with the emission of excitons in the K valley. The HWHM along the zero-quantum energy axis ℏω2 provides a measure of the exciton population decay rate ΓK = 3.4 ± 0.2 meV. A slice along the white dashed line is shown in b. c, When using alternating helicity of the excitation pulses and detected signal, the system is driven into a coherent superposition between the K and K′ valley excitons during the delay t2. The width of the lineshape along ℏω2, shown by the slice in d, provides a measure of the valley coherence decay rate γv = 6.9 ± 0.2 meV.
We next probe the exciton valley coherence using a polarization scheme in which the first and third pulses are co-circularly polarized (σ+) and the second pulse and detected signal are co-circularly polarized but with opposite helicity (σ−). As illustrated in Fig. 2d, the first pulse creates a coherent superposition between the ground and exciton states in the K valley. After a time t1, the second pulse transfers this optical coherence to a coherent superposition between excitons in the K and K′ valleys, the evolution of which is monitored during the time t2. The third pulse converts the non-radiative valley coherence to an optical coherence of the K′ valley exciton, which is then detected. The corresponding 2D spectrum is shown in Fig. 3c. The spectrum features a single peak similar to the co-circular excitation sequence; however, the linewidth along ℏω2 is significantly wider, as illustrated by the lineshape shown in Fig. 3d. Because the system is in a coherent superposition of valley exciton states during t2, the HWHM linewidth along ℏω2 corresponds to the valley coherence decay rate γv. We measure γv = 6.9 ± 0.2 meV (τv = ℏ/γv = 98 ± 5 fs)—a factor of two faster than the population recombination rate.
To gain an in-depth understanding of possible processes responsible for exciton valley decoherence, we consider the Maialle–Silva–Sham mechanism—valley relaxation induced by the electron–hole exchange interaction24,25. In monolayer TMDs, the exciton valley DoF is intrinsically coupled to the exciton centre-of-mass motion by the exchange interaction (Fig. 4a). Exciton states in opposite valleys are degenerate at zero centre-of-mass momentum, but this two-fold valley degeneracy is lifted at finite momentum by the inter-valley exchange interaction, which acts as an in-plane effective magnetic field Ω coupled to the valley DoF (Fig. 4b). The magnitude of Ω scales linearly with the magnitude of the momentum, whereas the orientation of Ω rotates 4π when the momentum encloses its origin once. The interplay of intra- and inter-valley exchange interactions leads to unusual exciton dispersion36. As shown in Fig. 4a, the lower (upper) exciton band has quadratic (linear) dispersion with the exciton valley pseudospin antiparallel (parallel) to Ω.
a, Owing to inter-valley electron–hole exchange interaction, a bright exciton can be annihilated in valley K in company with the creation of a bright exciton in the opposite valley K′. b, Exciton valley bands in momentum space are illustrated. The electron–hole inter-valley exchange interaction acts as an effective magnetic field Ω that is responsible for relaxation of exciton valley coherence. The orientation of Ω depends on the exciton momentum Qx, y. c, When averaging over excitons distributed in momentum space, valley decoherence (solid lines) is faster than the population recombination lifetime N(t)/N(0) (dashed line). A larger exciton momentum scattering rate (1/τp) results in slower valley decoherence.
The time dynamics of the valley pseudospin vector is described by:

where Q denotes the centre-of-mass momentum. The first term on the right-hand side describes precession of S around the effective magnetic field Ω. The second term captures momentum scattering by a smooth impurity potential which changes the momentum of an exciton but does not act on spin or valley flavour. The last term in equation (1) phenomenologically accounts for scattering events that reduce the information carried by the valley DoF. We allow the rate ℏ/τ to differ for different components of S, and approximate that for Sz by ΓK and that for Sx, y by ΓK + 2γK∗, where γK∗ is the pure dephasing rate of optical coherence between the K-valley exciton and the ground state. We assume that S points initially along the x-direction, corresponding to coherence between exciton valley states generated by the first two circularly polarized pulses in the2DCS experiments.
In Fig. 4c the time evolution of the exciton population N, with the population decay rate taken from the co-circular 2DCS experiment, is plotted as the dashed line. The in-plane component averaged over momenta is illustrated by the solid lines in Fig. 4c, which represent coherence between the two valley exciton states. It is clear that the Maialle–Silva–Sham mechanism captures the experimental observations: the valley coherence decays faster than the population relaxes. This result can be understood by recognizing that the effective magnetic field Ω(Q) has a strong momentum dependence—thus, momenta averaging leads to decoherence. We also calculate a valley degree of circular polarization of ∼55% (see Supplementary Fig. 5), which suggests that a high degree of valley polarization is consistent with a short valley coherence time. The dependence of exciton valley coherence on the momentum scattering rate ℏ/τp, which is associated with the scattering strength W in equation (1), is also illustrated in Fig. 4c. Surprisingly, our calculations indicate that the larger ℏ/τp, the longer the valley coherence time. This counterintuitive behaviour is analogous to the motional narrowing effect seen in other solid-state and molecular systems37,38. When an exciton changes its momentum more frequently by impurity scattering, the time-averaged effective magnetic field it experiences is reduced. Quantitative agreement between the calculations and experiment is obtained for a momentum scattering rate ℏ/τp ≃ 10 meV. We note that impurity scattering enhances both the momentum scattering rate (ℏ/τp) and the exciton pure dephasing rate (γK∗), the latter of which suppresses the valley coherence time. Inter- and intravalley momentum scattering also leads to valley-dependent electronic spin precession and relaxation, as recently reported in monolayer MoS2 and WS2—analogous to spin depolarization commonly found in conventional semiconductors and graphene39,40,41. Interestingly, additional 2DCS measurements at elevated temperatures reveal that the valley coherence decay rate γv increases to 7.5 ± 0.2 meV at 30 K, whereas the population recombination rate ΓK remains unchanged within the estimated uncertainty (data not shown). This weak temperature dependence suggests that acoustic phonon scattering plays a small role in exciton valley decoherence, and is additional evidence that the electron–hole exchange interaction provides an efficient valley decoherence mechanism.
The experimental and theoretical results presented here offer critical insight into valley decoherence mechanisms. Such information also provides important guidance for implementing valleytronics based on TMDs, because all coherent manipulations of the exciton valley pseudospin have to be performed before coherence is lost. Several important messages regarding valley physics in monolayer TMD emerge from this work. First, understanding the mechanisms limiting the exciton population lifetime is of utmost importance, as exciton recombination places an upper bound on the valley coherence time. Second, impurity scattering introduces competing effects on exciton valley coherence. Although certain types of impurities may lead to non-radiative recombination and shorten the population lifetime, impurity scattering can also enhance coherence by effectively screening the exchange interaction. Finally, in our experiments we resonantly excite excitons confined within a single monolayer, which are expected to exhibit intrinsic rapid radiative decay at cryogenic temperatures42. Extending the exciton valley coherence time might be possible through resonant optical excitation of other exciton-type states. For example, strongly localized quantum-dot-like exciton states43,44 in monolayers and indirect excitons in multi-layer heterostructures45 couple more weakly with the optical field, and thus exhibit a longer population lifetime. Exciting these states may allow for coherent control of the valley pseudospin DoF over a longer duration. Alternatively, embedding TMDs in photonic cavities creates hybrid exciton-polariton states with lifetimes that can be tuned by controlling the exciton–photon coupling parameter46. These advanced materials and photonic structures are likely to offer additional flexibility in controlling the valley DoF.
Methods
Sample preparation and characterization.
The monolayer WSe2 sample was grown using chemical vapour deposition, as described in detail in ref. 27 and Supplementary Note 1. Briefly, the sample was synthesized on a double-side-polished sapphire substrate for transmission optical spectroscopy experiments. We verified the monolayer thickness using atomic force microscopy. The sample is mounted in a liquid helium cold-finger cryostat and held at a temperature of 10 K. The photoluminescence experiments were performed using a continuous wave laser at 660 nm, which was focused to a spot size of ∼2 μm in diameter. The photoluminescence spectra in Fig. 2a were fitted with double Gaussian functions to determine the degree of circular polarization.
Two-dimensional coherent spectroscopy.
100-fs pulses generated from a mode-locked Ti:sapphire laser at a repetition rate of 80 MHz are split into a set of four phase-stabilized pulses. Three of the pulses are focused to an overlapped 35 μm FWHM spot on the sample, which probably probes a few monolayer flakes. The coherent interaction of the three fields with the sample generates a third-order nonlinear optical signal field, ES(t1, t2, t3), which is a photon echo (or four-wave mixing signal) detected in transmission in the wavevector-matching direction. ES is interferometrically measured by means of heterodyne detection with a fourth phase-stabilized reference field ER. Both phase and amplitude of ES as a function of emission energy ℏω3 are extracted from the spectral interferograms of ES and ER obtained using a spectrometer. Subsequent Fourier transformation of the signal field with respect to the delay t2 yields a rephasing ‘zero-quantum’ spectrum with amplitude given by ES(t1, ℏω2, ℏω3). We use a value of t1 = 0 fs to obtain maximum signal to noise; however, using a value of t1 = 100 fs, which is larger than the pulse duration, provides similar results, apart from an overall smaller signal amplitude.
Extraction of coherence and relaxation times.
Different relaxation times can be extracted by scanning different delays and choosing different polarization for the excitation pulses. If all four pulses are co-circularly polarized, σ+σ+σ+σ+, we are addressing excitons in only one valley. By scanning the delay t1 between the first two pulses, we extract the exciton dephasing time (see ref. 34). Experiments based on this choice of polarization and delay scan (t1) are similar to the self-diffracted four-wave mixing experiments. If the delay t2 between the second and third pulses is scanned as shown in Fig. 3, one can extract the exciton population relaxation time. Our experiment based on this choice of polarization and delay scan t2 is analogous to the familiar pump–probe technique. Finally, if we choose σ+σ−σ+σ− and scan the delay t2 between the second and third pulses, we extract the valley decoherence time. We present the relaxation and decoherence dynamics in the spectral domain, where the HWHM of the spectral lineshapes is inversely proportional to the time-domain decay rates (see ref. 35 for details).
References
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. Valleytronics. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014).
Xiao, D., Liu, G.-B., Feng, W., Xu, X. & Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other Group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Yu, H., Liu, G.-B., Gong, P., Xu, X. & Yao, W. Dirac cones and Dirac saddle points of bright excitons in monolayer transition metal dichalcogenides. Nature Commun. 5, 3876 (2014).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nature Phys. 10, 343–350 (2014).
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl Acad. Sci. USA 102, 10451–10453 (2005).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2 . Nano Lett. 10, 1271–1275 (2010).
Jones, A. M. et al. Optical generation of excitonic valley coherence in monolayer WSe2 . Nature Nanotech. 8, 634–638 (2013).
Wang, G. et al. Giant enhancement of the optical second-harmonic emission of WSe2 monolayers by laser excitation at exciton resonances. Phys. Rev. Lett. 114, 097403 (2015).
Chernikov, A. et al. Exciton binding energy and nonhydrogenic Rydberg series in monolayer WS2 . Phys. Rev. Lett. 113, 076802 (2014).
Zhu, B., Chen, X. & Cui, X. Exciton binding energy of monolayer WS2 . Sci. Rep. 5, 9218 (2015).
Ugeda, M. M. et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nature Mater. 13, 1091–1095 (2014).
Cao, T. et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nature Commun. 3, 887 (2012).
Korn, T., Heydrich, S., Hirmer, M., Schmutzler, J. & Schuller, C. Low-temperature photocarrier dynamics in monolayer MoS2 . Appl. Phys. Lett. 99, 102109 (2011).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nature Nanotech. 7, 494–498 (2012).
Shi, H. et al. Exciton dynamics in suspended monolayer and few-layer MoS2 2D crystals. ACS Nano 7, 1072–1080 (2013).
Wang, G. et al. Valley dynamics probed through charged and neutral exciton emission in monolayer WSe2 . Phys. Rev. B 90, 075413 (2014).
Wang, Q. et al. Valley carrier dynamics in monolayer molybdenum disulfide from helicity-resolved ultrafast pump–probe spectroscopy. ACS Nano 7, 11087–11093 (2013).
Zeng, H., Dai, J., Yao, W., Xiao, D. & Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nature Nanotech. 7, 490–493 (2012).
Lagarde, D. et al. Carrier and polarization dynamics in monolayer MoS2 . Phys. Rev. Lett. 112, 047401 (2014).
Mai, C. et al. Many-body effects in valleytronics: direct measurement of valley lifetimes in single-layer MoS2 . Nano Lett. 14, 202–206 (2014).
Yu, H., Cui, X., Xu, X. & Yao, W. Valley excitons in two-dimensional semiconductors. Natl Sci. Rev. 2, 57–70 (2015).
Cundiff, S. T. et al. Optical 2-D Fourier transform spectroscopy of excitons in semiconductor nanostructures. IEEE J. Sel. Top. Quantum Electron. 18, 318–328 (2012).
Maialle, M. Z., de Andrada E Silva, E. A. & Sham, L. J. Exciton spin dynamics in quantum wells. Phys. Rev. B 47, 15776–15788 (1993).
Vinattieri, A. et al. Exciton dynamics in GaAs quantum wells under resonant excitation. Phys. Rev. B 50, 10868–10879 (1994).
Yu, T. & Wu, M. W. Valley depolarization due to intervalley and intravalley electron–hole exchange interactions in monolayer MoS2 . Phys. Rev. B 89, 205303 (2014).
Huang, J.-K. et al. Large-area synthesis of highly crystalline WSe2 monolayers and device applications. ACS Nano 8, 923–930 (2013).
Boller, K.-J., Imamoglu, A. & Harris, S. E. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 66, 2593–2596 (1991).
Scully, M. O., Zhu, S.-Y. & Gavrielides, A. Degenerate quantum-beat laser: lasing without inversion and inversion without lasing. Phys. Rev. Lett. 62, 2813–2816 (1989).
Zibrov, A. S. et al. Experimental demonstration of laser oscillation without population inversion via quantum interference in Rb. Phys. Rev. Lett. 75, 1499–1502 (1995).
Gobel, E. O. et al. Quantum beats of excitons in quantum wells. Phys. Rev. Lett. 64, 1801–1804 (1990).
Lenihan, A. S., Gurudev Dutt, M. V., Steel, D. G., Ghosh, S. & Bhattacharya, P. K. Raman coherence beats from entangled polarization eigenstates in InAs quantum dots. Phys. Rev. Lett. 88, 223601 (2002).
Bristow, A. D. et al. A versatile ultrastable platform for optical multidimensional Fourier-transform spectroscopy. Rev. Sci. Instrum. 80, 073108 (2009).
Moody, G. et al. Intrinsic homogeneous linewidth and broadening mechanisms of excitons in monolayer transition metal dichalcogenides. Nature Commun. 6, 8315 (2015).
Siemens, M. E., Moody, G., Li, H., Bristow, A. D. & Cundiff, S. T. Resonance lineshapes in two-dimensional Fourier transform spectroscopy. Opt. Express 18, 17699–17708 (2010).
Wu, F., Qu, F. & MacDonald, A. H. Exciton band structure in monolayer MoS2 . Phys. Rev. B 91, 075310 (2015).
Oxtoby, D. W. Hydrodynamic theory for vibrational dephasing in liquids. J. Chem. Phys. 70, 2605–2610 (1979).
Berthelot, A. et al. Unconventional motional narrowing in the optical spectrum of a semiconductor quantum dot. Nature Phys. 2, 759–764 (2006).
Li, P., Li, J., Qing, L., Dery, H. & Appelbaum, I. Anisotropy-driven spin relaxation in germanium. Phys. Rev. Lett. 111, 257204 (2013).
Yang, L. et al. Long-lived nanosecond spin relaxation and spin coherence of electrons in monolayer MoS2 and WS2 . Nature Phys. 11, 830–834 (2015).
Van Tuan, D., Ortmann, F., Soriano, D., Valenzuela, S. O. & Roche, S. Pseudospin-driven spin relaxation mechanism in graphene. Nature Phys. 10, 857–863 (2014).
Palummo, M., Bernardi, M. & Grossman, J. C. Exciton radiative lifetimes in two-dimensional transition metal dichalcogenides. Nano Lett. 15, 2794–2800 (2015).
Srivastava, A. et al. Optically active quantum dots in monolayer WSe2 . Nature Nanotech. 10, 491–496 (2015).
Koperski, M. et al. Single photon emitters in exfoliated WSe2 structures. Nature Nanotech. 10, 503–506 (2015).
Rivera, P. et al. Observation of long-live interlayer excitons in monolayer MoSe2–WSe2 heterostructures. Nature Commun. 6, 6242 (2015).
Liu, X. et al. Strong light-matter coupling in two-dimensional atomic crystals. Nature Photon. 9, 30–34 (2015).
Acknowledgements
The theoretical and experimental collaboration is made possible by SHINES, an Energy Frontier Research Center funded by the US Department of Energy (DoE), Office of Science, Basic Energy Science (BES) under award # DE-SC0012670. K.H., F.W., L.X., X.L. and A.H.M. have all received support from SHINES. Optical spectroscopy studies performed by K.H., C.K.D., L.S. and X.L. have been partially supported by NSF DMR-1306878 and Welch Foundation F-1662. A.H.M. also acknowledges support from Welch Foundation F-1473. L.J.L. is grateful for support from KAUST Saudi Arabia, Academia Sinica Taiwan, and AOARD FA23861510001 USA. C.-H.C. is grateful for support from the Ministry of Science and Technology Taiwan (MOST 104-2218-E-035-010 and 104-2628-E-035-002-MY3).
Author information
Authors and Affiliations
Contributions
K.H. and G.M. contributed equally to this work. G.M. and X.L. conceived the concept. K.H. led the experimental effort. All co-authors at the University of Texas ran the experiments, acquired the data, and analysed the results. C.-H.C., M.-Y.L. and L.-J.L. provided the samples. F.W. and A.H.M. performed the theoretical studies. G.M., F.W. and X.L. wrote the manuscript. All authors discussed the results and commented on the manuscript at all stages.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1070 kb)
Rights and permissions
About this article
Cite this article
Hao, K., Moody, G., Wu, F. et al. Direct measurement of exciton valley coherence in monolayer WSe2. Nature Phys 12, 677–682 (2016). https://doi.org/10.1038/nphys3674
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3674
This article is cited by
-
Optical two-dimensional coherent spectroscopy of excitons in transition-metal dichalcogenides
Frontiers of Physics (2024)
-
Observation of ~100% valley-coherent excitons in monolayer MoS2 through giant enhancement of valley coherence time
Light: Science & Applications (2023)
-
Zero-field quantum beats and spin decoherence mechanisms in CsPbBr3 perovskite nanocrystals
Nature Communications (2023)
-
p-Type Two-Dimensional Semiconductors: From Materials Preparation to Electronic Applications
Nano-Micro Letters (2023)
-
Interlayer exciton formation, relaxation, and transport in TMD van der Waals heterostructures
Light: Science & Applications (2021)