Abstract
Quantum entanglement emerges naturally in interacting quantum systems and plays a central role in quantum information processing1,2,3,4. But the generation of entanglement does not require direct interactions: single-photon detection in spin-flip Raman scattering projects two distant spins onto a maximally entangled state, provided that it is impossible to determine the source of the detected photon5. Here, we demonstrate such heralded quantum entanglement6,7,8,9 of two quantum-dot hole spins separated by 5 m using single-photon interference. Thanks to fast spin initialization in 10 ns, hole-spin coherence lasting ∼40 ns and efficient photon extraction from dots10,11,12 embedded in leaky microcavity structures, we generate 2,300 entangled spin pairs per second, which represents a 1,000-fold improvement as compared to previous experiments13. The delayed two-photon interference scheme we developed allows the efficient verification of quantum correlations. Combined with schemes for transferring quantum information to a long-lived memory qubit14, fast entanglement generation could impact quantum repeater architectures.
Similar content being viewed by others
Main
In contrast to previous experiments demonstrating electron spin photon entanglement 10,11,12, our experiments are based on heavy-hole pseudo-spins in self-assembled quantum dots (QD) that have been shown to exhibit long coherence times15,16,17,18. Figure 1a depicts our experimental set-up, incorporating two QDs separated by 5 m that are resonantly driven by weak 3.2 ns-long pulses from a Ti:Sapphire laser, termed the entanglement laser. Additional diode laser pulses ensure that each QD is optically charged with a single excess heavy hole and that the hole pseudo-spin is prepared in the requisite state. The QDs are embedded in distributed Bragg reflector (DBR) structures19 which, together with a ZnO solid immersion lens, allow efficient (∼20%) collection of the generated resonance fluorescence.
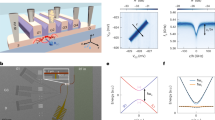
a, Two bath cryostats separated by 5 m host quantum-dot samples in Voigt geometry. The quantum dots can be addressed by diode lasers (in black) for local state preparation and readout, and by a Ti:Sapphire laser (in blue) for entanglement generation and non-local measurement. EOM stands for electro-optic modulator. b, Energy-level diagram of a single quantum dot. On excitation of the neutral exciton (|X0〉) state, the electron can tunnel out, leaving behind a single hole. Application of a finite magnetic field gives rise to spin-dependent optical selection rules with four allowed transitions of identical oscillator strength. c, Characterization of the indistinguishability of the Raman photons from the two dots with a Hong–Ou–Mandel experiment: coincidence counts on the two output arms of BS2 are plotted as a function of the delay between the recorded photon arrival times under pulsed excitation. T0 is the repetition period of 52 ns. When the input modes have parallel polarizations (red curve), the coincidence counts within the time window (−1 ns, 1 ns) are 11 times smaller than for the case of the input modes having orthogonal polarization.
Figure 1b shows the relevant energy-level diagram as well as the allowed optical transitions for single-hole charged QDs when an external magnetic field (Bx) is applied perpendicular to the growth direction (Voigt geometry; refs 20,21). The initial states of the optical transitions in the single-hole charged regime are metastable states identified by the orientation of the heavy-hole pseudo-spin, with |⇑〉 (|⇓〉) denoting +3/2 (−3/2) hole angular momentum projection. The presence of Bx ≠ 0 yields a finite splitting of the pseudo-spin states due to heavy–light hole mixing22. Spontaneous emission of a V (H) polarized photon at frequency ωblue (ωdiag1) from the trion state |Tb〉 at rate Γ/2 brings the QD back into the |⇓〉 (|⇑〉) state. Owing to these selection rules, addressing any of the four allowed transitions with a single laser will efficiently transfer the spin population into the opposite ground state within 10 ns (see Supplementary information). As the intensity of the entanglement laser is chosen to be well below saturation, the ensuing optical transitions lead to either V-polarized Rayleigh scattering or H-polarized Raman scattering. The spin-flip associated with the generation of a Raman photon precludes emission of two or more Raman photons during the same pulse.
The light propagation times from the first beamsplitter (BS1) to both dots, as well as from the dots to the second beamsplitter (BS2), are rendered nearly identical, such that the photons scattered by the two dots during a single entanglement laser pulse reach the second beamsplitter at the same time. When both QDs are initially prepared in the |⇓〉 state, the simultaneous weak excitation of the blue transitions will lead to either a Raman or Rayleigh scattering event with a probability ɛ2 ≪ 1, leaving the system in the state

where |1b,H〉 refers to a single H-polarized photon with centre frequency ωblue and |1d1,V〉 refers to a single V-polarized photon with centre frequency ωdiag1. To ensure that a click in one of the single-photon detectors stems from Raman scattering we use polarizers, transmission gratings and Fabry–Pérot filters (see Methods). In this case, detection of a single (Raman) photon projects the composite system wavefunction onto the maximally entangled state

in the limit where the two-photon scattering probability ɛ4 is vanishingly small. Provided that the Zeeman splitting in the two QDs are rendered identical, the relative phase θ = θ2 − θ1 is independent of time and is primarily determined by the optical path-length difference between the two arms from BS1 to BS2 (Fig. 1a).
The entanglement generation scheme we use relies crucially on the indistinguishability of the photons emitted by two remote QDs (QD1 and QD2) such that ‘which-path’ information is not available in the single-photon interferometer depicted in Fig. 1a. The indistinguishability of the Raman-scattered photons is characterized by a Hong–Ou–Mandel (HOM) experiment23 (see Methods). Figure 1c shows that two-photon interference results in a strong decrease of the twofold coincidence rate associated with the central peak when the two input photons have parallel polarizations. The associated interference visibility deduced from this measurement is 91 ± 6%, guaranteeing that no substantial ‘which-path’ information is conveyed by Raman photons.
For the protocol we implement, it is essential that the QD spins remain coherent during the time it takes for the heralding process to be completed. In our scheme the latter is determined predominantly by the 21.7 ns propagation time from the QDs to the single-photon detectors. To demonstrate that the hole pseudo-spin retains its coherence on this timescale, we implemented a quantum optical measurement technique. It is well known in quantum optics that whereas the first-order coherence properties of Rayleigh scattering follow that of the excitation laser24,25, the coherence of spin-flip Raman scattering is determined both by the laser and the spin coherence26. The latter is a consequence of the fact that the quantum field E(+)(t) generated in Raman scattering is linearly proportional to the spin-raising operator σ⇑⇓(t − R/c), where R denotes the distance between the QD and the detector. Therefore, the hole-spin coherence (T2∗) time can be determined by measuring the coherence time of Raman-scattered photons, provided that the excitation laser has a much longer coherence time.
To perform this experiment, we use the set-up depicted in Fig. 2a, where the emitted photons at a desired wavelength are filtered and then sent into a stabilized Mach–Zehnder interferometer whose path-length difference is set to 22 ns. Using the pulse sequence depicted in Fig. 2b (see Methods), we obtain for Raman photons an interference visibility of 38.9 ± 1.9% for QD1 and 29.5 ± 2.9% for QD2, which is more than half the visibility measured for Rayleigh scattering (66.7 ± 1.7% for QD1 and 54.8 ± 2.5% for QD2). The visibility of Rayleigh photons is limited by a contribution from incoherent light scattering, whereas Raman coherence is in addition reduced by the decay of spin coherence. This result demonstrates that both spins have a coherence time longer than 22 ns.
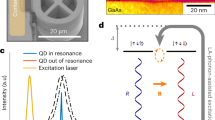
a, Sketch of the experimental set-up for the single-photon interference of Raman-scattered photons. The single photons are sent to an interferometrically stabilized Mach–Zehnder (MZ) interferometer of path-length difference cΔt. A single-photon detector is placed in one of the output modes of the second beamsplitter. b, Pulse sequence used for the first-order coherence measurement, and the relevant energy-level diagram. We first apply a pulse of frequency ωred to spin pump into the |⇓〉 state (pulse 1). We then apply two successive weak pulses (2 and 3) at frequency ωblue. The time offset of the two pulses approximately matches the path-length difference of the MZ interferometer. c, Count rate of the single-photon detector, for QD1 (left column) and QD2 (right column), when filtering only the Raman-scattered (upper row) or the Rayleigh-scattered (lower row) photons, as a function of the phase difference in the two arms. The associated visibility, obtained from a sinusoidal fit of the count rate, is indicated in the associated panel. d, Pulse sequence used to demonstrate pseudo-spin rotation about the z axis of the Bloch sphere: the pulse sequence is identical to the one used for part (B), with an additional detuned laser pulse of 4 ns (pulse 3) inserted in between the two pulses at ωblue (2 and 4). e, Black dots: count rate of the output detector, as a function of the detuned laser power, demonstrating control of the pseudo-spin phase. Red curve: fit to the data. The error bars of the visibilities correspond to 1 s.d.
The fringes in the aforementioned Mach–Zehnder interferometer could also be observed by varying the phase of the hole pseudo-spin. The latter can be adjusted using a V-polarized off-resonant laser field that induces different phases on the two spin states due to different magnitudes of the ac-Stark effect. We carried out this experiment on QD1 by applying a laser that is red-detuned by ∼20 GHz from the red and ∼50 GHz from the blue vertical transition (bottom right diagram of Fig. 2d). The difference in the ac-Stark shift experienced by the two transitions allows the state |⇓〉 to accumulate a phase ϕ = Ω2τδ/4Δ(Δ + δ), relative to |⇑〉. Here, Ω is the Rabi frequency of the laser, τ the pulse duration, Δ the detuning from the red transition and δ = ωblue − ωred the energy difference between the two transitions. To characterize the effect of spin-phase rotation, we repeat the interferometric measurement while keeping the optical path-length difference constant and applying a 4 ns-long detuned laser pulse in between the two weak excitation pulses (Fig. 2d). By varying the laser power from 0 to ∼2 μW, we change the relative phase of the two spin states, and thus the relative phase of the Raman scattering amplitude before and after the pulse that induces the spin-state-dependent ac-Stark shift. The oscillations in the count rate as a function of the laser power (Fig. 2e, black dots) unequivocally demonstrate single pseudo-spin rotation about the z axis of the Bloch sphere. The red curve in Fig. 2e is a sinusoidal fit to the data, showing that no sizeable loss of visibility is observed for spin rotation up to 4π.
To demonstrate classical correlations between the distant spins, we carry out local single-spin measurement in the computational basis, conditioned on the detection of a Raman photon during the entanglement pulse. We benefit from the fact that each spin state can be excited to a corresponding trion state with the same oscillator strength and the same laser polarization, but using a different resonant laser wavelength. The detection of a photon during a blue (red) laser pulse thus tells with a high confidence level that the state of the spin before the measurement pulse was |⇓〉 (|⇑〉). To measure the four different spin combinations under the same experimental conditions, we alternate in a single experiment four pulse sequences, each performing one of the four requisite measurement combinations. The full pulse sequence is described in Fig. 3a: we first prepare the state |⇓, ⇓〉 by spin pumping, then apply the weak entanglement laser pulse. The power used is ∼2% of the saturation power and the Raman photon scattering probability is ɛ2 ∼ 7%. The detection of a Raman photon during this pulse heralds successful entanglement generation. We then successively measure the state of the two dots. The measurement pulses of the two dots are offset in time, allowing us to extract which-path information. These two measurements are performed close to saturation and the detection efficiencies are rendered similar. The duration of the full sequence is 4 × 104 ns. Figure 3b shows the results of the threefold coincidences detected during 106.5 h of measurement. As expected, the odd-parity events, where the spins of the two dots are opposite, are much more likely than the even-parity events, where the two spins are found in the same state. The associated fidelity is Fz = 80.6 ± 6.6%.
a, Pulse sequence used for the measurement of classical correlations between the distant spins. After spin pumping into the |⇓, ⇓〉 state (pulse 1), a weak entanglement pulse (pulse 2) is sent simultaneously to both quantum dots (QD1 and QD2). After 22 ns, pulse 3 measures the spin state of QD1 and then pulse 4 measures the spin state of QD2. The four measurement combinations are alternated. The total repetition period of the measurement processes is 4 × 104 ns. b, Red bars: results of threefold coincidences between a photon emitted during the entanglement pulse and a photon in each of the two measurement pulses (orange shading in a) obtained during a total measurement time span of 106.5 h. The dashed bars represents the ideal limit of vanishing even-parity spin-state detection. The error bars represent 1 s.d. deduced from Poissonian statistics of the raw detection events. The measured fidelity is Fz = 80.6 ± 6.6%. c, Pulse sequence used to measure quantum correlations between the distant spins. After spin pumping into the |⇓, ⇓〉 state, a weak entanglement pulse (pulse 2) is used to drive both quantum dots. A detuned laser pulse (pulse 3) modifies the phase of the QD1 hole-spin phase. After 22 ns, a non-local measurement pulse is applied to both QDs. The pulse sequence is repeated for different values of the duration of pulse 3 ranging from 0 to 8 × 0.82 ns, corresponding to a laser-induced QD1 spin-phase rotation ranging from 0 to 3π. d, Black dots: twofold coincidence rate between a photon detected during the entanglement pulse and a second photon detected during the measurement pulse (orange shading in c), normalized by the average detection rate between photons emitted during different periods, as a function of the length of pulse 3. The error bars represent 1 s.d. deduced from Poissonian statistics of the raw detection events. The red curve is a sinusoidal fit to the data, yielding a visibility of V = 29.8 ± 2.6%, where the error bar corresponds to 1 s.d. The deduced overall fidelity is F = (Fz + V)/2 = 55.2 ± 3.5%, where the error bar is deduced from that of Fz and V by the Gauss error propagation law for independent measurement uncertainties.
To demonstrate quantum correlations between the two distant spins, we implement a delayed two-photon interference experiment. The key element of this approach for verifying quantum correlations is the possibility to rotate one of the spins along the z-axis after heralded spin entanglement is generated. Application of a detuned laser pulse on QD1, as described earlier, results in rotating the phase of the entangled state by α(τ) so that the entangled state becomes  . Subsequent application of a second weak (measurement) pulse, that is identical in intensity and duration to the entanglement pulse, on both QDs simultaneously leads to
. Subsequent application of a second weak (measurement) pulse, that is identical in intensity and duration to the entanglement pulse, on both QDs simultaneously leads to


Therefore, conditioned on an initial Raman photon detection event that heralded spin–spin entanglement, the detection of a second time-delayed Raman photon detection probability scales as ɛ2|1 + e−iα(τ)|2. The expectation value of Raman photon detection can be shown to be

The peak-to-peak contrast in 〈E(−)E(+)〉 obtained by varying α(τ) therefore gives us the magnitude of non-local quantum correlations between the two spins (see Supplementary Information).
To verify the presence of quantum correlations using such a delayed two-photon interference experiment, we use the pulse sequence described in Fig. 3c. We once again prepare the spins in the |⇓, ⇓〉 state by spin pumping and then apply the weak entanglement generation pulse in the same way as for the classical correlation measurement. The phase of the state is then modified by the detuned laser pulse, whose duration is changed within the pulse sequence by alternating eight patterns that differ only by the duration of this particular pulse. Eight evenly distributed durations are chosen to cover more than one full revolution. Finally, the measurement pulse is simultaneously sent to both dots. The duration of the full sequence is 8 × 52 ns. The twofold coincidences measured for each value of the pulse length are normalized by the uncorrelated coincidence rate obtained by measuring two photons emitted in different periods. Figure 3d presents data obtained during 180 min of measurement. The obtained ratio exhibits clear oscillations of visibility 29.6 ± 2.8%. Combining the results depicted in Fig. 3b and d, we deduce an overall fidelity of the generated entangled state of F = 55.2 ± 3.5% (see Supplementary Information). Although this number is relatively modest compared to previous work based on other physical systems6,7,8,13,27, it is predominantly limited by the T2∗ coherence time of the hole spins, and hence could be substantially increased by the introduction of dynamical decoupling16. The data depicted in Fig. 3d are obtained when the detection rate of single photons emitted during the entanglement pulse is 2,300 photons per second; the latter directly yields the heralded entanglement generation rate. Such a high generation rate was possible thanks to the fast spin initialization (10 ns) allowing us to use a high repetition rate (Γrep = 1.9 × 107 s−1) and a relatively high photon collection efficiency of ∼20% to the objective, ensuring an overall collection efficiency of ∼0.2% (see Supplementary Information).
The non-local measurement of quantum correlations does not allow us to determine the relative phase θ between the |⇑⇓〉 and |⇓⇑〉 contributions. In the ideal limit of z-basis measurements yielding vanishing probability for |⇑⇑〉 and |⇓⇓〉 states, the state space of the two qubits is restricted to a two-dimensional subspace which can be mapped onto a Bloch sphere with |⇑⇓〉 and |⇓⇑〉 as the north and the south poles, respectively. A perfect visibility in non-local two-photon interference in return ensures that the two-spin state lives on the equator of this Bloch sphere:  . To fix the value of θ, we need to use a strong laser to stabilize the optical path-length difference to an integer multiple of its wavelength immediately before the generation of the entangled spin state. We have implemented such a stabilization scheme (see Supplementary Information) to perform the Mach–Zehnder interferometry measurements depicted in Fig. 2. We emphasize that it is straightforward to extend our heralded entanglement generation experiments by fixing θ with an accuracy of ± π/10 using this stabilization scheme while achieving nearly the same entanglement generation rate.
. To fix the value of θ, we need to use a strong laser to stabilize the optical path-length difference to an integer multiple of its wavelength immediately before the generation of the entangled spin state. We have implemented such a stabilization scheme (see Supplementary Information) to perform the Mach–Zehnder interferometry measurements depicted in Fig. 2. We emphasize that it is straightforward to extend our heralded entanglement generation experiments by fixing θ with an accuracy of ± π/10 using this stabilization scheme while achieving nearly the same entanglement generation rate.
The improvement of the entanglement generation rate by almost three orders of magnitude is enabled by the favourable properties of semiconductor quantum emitters, ensuring a fast spin-state initialization and a high emission rate of indistinguishable single photons associated with integrated cavity structures, ensuring efficient light extraction. The observed rate could be further increased by a factor of ten using cavity-QED (ref. 19). The relatively long T2∗ coherence times of the hole spins were essential for the demonstration of entanglement of spins that are 5 m apart. Increasing the distance between the entangled spin pairs could be achieved either by using dynamical decoupling or by using singlet–triplet qubits of QD molecules that exhibit longer spin coherence times while simultaneously allowing efficient spin measurement28. Our results provide a strong motivation for investigating possibilities for coherent transfer of the hole spin to a local qubit that exhibits a longer coherence time14 but lacks an efficient interface to propagating optical photons27. A hybrid system that uses QD spins for fast entanglement generation and long-lived qubits for storage could have a significant impact on the implementation of quantum repeaters3. In addition, heralded spin entanglement could provide a quantum coherent link between nodes of an on-chip quantum information processor29,30.
Methods
Experimental set-up.
The samples are inserted in two cryostats operating at liquid helium temperature and separated by 5 m. In both cryostats, a fibre-coupled confocal microscope focuses the excitation laser pulses onto the QD using a high NA (0.65) objective. The QD emission is collected through the same objective and coupled into a collection fibre. A polarizer is placed at the input port of each cryostat such that the QDs are driven with vertically polarized light. To suppress the reflected laser background, another polarizer with an orthogonal orientation is placed at the output port; as a consequence only horizontally polarized scattered photons are detected.
All the laser pulses are obtained from cw lasers by electro-optical modulators with a 103 on/off ratio. The pulses are generated by synchronized pulse pattern generators of jitter < 10 ps. For the quantum correlation measurements, the two output ports of the second beamsplitter (BS2) are fed into two identical avalanche photo-diodes with 350 ps jitter and quantum efficiency 25%. For the classical correlation measurement, one of the output ports of BS2 is fed into an avalanche photodiode (which is gated during the entanglement pulse) and the other port is split once more and fed into two superconducting single-photon detectors (SSPDs) of 65 ps jitter and quantum efficiency 40% (which are gated during the measurement pulses). To select the relevant wavelength, Fabry–Perot (FP) filters and gratings are inserted just after BS2. The Fabry–Perot filters are silica plates of 1 mm thickness, 1.7 GHz bandwidth and 90% transmission probability at peak wavelength; the gratings are fused silica blazed gratings of 1,500 l mm−1 and 95% transmittance. A time-correlated single-photon counting module (TCSPC) is used to record the photon detection events, allowing computer-based post-selection and processing of time-tagged photon records. For the single-photon interference experiments described in Fig. 2, the detector is gated in real time using a commercial ultra-fast digital electronic gate at the output port of the single-photon detector.
Indistinguishability of Raman photons.
The entanglement protocol requires that both optical transition frequencies ωblue and ωdiag1 are identical for QD1 and QD2. This condition is obtained by first locating a pair of QDs with similar transition energies using photoluminescence spectroscopy, then tuning both electric and magnetic fields applied on the two QDs separately. The indistinguishability of the Raman photons scattered by the two dots is characterized in a Hong–Ou–Mandel experiment under pulsed excitation of the blue transition using the set-up depicted in Fig. 1. We monitor the coincidence events at the two single-photon detectors after having filtered only the photons of centre frequency ωdiag1.
Mach–Zehnder interferometry of Raman photons.
The experiment is performed using the pulse sequence shown in Fig. 2b, where the spin is first prepared in the |⇓〉 state by spin pumping using the red (vertical) transition. We then apply two weak pulses on the blue transition, separated by a time offset that approximately matches the path-length difference, such that the light scattering amplitudes during the two pulses can interfere at the second beamsplitter. The detector is then gated so that it measures only in this interference time window and the photon detection events are recorded as a function of the phase difference between the two arms (see Supplementary Information). As a reference, we measure an interference visibility of 83 ± 1.8% for the excitation laser, limited by the precision with which we stabilize the optical path-length difference.
References
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Childress, L., Taylor, J. M., Sørensen, A. S. & Lukin, M. D. Fault-tolerant quantum communication based on solid-state photon emitters. Phys. Rev. Lett. 96, 070504 (2006).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Cabrillo, C., Cirac, J. I., García-Fernández, P. & Zoller, P. Creation of entangled states of distant atoms by interference. Phys. Rev. A 59, 1025–1033 (1999).
Moehring, D. L. et al. Entanglement of single-atom quantum bits at a distance. Nature 449, 68–71 (2007).
Hofmann, J. et al. Heralded entanglement between widely separated atoms. Science 337, 72–75 (2012).
Slodicka, L. et al. Atom-atom entanglement by single-photon detection. Phys. Rev. Lett. 110, 083603 (2013).
Bernien, H. et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 497, 86–90 (2013).
Gao, W. B., Fallahi, P., Togan, E., Miguel-Sanchez, J. & Imamoğlu, A. et al. Observation of entanglement between a quantum dot spin and a single photon. Nature 491, 426–430 (2012).
De Greve, K. et al. Quantum-dot spin-photon entanglement via frequency downconversion to telecom wavelength. Nature 491, 421–425 (2012).
Shaibley, J. R. et al. Demonstration of quantum entanglement between a single electron spin confined to an InAs quantum dot and a photon. Phys. Rev. Lett. 110, 167401 (2013).
Hucul, D. et al. Modular entanglement of atomic qubits using photons and phonons. Nature Phys. 11, 37–42 (2015).
Meyer, H. M. et al. Direct photonic coupling of a semiconductor quantum dot and a trapped ion. Phys. Rev. Lett. 114, 123001 (2015).
Brunner, D. et al. A coherent single-hole spin in a semiconductor. Science 325, 70–72 (2009).
De Greve, K. et al. Ultrafast coherent control and suppressed nuclear feedback of a single quantum dot hole qubit. Nature Phys. 7, 872–878 (2011).
Greilich, K., Carter, S. G., Kim, D., Bracker, A. S. & Gammon, D. Optical control of one and two hole spins in interacting quantum dots. Nature Photon. 5, 702–708 (2011).
Carter, S. G. et al. Strong hyperfine-induced modulation of an optically driven hole spin in an InAs quantum dot. Phys. Rev. B 89, 075316 (2014).
Gazzano, O. et al. Bright solid-state sources of indistinguishable single photons. Nature Commun. 4, 1425 (2013).
Xu, X. et al. Fast spin state initialization in a singly charged InAs-GaAs quantum dot by optical cooling. Phys. Rev. Lett. 99, 097401 (2007).
Atatüre, M. et al. Quantum-dot spin-state preparation with near-unity fidelity. Science 312, 551–553 (2006).
Bayer, M. et al. Fine structure of neutral and charged excitons in self-assembled In(Ga)As/(Al)GaAs quantum dots. Phys. Rev. B 65, 195315 (2002).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Loudon, R. The Quantum Theory of Light (Oxford Univ. Press, 2000).
Matthiesen, C., Vamivakas, A. N. & Atatüre, M. Subnatural linewidth single photons from a quantum dot. Phys. Rev. Lett. 108, 093602 (2012).
Fernandez, G., Volz, T., Desbuquois, R., Badolato, A. & Imamoğlu, A. Optically tunable spontaneous Raman fluorescence from a single self-assembled InGaAs quantum dot. Phys. Rev. Lett. 103, 087406 (2009).
Robledo, L. et al. High-fidelity projective read-out of a solid-state spin quantum register. Nature 477, 574–578 (2011).
Weiss, K. M., Elzerman, J. M., Delley, Y. L., Miguel-Sanchez, J. & Imamoğlu, A. Coherent two-electron spin qubits in an optically active pair of coupled InGaAs quantum dots. Phys. Rev. Lett. 109, 107401 (2012).
Reithmaier, G. et al. On-chip time resolved detection of quantum dot emission using integrated superconducting single photon detectors. Sci. Rep. 3, 1901 (2013).
Arcari, M. et al. Near-unity coupling efficiency of a quantum emitter to a photonic crystal waveguide. Phys. Rev. Lett. 113, 093603 (2014).
Acknowledgements
The Authors acknowledge many useful discussions with M. Kroner. This work is supported by NCCR Quantum Photonics (NCCR QP), the research instrument of the Swiss National Science Foundation (SNSF), and by the Swiss NSF under Grant No. 200020-159196.
Author information
Authors and Affiliations
Contributions
All authors contributed extensively to this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1523 kb)
Rights and permissions
About this article
Cite this article
Delteil, A., Sun, Z., Gao, Wb. et al. Generation of heralded entanglement between distant hole spins. Nature Phys 12, 218–223 (2016). https://doi.org/10.1038/nphys3605
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3605
This article is cited by
-
A diamond nanophotonic interface with an optically accessible deterministic electronuclear spin register
Nature Photonics (2024)
-
Applications of single photons to quantum communication and computing
Nature Reviews Physics (2023)
-
Quantum networks with neutral atom processing nodes
npj Quantum Information (2023)
-
Coherent memory for microwave photons based on long-lived mechanical excitations
npj Quantum Information (2023)
-
Ideal refocusing of an optically active spin qubit under strong hyperfine interactions
Nature Nanotechnology (2023)