Abstract
Photocurrent measurements provide a powerful means of studying the spatially resolved optoelectronic and electrical properties of a material or device1,2,3,4,5,6,7. Generally speaking there are two classes of mechanism for photocurrent generation: those involving separation of electrons and holes, and thermoelectric effects driven by electron temperature gradients. Here we introduce a new member in the latter class: the photo-Nernst effect. In graphene devices in a perpendicular magnetic field we observe photocurrent generated uniformly along the free edges, with opposite sign at opposite edges. The signal is antisymmetric in field, shows a peak versus gate voltage at the neutrality point flanked by wings of opposite sign at low fields, and exhibits quantum oscillations at higher fields. These features are all explained by the Nernst effect8,9,10 associated with laser-induced electron heating6,11,12,13,14. This ‘photo-Nernst’ current provides a simple and clear demonstration of the Shockley–Ramo nature of long-range photocurrent generation in a gapless material5.
Similar content being viewed by others
Main
In a semiconductor, electrons and holes generated by photons can live long enough to be spatially separated by an electric field and diffuse to the contacts. This is the basis of photovoltaic cell operation. In contrast, in a gapless material such as graphene the full electron distribution rapidly thermalizes, eliminating the distinction between electrons and holes. Nevertheless, photocurrent is readily produced when light is focused on inhomogeneous regions or junctions in graphene devices6,7,13,14,15,16,17,18,19,20. Detailed measurements of the dependence on gate voltage and time delay have shown that it is primarily of a thermoelectric nature6,11,13,17,19, and that the heating of the electrons is sometimes enhanced by slow energy transfer to the lattice due to the large optical phonon energy and high electron velocity14,21,22,23,24,25,26. However, the means by which a thermoelectric current near the laser spot results in photocurrent in the contacts, which may be located some distance away, has received much less attention.
Unlike in a semiconductor, in graphene one cannot talk about diffusion of majority carriers to the contacts. Rather, in such a gapless material the localized current density source jloc produces a global photocurrent Iph by setting up an electric field that drives ambient carriers outside the excitation region and into the contacts, as recently discussed by Song and Levitov5. These authors derived an expression giving Iph as an integral over jloc, analogous to the Shockley–Ramo theorem that gives the current generated between two conducting plates when a charge moves in the insulating space between them27,28. Our measurements on graphene devices in a magnetic field demonstrate the existence of the photo-Nernst effect which produces a photocurrent according to this theorem. In the presence of a perpendicular field B a transverse current proportional to B tends to circulate around the laser spot, that is, perpendicular to the electron temperature gradient in the graphene generated by the laser. When the laser is near a free edge, the integral of this chiral jloc points along the edge, producing a photocurrent which is independent of distance from the contacts. The agreement of the observed dependence on gate voltage and magnetic field with conventional thermoelectric measurements on graphene Hall bars8,9,10 firmly establishes the photo-Nernst origin of the response.
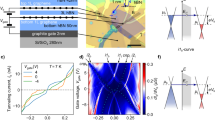
We studied two-terminal monolayer devices of graphene on SiO2 selected to have relatively low disorder (see Methods). Results from one device are shown throughout, but consistent results were obtained on several devices. An optical image of the device is shown in Fig. 1a. A gate voltage Vg is applied to the conducting Si substrate, and all measurements are made at a stage temperature of 40 K. Figure 1b shows the conductance at B = 0 as a function of gate voltage ΔVg measured relative to the conductance minimum (neutrality point), which in this device was at Vg0 = 1.3 V. The field-effect mobility is roughly 2 × 104 cm2 V−1 s−1. To measure photocurrent, a laser (wavelength 632 nm, spot size ∼1 μm) is focused on the surface and the short-circuit current Iph is detected, in the direction indicated. The laser power was kept at 40 μW, after determining that Iph is linear in power up to 60 μW (Supplementary Fig. 1). Scanning photocurrent microscopy (SPCM) was performed by measuring Iph as a function of the laser spot position.
a, Optical image of the device and indication of the experimental set-up. The graphene free edges are marked by dashed lines. b, Conductance at 40 K and B = 0 versus gate voltage ΔVg = Vg − Vg0 measured relative to the charge neutrality point, Vg0 = +1.3 V. c–e, SPCM images at B = 0 (c), +0.3 T (d) and −0.3 T (e), for the indicated values of ΔVg. The contact edges are indicated by thin white lines. Scale bar, 2 μm.
Figure 1c shows SPCM images taken at B = 0 at a series of four gate voltages. As usual in higher-mobility graphene devices, photocurrent is generated mostly near the contacts and is larger at gate voltages near the neutrality point. Figure 1d, e show corresponding images at B = +0.3 T and −0.3 T. Substantial additional photocurrent is now seen when the laser is near the graphene free edges yet far from the contacts. The polarity of this field-induced photocurrent is opposite at the upper and lower edges and reverses when the field is reversed. In Fig. 2a, b we plot the B-symmetric and antisymmetric parts of Iph, respectively, at ΔVg = +5 V. The symmetric part is very similar to the B = 0 photocurrent, whereas the antisymmetric part consists of two stripes, of opposite polarity, parallel to the edges and having almost uniform intensity along each edge.
a,b, B-symmetric and B-antisymmetric components, respectively, of the photocurrent data shown in Fig. 1 at ΔVg = +5 V, B = 0.3 T. Scale bar, 2 μm. The colour scale is the same as in Fig. 1. c, Cartoon indicating the electron temperature rise created near the laser spot in a simplified rectangular model of the device, showing the resulting Nernst current jN. d, Result of applying equation (1) to this model (with a multiplicative factor in the colour scale chosen to best match a). e, Comparison of model and measured photocurrent along the dotted green line in b. f,g, Calculated B-antisymmetric current density profiles within the model, illustrating how photocurrent is generated near the edge (laser at point f) but not in the centre (point g).
All of these observations can be understood by starting with the assumption that there is an increase in the electron temperature T(x, y) in and around the laser spot, which generates a thermoelectric current. Because the electron distribution thermalizes in ∼100 fs, T should be well defined on a scale of ∼100 nm. In similar zero-field measurements it has been shown to rise a few degrees above the lattice temperature6. At zero magnetic field and a given gate voltage, the thermoelectric current is parallel and proportional to ∇T, and by mirror symmetry this produces no net photocurrent when the spot is near an edge but far from the contacts. However, in a normal magnetic field  there exists a thermoelectric current density component jN that is odd in B and directed normal to ∇T, as indicated in Fig. 2c. When the spot is near an edge this current density tends to point along the edge. When the spot is near the opposite edge the current density points in the opposite direction. Because of its long-range Shockley–Ramo nature, the resulting photocurrent is independent of the location of the spot along the edge and reflects the directionality of jN. The gate-voltage dependence is produced by the dependence of the thermoelectric coefficients on carrier density.
there exists a thermoelectric current density component jN that is odd in B and directed normal to ∇T, as indicated in Fig. 2c. When the spot is near an edge this current density tends to point along the edge. When the spot is near the opposite edge the current density points in the opposite direction. Because of its long-range Shockley–Ramo nature, the resulting photocurrent is independent of the location of the spot along the edge and reflects the directionality of jN. The gate-voltage dependence is produced by the dependence of the thermoelectric coefficients on carrier density.
We can model the results quantitatively by applying Song and Levitov’s theorem5 to the extrinsic thermoelectric current jth = −α⃡∇T, with α⃡ the 2D thermoelectric tensor. Use of this local relationship is justified as the momentum relaxation length is less than29 ∼1 μm. The total current density j = jth + jd, which obeys the continuity equation ∇⋅j = 0, also includes a part jd (not parallel to ∇T if α⃡ is non-diagonal) driven by the electrochemical potential gradient that builds up. The resulting photocurrent is then given by Iph = ∬jth ⋅∇ψdxdy. Here the auxiliary scalar field ψ(x, y) is such that −(ρ⃡T)−1∇ψ is the current distribution created when a unit bias is applied between the contacts at jth = 0, and ρ⃡ is the 2D resistivity tensor.
For the particular case of a rectangular strip of isotropic 2D material, with contacts at x = 0 and L and free edges at y = 0 and W, far from the contacts one finds  , where r = (ρxy/ρxx) and the coefficient β < 1 depends on contact details. The photocurrent is then
, where r = (ρxy/ρxx) and the coefficient β < 1 depends on contact details. The photocurrent is then

The term involving (∂T/∂x), which is even in B, gives zero on integration if the temperature rise at the contacts is negligible (or if it is the same at both ends). The other term is odd in B and is proportional to the average temperature difference ΔTav between the two free edges:

From the definition of the Nernst coefficient N as the ratio of the transverse electric field to the longitudinal temperature gradient times the magnetic field at zero charge current, it immediately follows that −(αxy + rαxx) = NB/ρxx for isotropic material. Hence, for a rectangular device, when the laser spot is far from the contacts,

We conclude that the photocurrent is proportional to the Nernst coefficient divided by the longitudinal resistivity. This is likely to remain approximately true for less regularly shaped graphene.
It can be seen from equation (1) that this ‘photo-Nernst’ current will be odd in B, largest when the laser is near an edge (thus maximizing ΔTav), opposite in polarity at opposite edges, and independent of position along the edge when the laser is far from the contacts. All these facts are consistent with our observations. To be more quantitative, we performed a calculation of Iph for the rectangular strip model. We calculated ΔTav as a function of laser spot position by solving the heat equation given parameters reported in the literature for graphene on SiO2 of similar mobility (see Supplementary Information). With these parameters, heat flow to the substrate (by optical phonon coupling) dominates lateral heat flow in the graphene30, unlike in very high mobility devices31. In this limit the temperature rises only close to the region where power is absorbed, explaining why photocurrent is produced mostly at distances roughly within the size of the laser spot from the contacts or edges; and ΔTav is not very sensitive to the thermal conductivity of the graphene. A spatial pattern very similar to that in Fig. 2b was obtained with just two fitting parameters, the laser spot size and an overall multiplicative factor, as shown in Fig. 2d. A comparison of the calculated transverse profile with the measured photocurrent along the dotted green line in Fig. 2b is shown in Fig. 2e.
To provide more intuition for the long-range photocurrent generation process, we show in Fig. 2f, g calculated patterns of the B-antisymmetric component of the total current density j that can readily be computed in this simple geometry (see Supplementary Information). When the spot is near the top edge (f), the Nernst effect drives current predominantly to the right (taking N to be negative). Continuity, and the fact that jd cannot flow in a closed loop, causes the current flow lines to continue into the contacts. When the laser spot is in the centre of the strip (g), the net photocurrent is zero, although the Nernst effect produces a circulating current within the graphene. The largest photocurrent occurs slightly inside the edge because the temperature rise is slightly larger when more of the laser spot is on the graphene.
We now consider the dependence of the photo-Nernst current on Vg and B. The Nernst effect in graphene Hall bars has been measured before by conventional means8,9,10, and considered theoretically32. If the Mott relation33 applies then N can be written in terms of the components of ρ⃡:

Here kB is Boltzmann’s constant, e the magnitude of the electronic charge, and εF the Fermi energy. Putting this into equation (1) gives, for a fixed temperature,

The Mott relation assumes purely elastic, independent-electron transport and a slowly varying density of states. It should not apply when εF is within several kT of the Dirac point in perfect graphene. However, the behaviour of transport properties near the neutrality point in real devices is obscured by density inhomogeneities, and deviations from equation (2) may be hard to detect.
Figure 3 shows how the photocurrent depends on gate voltage at a moderate magnetic field, B = −0.3 T. Its magnitude and polarity change with Vg, whereas the maxima remain at the same spatial positions near the edges, as can be seen in Fig. 3a. The top axis here shows the 2D carrier density, defined by n = (C/e)(Vg −Vg0), taking (C/e) = (εrε0/edox) = 7.2 × 1010 cm−2 V−1 for oxide thickness dox = 300 nm and εr = 3.9. n is negative for holes, and loses meaning near the neutrality point owing to density inhomogeneities. Figure 3b shows the dependence on Vg at a fixed laser position (corresponding to the white dashed line in Fig. 3a). The photocurrent exhibits a peak at the neutrality point, changes sign for electron or hole density above ∼1011 cm−2, and decays slowly at higher densities. Both the peak at the neutrality point and the opposite-sign tails at higher density are consistent with previous Nernst measurements8,9,10 and are qualitatively explained by the energy derivative of ρxy in equation (2). If the width of the peak, δn ∼ 1011 cm−2, is set by density inhomogeneities, it should be similar to the width of the resistance peak at the neutrality point, shown in Fig. 3c. The two are indeed fairly similar. We note that the slight difference in the gate-voltage position of the peaks on the upper and lower edges apparent in Fig. 3a can be explained by a density variation across the sample.
a, Variation of photocurrent with transverse position y, along the dotted green line in Fig. 2b, as a function of gate voltage at B = −0.3 T. The top axis shows the corresponding 2D carrier density. b, Photocurrent versus gate voltage at a fixed position, corresponding to the dashed line in a. c, Two-terminal resistance for comparison.
At higher magnetic field quantum oscillations develop7 as a function of Vg, as illustrated in Fig. 4a. The variation of the peak photocurrent with Vg at a series of magnetic fields is shown in Fig. 4b. For the data at 3 T the filling factor ν = nh/eB is shown on the top axis. Again, the results resemble previous Nernst measurements8,9,10 and are qualitatively explained by equation (2), with the oscillations reflecting the energy derivative of the Shubnikov–de Haas oscillations in ρxx. The oscillations are thus large on a small background, in contrast with the much weaker oscillations in the resistance, which is shown in Fig. 4c. We note, however, that one needs to measure ρxx employing a multiterminal device to determine N accurately using equation (1).
a, Variation with carrier density of the photocurrent along a line across the graphene strip at 3 T. The top axis shows the corresponding Landau level filling factor. b, Maximum photocurrent versus carrier density at a series of magnetic fields. c, Two-terminal resistance measured under the same conditions as in b.
We finish by pointing out that scanning photo-Nernst microscopy could be used as a powerful new probe of materials and devices. For graphene the signal is large and easily detected at low fields (for example, 50 mT, Supplementary Fig. 2), and at room temperature (Supplementary Fig. 3). It can be measured on a simple two-terminal sample, where scanning can reveal spatial variations of properties. It can be separated from other photocurrent contributions by extracting the B-antisymmetric signal. Extended to lower temperatures and higher magnetic fields, the technique should yield new insights into the integer and fractional quantum Hall regimes. In those regimes, edge states and correlations may violate the conditions of locality or elastic single-particle transport. Finally, as the photo-Nernst signal shows much stronger quantum oscillations than the resistivity, it can be used to investigate the quasiparticle properties of materials with short scattering times, as has been done with conventional Nernst measurements on cuprates34 and bismuth35.
Methods
Monolayer graphene flakes were prepared by exfoliation onto substrates consisting of 300 nm-thick thermally oxidized SiO2 on highly p-doped silicon, which served as a back gate. Metal (Cr/Au) contacts were patterned by standard e-beam lithography and metallization in an e-beam evaporator. The two-terminal resistance was measured with an a.c. 100 nA current excitation at 20 Hz. For photocurrent measurements, the laser was mechanically chopped at 2 kHz and the current in phase with the chopper was detected.
References
Zhong, Z., Gabor, N. M., Sharping, J. E., Gaeta, A. L. & McEuen, P. L. Terahertz time-domain measurement of ballistic electron resonance in a single-walled carbon nanotube. Nature Nanotech. 3, 201–205 (2008).
McIver, J. W., Hsieh, D., Steinberg, H., Jarillo-Herrero, P. & Gedik, N. Control over topological insulator photocurrents with light polarization. Nature Nanotech. 7, 96–100 (2012).
Drexler, C. et al. Magnetic quantum ratchet effect in graphene. Nature Nanotech. 8, 104–107 (2013).
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014).
Song, J. C. W. & Levitov, L. S. Shockley–Ramo theorem and long-range photocurrent response in gapless materials. Phys. Rev. B 90, 075415 (2014).
Gabor, N. M. et al. Hot carrier–assisted intrinsic photoresponse in graphene. Science 334, 648–652 (2011).
Nazin, G., Zhang, Y., Zhang, L., Sutter, E. & Sutter, P. Visualization of charge transport through Landau levels in graphene. Nature Phys. 6, 870–874 (2010).
Zuev, Y. M., Chang, W. & Kim, P. Thermoelectric and Magnetothermoelectric transport measurements of graphene. Phys. Rev. Lett. 102, 096807 (2009).
Wei, P., Bao, W., Pu, Y., Lau, C. N. & Shi, J. Anomalous thermoelectric transport of Dirac particles in graphene. Phys. Rev. Lett. 102, 166808 (2009).
Checkelsky, J. G. & Ong, N. P. Thermopower and Nernst effect in graphene in a magnetic field. Phys. Rev. B 80, 081413 (2009).
Song, J. C. W., Rudner, M. S., Marcus, C. M. & Levitov, L. S. Hot carrier transport and photocurrent response in graphene. Nano Lett. 11, 4688–4692 (2011).
Ma, Q. et al. Competing channels for hot-electron cooling in graphene. Phys. Rev. Lett. 112, 247401 (2014).
Sun, D. et al. Ultrafast hot-carrier-dominated photocurrent in graphene. Nature Nanotech. 7, 114–118 (2012).
Graham, M. W., Shi, S.-F., Ralph, D. C., Park, J. & McEuen, P. L. Photocurrent measurements of supercollision cooling in graphene. Nature Phys. 9, 103–108 (2013).
LeeEduardo, J. H., Balasubramanian, K., Weitz, R. T., Burghard, M. & Kern, K. Contact and edge effects in graphene devices. Nature Nanotech. 3, 486–490 (2008).
Park, J., Ahn, Y. H. & Ruiz-Vargas, C. Imaging of photocurrent generation and collection in single-layer graphene. Nano Lett. 9, 1742–1746 (2009).
Xu, X., Gabor, N. M., Alden, J. S., van der Zande, A. M. & McEuen, P. L. Photo-thermoelectric effect at a graphene interface junction. Nano Lett. 10, 562–566 (2009).
Liu, C.-H., Chang, Y.-C., Norris, T. B. & Zhong, Z. Graphene photodetectors with ultra-broadband and high responsivity at room temperature. Nature Nanotech. 9, 273–278 (2014).
Lemme, M. C. et al. Gate-activated photoresponse in a graphene p–n junction. Nano Lett. 11, 4134–4137 (2011).
Urich, A., Unterrainer, K. & Mueller, T. Intrinsic response time of graphene photodetectors. Nano Lett. 11, 2804–2808 (2011).
Song, J. C. W., Reizer, M. Y. & Levitov, L. S. Disorder-assisted electron-phonon scattering and cooling pathways in graphene. Phys. Rev. Lett. 109, 106602 (2012).
Betz, A. C. et al. Supercollision cooling in undoped graphene. Nature Phys. 9, 109–112 (2013).
Johannsen, J. C. et al. Direct view of hot carrier dynamics in graphene. Phys. Rev. Lett. 111, 027403 (2013).
Tielrooij, K. J. et al. Photoexcitation cascade and multiple hot-carrier generation in graphene. Nature Phys. 9, 248–252 (2013).
Yan, J. et al. Dual-gated bilayer graphene hot-electron bolometer. Nature Nanotech. 7, 472–478 (2012).
Lui, C. H., Mak, K. F., Shan, J. & Heinz, T. F. Ultrafast photoluminescence from graphene. Phys. Rev. Lett. 105, 127404 (2010).
Shockley, W. Currents to conductors induced by a moving point charge. J. Appl. Phys. 9, 635–636 (1938).
Ramo, S. Currents induced by electron motion. Proc. IRE 27, 584–585 (1939).
Miao, F. et al. Phase-coherent transport in graphene quantum billiards. Science 317, 1530–1533 (2007).
Freitag, M. et al. Energy dissipation in graphene field-effect transistors. Nano Lett. 9, 1883–1888 (2009).
Balandin, A. A. et al. Superior thermal conductivity of single-layer graphene. Nano Lett. 8, 902–907 (2008).
Luk’yanchuk, I. A., Varlamov, A. A. & Kavokin, A. V. Giant Nernst–Ettingshausen oscillations in semiclassically strong magnetic fields. Phys. Rev. Lett. 107, 016601 (2011).
Jonson, M. & Girvin, S. M. Thermoelectric effect in a weakly disordered inversion layer subject to a quantizing magnetic field. Phys. Rev. B 29, 1939–1946 (1984).
Wang, Y., Li, L. & Ong, N. P. Nernst effect in high-TC superconductors. Phys. Rev. B 73, 024510 (2006).
Behnia, K., Méasson, M.-A. & Kopelevich, Y. Oscillating Nernst–Ettingshausen effect in bismuth across the quantum limit. Phys. Rev. Lett. 98, 166602 (2007).
Acknowledgements
We thank B. Spivak, A. Andreev, D. Xiao and C. Laumann for discussions. This work was supported by the National Science Foundation (NSF, DMR-1150719). The experimental set-up was partially supported by DoE BES (DE-SC0008145). Z.F. and D.H.C. are supported by DoE BES (DE-SC0002197). This material is based in part upon work supported by the State of Washington through the University of Washington Clean Energy Institute. Device fabrication was performed at the University of Washington Microfabrication Facility and the NSF-funded Nanotech User Facility.
Author information
Authors and Affiliations
Contributions
X.X. conceived the experiment; G.A. built the experimental set-up; H.C. performed the experiments, assisted by G.A.; H.C., Z.F. and J.R. fabricated the devices; H.C., X.X., D.H.C. and Z.F. analysed the results; Z.F. and D.H.C. did the modelling; and H.C., D.H.C. and X.X. wrote the paper with comments from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 826 kb)
Rights and permissions
About this article
Cite this article
Cao, H., Aivazian, G., Fei, Z. et al. Photo-Nernst current in graphene. Nature Phys 12, 236–239 (2016). https://doi.org/10.1038/nphys3549
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3549
This article is cited by
-
Visualization of bulk and edge photocurrent flow in anisotropic Weyl semimetals
Nature Physics (2023)
-
Photocurrent as a multiphysics diagnostic of quantum materials
Nature Reviews Physics (2023)
-
Infrared nano-imaging of Dirac magnetoexcitons in graphene
Nature Nanotechnology (2023)
-
Ultrafast photothermoelectric effect in Dirac semimetallic Cd3As2 revealed by terahertz emission
Nature Communications (2022)
-
Hyperbolic enhancement of photocurrent patterns in minimally twisted bilayer graphene
Nature Communications (2021)