Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Hierarchy of Hofstadter states and replica quantum Hall ferromagnetism in graphene superlattices

Nature Physics volume 10, pages 525–529 (2014)Cite this article

Subjects

An Erratum to this article was published on 30 September 2014

Abstract

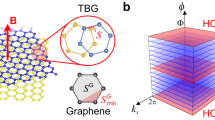
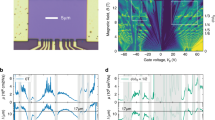
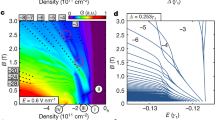
Self-similarity and fractals have fascinated researchers across various disciplines. In graphene placed on boron nitride and subjected to a magnetic field, self-similarity appears in the form of numerous replicas of the original Dirac spectrum, and their quantization gives rise to a fractal pattern of Landau levels, referred to as the Hofstadter butterfly. Here we employ capacitance spectroscopy to probe directly the density of states (DoS) and energy gaps in this spectrum. Without a magnetic field, replica spectra are seen as pronounced DoS minima surrounded by van Hove singularities. The Hofstadter butterfly shows up as recurring Landau fan diagrams in high fields. Electron–electron interactions add another twist to the self-similar behaviour. We observe suppression of quantum Hall ferromagnetism, a reverse Stoner transition at commensurable fluxes and additional ferromagnetism within replica spectra. The strength and variety of the interaction effects indicate a large playground to study many-body physics in fractal Dirac systems.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Capacitance spectroscopy of graphene superlattices.
Figure 2: Magnetocapacitance oscillations and quantized density of states.
Figure 3: Hofstadter butterfly in graphene superlattices.
Figure 4: Interactions in Hofstadter minibands.

References

  1. Xue, J. M. et al. Scanning tunnelling microscopy and spectroscopy of ultra-flat graphene on hexagonal boron nitride. Nature Mater. 10, 282–285 (2011).

    Article  ADS  Google Scholar 

  2. Decker, R. et al. Local electronic properties of graphene on a BN substrate via scanning tunneling microscopy. Nano Lett. 11, 2291–2295 (2011).

    Article  ADS  Google Scholar 

  3. Yankowitz, M. et al. Emergence of superlattice Dirac points in graphene on hexagonal boron nitride. Nature Phys. 8, 382–386 (2012).

    Article  ADS  Google Scholar 

  4. Ponomarenko, L. A. et al. Cloning of Dirac fermions in graphene superlattices. Nature 497, 594–597 (2013).

    Article  ADS  Google Scholar 

  5. Dean, C. R. et al. Hofstadter’s butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 497, 598–602 (2013).

    Article  ADS  Google Scholar 

  6. Hunt, B. et al. Massive Dirac fermions and Hofstadter butterfly in a van der Waals heterostructure. Science 340, 1427–1430 (2013).

    Article  ADS  Google Scholar 

  7. Park, C. H., Yang, L., Son, Y. W., Cohen, M. L. & Louie, S. G. New generation of massless Dirac fermions in graphene under external periodic potentials. Phys. Rev. Lett. 101, 126804 (2008).

    Article  ADS  Google Scholar 

  8. Barbier, M., Vasilopoulos, P. & Peeters, F. M. Extra Dirac points in the energy spectrum for superlattices on single-layer graphene. Phys. Rev. B 81, 075438 (2010).

    Article  ADS  Google Scholar 

  9. Wu, S., Killi, M. & Paramekanti, A. Graphene under spatially varying external potentials: Landau levels, magnetotransport, and topological modes. Phys. Rev. B 85, 195404 (2012).

    Article  ADS  Google Scholar 

  10. Ortix, C., Yang, L. & van den Brink, J. Graphene on incommensurate substrates: Trigonal warping and emerging Dirac cone replicas with halved group velocity. Phys. Rev. B 86, 081405 (2012).

    Article  ADS  Google Scholar 

  11. Wallbank, J. R., Patel, A. A., Mucha-Kruczynski, M., Geim, A. K. & Fal’ko, V. I. Generic miniband structure of graphene on a hexagonal substrate. Phys. Rev. B 87, 245408 (2013).

    Article  ADS  Google Scholar 

  12. Chen, X. et al. Dirac edges of fractal magnetic minibands in graphene with hexagonal moiré superlattices. Phys. Rev. B 89, 075401 (2014).

    Article  ADS  Google Scholar 

  13. Brown, E. Bloch electrons in a uniform magnetic field. Phys. Rev. 133, A1038–A1044 (1964).

    Article  ADS  MathSciNet  Google Scholar 

  14. Zak, J. Magnetic translation group. Phys. Rev. 134, A1602–A1611 (1964).

    Article  ADS  Google Scholar 

  15. Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).

    Article  ADS  Google Scholar 

  16. Pfannkuche, D. & Gerhardts, R. R. Theory of magnetotransport in two-dimensional electron systems subjected to weak two-dimensional superlattice potentials. Phys. Rev. B 46, 12606–12626 (1992).

    Article  ADS  Google Scholar 

  17. Albrecht, C. et al. Evidence of Hofstadter’s fractal energy spectrum in the quantized Hall conductance. Phys. Rev. Lett. 86, 147–150 (2001).

    Article  ADS  Google Scholar 

  18. Geisler, M. C. et al. Detection of a Landau band-coupling-induced rearrangement of the Hofstadter butterfly. Phys. Rev. Lett. 92, 256801 (2004).

    Article  ADS  Google Scholar 

  19. Bistritzer, R. & MacDonald, A. H. Moire butterflies. Phys. Rev. B 84, 035440 (2011).

    Article  ADS  Google Scholar 

  20. Yang, K., Das Sarma, S. & MacDonald, A. H. Collective modes and skyrmion excitations in graphene SU(4) quantum Hall ferromagnets. Phys. Rev. B 74, 075423 (2006).

    Article  ADS  Google Scholar 

  21. Goerbig, M. O. & Regnault, N. Analysis of a SU(4) generalization of Halperin’s wave function as an approach towards a SU(4) fractional quantum Hall effect in graphene sheets. Phys. Rev. B 75, 241405 (2007).

    Article  ADS  Google Scholar 

  22. Jiang, Z., Zhang, Y., Stormer, H. L. & Kim., P. Quantum Hall states near the charge-neutral Dirac point in graphene. Phys. Rev. Lett. 99, 106802 (2007).

    Article  ADS  Google Scholar 

  23. Young, A. F. et al. Spin and valley quantum Hall ferromagnetism in graphene. Nature Phys. 8, 550–556 (2012).

    Article  ADS  Google Scholar 

  24. Yu, G. L. et al. Interaction phenomena in graphene seen through quantum capacitance. Proc. Natl Acad. Sci. USA 110, 3282–3286 (2013).

    Article  ADS  Google Scholar 

  25. Kretinin, A. et al. Accurate determination of electron-hole asymmetry and next-nearest neighbor hopping in graphene. Phys. Rev. B 88, 165427 (2013).

    Article  ADS  Google Scholar 

  26. Woods, C. R. et al. Commensurate–incommensurate transition for graphene on hexagonal boron nitride. Nature Phys. 10, 451–456 (2014).

    Article  ADS  Google Scholar 

  27. Fang, T., Konar, A., Xing, H. & Jena, D. Carrier statistics and quantum capacitance of graphene sheets and nanoribbons. Appl. Phys. Lett. 91, 092109 (2007).

    Article  ADS  Google Scholar 

  28. Wannier, G. H. A result not dependent on rationality for Bloch electrons in a magnetic field. Phys. Status Solidi b 88, 757–765 (1978).

    Article  ADS  Google Scholar 

  29. Sondhi, S. L., Karlhede, A., Kivelson, S. A. & Rezayi, E. H. Skyrmions and the crossover from the integer to fractional quantum Hall effect at small Zeeman energies. Phys. Rev. B 47, 16419–16426 (1993).

    Article  ADS  Google Scholar 

  30. Fertig, H. A., Brey, L., Côté, R. & MacDonald, A. H. Charged spin-texture excitations and the Hartree–Fock approximation in the quantum Hall effect. Phys. Rev. B 50, 11018–11021 (1994).

    Article  ADS  Google Scholar 

  31. Barrett, S. E., Dabbagh, G., Pfeiffer, L. N., West, K. W. & Tycko, R. Optically pumped NMR evidence for finite-size skyrmions in GaAs quantum wells near Landau level filling ν = 1. Phys. Rev. Lett. 74, 5112–5115 (1995).

    Article  ADS  Google Scholar 

  32. Apalkov, V. M. & Chakraborty, T. Gap structure of the Hofstadter system of interacting Dirac fermions in graphene. Phys. Rev. Lett. 112, 176401 (2014).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the European Research Council, the Royal Society, Graphene Flagship, Science and Innovation Award from the EPSRC (UK) and EuroMagNET II (EU Contract 228043).

Author information

Authors and Affiliations

  1. School of Physics & Astronomy, University of Manchester, Manchester M13 9PL, UK

    G. L. Yu, L. A. Ponomarenko, D. C. Elias, I. V. Grigorieva, K. S. Novoselov, A. K. Geim & A. Mishchenko

  2. Centre for Mesoscience & Nanotechnology, University of Manchester, Manchester M13 9PL, UK

    R. V. Gorbachev, J. S. Tu, A. V. Kretinin, Y. Cao, R. Jalil, F. Withers & A. K. Geim

  3. Physics Department, Lancaster University, LA1 4YB, UK

    L. A. Ponomarenko, X. Chen & V. I. Fal’ko

  4. Laboratoire National des Champs Magnétiques Intenses, CNRS-UJF-UPS-INSA, F-38042 Grenoble, France

    B. A. Piot & M. Potemski

  5. Departamento de Física, Universidade Federal de Minas Gerais, 30123-970, Belo Horizonte, Brazil

    D. C. Elias

  6. National Institute for Materials Science, 1-1 Namiki, Tsukuba, 305-0044, Japan

    K. Watanabe & T. Taniguchi

Authors
  1. G. L. Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. V. Gorbachev
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. S. Tu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. V. Kretinin
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Y. Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. R. Jalil
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. F. Withers
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. L. A. Ponomarenko
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. B. A. Piot
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. M. Potemski
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. D. C. Elias
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. X. Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. K. Watanabe
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. T. Taniguchi
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. I. V. Grigorieva
    View author publications

    You can also search for this author in PubMed Google Scholar

  16. K. S. Novoselov
    View author publications

    You can also search for this author in PubMed Google Scholar

  17. V. I. Fal’ko
    View author publications

    You can also search for this author in PubMed Google Scholar

  18. A. K. Geim
    View author publications

    You can also search for this author in PubMed Google Scholar

  19. A. Mishchenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

J.S.T., A.V.K., Y.C., R.J. and F.W. designed and fabricated the devices. A.M. and G.L.Y. carried out the measurements. B.A.P. and M.P. helped with high-field experiments. X.C. and V.I.F. provided theoretical support. K.W. and T.T. provided hBN crystals. R.V.G. devised the fabrication technology for graphene capacitors. A.M. developed the on-chip capacitance bridge. A.M., V.I.F. and A.K.G. analysed the results. A.K.G. together with V.I.F. wrote the manuscript. K.S.N., I.V.G., L.A.P. and D.C.E. helped with experiments and/or writing the paper. Section 4 of the Supplementary Information was written by V.I.F. All authors contributed to discussions.

Corresponding authors

Correspondence to V. I. Fal’ko, A. K. Geim or A. Mishchenko.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 1279 kb)

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Yu, G., Gorbachev, R., Tu, J. et al. Hierarchy of Hofstadter states and replica quantum Hall ferromagnetism in graphene superlattices. Nature Phys 10, 525–529 (2014). https://doi.org/10.1038/nphys2979

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphys2979

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing