Abstract
The uncertainty principle, originally formulated by Heisenberg1, clearly illustrates the difference between classical and quantum mechanics. The principle bounds the uncertainties about the outcomes of two incompatible measurements, such as position and momentum, on a particle. It implies that one cannot predict the outcomes for both possible choices of measurement to arbitrary precision, even if information about the preparation of the particle is available in a classical memory. However, if the particle is prepared entangled with a quantum memory, a device that might be available in the not-too-distant future2, it is possible to predict the outcomes for both measurement choices precisely. Here, we extend the uncertainty principle to incorporate this case, providing a lower bound on the uncertainties, which depends on the amount of entanglement between the particle and the quantum memory. We detail the application of our result to witnessing entanglement and to quantum key distribution.
Similar content being viewed by others
Main
Uncertainty relations constrain the potential knowledge one can have about the physical properties of a system. Although classical theory does not limit the knowledge we can simultaneously have about arbitrary properties of a particle, such a limit does exist in quantum theory. Even with a complete description of its state, it is impossible to predict the outcomes of all possible measurements on the particle. This lack of knowledge, or uncertainty, was quantified by Heisenberg1 using the standard deviation (which we denote by ΔR for an observable R). If the measurement on a given particle is chosen from a set of two possible observables, R and S, the resulting bound on the uncertainty can be expressed in terms of the commutator3:

In an information-theoretic context, it is more natural to quantify uncertainty in terms of entropy rather than the standard deviation. Entropic uncertainty relations for position and momentum were derived in ref. 4 and later a relation was developed that holds for any pair of observables5. An improvement of this relation was subsequently conjectured6 and then proved7. The improved relation is

where H(R) denotes the Shannon entropy of the probability distribution of the outcomes when R is measured. The term 1/c quantifies the complementarity of the observables. For non-degenerate observables, c:=maxj,k|〈ψj|φk〉|2, where |ψj〉 and |φk〉 are the eigenvectors of R and S, respectively.
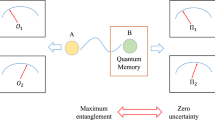
One way to think about uncertainty relations is through the following game (the uncertainty game) between two players, Alice and Bob. Before the game commences, Alice and Bob agree on two measurements, R and S. The game proceeds as follows. Bob prepares a particle in a quantum state of his choosing and sends it to Alice. Alice then carries out one of the two measurements and announces her choice to Bob. Bob’s task is to minimize his uncertainty about Alice’s measurement outcome. This is illustrated in Fig. 1.
(1) Bob sends a particle to Alice, which may, in general, be entangled with his quantum memory. (2) Alice measures either R or S and notes her outcome. (3) Alice announces her measurement choice to Bob. Our uncertainty relation provides a lower bound on Bob’s resulting uncertainty about Alice’s outcome.
Equation (1) bounds Bob’s uncertainty in the case that he has no quantum memory—all information Bob holds about the particle is classical, for example, a description of its density matrix. However, with access to a quantum memory, Bob can beat this bound. To do so, he should maximally entangle his quantum memory with the particle he sends to Alice. Then, for any measurement she chooses, there is a measurement on Bob’s memory that gives the same outcome as Alice obtains. Hence, the uncertainties about both observables, R and S, vanish, which shows that if one tries to generalize equation (1) by replacing the measure of uncertainty about R and S used there (the Shannon entropy) by the entropy conditioned on the information in Bob’s quantum memory, the resulting relation no longer holds.
We proceed by stating our uncertainty relation, which applies in the presence of a quantum memory. It provides a bound on the uncertainties of the measurement outcomes that depends on the amount of entanglement between the measured particle, A, and the quantum memory, B. Mathematically, it is the relation

The uncertainty about the outcome of measurement R given information stored in a quantum memory, B, is denoted by the conditional von Neumann entropy, H(R|B). The extra term H(A|B) appearing on the right-hand side quantifies the amount of entanglement between the particle and the memory. We sketch the proof of this relation in the Methods section and defer the full proof to the Supplementary Information.
We continue by discussing some instructive examples. First, if the particle, A, and memory, B, are maximally entangled, then H(A|B)=−log2d, where d is the dimension of the particle sent to Alice. As log21/c cannot exceed log2d, the bound in equation (2) reduces to H(R|B)+H(S|B)≥0, which is trivial, because the conditional entropy of a system after measurement given the quantum memory cannot be negative. As discussed above, Bob can guess both R and S perfectly with such a strategy. Second, if A and B are not entangled (that is, their state is a convex combination of product states) then H(A|B)≥0. As H(R|B)≤H(R) and H(S|B)≤H(S) for all states, we recover Maassen and Uffink’s bound, equation (1). Third, in the absence of the quantum memory, B, we can reduce the bound equation (2) to H(R)+H(S)≥log21/c+H(A). If the state of the particle, A, is pure, then H(A)=0 and we again recover the bound of Maassen and Uffink, equation (1). However, if the particle, A, is in a mixed state then H(A)>0 and the resulting bound is stronger than equation (1) even when there is no quantum memory. Fourth, in terms of new applications, the most interesting case is when A and B are entangled, but not maximally so. As a negative conditional entropy H(A|B) is a signature of entanglement8, the uncertainty relation takes into account the entanglement between the particle and the memory. It is therefore qualitatively different from existing classical bounds.
Aside from its fundamental significance, our result has an impact on the development of future quantum technologies. In the following, we will explain how it can be applied to the task of witnessing entanglement and to construct security proofs in quantum cryptography.
For the application to witnessing entanglement, consider a source that emits a two-particle state ρA B. Analogously to the uncertainty game, we measure A with one of two observables, R or S. Furthermore, a second measurement (of R′ or S′) should be applied to B trying to reproduce the outcome of the first. The probability with which the measurements on A and B disagree can be directly used to upper bound the entropies H(R|B) and H(S|B). For example, using Fano’s inequality, we obtain H(R|B)≤h(pR)+pRlog2(d−1), where pR is the probability that the outcomes of R and R′ are not equal and h is the binary entropy function. If this bound and the analogous bound for H(S|B) are sufficiently small, then our result, equation (2), implies that H(A|B) must be negative, and hence that ρA B is entangled.
Note that this method of witnessing entanglement does not involve an (usually experimentally challenging) estimation of the D2 matrix elements of ρA B, where D is the dimension of A B—it is sufficient to estimate the two probabilities pR and pS, which can be obtained by separate measurements on each of the two particles. Our method also differs significantly from the standard approach that is based on collecting measurement statistics to infer the expectation values of fixed witness observables on the joint system of both particles9,10,11,12. We remark that when using our procedure, the best choice of Alice’s observables are ones with high complementarity, 1/c.
As a second application, we consider quantum key distribution. More than twenty years ago, new cryptographic protocols based on quantum theory were proposed13,14, most famously the BB84 quantum key distribution protocol14. Their intuition for security lay in the uncertainty principle. In spite of providing the initial intuition, most security proofs so far have not involved uncertainty relations (see, for example, refs 1516, 16, 17, 18, 19, 20), although ref. 21 provides a notable exception. The obstacle for the use of the uncertainty principle is quickly identified: a full proof of security must take into account a technologically unbounded eavesdropper, that is, one who potentially has access to a quantum memory. In the following, we explain how to use our main result, equation (2), to overcome this obstacle and derive a simple bound on the key rate.
Building on the idea proposed in ref. 22, the security of quantum key distribution protocols is usually analysed by assuming that the eavesdropper creates a quantum state, ρA B E, and distributes the A and B parts to the two users, Alice and Bob. In practice, Alice and Bob do not provide the eavesdropper with this luxury, but a security proof that applies even in this case will certainly imply security when Alice and Bob distribute the states themselves. To generate their key, Alice and Bob measure the states they receive using measurements chosen at random, with Alice’s possible measurements denoted by R and S and Bob’s by R′ and S′. To ensure that the same key is generated, they communicate their measurement choices to one another. In the worst case, this communication is overheard in its entirety by the eavesdropper who is trying to obtain the key. Even so, Alice and Bob can generate a secure key if their measurement outcomes are sufficiently well correlated.
To show this, we use a result of ref. 8, namely that the amount of key Alice and Bob are able to extract per state, K, is lower bounded by H(R|E)−H(R|B). In addition, we reformulate our main result, equation (2), as H(R|E)+H(S|B)≥log21/c, a form previously conjectured by Boileau and Renes23 (see Supplementary Information). Together these imply K≥log21/c−H(R|B)−H(S|B). Furthermore, using the fact that measurements cannot decrease entropy, we have

This corresponds to a generalization of the result of ref. 17, which is recovered in the case of conjugate observables applied to qubits and assuming symmetry, that is, H(R|R′)=H(S|S′). The argument given here applies only to collective attacks but can be extended to arbitrary attacks using the post-selection technique24.
This security argument has the advantage that Alice and Bob need to upper bound only the entropies H(R|R′) and H(S|S′). Similarly to the case of entanglement witnessing, these entropies can be directly bounded by observable quantities, such as the frequency with which Alice and Bob’s outcomes agree. No further information about the state is required. This improves the performance of practical quantum key distribution schemes, where the amount of statistics needed to estimate states is critical for security25.
The range of application of our result, equation (2), is not restricted to these two examples, but extends to other cryptographic scenarios26, a quantum phenomenon known as locking of information27 (in the way presented in ref. 28) and to decoupling theorems that are frequently used in coding arguments23.
Finally, we note that uncertainty may be quantified in terms of alternative entropy measures. In fact, our proof involves smooth entropies, which can be seen as generalizations of the von Neumann entropy20 (see the Methods section and Supplementary Information). These generalizations have direct operational interpretations29 and are related to physical quantities, such as thermodynamic entropy. We therefore expect a formulation of the uncertainty relation in terms of these generalized entropies to have further use both in quantum information theory and beyond.
Methods
Here we outline the proof of the main result, equation (2). The quantities appearing there are evaluated for a state ρA B, where we use H(R|B) to denote the conditional von Neumann entropy of the state

and likewise for H(S|B).
The proof is fully based on the smooth entropy calculus introduced in ref. 20 and proceeds in three steps (see Supplementary Information for further details, including precise definitions of the quantities used in this section). In the first step, which we explain in more detail below, an uncertainty relation is proved that is similar to equation (2) but with the von Neumann entropy being replaced by the min- and max-entropies, denoted Hmin and Hmax, respectively (we also use  , which plays a role similar to Hmax):
, which plays a role similar to Hmax):

The quantities  and Hmin involve only the extremal eigenvalues of an operator, which makes them easier to deal with than the von Neumann entropy, which depends on all eigenvalues. In the second, technically most involved step of the proof, we extend the relation to the smooth min- and max-entropies, which are more general and allow us to recover the relation for the von Neumann entropy as a special case.
and Hmin involve only the extremal eigenvalues of an operator, which makes them easier to deal with than the von Neumann entropy, which depends on all eigenvalues. In the second, technically most involved step of the proof, we extend the relation to the smooth min- and max-entropies, which are more general and allow us to recover the relation for the von Neumann entropy as a special case.
The ɛ-smooth min- and max-entropies are formed by taking the original entropies and extremizing them over a set of states ɛ-close to the original (where closeness is quantified in terms of the maximum purified distance from the original). In this step we also convert  to a smooth max-entropy and obtain the relation
to a smooth max-entropy and obtain the relation

which holds for any ɛ>0.
To complete the proof, we evaluate the inequality on the n-fold tensor product of the state in question, that is, on  . We then use the asymptotic equipartition theorem20,30, which tells us that the smooth min- and max-entropies tend to the von Neumann entropy in the appropriate limit, that is,
. We then use the asymptotic equipartition theorem20,30, which tells us that the smooth min- and max-entropies tend to the von Neumann entropy in the appropriate limit, that is,

Hence, on both sides of equation (4), we divide by n and take the limit as in the previous equation to obtain

from which our main result, equation (2), follows by subtracting H(B) from both sides.
We now sketch the first step of the proof. This develops an idea from refs 23, 28 where uncertainty relations that apply only to the case of complementary observables (that is, those related by a Fourier transform) are derived. These relations were originally expressed in terms of von Neumann entropies rather than min- and max-entropies.
We use two chain rules and strong subadditivity of the min-entropy, to show that, for a system composed of subsystems A′B′A B and for a state Ω,

We now apply this relation to the state ΩA′B′A B defined as follows:

where {|a〉}a and {|b〉}b are orthonormal bases on d-dimensional Hilbert spaces  and
and  , respectively, and DR and DS are the operators that dephase in the respective eigenbases of R and S. Hence, tracing out A′ (B′) reduces the state to one where the system, A, is measured in the eigenbasis of R (S) and the outcome forgotten. We then use properties of the entropies to relate the quantities
, respectively, and DR and DS are the operators that dephase in the respective eigenbases of R and S. Hence, tracing out A′ (B′) reduces the state to one where the system, A, is measured in the eigenbasis of R (S) and the outcome forgotten. We then use properties of the entropies to relate the quantities  and Hmin(B′A|B)Ω from equation (5) to
and Hmin(B′A|B)Ω from equation (5) to  and Hmin(R|B), respectively, in spite of the fact that R and S neither commute nor anticommute—a property that makes it difficult to complete the proof directly with the von Neumann entropy. Furthermore, Hmin(A′B′A B)Ω is easily related to Hmin(A B). Finally, tracing out both A′ and B′ reduces the state to one where the system, A, is measured first with one observable and then with the other and the outcomes forgotten. Hence, the term Hmin(A|B)Ω can be related to the overlap of the eigenvectors of the two observables, c.
and Hmin(R|B), respectively, in spite of the fact that R and S neither commute nor anticommute—a property that makes it difficult to complete the proof directly with the von Neumann entropy. Furthermore, Hmin(A′B′A B)Ω is easily related to Hmin(A B). Finally, tracing out both A′ and B′ reduces the state to one where the system, A, is measured first with one observable and then with the other and the outcomes forgotten. Hence, the term Hmin(A|B)Ω can be related to the overlap of the eigenvectors of the two observables, c.
Bringing everything together, we obtain the desired uncertainty relation, equation (3).
References
Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 43, 172–198 (1927).
Julsgaard, B., Sherson, J., Cirac, J. I., Fiurášek, J. & Polzik, E. S. Experimental demonstration of quantum memory for light. Nature 432, 482–486 (2004).
Robertson, H. P. The uncertainty principle. Phys. Rev. 34, 163–164 (1929).
Białynicki-Birula, I. & Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 44, 129–132 (1975).
Deutsch, D. Uncertainty in quantum measurements. Phys. Rev. Lett. 50, 631–633 (1983).
Kraus, K. Complementary observables and uncertainty relations. Phys. Rev. D 35, 3070–3075 (1987).
Maassen, H. & Uffink, J. B. Generalized entropic uncertainty relations. Phys. Rev. Lett. 60, 1103–1106 (1988).
Devetak, I. & Winter, A. Distillation of secret key and entanglement from quantum states. Proc. R. Soc. A 461, 207–235 (2005).
Horodecki, M., Horodecki, P. & Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 223, 1–8 (1996).
Terhal, B. M. Bell inequalities and the separability criterion. Phys. Lett. A 271, 319–326 (2000).
Lewenstein, M., Kraus, B., Cirac, J. I. & Horodecki, P. Optimization of entanglement witnesses. Phys. Rev. A 62, 1–16 (2000).
Gühne, O. & Tóth, G. Entanglement detection. Phys. Rep. 747, 1–75 (2009).
Wiesner, S. Conjugate coding. Sigact News 15, 78–88 (1983).
Bennett, C. H. & Brassard, G. in Proc. IEEE Int. Conf. on Computers, Systems and Signal Processing, Bangalore, India 175–179 (IEEE, 1984).
Deutsch, D. et al. Quantum privacy amplification and the security of quantum cryptography over noisy channels. Phys. Rev. Lett. 77, 2818–2821 (1996).
Lo, H-K. & Chau, H. F. Unconditional security of quantum key distribution over arbitrarily long distances. Science 283, 2050–2056 (1999).
Shor, P. W. & Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441–444 (2000).
Christandl, M., Renner, R. & Ekert, A. A generic security proof for quantum key distribution. Preprint at http://arxiv.org/abs/quant-ph/0402131 (2004).
Renner, R. & König, R. Universally composable privacy amplification against quantum adversaries. Theory of Cryptography Conference, TCC 2005 407–425 (Lecture Notes in Computer Science, Vol. 3378, Springer, 2005).
Renner, R. Security of quantum key distribution. Int. J. Quantum Inform. 6, 1–127 (2008).
Koashi, M. Unconditional security of quantum key distribution and the uncertainty principle. J. Phys. Conf. Ser. 36, 98–102 (2006).
Ekert, A. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Renes, J. M. & Boileau, J-C. Conjectured strong complementary information tradeoff. Phys. Rev. Lett. 103, 020402 (2009).
Christandl, M., König, R. & Renner, R. Postselection technique for quantum channels with applications to quantum cryptography. Phys. Rev. Lett. 102, 020504 (2009).
Renner, R. & Scarani, V. Quantum cryptography with finite resources: Unconditional security bound for discrete-variable protocols with one-way postprocessing. Phys. Rev. Lett. 100, 200501 (2008).
Chandran, N., Fehr, S., Gelles, R., Goyal, V. & Ostrovsky, R. Position-based quantum cryptography. Preprint at http://arxiv.org/abs/1005.1750 (2010).
DiVincenzo, D. P., Horodecki, M., Leung, D. W., Smolin, J. A. & Terhal, B. M. Locking classical correlations in quantum states. Phys. Rev. Lett. 92, 067902 (2004).
Christandl, M. & Winter, A. Uncertainty, monogamy and locking of quantum correlations. IEEE Trans. Inf. Theory 51, 3159–3165 (2005).
König, R., Renner, R. & Schaffner, C. The operational meaning of min- and max-entropy. IEEE Trans. Inf. Theory 55, 4337–4347 (2009).
Tomamichel, M., Colbeck, R. & Renner, R. A fully quantum asymptotic equipartition property. IEEE Trans. Inf. Theory 55, 5840–5847 (2009).
Acknowledgements
We thank R. König, J. Oppenheim and M. Tomamichel for discussions and L. del Rio for the illustration (Fig. 1). M.B. and M.C. acknowledge support from the German Science Foundation (DFG) and the Swiss National Science Foundation. J.M.R. acknowledges the support of the Center for Advanced Security Research Darmstadt (CASED). R.C. and R.R. acknowledge support from the Swiss National Science Foundation.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 408 kb)
Rights and permissions
About this article
Cite this article
Berta, M., Christandl, M., Colbeck, R. et al. The uncertainty principle in the presence of quantum memory. Nature Phys 6, 659–662 (2010). https://doi.org/10.1038/nphys1734
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1734
This article is cited by
-
Strong majorization uncertainty relations and experimental verifications
npj Quantum Information (2023)
-
Negativity vs. purity and entropy in witnessing entanglement
Scientific Reports (2023)
-
Manipulating the measured uncertainty under Lee-Yang dephasing channels through local \({\cal P}{\cal T}\)-symmetric operations
Frontiers of Physics (2023)
-
Comparing the quantum memory-assisted entropic uncertainties of spin-qubit in presence of spin-qutrit and spin-qubit quantum memories in Heisenberg spin chains
Quantum Information Processing (2023)
-
Quantum Brascamp–Lieb Dualities
Communications in Mathematical Physics (2023)