Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Non-local observables and lightcone-averaging in relativistic thermodynamics

Nature Physics volume 5, pages 741–747 (2009)Cite this article

Abstract

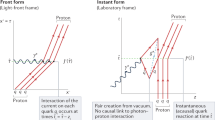
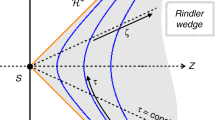
The unification of relativity and thermodynamics has been a subject of considerable debate over the past 100 years. The reasons for this are twofold. First, thermodynamic variables are non-local quantities and therefore single out a preferred class of hyperplanes in spacetime. Second, there exist different ways of defining heat and work in relativistic systems and all of them seem equally plausible. These ambiguities have led, for example, to various proposals for the Lorentz-transformation law of temperature. However, traditional ‘isochronous’ formulations of relativistic thermodynamics are neither theoretically satisfactory nor experimentally feasible. Here, we demonstrate how these deficiencies can be resolved by defining thermodynamic quantities with respect to the backward-lightcone of an observation event. This approach yields new predictions that are, in principle, testable and allows for a straightforward extension of thermodynamics to general relativity. Our theoretical considerations are illustrated through three-dimensional relativistic many-body simulations.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Non-local thermodynamic quantities depend on the underlying hypersurface in Minkowski spacetime.
Figure 2: Equilibrium energy distribution of relativistic gas particles in the lab frame.
Figure 3: Temperature-induced apparent drift effect as seen by a resting observer (w=0).
Figure 4: Photographic energy and momentum estimates for relativistic gases depend sensitively on both the observer velocity and the observer position.

Similar content being viewed by others

References

  1. Callen, H. B. Thermodynamics as a science of symmetry. Found. Phys. 4, 423–442 (1974).

    Article  ADS  Google Scholar 

  2. Callen, H. B. Thermodynamics and an Introduction to Thermostatistics 2nd edn (Wiley, 1985).

    MATH  Google Scholar 

  3. Landau, L. D. & Lifshitz, E. M. Statistical Physics 3rd edn (Course of Theoretical Physics, Vol. 5, Butterworth-Heinemann, 2003).

    MATH  Google Scholar 

  4. Öttinger, H. C. Beyond Equilibrium Thermodynamics (Wiley–IEEE, 2005).

    Book  Google Scholar 

  5. Lloyd, S. Quantum thermodynamics: Excuse our ignorance. Nature Phys. 2, 727–728 (2006).

    Article  ADS  Google Scholar 

  6. Bekenstein, J. D. Black holes and entropy. Phys. Rev. D 7, 2333–2346 (1973).

    Article  ADS  MathSciNet  Google Scholar 

  7. Planck, M. Zur Dynamik bewegter Systeme. Ann. Phys. (Leipz.) 26, 1–34 (1908).

    Article  ADS  Google Scholar 

  8. Einstein, A. Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen. J. Radioaktivität Elektronik 4, 411–462 (1907).

    ADS  Google Scholar 

  9. Van Kampen, N. G. Relativistic thermodynamics of moving systems. Phys. Rev. 173, 295–301 (1968).

    Article  ADS  Google Scholar 

  10. Ott, H. Lorentz-Transformation der Wärme und der Temperatur. Z. Phys. 175, 70–104 (1963).

    Article  ADS  Google Scholar 

  11. Landsberg, P. T. Does a moving body appear cool? Nature 212, 571–572 (1966).

    Article  ADS  Google Scholar 

  12. Landsberg, P. T. Does a moving body appear cool? Nature 214, 903–904 (1967).

    Article  ADS  Google Scholar 

  13. Ter Haar, D. & Wergeland, H. Thermodynamics and statistical mechanics on the special theory of relativity. Phys. Rep. 1, 31–54 (1971).

    Article  ADS  Google Scholar 

  14. Komar, A. Relativistic temperature. Gen. Rel. Grav. 27, 1185–1206 (1995).

    Article  ADS  MathSciNet  Google Scholar 

  15. Dunkel, J. & Hänggi, P. Relativistic Brownian motion. Phys. Rep. 471, 1–73 (2009).

    Article  ADS  MathSciNet  Google Scholar 

  16. Yuen, C. K. Lorentz transformation of thermodynamic quantities. Am. J. Phys. 38, 246–252 (1970).

    Article  ADS  Google Scholar 

  17. Pryce, M. H. L. The mass-centre in the restricted theory of relativity and its connexion with the quantum theory of elementary particles. Proc. R. Soc. Lond. 195, 62–81 (1948).

    Article  ADS  MathSciNet  Google Scholar 

  18. Gamba, A. Physical quantities in different reference systems according to relativity. Am. J. Phys. 35, 83–89 (1967).

    Article  ADS  Google Scholar 

  19. Amelino-Camelia, G. Relativity: Still special. Nature 450, 801–803 (2007).

    Article  ADS  Google Scholar 

  20. Jüttner, F. Das Maxwellsche Gesetz der Geschwindigkeitsverteilung in der Relativtheorie. Ann. Phys. (Leipz.) 34, 856–882 (1911).

    Article  ADS  Google Scholar 

  21. Cubero, D., Casado-Pascual, J., Dunkel, J., Talkner, P. & Hänggi, P. Thermal equilibrium and statistical thermometers in special relativity. Phys. Rev. Lett. 99, 170601 (2007).

    Article  ADS  Google Scholar 

  22. Abramowitz, M. & Stegun, I. A. (eds) Handbook of Mathematical Functions (Dover, 1972).

  23. Van Kampen, N. G. Lorentz-invariance of the distribution in phase space. Physica 43, 244–262 (1969).

    Article  ADS  Google Scholar 

  24. Debbasch, F. Equilibrium distribution function of a relativistic dilute perfect gas. Physica A 387, 2443–2454 (2007).

    Article  ADS  MathSciNet  Google Scholar 

  25. Cercignani, C. & Kremer, G. M. The Relativistic Boltzmann Equation: Theory and Applications (Progress in Mathematical Physics, Vol. 22, Birkhäuser, 2002).

    Book  Google Scholar 

  26. Campisi, M. Thermodynamics with generalized ensembles: The class of dual orthodes. Physica A 385, 501–517 (2007).

    Article  ADS  MathSciNet  Google Scholar 

  27. Liu, C. Einstein and relativistic thermodynamics. Br. J. Hist. Sci. 25, 185–206 (1992).

    Article  MathSciNet  Google Scholar 

  28. Liu, C. Is there a relativistic thermodynamics? A case study in the meaning of special relativity. Stud. Hist. Phil. Sci. 25, 983–1004 (1994).

    Article  Google Scholar 

  29. Van Kampen, N. G. Relativistic thermodynamics. J. Phys. Soc. Jpn 26 (Suppl.), 316–321 (1969).

    ADS  Google Scholar 

  30. Arzelies, H. Transformation relativiste de la temperature et de quelques autres grandeurs thermodynamiques. Nuovo Cimento. 35, 792–804 (1965).

    Article  Google Scholar 

  31. Arzelies, H. Sur le concept de temperature en thermodynamique relativiste et en thermodynamique statistique. Nuovo Cimento. B 40, 333–344 (1965).

    Article  ADS  Google Scholar 

  32. Eddington, A. S. The Mathematical Theory of Relativity (Univ. Press Cambridge, 1923).

    MATH  Google Scholar 

  33. Misner, C. W., Thorne, K. S. & Wheeler, J. A. Gravitation 23rd edn (W. H. Freeman, 2000).

    Google Scholar 

  34. Weinberg, S. Gravitation and Cosmology (Wiley, 1972).

    Google Scholar 

  35. Bennett, C. L. Cosmology from start to finish. Nature 440, 1126–1131 (2006).

    Article  ADS  Google Scholar 

  36. Marra, V., Kolb, E. W. & Matarrese, S. Lightcone-averages in a Swiss-cheese universe. Phys. Rev. D 77, 023003 (2008).

    Article  ADS  Google Scholar 

  37. Wheeler, J. A. & Feynman, R. P. Classical electrodynamics in terms of direct interparticle action. Rev. Mod. Phys. 21, 425–433 (1949).

    Article  ADS  Google Scholar 

  38. Currie, D. G., Jordan, T. F. & Sudarshan, E. C. G. Relativistic invariance and Hamiltonian theories of interacting particles. Rev. Mod. Phys. 35, 350–375 (1963).

    Article  ADS  MathSciNet  Google Scholar 

  39. Montakhab, A., Ghodrat, M. & Barati, M. Statistical thermodynamics of a two dimensional relativistic gas. Phys. Rev. E 79, 031124 (2009).

    Article  ADS  Google Scholar 

  40. Berges, J. Introduction of nonequilibrium quantum field theory. AIP Conf. Proc. 739, 3–62 (2004).

    Article  ADS  Google Scholar 

  41. Hakim, R. Remarks on relativistic statistical mechanics I. J. Math. Phys. 8, 1315–1344 (1965).

    Article  ADS  Google Scholar 

  42. Sexl, R. U. & Urbantke, H. K. Relativity, Groups, Particles (Springer, 2001).

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Rudolf Peierls Centre for Theoretical Physics, University of Oxford, 1 Keble Road, Oxford OX1 3NP, UK

    Jörn Dunkel

  2. Institut für Physik, Universität Augsburg, Universitätsstraße 1, D-86135 Augsburg, Germany

    Peter Hänggi

  3. Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, D-53121 Bonn, Germany

    Stefan Hilbert

Authors
  1. Jörn Dunkel
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Peter Hänggi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Stefan Hilbert
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

J.D. carried out the analytical calculations and S.H. conducted the numerical simulations. All three authors contributed extensively to discussions of the content and to writing the paper.

Corresponding author

Correspondence to Jörn Dunkel.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dunkel, J., Hänggi, P. & Hilbert, S. Non-local observables and lightcone-averaging in relativistic thermodynamics. Nature Phys 5, 741–747 (2009). https://doi.org/10.1038/nphys1395

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphys1395

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing