Abstract
Complex electronic matter shows subtle forms of self-organization, which are almost invisible to the available experimental tools. One prominent example is provided by the heavy-fermion material URu2Si2. At high temperature, the 5f electrons of uranium carry a very large entropy. This entropy is released at 17.5 K by means of a second-order phase transition1 to a state that remains shrouded in mystery, termed a ‘hidden order’ state2. Here, we develop a first-principles theoretical method to analyse the electronic spectrum of correlated materials as a function of the position inside the unit cell of the crystal and use it to identify the low-energy excitations of URu2Si2. We identify the order parameter of the hidden-order state and show that it is intimately connected to magnetism. Below 70 K, the 5f electrons undergo a multichannel Kondo effect, which is ‘arrested’ at low temperature by the crystal-field splitting. At lower temperatures, two broken-symmetry states emerge, characterized by a complex order parameter ψ. A real ψ describes the hidden-order phase and an imaginary ψ corresponds to the large-moment antiferromagnetic phase. Together, they provide a unified picture of the two broken-symmetry phases in this material.
Similar content being viewed by others
Main
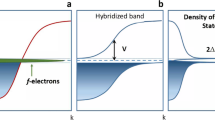
URu2Si2 crystallizes in the body-centred tetragonal structure shown in Fig. 1a. Starting from a localized point of view for U-5f electrons, that is, treating them as core states in density functional theory (DFT) calculations, one obtains a set of wide bands, entirely of s p d character, as shown in Fig. 1b. In an itinerant picture, there are f states close to the Fermi level, which hybridize with the s p d bands to form itinerant states of predominantly f character, with a bandwidth of the order of 1 eV. This is shown in Fig. 1c. This situation is realized in Ce- and Yr-based heavy-fermion materials, the electronic states of which are well described by narrowing the bands of the DFT by a factor of 10–1,000, to account for the heavy mass3.
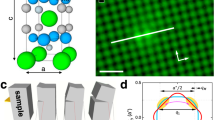
a, Crystal structure of URu2Si2. Gold, grey and blue spheres correspond to U, Ru and Si, respectively. The black rectangle marks the cut of the unit cell for which we show electronic states in Fig. 2. b,c, DFT bands, with U-5f states excluded (b) and U-5f states included in the valence set (c). d, The many-body DMFT electronic structure showing the arrested Kondo effect phenomena. The vertical axis shows the energy ([−200 meV,200 meV] around the Fermi level) and the horizontal axis shows the momentum (around Γ). The light s p d bands are plotted by blue lines, and the bright colours correspond to the U-f spectrum. The temperature in d is T=19 K and the colour coding is the projection of the total electronic spectrum to the U-5f character.
For URu2Si2, we propose a new scenario for the transfer of atomic f weight to the itinerant carriers, which we name the ‘arrested Kondo effect’. At high temperatures, above the characteristic coherence temperature T*∼70 K, the U-5f electrons are localized and do not participate in forming the low-energy bands. The U atoms settle in the 5f2 configuration, for which the crystal environment chooses the non-degenerate atomic ground state. However, the first excited state, which is also non-degenerate, is only Δ=35 K above the ground state, as first observed in polarized neutron scattering experiments4. Hence, in the temperature range Δ<T<T*, the ground state seems doubly degenerate, and hence the Kondo effect develops, leading to the formation of very narrow states near the Fermi energy and a narrow peak in the density of states. The Kondo effect is partially arrested below T<Δ, because the crystal-field splitting between the two singlet states induces a partial gapping at the Fermi level. The situation is shown in Fig. 1c. A non-dispersing slab of f spectral weight is pushed to roughly 8 meV away from the Fermi energy. Although only a small fraction of the f spectral weight is present at the Fermi level, it has a significant effect, resulting in a mass enhancement factor that is over 200 at T=19 K. For temperatures above the crystal-field splitting energy, T∼Δ, the electronic scattering rate is anomalously large. This is a signature of multichannel Kondo physics, whereby the two singlets have the role of the spin in the Kondo problem that scatters degenerate bands. The relevance of the two-channel Kondo physics to U-based impurity models was first proposed by Cox5. Indeed experimental data on dilute UxTh1−xRu2Si2 systems are well described by the two-channel Kondo model6. It is remarkable that the Fermi-liquid regime in URu2Si2 can never be reached. Once the two-channel Kondo effect is arrested by the crystal-field splitting, long-range order, driven by intersite effects, pre-empts the formation of a Fermi-liquid state with a low coherent scale.
The one-electron spectral function A(r,ω) represents the quantum mechanical probability for adding or removing an electron with energy ω at a point r in real space. We calculate it using the combination of the DFT and dynamical mean field theory7 (DMFT)

where χα(r) are the basis functions and Gα β is the electron Green’s function expressed in the basis of χ. More details of the implementation of the DMFT method for this problem are given in the Supplementary Information.
These computational studies are the theoretical counterpart of the scanning tunnelling spectroscopy technique, which has been very useful in describing the properties of numerous correlated materials8 and was very recently applied to URu2Si2 (ref. 9).
The evolution of the electron spectral function A(r,ω) along the cut above the U atom in the unit cell, as depicted in Fig. 1a, is shown in Fig. 2. The curves have an asymmetric line shape of the type

where Γ is the width and q measures the asymmetry of the line shape. These curves were first introduced by Fano10, to describe scattering interference between a discrete state and a degenerate continuum of states. The continuum of states in scanning tunnelling microscopy on URu2Si2 is provided by itinerant s p d bands and the narrow discrete states are the U-5f electronic states, shown with bright colours in Fig. 1d. Notice that the line shape has the most characteristic Fano shape when the position r is on the U or Si atom, with positive asymmetry q>0 on the U atom and negative asymmetry q<0 on the Si atom. With the exception of the small peak, marked with the black arrow in Fig. 2, the line shape on the U atom can be well fitted to the Fano line shape with the parameters q=1.24 and Γ=6.82 meV.
Inset: The calculated electronic density A(r,ω=0) at 20 K, as measured by scanning tunnelling microscopy experiments. We take a representative cut in real space, shown in Fig. 1, which cuts the U muffin-tin sphere at 3/4 height, guaranteeing a large matrix element with the valence 4f-electrons on the U atom. The main panel shows the energy dependence of the electronic density of states at various positions in real space. For each coloured dot we show a curve, of the same colour, in the main panel.
The main features of our calculations, including the characteristic line shape, the width and the strength of the asymmetry of the Fano line shape, as well as the extra small peak around 6 meV, were recently measured in scanning tunnelling experiments by the J.C. Seamus Davis group9, the first experiment of this type on a heavy-fermion system.
To understand the origin of the small peak at 6.8 meV, we integrate the spectrum over the whole unit cell and resolve it in the different angular momentum channels of the different atoms. These orbitally resolved spectra at low energies are shown in Fig. 3a.
a, The total density of electronic states (red) and the orbitally resolved components at T=19 K. Also shown is the U-f component at higher T=50 K. Using the Fermi-liquid estimate for the specific-heat coefficient γ∝A(ω=0)/Z, we obtain γ∼85 mJ mol−1 K−2 at T=50 K (1/Z∼60) and γ∼140 mJ mol−1 K−2 at T=19 K (1/Z∼200). b, The DMFT Fermi surface of URu2Si2 in the paramagnetic state T=20 K>Torder. We take a two-dimensional horizontal cut in the tetragonal body-centred Brillouin zone passing through the origin.
Although there are many Si-3p and Ru-4d states at the Fermi level, these states are only weakly energy dependent in the 200 meV interval. On the other hand, the heavy U-5f electron states have a dip and a peak at the same energy of 6.8 meV, which is clearly visible in the real-space spectra in Fig. 2. Therefore, it is the U-5f non-Lorentzian shape of the electronic density of states that is responsible for the extra peak and the asymmetry variation in the unit cell. This dip–peak line shape is also the key to unravelling the puzzle of the electronic structure of the material, because it shows that instead of a regular Lorentzian Kondo resonance, we have a double peak at low temperature, with a pseudogap at zero energy. This is the signature of the Kondo effect, losing its strength at temperature T below the crystal-field splitting energy T<Δ. Below the ordering temperature (the ordering will be discussed below), the pseudogap in the partial U-5f spectrum is considerably enhanced, as shown in Fig. 3a. Note that owing to mixing of s p d and f states, there is a finite admixture of U-5f states at the Fermi level, giving some ‘heaviness’ to the quasiparticle even below the ordering temperature.
The electronic states can also be resolved in momentum space by computing the spectral function A(k,ω). The active state at the Fermi level, given by peaks of A(k,ω=0), determines the Fermi surface of the material, which is shown in Fig. 3b.
For many Ce-based heavy-fermion compounds, the Fermi surface of the itinerant DFT calculation, as well as that of the DMFT calculation, accounts for the experimentally measured de Haas–van Alphen frequencies. On the other hand, the DMFT Fermi surface of URu2Si2, shown in Fig. 3b, is qualitatively similar to the localized DFT calculation, with 5f states excluded from the valence bands11. Note that Luttinger’s theorem, which counts the number of electrons modulo 2, does not constrain the Fermi surface of the material. Hence, the Fermi surface does not need to resemble the itinerant DFT result.
The first-principles DMFT calculations demonstrate that for URu2Si2 the 5f2 configuration has the dominant weight. This has important consequences, because it allows the physical Fermi surface to have the same volume as a system with no f electrons, such as ThRu2Si2 (ref. 12).
Finally, the DMFT Fermi surface is hole-like, and the large hole Fermi surface centred at Z (where Z is (1,0,0)a*) shows characteristic wave vectors (0.6,0,0)a* and (1.4,0,0)a* shown in Fig. 3b. Recent neutron scattering experiments show low-energy spectral weight at these incommensurate wave vectors13,14,15.
In the long-range order phase, the Fermi surface substantially reconstructs and multiple small electron and hole pockets appear, making this system a compensated metal, with the same number of hole and electron carriers.
The U-5f2 configuration has the total angular momentum J=4 and is split into five singlets and two doublets in the tetragonal crystal environment of URu2Si2. The relative energy of these crystal-field levels is still an open problem and several sequences have been proposed. For a recent review, see ref. 16.
The wavefunctions of the U-5f2 configuration, with the largest weight in the DMFT density matrix, are


Here, |Jz〉=|J=4,J z〉 is a two-particle state of the J=4 multiplet. We obtained φ∼0.23π. The separation between the two singlets is of the order of 35 K. The probability for the atomic ground state,  and the first excited state, |1〉, at 20 K is 0.54 and 0.1, respectively.
and the first excited state, |1〉, at 20 K is 0.54 and 0.1, respectively.
The transition into ordered states requires an understanding of the collective excitations, which are bound states of particle–hole pairs. The identification of the low-lying singlets leads us to consider the following order parameter for URu2Si2

where  is the Hubbard operator, which measures the excitonic mixing between the two lowest-lying U-5f singlets at lattice site Ri.
is the Hubbard operator, which measures the excitonic mixing between the two lowest-lying U-5f singlets at lattice site Ri.
This order parameter is complex. Its real part is proportional to the hexadecapole operator of the A2g irreducible representation of the tetragonal symmetry, Reψ ∝ 〈(JxJy+JyJx)(Jx2−Jy2)〉, introduced in the context of nuclear physics long ago. Its imaginary part is proportional to the magnetization along the z axis, Imψ ∝ 〈Jz〉, which is the only direction allowed within this crystal-field set of states. Experimentally, the moment indeed points in the z direction4.
At low temperatures, we found two different stable DMFT solutions, describing ordered states with non-zero staggered 〈ψ〉 with wave vector Q=(0,0,1). The first solution has 〈ψ〉 purely real and describes the hidden-order phase of URu2Si2. This solution has zero magnetic moment, does not break time-reversal symmetry and has a non-zero hexadecapole. The second DMFT solution has a purely imaginary 〈ψ〉 and we associate this phase with the large-moment antiferromagnet phase, which is experimentally realized at pressures larger than 0.7 GPa (refs 17, 18, 19, 20). Hence, the microscopic approach succeeds in unifying two very distinct broken-symmetry states in a single complex order parameter. The existence of a solution with either purely real or purely imaginary ψ, but without mixtures, indicates a first-order phase transition between these two phases, as observed in the pressure experiments of refs 17, 18, 19, 20.
It is useful to visualize the meaning of this order parameter in a limiting case of a simple atomic wavefunction, where it takes the form  . The average magnetic moment of the ground state is hence 〈g s|J|g s〉=4cos(φ)sin (2θ)sin(ϕ)*(0,0,1). If ϕ is π/2, we have a phase with large magnetic moment and if ϕ vanishes, the moment vanishes.
. The average magnetic moment of the ground state is hence 〈g s|J|g s〉=4cos(φ)sin (2θ)sin(ϕ)*(0,0,1). If ϕ is π/2, we have a phase with large magnetic moment and if ϕ vanishes, the moment vanishes.
Our theory provides a natural explanation for a large number of experiments, which are very puzzling, when examined from other perspectives and suggests new experiments.
First, it has been advocated phenomenologically that even though the hidden-order phase and the large-moment phase have distinct order parameters, the behaviour of many observables across the transition is remarkably similar. The term adiabatic continuity has been used to describe this situation17,21, but it is not justified on theoretical grounds because the two phases are separated by a first-order phase transition. The proposed order parameter ψi, which unifies the no-moment and large-moment phase, explains why even though the two phases are separated by a first-order phase transition, they are in many respects very similar, for example in the critical temperature and entropy change across the transition.
Second, at the hidden-order transition, a small gap of the order of 10 meV opens in the 5f quasiparticle spectrum, as seen in optical conductivity22, specific heat23, thermal conductivity24 and relaxation rate measurements25,26. On the other hand, the d.c. resistivity continues to decrease at low temperatures27, because it is dominated by the itinerant s p d carriers. This fact is hard to understand in a simple itinerant density wave picture. The f-state gap at low energies is also seen in neutron scattering experiments4,14,15.
Third, unlike DFT calculations28, our approach described a strongly correlated normal state with large entropy and can account for the large specific-heat coefficient in the paramagnetic state of the material.
It has recently been proposed that one can detect hexadecapole order using the resonant X-ray technique29. This would be a direct test of our proposed order parameter. High-resolution angle-resolved photoemission spectroscopy can detect the small kink in the very low-energy spectra (<10 meV) of Fig. 1d, which is a unique signature of the arrested Kondo effect. It would be interesting to control the crystal-field splitting energy Δ. A slight decrease (increase) of Δ, will increase (decrease) the hidden-order transition temperature.
Finally, our results set the stage for understanding the mysterious superconducting transition that takes place at the much lower temperatures (Tc=0.8 K). Hidden order is fertile ground for superconductivity, whereas the large-moment antiferromagnetic phase completely eliminates this instability. Our results suggest that Cooper pairing can take place only when the electrons propagate in the time-reversal symmetric background, but unravelling the precise origin of the superconductivity in this material will require further investigation.
References
Palstra, T. T. M. et al. Superconducting and magnetic transitions in the heavy fermion system URu2Si2 . Phys. Rev. Lett. 55, 2727–2730 (1985).
Tripathi, V., Chandra, P. & Coleman, P. Sleuthing hidden order. Nature Phys. 3, 78–80 (2007).
Allen, J. W. The Kondo resonance in electron spectroscopy. J. Phys. Soc. Jpn 74, 34–48 (2005).
Broholm, C. et al. Magnetic excitations and ordering in the heavy-electron superconductor URu2Si2 . Phys. Rev. Lett. 58, 1467–1470 (1987).
Cox, D. L. Kondo effect in real metals. Phys. Rev. Lett. 59, 1240–1243 (1987).
Amitsuka, H. & Sakakibara, T. Single uranim site properties of the dilute heavy electron system UxTh1−xRu2Si2 . J. Phys. Soc. Jpn 63, 736–747 (1994).
Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865–951 (2006).
Kohsaka, Y. et al. How Cooper pairs vanish approaching the Mott insulator in Bi2Sr2CaCu2O8, approaching the Mott insulator. Nature 454, 1072–1078 (2008).
Schmidt, A. et al. Abstract number: BAPS.2009.MAR.V29.3, APS March Meeting, Pittsburgh (2009).
Fano, U. Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 124, 1866–1878 (1961).
Denlinger, J. D. et al. Temperature dependent 5f states in URu2Si2 . J. Electron Spectrosc. Relat. Phenom. 117–118, 347–369 (2001).
Denlinger, J. D. et al. Abstract number: BAPS.2009.MAR.Q2.2, APS March Meeting, Pittsburgh (2009).
Broholm, C. et al. Magnetic excitations in heavy fermion superconductors. Phys. Rev. B 43, 12809–12822 (1991).
Villaume, A. et al. Signature of hidden order in heavy fermion superconductor URu2Si2: Resonance at the wave vector Q0=(1,0,0). Phys. Rev. B 78, 012504 (2008).
Wiebe, C. R. et al. Gapped itinerant spin excitations account for missing entropy in the hidden-order state of URu2Si2 . Nature Phys. 3, 96–99 (2007).
Kiss, A. & Fazekas, P. Group theory and octupolar order in URu2Si2 . Phys. Rev. B 71, 054415 (2005).
Pfleiderer, C., Mydosh, J. A. & Vojta, M. Pressure dependence of the magnetization of URu2Si2 . Phys. Rev. B 74, 104412 (2006).
Amitsuka, H. et al. Pressure–temperature phase diagram of the heavy-electron superconductor URu2Si2 . J. Magn. Magn. Mater. 310, 214–220 (2007).
Motoyama, G. et al. Electrical resistivity and thermal expansion measurements of URu2Si2 under pressure. J. Phys. Soc. Jpn 77, 123710 (2008).
Hassinger, E. et al. Temperature–pressure phase diagram of URu2Si2 from resistivity measurements and ac calorimetry: Hidden order and Fermi-surface nesting. Phys. Rev. B 77, 115117 (2008).
Jo, Y. J. et al. Field-induced Fermi surface reconstruction and adiabatic continuity between antiferromagnetism and the hidden-order state in URu2Si2 . Phys. Rev. Lett. 98, 166404 (2007).
Bonn, D. A., Garret, J. D. & Timusk, T. Far infrared properties of URu2Si2 . Phys. Rev. Lett. 61, 1305–1308 (1988).
van Dijk, N. H. et al. Specific heat of heavy-fermion URu2Si2 in high magnetic fields. Phys. Rev. B 56, 14493–14498 (1997).
Behnia, K. et al. Thermal transport in the hidden-order state of URu2Si2 . Phys. Rev. Lett. 94, 156405 (2005).
Matsuda, K. et al. Spatially inhomogeneous development of antiferromagnetism in URu2Si2: Evidence from 29Si NMR under pressure. Phys. Rev. Lett. 87, 087203 (2001).
Maple, M. B. et al. Partially gapped Fermi surface in the heavy-electron superconductor URu2Si2 . Phys. Rev. Lett. 56, 185–188 (1986).
Schoenes, J. et al. Hall-effect and resistivity study of the heavy-fermion system URu2Si2 . Phys. Rev. B 35, 5375–5378 (1987).
Elgazzar, S. et al. Hidden order in URu2Si2 originates from Fermi surface gapping induced by dynamic symmetry breaking. Nature Mater. 8, 337–341 (2009).
Kuramoto, Y., Kusunose, H. & Kiss, A. Diffraction from ordered states of higher multipoles. Physica B 383, 5–8 (2006).
Acknowledgements
We are grateful to J. Allen, J. Denlinger and J.C. Seamus Davis for fruitful discussion and for sharing unpublished work with us. K.H. was supported by grant NSF DMR-0746395 and an Alfred P. Sloan fellowship. G.K. was supported by NSF DMR-0906943.
Author information
Authors and Affiliations
Contributions
K.H. and G.K. both developed the LDA+DMFT methodology and the physical interpretation of the results.
Corresponding author
Supplementary information
Supplementary Information
Supplementary Information (PDF 227 kb)
Rights and permissions
About this article
Cite this article
Haule, K., Kotliar, G. Arrested Kondo effect and hidden order in URu2Si2. Nature Phys 5, 796–799 (2009). https://doi.org/10.1038/nphys1392
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1392
This article is cited by
-
Non-collinear magnetism driven by a hidden multipolar order in PrO2
Communications Physics (2024)
-
Probing octupolar hidden order via Janus impurities
npj Quantum Materials (2023)
-
Proximity to a critical point driven by electronic entropy in URu2Si2
npj Quantum Materials (2021)
-
Chiral superconductivity in heavy-fermion metal UTe2
Nature (2020)
-
Unveiling hidden multipolar orders with magnetostriction
Nature Communications (2019)