Abstract
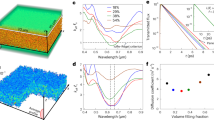
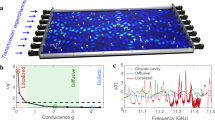
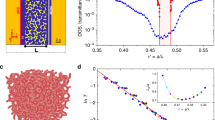
Diffusive wave transport in three-dimensional media should show a phase transition, with increasing disorder, to a state without transport. This transition was first discussed by Anderson1 in the context of the metal–insulator transition, but is generic for all waves, as was realized later2,3. However, the quest for the experimental demonstration of ‘Anderson’ localization in three dimensions has been a challenging task. For electrons4 and cold atoms5,6, the challenge lies in the possibility of bound states in a disordered potential. Therefore, electromagnetic and acoustic waves have been the prime candidates for the observation of Anderson localization7,8,9,10,11,12,13,14,15,16,17. The main challenge in using light lies in the distinction between the effects of absorption and localization11,12. Here, we present measurements of the time dependence of the transverse width of the transmitted-light intensity distribution, which provides a direct measure of the localization length, independent of absorption. This provides direct evidence for a localization transition in three dimensions.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



 of the plateau versus kl* for different samples.
of the plateau versus kl* for different samples.

Similar content being viewed by others
References
Anderson, P. W. Absence of diffusion in certain random lattices. Phys. Rev. 109, 1492–1505 (1958).
Anderson, P. W. The question of classical localization: a theory of white paint? Phil. Mag. Lett. 52, 505–509 (1985).
John, S. Electromagnetic absorption in a disordered medium near a photon mobility edge. Phys. Rev. Lett. 53, 2169–2172 (1984).
Altshuler, B. L. et al. Mesoscopic Phenomena in Solids (North-Holland, 1991).
Kondov, S. S. et al. Three-dimensional Anderson localization of ultracold matter. Science 334, 66–68 (2011).
Jendrzejewski, F. et al. Three-dimensional localization of ultracold atoms in an optical disordered potential. Nature Phys. 8, 398–403 (2012).
Kuga, Y. & Ishimaru, A. Retroreflectance from a dense distribution of spherical particles. J. Opt. Soc. Am. A 1, 831–835 (1984).
van Albada, M. P. & Lagendijk, A. Observation of weak localization of light in a random medium. Phys. Rev. Lett. 55, 2692–2695 (1985).
Wolf, P. E. & Maret, G. Weak localization and coherent backscattering of photons in disordered media. Phys. Rev. Lett. 55, 2696–2699 (1985).
Drake, J. M. & Genack, A. Z. Observation of nonclassical optical diffusion. Phys. Rev. Lett. 63, 259–262 (1989).
Wiersma, D. S., Bartolini, P., Lagendijk, A. & Righini, R. Localization of light in a disordered medium. Nature 390, 671–673 (1997).
Scheffold, F., Lenke, R., Tweer, R. & Maret, G. Localization or classical diffusion of light? Nature 398, 206–270 (1999).
Fiebig, S. et al. Conservation of energy in coherent backscattering at large angles. Europhys. Lett. 81, 64004 (2008).
Störzer, M., Gross, P., Aegerter, C. M. & Maret, G. Observation of the critical regime in the approach to Anderson localization of light. Phys. Rev. Lett. 96, 063904 (2006).
Aegerter, C. M., Störzer, M. & Maret, G. Experimental determination of critical exponents in Anderson localization of light. Europhys. Lett. 75, 562–568 (2006).
Bayer, G. & Niederdränk, T. Weak localization of acoustic waves in strongly scattering media. Phys. Rev. Lett. 70, 3884–3887 (1993).
Hu, H., Strybulevych, A., Page, J. H., Skipetrov, S. E. & van Tiggelen, B. A. Localization of ultrasound in a three-dimensional elastic network. Nature Phys. 4, 945–948 (2008).
Lenke, R. & Maret, G. Multiple Scattering of Light: Coherent Backscattering and Transmission (Gordon & Breach, 2000).
Abrahams, E., Anderson, P. W., Licciardello, D. C. & Ramakrishnan, T. V. Scaling theory of localization: absence of quantum diffusion in two dimensions. Phys. Rev. Lett. 42, 673–676 (1979).
Ioffe, A. F. & Regel, A. R. Non-crystalline, amorphous and liquid electronic semiconductors. Prog. Semicond. 4, 237–291 (1960).
Berkovits, R. & Kaveh, M. Propagation of waves through a slab near the Anderson transition: a local scaling approach. J. Phys. C 2, 307–321 (1990).
Skipetrov, S. E. & van Tiggelen, B. A. Dynamics of Anderson localization in open 3D media. Phys. Rev. Lett. 96, 043902 (2006).
Cherroret, N., Skipetrov, S. E. & van Tiggelen, B. A. Transverse confinement of waves in random media. Phys. Rev. E 82, 056603 (2010).
Gross, P. et al. A precise method to determine the angular distribution of backscattered light to high angles. Rev. Sci. Instrum. 78, 033105 (2007).
Gentilini, S., Fratalocchi, A. & Conti, C. Signatures of Anderson localization excited by an optical frequency comb. Phys. Rev. B. 81, 014209 (2010).
MacKinnon, A. & Kramer, B. One-parameter scaling of localization length and conductance in disordered systems. Phys. Rev. Lett. 47, 1546–1549 (1981).
Acknowledgements
This work was funded by Deutsche Forschungsgemeinschaft, Swiss National Science Foundation and the Land Baden-Württemberg via the Center for Applied Photonics. The authors thank N. Cherroret for support and fruitful discussions.
Author information
Authors and Affiliations
Contributions
T.S., W.B., C.M.A. and G.M. conceived and designed the experiments. T.S. and W.B. carried out the experiments. T.S., W.B., C.M.A. and G.M. analysed and interpreted the data. T.S., W.B., C.M.A. and G.M. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 588 kb)
Rights and permissions
About this article
Cite this article
Sperling, T., Bührer, W., Aegerter, C. et al. Direct determination of the transition to localization of light in three dimensions. Nature Photon 7, 48–52 (2013). https://doi.org/10.1038/nphoton.2012.313
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2012.313
This article is cited by
-
Anderson localization of electromagnetic waves in three dimensions
Nature Physics (2023)
-
Observation of a transition to a localized ultrasonic phase in soft matter
Communications Physics (2022)
-
Exact mobility edges and topological phase transition in two-dimensional non-Hermitian quasicrystals
Science China Physics, Mechanics & Astronomy (2022)
-
Observation of two-dimensional Anderson localisation of ultracold atoms
Nature Communications (2020)
-
Transition from light diffusion to localization in three-dimensional amorphous dielectric networks near the band edge
Nature Communications (2020)