Abstract
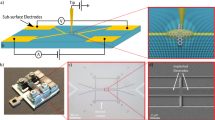
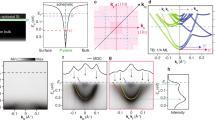
Scaling of Si-based nanoelectronics has reached the regime where device function is affected not only by the presence of individual dopants, but also by their positions in the crystal. Determination of the precise dopant location is an unsolved problem in applications from channel doping in ultrascaled transistors to quantum information processing. Here, we establish a metrology combining low-temperature scanning tunnelling microscopy (STM) imaging and a comprehensive quantum treatment of the dopant–STM system to pinpoint the exact coordinates of the dopant in the Si crystal. The technique is underpinned by the observation that STM images contain atomic-sized features in ordered patterns that are highly sensitive to the STM tip orbital and the absolute dopant lattice site. The demonstrated ability to determine the locations of P and As dopants to 5 nm depths will provide critical information for the design and optimization of nanoscale devices for classical and quantum computing applications.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Ball, P. Feynman's fancy. Chem. World 58, 58–62 (2009).
Fuechsle, M. et al. A single atom transistor. Nature Nanotech. 7, 242–246 (2012).
Weber, B. et al. Ohm's law survives to the atomic scale. Science 335, 64–67 (2012).
Ho, J. et al. Controlled nanoscale doping of semiconductors via molecular monolayers. Nature Mater. 7, 62–67 (2008).
Prati, E. & Shinada, T. Single-Atom Nanoelectronics (Pan Stanford, 2013).
Pierre, M. et al. Single-donor ionization energies in a nanoscale CMOS channel. Nature Nanotech. 5, 133–137 (2010).
Sarkar et al. A subthermionic tunnel field-effect transistor with an atomically thin channel. Nature 526, 91–95 (2015).
Ionescu et al. Tunnel field-effect transistors as energy-efficient electronic switches. Nature 479, 329–337 (2011).
Hill, C. et al. A surface code quantum computer in silicon. Sci. Adv. 1, e1500707 (2015).
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998).
Saeedi, K. et al. Room-temperature quantum bit storage exceeding 39 minutes using ionized donors in silicon-28. Science 342, 830–833 (2013).
Pla, J. et al. High-fidelity readout and control of a nuclear spin qubit in silicon. Nature 496, 334–338 (2013).
Muhonen, J. T. et al. Storing quantum information for 30 seconds in a nanoelectronic device. Nature Nanotech. 9, 986–991 (2014).
Weber, B. et al. Spin blockade and exchange in coulomb-confined silicon double quantum dots. Nature Nanotech. 9, 430–435 (2014).
Tyryshkin, A. et al. Electron spin coherence exceeding seconds in high-purity silicon. Nature Mater. 11, 143–147 (2012).
Dehollain, J. P. et al. Bell's inequality violation with spins in silicon. Nature Nanotech. 11, 242–246 (2016).
Laucht, A. et al. Electrically controlling single-spin qubits in a continuous microwave field. Sci. Adv. 1, e1500022 (2015).
Mohiyaddin, F. et al. Noninvasive spatial metrology of single-atom devices. Nano Lett. 13, 1903–1909 (2013).
Garleff, J. K. et al. Atomically precise impurity identification and modification on the manganese doped GaAs(110) surface with scanning tunneling microscopy. Phys. Rev. B 78, 075313 (2008).
Marczinowski, F. et al. Effect of charge manipulation on scanning tunneling spectra of single Mn acceptors in InAs. Phys. Rev. B 77, 115318 (2008).
Salfi, J. et al. Spatially resolving valley quantum interference of a donor in silicon. Nature Mater. 13, 605–610 (2014).
Saraiva, A. L. et al. Donor wave functions in Si gauged by STM images. Phys. Rev. B 93, 045303 (2015).
Klymenko, M. V. et al. Multivalley envelope function equations and effective potentials for phosphorus impurity in silicon. Phys. Rev. B 92, 195302 (2015).
Usman, M. et al. Strain and electric field control of hyperfine interactions for donor spin qubits in silicon. Phys. Rev. B 91, 245209 (2015).
Rahman, R. et al. High precision quantum control of single donor spins in silicon. Phys. Rev. Lett. 99, 036403 (2007).
Chen, C. J. Tunneling matrix elements in three-dimensional space: the derivative rule and the sum rule. Phys. Rev. B 42, 8841 (1990).
Miwa, J. A., Mol, J. A., Salfi, J., Rogge, S. S. & Simmons, M. Y. Transport through a single donor in p-type silicon. Appl. Phys. Lett. 103, 043106 (2013).
Keizer, J. G. et al. The impact of dopant segregation on the maximum carrier density in Si:P multilayers. ACS Nano 9, 7080–7084 (2015).
Voisin, B., Salfi, J., Bocquel, J., Rahman, R. & Rogge, S. Spatially resolved resonant tunneling on single atoms in silicon. J. Phys. Condens. Matter 27, 154203 (2015).
Boykin, T. B., Klimeck, G. & Oyafuso, F. Valence band effective-mass expressions in the sp3d5s* empirical tight-binding model applied to a Si and Ge parametrization. Phys. Rev. B 69, 115201 (2004).
Usman, M. et al. Donor hyperfine Stark shift and the role of central-cell corrections in tight-binding theory. J. Phys. Condens. Matter 27, 154207 (2015).
Craig, B. I. & Smith, P. V. The structure of the Si(100)2 × 1: H surface. Surf. Sci. 226, L55–L58 (1990).
Lee, S., Oyafuso, F., von Allmen, P. & Klimeck, G. Boundary conditions for the electronic structure of finite-extent embedded semiconductor nanostructures. Phys. Rev. B 69, 045316 (2004).
Bardeen, J. Tunnelling from a many-particle point of view. Phys. Rev. Lett. 6, 57 (1961).
Slater, J. C. Atomic shielding constants. Phys. Rev. 36, 57 (1930).
Chaika, A. N. et al. Selecting the tip electron orbital for scanning tunneling microscopy imaging with sub-angstrom lateral resolution. Eur. Phys. Lett. 92, 46003 (2010).
Teobaldi, G., Inami, E., Kanasaki, J., Tanimura, K. & Shluger, A. L. Role of applied bias and tip electronic structure in the scanning tunneling microscopy imaging of highly oriented pyrolytic graphite. Phys. Rev. B 85, 085433 (2012).
Rahman, R. et al. Engineered valley–orbit splittings in quantum-confined nanostructures in silicon. Phys. Rev. B 83, 195323 (2011).
Salfi, J. et al. Quantum simulation with dopant atoms in a semiconductor. Nature Commun. 7, 11342 (2016).
Mol, J. A., Salfi, J., Miwa, J. A., Simmons, M. Y. & Rogge, S. S. Interplay between quantum confinement and dielectric mismatch for ultrashallow dopants. Phys. Rev. B 87, 245417 (2013).
Averin, D., Korotkov, A. & Likharev, K. Theory of single-electron charging of quantum wells and dots. Phys. Rev. B 44, 6199–6211 (1991).
Pitters, J. L., Piva, P. G. & Wolkow, R. A. Dopant depletion in the near surface region of thermally prepared silicon (100) in UHV. J. Vac. Sci. Technol. B 30, 021806 (2012).
Lee, D.-H. & Gupta, J. A. Tunable field control over the binding energy of single dopants by a charged vacancy in GaAs. Science 330, 1807–1810 (2010).
Teichmann, K. et al. Controlled charge switching on a single donor with a scanning tunneling microscope. Phys. Rev. Lett. 101, 076103 (2008).
Ahmed, S. et al. in Encyclopedia of Complexity and Systems Science (ed. Meyers, R.) 5745–5783 (Springer, 2009).
Klimeck, G. et al. Atomistic simulation of realistically sized nanodevices using NEMO 3-D—part II: Models and benchmarks. IEEE Trans. Electron. Dev. 54, 2090–2099 (2007).
Acknowledgements
This work is funded by the Australian Research Council Center of Excellence for Quantum Computation and Communication Technology (CE110001027) and in part by the US Army Research Office (W911NF-08-1-0527). M.Y.S. acknowledges an ARC Laureate Fellowship. This work is supported by the European Commission Future and Emerging Technologies Proactive Project MULTI (317707). Computational resources are acknowledged from NCN/Nanohub. M.U. thanks C. Hill and V. Perunicic for discussions.
Author information
Authors and Affiliations
Contributions
L.C.L.H. and M.U. formulated the theoretical framework for the metrology scheme, including tight-binding calculations of the STM images with generic tip orbitals with input from J.S. M.U. performed the theoretical calculations. J.B., J.S., B.V., M.Y.S. and S.R. designed and conducted the STM measurements. L.C.L.H. and M.U. wrote the manuscript with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 2556 kb)
Rights and permissions
About this article
Cite this article
Usman, M., Bocquel, J., Salfi, J. et al. Spatial metrology of dopants in silicon with exact lattice site precision. Nature Nanotech 11, 763–768 (2016). https://doi.org/10.1038/nnano.2016.83
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nnano.2016.83
This article is cited by
-
Hydrogenic spin-valley states of the bromine donor in 2H-MoTe2
Communications Physics (2023)
-
A solid-state quantum microscope for wavefunction control of an atom-based quantum dot device in silicon
Nature Electronics (2023)
-
Scanning tunneling microscopy of buried dopants in silicon: images and their uncertainties
npj Computational Materials (2022)
-
Scanning probe microscopy
Nature Reviews Methods Primers (2021)
-
Framework for atomic-level characterisation of quantum computer arrays by machine learning
npj Computational Materials (2020)