Abstract
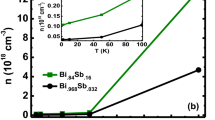
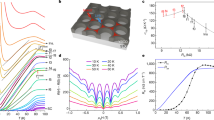
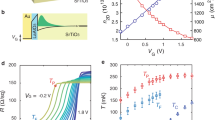
Ohm’s law is a fundamental paradigm in the electrical transport of metals1. Any transport signatures violating Ohm’s law would give an indisputable fingerprint for a novel metallic state. Here, we uncover the breakdown of Ohm’s law owing to a topological structure of the chiral anomaly in the Weyl metal phase. We observe nonlinear I–V characteristics in Bi0.96Sb0.04 single crystals in the diffusive limit, which occurs only for a magnetic-field-aligned electric field (E∥B). The Boltzmann transport theory with the charge pumping effect reveals the topological-in-origin nonlinear conductivity, and it leads to a universal scaling function of the longitudinal magnetoconductivity, which completely describes our experimental results. As a hallmark of Weyl metals, the nonlinear conductivity provides a venue for nonlinear electronics, optical applications, and the development of a topological Fermi-liquid theory beyond the Landau Fermi-liquid theory.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Ohm, G. S. Die galvanische Kette, mathematisch bearbeitet (TH Riemann, 1827).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–1976 (2010).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539 (2010).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011).
Nielsen, H. B. & Ninomiya, M. The Adler-Bell-Jackiw anomaly and Weyl fermions in a crystal. Phys. Lett. 130B, 389 (1983).
Kim, K.-S., Kim, H.-J., Sasaki, M., Wang, J.-F. & Li, L. Anomalous transport phenomena in Weyl metal beyond the Drude model for Landau’s Fermi liquids. Sci. Technol. Adv. Mater. 15, 064401 (2014).
Hosur, P. & Qi, X. L. Recent developments in transport phenomena in Weyl semimetals. C. R. Phys. 14, 857 (2013).
Haldane, F. D. M. Berry curvature on the Fermi surface: anomalous Hall effect as a topological Fermi-liquid property. Phys. Rev. Lett. 93, 206602 (2004).
Murakami, S. Phase transition between the quantum spin Hall and insulator phases in 3D: emergence of a topological gapless phase. New J. Phys. 9, 356 (2007).
Burkov, A. A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).
Kim, H.-J. et al. Dirac versus Weyl fermions in topological insulators: Adler-Bell-Jackiw anomaly in transport phenomena. Phys. Rev. Lett. 111, 246603 (2013).
Xiong, J. et al. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 350, 413–416 (2015).
Li, C. et al. Giant negative magnetoresistance induced by the chiral anomaly in individual Cd3As2 nanowires. Nat. Commun. 6, 10137 (2015).
Liang, T. et al. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2 . Nat. Mater. 14, 280 (2015).
Li, H. et al. Negative magnetoresistance in the Dirac semimetal Cd3As2 . Nat. Commun. 7, 10301 (2016).
Arnold, F. et al. Negative magnetoresistance without well-defined chirality in the Weyl semimetal TaP. Nat. Commun. 7, 11615 (2016).
Huang, X. et al. Observation of the chiral-anomaly-induced negative magnetoresistance in 3D Weyl semimetal TaAs. Phys. Rev. X 5, 031023 (2015).
Li, Q. et al. Chiral magnetic effect in ZrTe5 . Nat. Phys. 12, 550–554 (2016).
Goswami, P. & Tewari, S. Axionic field theory of (3+1)-dimensional Weyl semimetals. Phys. Rev. B 88, 245107 (2013).
Zyuzin, A. A. & Burkov, A. A. Topological response in Weyl semimetals and the chiral anomaly. Phys. Rev. B 86, 115133 (2012).
Son, D. T. & Spivak, B. Z. Chiral anomaly and classical negative magnetoresistance of Weyl metals. Phys. Rev. B 88, 104412 (2013).
Kim, K.-S., Kim, H.-J. & Sasaki, M. Boltzmann equation approach to anomalous transport in a Weyl metal. Phys. Rev. B 89, 195137 (2014).
Kim, K.-S. Role of axion electrodynamics in a Weyl metal: violation of Wiedemann-Franz law. Phys. Rev. B 90, 121108(R) (2014).
Sharma, G., Goswami, P. & Tewari, S. Nernst and magnetothermal conductivity in a lattice model of Weyl fermions. Phys. Rev. B 93, 035116 (2016).
Son, D. T. & Yamamoto, N. Berry curvature, triangle anomalies, and the chiral magnetic effect in Fermi liquids. Phys. Rev. Lett. 109, 181602 (2012).
Stephanov, M. A. & Yin, Y. Chiral kinetic theory. Phys. Rev. Lett. 109, 162001 (2012).
Manuel, C. & Torres-Rincon, J.-M. Chiral transport equation from the quantum Dirac Hamiltonian and the on-shell effective field theory. Phys. Rev. D 90, 076007 (2014).
Fukushima, K., Kharzeev, D. E. & Warringa, H. J. Chiral magnetic effect. Phys. Rev. D 78, 074033 (2008).
Chen, Y., Wu, S. & Burkov, A. A. Axion response in Weyl semimetals. Phys. Rev. B 88, 125105 (2013).
Jho, Y.-S., Han, J.-H. & Kim, K.-S. Topological Fermi-liquid theory for interacting Weyl metals with time reversal symmetry breaking. Phys. Rev. B 95, 205113 (2017).
Acknowledgements
D.S. and J.K. were supported by the Ministry of Education, Science, and Technology (No. NRF-2017R1A2B4012482) and by the Institute for Basic Science (IBS), Grant No. IBS-R014-D1. D.S. and J.K. are grateful to J. Jeong and H. Chang for TEM measurement. K.-S.K. was supported by the Ministry of Education, Science, and Technology (No. NRF-2015R1C1A1A01051629 and No. 2011-0030046) of the National Research Foundation of Korea (NRF) and by TJ Park Science Fellowship of the POSCO TJ Park Foundation. K.-S.K. was also supported by the POSTECH Basic Science Research Institute Grant (2016). Work at LANL was supported by the National Science Foundation under Grant NSF-DMR-1157490. H.-J.K. was supported by the Basic Science Research Program and National Nuclear R&D Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT, and Future Planning (No. NRF-2014R1A1A1002263, NRF-2011-0031558 (mpk)). Y.L. and Y.H.J. were supported by NRF (2011- 0030786 and 2015R1D1A1A02062239). We would like to acknowledge fruitful discussions in the APCTP Focus programme ‘Lecture series on Beyond Landau Fermi liquid and BCS superconductivity near quantum criticality’ in 2016 and the BK21 plus project.
Author information
Authors and Affiliations
Contributions
J.K. supervised the project. D.S. and K.-S.K. performed the analytical and numerical work. D.S. and Y.L. performed the experiments at low magnetic fields. F.W. and J.B.B. carried out measurements in high pulsed fields at LANL. M.S. made single-crystal samples. D.S., H.-J.K., K.-S.K. and J.K. analysed the data. D.S., H.-J.K., K.-S.K. and J.K. wrote the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1370 kb)
Rights and permissions
About this article
Cite this article
Shin, D., Lee, Y., Sasaki, M. et al. Violation of Ohm’s law in a Weyl metal. Nature Mater 16, 1096–1099 (2017). https://doi.org/10.1038/nmat4965
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat4965
This article is cited by
-
Nonlinear electrical transport phenomena as fingerprints of a topological phase transition in ZrTe5
Communications Materials (2023)
-
Weak antilocalization, spin–orbit interaction, and phase coherence length of a Dirac semimetal Bi0.97Sb0.03
Scientific Reports (2022)
-
Possible permanent Dirac- to Weyl-semimetal phase transition by ion implantation
NPG Asia Materials (2022)
-
Anomalous negative longitudinal magnetoresistance and violation of Ohm's law deep in the topological insulating regime in Bi\(_{1-x}\)Sb\(_x\)
Scientific Reports (2021)
-
Large anomalous Hall current induced by topological nodal lines in a ferromagnetic van der Waals semimetal
Nature Materials (2018)