Abstract
Enhanced coupling of material properties offers new fundamental insights and routes to multifunctional devices. In this context 5d oxides provide new paradigms of cooperative interactions that drive novel emergent behaviour. This is exemplified in osmates that host metal–insulator transitions where magnetic order appears intimately entwined. Here we consider such a material, the 5d perovskite NaOsO3, and observe a coupling between spin and phonon manifested in a frequency shift of 40 cm−1, the largest measured in any material. The anomalous modes are shown to involve solely Os–O interactions and magnetism is revealed as the driving microscopic mechanism for the phonon renormalization. The magnitude of the coupling in NaOsO3 is primarily due to a property common to all 5d materials: the large spatial extent of the ion. This allows magnetism to couple to phonons on an unprecedented scale and in general offers multiple new routes to enhanced coupled phenomena in 5d materials.
Similar content being viewed by others
Introduction
Transition metal oxides with 3d ions host a remarkable variety of intriguing phenomena, such as unconventional superconductivity, multiferroic behaviour, colossal magnetoresistance and the Mott metal–insulator transition (MIT)1. These properties arise from the strong electron correlations and localized orbitals characteristic of 3d ions. Materials with 5d ions reside in an alternative regime of intermediate electron correlations, extended orbitals, enhanced spin-orbit coupling (SOC) and large crystalline electric field splitting. The competition and cooperation of these new sets of interactions can drive the emergence of novel behaviour beyond that possible in 3d-based materials2,3. This is manifested in the insulating states of iridates and osmates. In Sr2IrO4, (ref. 4) and other iridates5,6, a Mott-like insulating state exists due to enhanced SOC creating a half-filled Jeff=1/2 electronic band that can be split by even the reduced on-site Coulomb interactions of 5d ions. Conversely the neighbouring osmate NaOsO3, that we focus on here, is believed to host a Slater MIT with behaviour that falls outside the Mott–Hubbard paradigm successfully employed to describe 3d transition metal oxides7,8,9,10. In the case of a Slater MIT it is the onset of magnetic order and the accompanying creation of a periodic potential that acts as a direct and continuous tuning parameter between metallic and insulating states. The interactions within the 5d3 ion in NaOsO3 appear central to the occurrence of the MIT, with the first proposed three-dimensional Slater candidate Cd2Os2O7 sharing the same 5d3 electronic ground state.
Here we access the collective excitations and fundamental interactions through the Slater MIT in NaOsO3 by probing the phonon modes. Our experimental and theoretical results reveal a high degree of cooperation between the magnetic structure, lattice and electronic conductivity that results in a spin-phonon-electronic coupled transition. The magnitude of the phonon coupling is anomalously large leading us to consider and contrast our results with 3d transition metal oxides, where investigating spin-phonon coupling has proven extremely useful in understanding multiferroics11,12, systems with the same perovskite structure as NaOsO3, as well as in a variety of other systems, including high temperature superconductors13. The largest reported phonon shift in a perovskite is found in (Sr,Ba)MnO3 with a value of Δω=25 cm−1 in the TO1 polar phonon14,15. While the investigations of phonon modes in the context of 5d materials is currently limited, it was recently found that the mixed 3d–5d half-metal double perovskite Ba2FeReO6 hosts a dramatic spin-electron-phonon coupling as evidenced by a phonon shift of Δω=30 cm-1, (ref. 16) the largest ever reported prior to our present work on NaOsO3. The phonon shift in Ba2FeReO6 is reported as being directly linked to the interaction between the 3d and 5d ions. Conversely, we show here that 5d ions alone can produce even larger spin-phonon shifts. By considering the various competing mechanisms in NaOsO3, including the electronic changes at the MIT and structurally driven charge disproportionation, we find the microscopic behaviour to be driven by the G-type magnetic structure that orders in the perovskite structure. The enhanced nature is promoted by the extended orbitals of the 5d ion that supports strong coupling between the magnetic superexchange and phonon vibrations. By contrasting our results with measurements on Cd2Os2O7, that show a much reduced spin-phonon shift, we consider the key ingredients required to achieve even larger spin-phonon coupling in general in further systems.
Results
Measurement of anomalous spin-phonon coupling in NaOsO3
To follow the behaviour of collective excitations in NaOsO3 through the magnetic MIT we performed inelastic neutron scattering (INS) measurements. Figure 1a shows the key result of the temperature dependence of the phonon density of states (pDOS) whose peaks are related to the underlying phonon modes. We focus on the region around 700 cm−1 that covers the essential physics of interest. The full spectrum is shown in Supplementary Fig. 1. Three distinct resolution limited peaks in the pDOS are observed around 700 cm−1 and fitting these each to a Gaussian, as shown in Fig. 1a, allows the energy of the modes to be followed with temperature. The key result of a pronounced phonon frequency shift is observed in Fig. 1a,b. Moreover there is an anomalous and counterintuitive intensity increase with decreasing temperature through the MIT as shown inset Fig. 1a considering the entire range of 550–800 cm−1. The results are significant in several regards. First, the onset of the phonon mode shift is concurrent with the magnetic MIT in NaOsO3 at 410 K, indicating a coupling of the phonons to the magnetic and electronic transitions. Second, the phonons show a shift of Δω=40 cm−1, the largest measured in any material for a spin-phonon coupled transition.
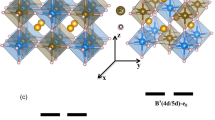
(a) Thermal evolution of the phonon mode density of states measured with inelastic neutron scattering through the magnetic Slater MIT temperature of 410 K. Three modes are resolvable between 550 and 800 cm−1 at all temperatures. The data (filled circles) were modelled (coloured lines) to three Gaussian lineshapes with the width of the energy resolution (∼15 cm−1 full width at half maximum). The three resolvable modes are shown for the 490 K data by the grey dashed lines. The different temperature measurements are shown offset in intensity to aid comparison. The three grey vertical lines indicate the frequencies from the Gaussian fits to the spectra for each temperature. Inset reveals an abnormal intensity increase with decreasing temperature of the integrated intensity over the region 550–800 cm−1. (b) The shaded regions distinguish the low temperature magnetic-insulating and high temperature non-magnetic metallic phases in NaOsO3. The measured phonon mode frequencies obtained from inelastic neutron scattering and (c) from DFT calculations both show strong agreement and reveal a phonon shift at the Slater transition of Δω=40 cm−1. The DFT calculations allow assignment of the responsible modes, as indicated. The breathing modes occur at higher frequencies than the asymmetric stretching, with B2g occurring at the highest frequency. (d) The separate distortions, that all involve Os–O interactions, are shown with the directions indicated by the red arrows. Ag (in phase) and B3g (out of phase) correspond to asymmetric stretching. B1g (in phase) and B2g (out of phase) represent symmetric stretching breathing modes. Error bars throughout the figure represent the s.d. in the data fitting procedure.
To begin to understand the microscopic origin of the behaviour in NaOsO3 we consider the role of the MIT with complimentary neutron measurements on Cd2Os2O7. Cd2Os2O7 was chosen since it has the same 5d3 electronic configuration of the Os5+ ion and hosts a magnetic MIT that is very similar to NaOsO3, with current debate as to whether the mechanism is Slater or Lifshitz17,18. The inelastic neutron measurements through the magnetic MIT in Cd2Os2O7 are shown in Supplementary Fig. 2. While there is an apparent phonon shift at the magnetic transition the value of Δω=4 cm−1 is much reduced from NaOsO3. The disparate results for NaOsO3 and Cd2Os2O7 indicate that the underlying mechanism for the anomalously large behaviour in NaOsO3 cannot be attributed to the occurrence of the MIT, since both host similar MITs with similar energy scales. Instead, as we support with further results and calculations, the microscopic mechanism is related to the magnetic ordering and lattice topology of NaOsO3.
Considering a further pertinent material, the 3d–5d material Ba2FeReO6 that showed a phonon shift of Δω=30 cm−1, we note this occurred concurrent with a structural symmetry change16. No symmetry change has been detected in NaOsO3 (refs 8, 9). However, to explore this possibility further we performed detailed neutron pair density functional measurements through the Slater MIT, see Supplementary Figure 3, and found no local symmetry change. Hence, the enhanced spin-phonon coupling does not appear to arise due to static long or short range lattice distortions in NaOsO3.
Theoretical demonstration of spin-phonon shift
To gain a microscopic insight into the origin of the anomalous phonon mode behaviour in NaOsO3 and disentangle the myriad of competing interactions at the magnetic and electronic transition we performed detailed density functional theory (DFT) calculations. The DFT results show the same three phonon modes observed with INS between 600 to 900 cm−1, see Fig. 1c, and as expected for the orthorhombic structure in NaOsO3 these are themselves composed of three branches, unresolvable in the current powder INS measurement. The theoretical shift is in very close agreement with the measured value of Δω=40 cm−1. This indicates the calculations that probe only the Brillouin zone center accurately reproduce the essential physics of the system as measured by neutrons that probe the entire Brillouin zone. The thermal behaviour was captured in the calculations by increasing the magnetic moment <Si.Sj> to reproduce the onset of G-type antiferromagnetic order in NaOsO3 with the predicted magnetic ordering at 415 K very close to the 411 K observed experimentally. The DFT results, with the need to include magnetism, immediately indicate that the mechanism of the phonon shift is entwined with the onset of magnetic order.
Octahedral B2g breathing mode and charge disproportionation
The calculations reveal all of the phonon modes and are shown in Fig. 1d. They all correspond to Os–O vibrations, specifically breathing modes B1g (in phase) and B2g (out of phase) and two asymmetric Jahn–Teller stretching modes Ag (in phase) and B3g (out of phase). To reveal the role of these modes in NaOsO3 we begin by first considering the static behaviour of the octahedra and propensity towards Jahn–Teller distortion. This can be quantified by introducing parameters Q2 and Q3, which are shown schematically in Fig. 2a, and defined as Q2=(x1−x4−y2+y5)/√2 and Q3=(2z3−2z6−x1+x4−y2+y5)/√6, where x, y and z are the oxygen positions19. Thereby the values of Q2 and Q3 reveals the degree of static octahedral anisotropy, with the larger the value the more distorted the octahedra. Calculations from experimentally determined atomic parameters for NaOsO3 (ref. 9) reveal Q2 and Q3 to be small at all temperatures, but counter intuitively decrease through the Slater MIT. Specifically, at 500 K Q2=0.0114(15) a.u. and at 300 K Q2=0.0035(11) a.u. While at 500 K Q3=0.0171(18) a.u and at 300 K Q3=0.0114(14) a.u. Therefore this reveals that in NaOsO3 the octahedra actually become more isotropic in three dimensions within the low temperature insulating regime. This behaviour is at odds to the normal Jahn–Teller distortions of increased anisotropy and does not favour the asymmetric stretching modes Ag and B3g. Instead the increased static octahedral isotropy is more conducive to the symmetric breathing distortions B1g and B2g. Indeed the abnormal behaviour of the intensity increase of the pDOS, in inset of Fig. 1a, is consistent with an increase in vibration with decreasing temperature, counter to usual thermal behaviour. This appears most pronounced at the highest frequency, which corresponds to the breathing mode B2g and consequently appears central to the behaviour of NaOsO3.
(a) The static octahedral distortion can be quantified with parameters Q2 and Q3 that represent the degree of octahedral anisotropy defined as Q2=(x1−x4−y2+y5)/√2 and Q3=(2z3−2z6−x1+x4−y2+y5)/√6, where x, y and z are the oxygen positions labelled 1−6. The red arrows indicate the directions of Os–O distortions. Unusually Q2 and Q3 both show reduced values below the Slater MIT indicating the octahedra become more isotropic at lower temperature. (b) This counterintuitive behaviour is compatible with the symmetric three-dimensional B2g distortion, depicted by red arrows, increasing in the low temperature insulating regime. The solid lines are DOS calculations for oxygen displacements (u), within the paramagnetic regime, of u=0 Å (black line), u=0.1 Å (magenta line) and u=0.2 Å (red line). For the large oxygen displacement of u=0.2 Å, much beyond that accessed in our measurements, the breathing distortion can open a band gap as revealed in the DOS from DFT calculations. (c) We stress by reproducing published results8 that it is solely the onset of G-type magnetic ordering that opens the gap via the Slater mechanism in NaOsO3. No oxygen displacement, u=0 Å, (black line) shows no gap in the DOS whereas an insulating gap is created for G-type antiferromagnet (AFM) order (blue line). This ordering is indicated by the blue arrows. (d) Although the required u displacement is too large to drive the MIT in NaOsO3, it creates charge disproportionation (δ(e)) on the Os ion. As shown schematically the G-type antiferromagnetic ordering (blue arrows) and periodic expansion/contraction of the B2g breathing mode ordering are isosymmetric in NaOsO3. A consequence of the static ordering of the octahedra, as shown in frozen DFT calculations, is the creation of charge disproportionation, indicated by the creation of +δ and –δ ordering (magenta sphere). The predicted value in NaOsO3, δ(e), is indicated by the blue shaded region.
Considering the B2g mode further we find that sufficiently large breathing distortions of the octahedra, much larger than accessed in our measurements, offers a potential route to opening the insulating gap in the paramagnetic regime, see Fig. 2b. Our frozen DFT results show that in the perovskite structure of NaOsO3 the gap opening can occur since the octahedral breathing causes neighbouring octahedra to expand/contract that in turn creates a periodic charge disproportionation on the Os ion. In addition there is apparent isosymmetric ordering and coupling between the G-type antiferromagnet and octahedral B2g mode ordering (behaviour shown schematically in Fig. 2d). We note that no other phonon distortion produces similar periodic ordering or routes to open a gap. For the B2g mode to create a gap the minimum required oxygen displacement is u=0.2 Å, see Fig. 2b. This corresponds to 10% of the actual Os–O bond distance and therefore it is too large to allow this mechanism to drive the MIT in NaOsO3. However, statically, while not opening a gap the periodic octahedral breathing ordering creates a strong charge disproportionation of Δδ/Δu=7.0 e/Å in the lattice due to the change of the electronic potential around the Os ion and places the system on the verge of a MIT. For example considering a nominal Os–O phonon vibration displacements of the order 0.01 Å as occurring in NaOsO3 then the dynamic charge disproportionation will be ∼0.01e. This indicates that suitable control of the octahedra via pressure or strain is a potential route to tune the MIT in NaOsO3. We stress that, as shown in Fig. 2c that substantiates earlier work8, it is the onset of antiferromagnetic order alone that creates the insulating gap via the Slater mechanism.
Suppressed role of SOC in NaOsO3
While SOC is often attributed to anomalous behaviour of 5d materials, in NaOsO3 the 5d3 t2g-degenerate ground state will suppress the effective SOC20. We nevertheless addressed the role of SOC with X-ray absorption near edge spectroscopy that allows a quantitative comparison with SOC enhanced iridates. As expected our results indicate SOC does not play a dominant role in the behaviour of NaOsO3 as discussed in the Supplementary Material (Supplementary Fig. 4 and Supplementary Note 1). Our first-principle results additionally show the large coupling without SOC.
Coupling of lattice, magnetic order and MIT
The coupled properties in NaOsO3 are illustrated in Fig. 3 where experimentally there is a direct scaling of the structural anomaly of the lattice constants, phonon mode shift, magnetic moment, with the MIT qualitatively following a similar trend. This reveals a high degree of cooperation in NaOsO3 via spin-phonon-electronic coupling. While the realization of numerous overlapping phenomena is currently rare it is likely that additional 5d materials will host similar rich phase diagrams with the prospect of enhanced magnitudes.
The measured temperature dependence of the phonon mode frequency shift (blue square), the [110] magnetic Bragg reflection intensity9 (white square), and the a (black diamond) and c (red triangle) lattice constants in NaOsO3 (altered from ref. 9) show a direct scaling with temperature through the Slater MIT due to spin-phonon-electronic coupling. The lattice parameters have been corrected by removing a constant sloping thermal background. Error bars throughout the figure represent the s.d. in the data fitting procedure. The shaded regions distinguish the low temperature magnetic-insulating and high temperature non-magnetic metallic phases in NaOsO3.
Discussion
We have presented both experimental and theoretical results that show an enhanced phonon shift in NaOsO3, which along with the concurrent magnetic MIT creates a spin-phonon-electronic transition above room temperature. Considering the collective results we argue that the occurrence of the anomalous spin-phonon behaviour is a direct consequence of the extended 5d orbitals coupling to the magnetic structure via the Os–O–Os superexchange interactions on an unprecedented scale and is not driven by the MIT or structural anomalies. The central role of magnetism is emphasized in our DFT calculations that require the inclusion of magnetic order to reproduce the experimental phonon shift. However, as the reduced spin-phonon shift in Cd2Os2O7 attests, the presence of 5d magnetic order alone is not sufficient to induce enhanced coupled phenomena. Instead, within 5d systems, it is not just the onset of magnetic ordering but the specific type of magnetic structure and the lattice it resides on that supports enhanced spin-phonon coupling.
By considering the specific modes in NaOsO3 the B2g breathing mode emerges as central to the behaviour. The mode is characterized by expansion/contraction of neighbouring octahedra that in NaOsO3 can statically order in a periodic way, isosymmetric with the magnetic spins (G-type antiferromagnet), with every nearest neighbouring octahedra oppositely expanded/contracted (see Fig. 2). The breathing mode ordering causes charge disproportionation that grows as the B2g vibrations increase within the low temperature insulating phase and can promote the opening of a charge gap for sufficiently large vibrations. However, the distortion under the experimental conditions we measured falls well short of the value required to drive a MIT via this alternative non-magnetic mechanism in NaOsO3. Instead, once the insulating gap develops via solely the magnetic Slater mechanism, the breathing mode becomes favourable and the structure subtly alters allowing the octahedra to become more isotropic as a route to increase the symmetric breathing mode and consequently enhance the insulating state.
All of the modes uncovered that show an anomalous shift (B1g, B2g, Ag and B3g) are characterized by simultaneous bond-stretching/shrinking between the oxygen and osmium ions of the OsO6 octahedra. Therefore as these modes vibrate they change the O–Os–O wavefunction overlap. Since the magnetism in NaOsO3 is mediate by the superexchange interaction this provides a direct route to couple to the Os–O modes. In the non-magnetic regime the frequency of the Os–O modes do not change, as expected. However, as the magnetic order develops via the Os–O superexchange interactions this couples to the Os–O modes. The degree of the coupling is governed by the 5d(Os)-2p(O) orbital overlap, which is much larger in 5d oxides compared to analogous 3d systems. The consequence is that in NaOsO3 the large wavefunction overlap results in a magnification of the spin-phonon coupling, with the expectation that similar behaviour will be found in further 5d-based systems since the extended orbitals are an intrinsic property. With this expectation for designing 5d materials with strong coupling in mind the reduced spin-phonon coupling in Cd2Os2O7 provides useful insights. The reduced spin-phonon magnitude in Cd2Os2O7 naturally occurs by considering the differences in the lattice topology, specifically the Os–O–Os bond that mediates the emergent behaviour. While the Os–O–Os bond distance is nearly identical in NaOsO3 and Cd2Os2O7 the bond angles diverge. In NaOsO3 it is 155°, whereas in Cd2Os2O7 it is 137°, appreciably further from 180°. Consequently the propagation of …–Os–O–Os–… vibrations throughout the lattice can be sufficiently suppressed within the pyrochlore structure resulting in a reduced coupling of phonons to the magnetic interactions and a smaller, although still finite, spin-phonon coupling. Collectively our results indicate that new cases of similarly enhanced spin-phonon coupling, along with further coupled phenomena, should be found in cubic 5d perovskites with near ideal 180° Os–O–Os bonds.
Methods
Synthesis
Polycrystalline samples of NaOsO3 were prepared using a high pressure solid state synthesis with pressures of 6 GPa, as described in ref. 8. Polycrystalline Cd2Os2O7 was prepared with isotopic 114Cd for neutron measurements to negate the extremely high neutron absorption of standard Cd using sold state techniques from 114CdO and OsO2 powders.
Inelastic neutron scattering
Inelastic neutron scattering measurements were performed on the ARCS and SEQUOIA spectrometers at the spallation neutron source on a 5-g polycrystalline sample of NaOsO3 and 7-g polycrystalline sample of Cd2Os2O7, respectively. The NaOsO3 sample was loaded into a vanadium can and measurements performed between 300 and 500 K using an incident energy of 120 meV. The Cd2Os2O7 sample was measured in an Al can from 150 to 250 K using an incident energy of 100 meV. Corrections for the Bose factor, where appropriate, were performed using the DAVE software21.
DFT
First-principles calculations were performed using density functional theory within the generalized gradient approximation GGA+U method with the Perdew–Becke–Erzenhof parameterization as implemented in the Vienna ab initio Simulation Package (VASP 5.3)22. Theoretical details for spin-phonon coupling are described in ref. 23. We use the Dudarev24 implementation with on-site Coulomb interaction U=1.7 eV and on-site exchange interaction JH=1 eV, so Ueff=0.7 eV to treat the localized d electron states in Os. Within GGA+U, this small U gives excellent agreement between the experimental Neel temperature (TN=411 K) and calculated one (TN,MFT=415 K) in mean-field approximation. The projector augmented wave potentials25 explicitly include 9 valence electrons for Na (2s2 2p6 3s1 ), 14 for Os (5p6 5d5 6s2) and 6 for oxygen (2s2 2p4). To capture spin-phonon coupling with respect to temperature we employed the method successfully used for various magnetic perovskites19,23.
Our calculations use the harmonic approximation throughout. This route is supported by the experimental observation that the peak widths are resolution limit and do not show any broadening that would be associated with anhormonicity.
Neutron pair density function
Neutron pair density functional measurements were performed on the Nanoscale-Ordered Materials Diffractometer (NOMAD) beamline at the spallation neutron source on a powder sample of NaOsO3 from 370 to 460 K. The data were analyzed and modelled with pdfgui26.
X-ray absorption near edge spectroscopy
X-ray absorption measurements were performed at the advanced photon source on sector 4-ID-D. Spectra were collected at room temperature on a powder sample (∼100 mg) in transmission mode through the Os L2 and L3 edges. Analysis was performed with the Athena software27.
Additional information
How to cite this article: Calder, S. et al. Enhanced spin-phonon-electronic coupling in a 5d oxide. Nat. Commun. 6:8916 doi: 10.1038/ncomms9916 (2015).
References
Khomskii, D. Transition Metal Compounds Cambridge University Press (2014).
Pesin, D. & Balents, L. Mott physics and band topology in materials with strong spin–orbit interaction. Nat. Phys. 6, 376–381 (2010).
Witczak-Krempa, W., Chen, G., Kim, Y. B. & Balents, L. Correlated quantum phenomena in the strong spin-orbit regime. Annu. Rev. Condens. Matter Phys. 5, 57–82 (2014).
Kim, B. J. et al. Phase-sensitive observation of a spin-orbital mott state in Sr2IrO4 . Science 323, 1329–1332 (2009).
Kim, J. W. et al. Dimensionality driven spin-flop transition in layered iridates. Phys. Rev. Lett. 109, 037204 (2012).
Boseggia, S. et al. Robustness of basal-plane antiferromagnetic order and the Jeff=1/2 state in single-layer iridate spin-orbit mott insulators. Phys. Rev. Lett. 110, 117207 (2013).
Slater, J. C. Magnetic effects and the Hartree-Fock equation. Phys. Rev. 82, 538–541 (1951).
Shi, Y. G. et al. Continuous metal-insulator transition of the antiferromagnetic perovskite NaOsO3 . Phys. Rev. B 80, 161104 (2009).
Calder, S. et al. Magnetically driven metal-insulator transition in NaOsO3 . Phys. Rev. Lett. 108, 257209 (2012).
Vecchio, I. L. et al. Infrared evidence of a Slater metal-insulator transition in NaOsO3 . Sci. Rep. 3, 2990 (2013).
Lee, J. H. et al. A strong ferroelectric ferromagnet created by means of spin–lattice coupling. Nature 466, 954–958 (2010).
Lee, J. H. & Rabe, K. M. Epitaxial-Strain-Induced multiferroicity in SrMnO3 from First Principles. Phys. Rev. Lett. 104, 207204 (2010).
Kim, K. W. et al. Ultrafast transient generation of spin-density-wave order in the normal state of BaFe2As2 driven by coherent lattice vibrations. Nat. Mater. 11, 497–501 (2012).
Sakai, H. et al. Displacement-type ferroelectricity with off-center magnetic ions in perovskite Sr1-xBaxMnO3 . Phys. Rev. Lett. 107, 137601 (2011).
Kamba, S. et al. Strong spin-phonon coupling in infrared and Raman spectra of SrMnO3 . Phys. Rev. B 89, 064308 (2014).
Garcia-Flores, A. F. et al. Spin-electron-phonon excitation in Re-based half-metallic double perovskites. Phys. Rev. Lett. 108, 177202 (2012).
Padilla, W. J., Mandrus, D. & Basov, D. N. Searching for the Slater transition in the pyrochlore Cd2Os2O7 with infrared spectroscopy. Phys. Rev. B 66, 035120 (2002).
Yamaura, J. et al. Tetrahedral magnetic order and the metal-insulator transition in the pyrochlore lattice of Cd2Os2O7 . Phys. Rev. Lett. 108, 247205 (2012).
Lee, J. H., Delaney, K. T., Bousquet, E., Spaldin, N. A. & Rabe, K. M. Strong coupling of Jahn-Teller distortion to oxygen-octahedron rotation and functional properties in epitaxially strained orthorhombic LaMnO3 . Phys. Rev. B 88, 174426 (2013).
Chen, G. & Balents, L. Spin-orbit coupling in d2 ordered double perovskites. Phys. Rev. B 84, 094420 (2011).
Azuah, R. T. et al. DAVE: A comprehensive software suite for the reduction, visualization, and analysis of low energy neutron spectroscopic data. J. Res. Natl Inst. Stan. Technol. 114, 341–358 (2009).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Lee, J. H. & Rabe, K. M. Large spin-phonon coupling and magnetically-induced phonon anisotropy in SrMO3 perovskites (M=V,Cr,Mn,Fe,Co). Phys. Rev. B 84, 104440 (2011).
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study. Phys. Rev. B 57, 1505–1509 (1998).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Farrow, C. L. et al. PDFfit2 and PDFgui: computer programs for studying nanostructure in crystals. J. Phys. Condens. Matter. 19, 335219 (2007).
Ravel, B. & Newville, M. ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron. Radiat. 12, 537–541 (2005).
Acknowledgements
Research conducted at ORNL's Spallation Neutron Source was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, US Department of Energy. Part of the research at ORNL was sponsored by the Scientific User Facilities Division and Materials Sciences and Engineering Division (J.H.L. and J.-Q.Y). Z.Z. was partially supported by the CEM and NSF MRSEC under Grant No. DMR-1420451. Use of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. DOE Office of Science by Argonne National Laboratory, was supported by the U.S. DOE under Contract No. DE-AC02-06CH11357. Research was supported in part by Grant-in-Aid for Scientific Research (22246083, 22850019, 25289233) from JSPS and FIRST Program from JSPS and ALCA program from JST and the Ministry of Science and Technology of China (973 Project No. 2011CBA00110). This research was supported by National Natural Science Foundation of China (No. 11274367)).
Author information
Authors and Affiliations
Contributions
S.C., M.B.S., M.D.L., A.D.C. and M.F. conceived and performed the neutron experiments. J.C.L. performed the X-ray measurement. Y.G.S., Y.S.S., Y.T., K.Y. prepared the NaOsO3 sample and J.Q.Y. and Z.Z. prepared the Cd2Os2O7 sample. J.H.L. performed the DFT calculations. S.C. and J.H.L. led the manuscript preparation with contributions from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-4, Supplementary Note 1 and Supplementary References (PDF 968 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Calder, S., Lee, J., Stone, M. et al. Enhanced spin-phonon-electronic coupling in a 5d oxide. Nat Commun 6, 8916 (2015). https://doi.org/10.1038/ncomms9916
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms9916
This article is cited by
-
Aberrant electronic and structural alterations in pressure tuned perovskite NaOsO3
npj Quantum Materials (2020)
-
Unconventional spin-phonon coupling via the Dzyaloshinskii–Moriya interaction
npj Quantum Materials (2019)
-
Two-magnon scattering in the 5d all-in-all-out pyrochlore magnet Cd2Os2O7
Nature Communications (2017)
-
Electromagnon dispersion probed by inelastic X-ray scattering in LiCrO2
Nature Communications (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.