Abstract
The switching between topologically distinct skyrmionic and ferromagnetic states has been proposed as a bit operation for information storage. While long lifetimes of the bits are required for data storage devices, the lifetimes of skyrmions have not been addressed so far. Here we show by means of atomistic Monte Carlo simulations that the field-dependent mean lifetimes of the skyrmionic and ferromagnetic states have a high asymmetry with respect to the critical magnetic field, at which these lifetimes are identical. According to our calculations, the main reason for the enhanced stability of skyrmions is a different field dependence of skyrmionic and ferromagnetic activation energies and a lower attempt frequency of skyrmions rather than the height of energy barriers. We use this knowledge to propose a procedure for the determination of effective material parameters and the quantification of the Monte Carlo timescale from the comparison of theoretical and experimental data.
Similar content being viewed by others
Introduction
Magnetic skyrmions1 are vortex-like spin structures that have been observed at the nanometre scale in bulk non-centrosymmetric crystals2,3,4,5, in thin films of cubic helimagnets6,7,8 and in ultrathin films at surfaces9,10. Typically, skyrmions are formed due to the competition of the exchange and the Dzyaloshinskii–Moriya (DM) interactions11,12 in the presence of a magnetic field. Skyrmions exhibit particle-like properties and can emerge as isolated objects or in a close-packed lattice. The three-dimensional spins forming a skyrmion point in all directions wrapping a sphere, which gives rise to its topological stability against deformation into the ferromagnetic (FM) phase.
This robustness in combination with a small lateral size in the nanometre range has led to propositions to use skyrmions as bits of information in future data storage devices13,14. The realization of such a device requires the possibility to deliberately create and annihilate individual skyrmions as well as to manipulate their spatial position. There are several experimental and theoretical studies dealing with the motion of skyrmions driven by currents and temperature gradients15,16,17,18,19,20,21,22,23,24,25,26,27. In the continuum model, transitions between skyrmionic (Sk) and FM states are forbidden because of the topological protection. It is, however, commonly believed that in a real magnetic system with discrete atomic magnetic moments, the topological protection accounts for an energy barrier separating the two distinct states. This interpretation is justified by the fact that transitions between the Sk and FM states may be induced by a variation of the magnetic field and a coupling of the system to an external bath as has been shown both theoretically and experimentally in various studies2,6,10,16,28,29,30,31,32,33. In particular, the unwinding of skyrmion tubes into the helical spin state has been investigated with Monte Carlo (MC) simulations30 and the stochastic Landau-Lifshitz-Gilbert equation33 for chiral magnets. The main finding was that the annihilation process of these skyrmion tubes is governed by the dynamics of the formation of emergent magnetic monopoles and antimonopoles. Furthermore, the switching of skyrmions induced by local heating within a FM ultrathin magnetic film was studied with the stochastic Landau-Lifshitz-Gilbert equation as a function of heating time, intensity and area, recently32.
However, the shape of the energy landscape between the FM and Sk states and its impact on the transition dynamics are still unknown. The knowledge about the energy landscape of Sk systems is of huge importance for tailoring these nontrivial magnetic structures according to the requirements of data storage devices. While there are numerous MC studies30,34,35,36 dealing with the phase diagram, here we report on MC simulations regarding the kinetic properties of Sk and FM states in ultrathin magnetic films as a function of temperature and magnetic field. In our investigations, we find that the energy landscape of a Sk system is very different from that of magnetic atomic clusters and nanoislands exhibiting two-state behaviour with degenerate energy minima, which are symmetric with respect to the energy barrier37,38. The validity of the numerical results are tested by experimental data obtained on a Pd/Fe bilayer on an Ir(111) substrate. This allows us to propose a procedure for the determination of effective material parameters of real systems from quantification of MC mean lifetimes and magnetic fields using experimental data as shown exemplarily for a Pd/Fe bilayer on Ir(111).
Results
Monte Carlo analysis
For the sake of generality, we describe an ultrathin magnetic film by the standard effective Hamiltonian

within the Heisenberg model. Therein, Si=μi/μ is a three-dimensional magnetic moment of unit length, K describes the uniaxial perpendicular magnetic anisotropy and B is the uniform external magnetic field. J is the effective nearest-neighbour exchange integral and Di,j is an effective DM coupling. The DM interaction arises, for example, due to the coupling of two atomic spins in a magnetic surface layer to a third atom of the supporting crystal, which exhibits a large spin–orbit coupling39. For symmetry reasons, we chose the DM vector Di,j to be perpendicular to the vector connecting two spins Si and Sj and to lie within the plane of the magnetic film40.
Systems consisting of up to 1,000 Heisenberg spins on a two-dimensional triangular lattice with a hexagonal boundary shape (Fig. 1a) using helical boundary conditions41 have been investigated by means of extended MC simulations (see the Methods section). Energy parameters typical for thin films showing Sk phases, that is, D/J≈0.3 and K≈0.1 J have been used42,43.
(a) Triangular spin lattice with a hexagonal boundary shape containing a single skyrmion at kBT=0.05 J and μB=0.1 J. (b) The inset displays the DM energy as a function of the Monte Carlo step (MCS) for different magnetic field strengths at kBT=0.61 J exhibiting a two-state behaviour due to the ongoing creation and annihilation of a single skyrmion. The size of the system is such that it contains a maximum of one skyrmion at a given MCS. The histogram of the DM energy shows two peaks corresponding to the FM and Sk states. The Sk and FM states are populated with equal probability at the critical field Bc and the areas underneath the peaks of the histogram are equal.
A thin magnetic film, which can be described by the equation (1), exhibits a rich phase space6. At low temperatures, the system exhibits a spin-spiral state in zero field and forms a temperature-dependent skyrmion lattice (Skx) or a skyrmion gas (Skg) in a perpendicular field. In a sufficiently large field, the system becomes fully polarized and transforms into a FM state. The simulations have been performed at fields and temperatures near the phase boundary separating the FM and Sk phases where individual skyrmions are formed. In this region of the phase space, the distance between skyrmions is much larger than the skyrmion diameter and the energies of the Sk and the FM states are nearly degenerate. Therefore, a thermally activated creation and annihilation of single skyrmions within the FM phase is expected. The size of the investigated system was adapted in such a way that only one single skyrmion was stochastically created and annihilated within the system near the critical field Bc separating the FM and Sk phases as a function of the time measured in MC steps (MCSs; see the Methods section). This switching behaviour was characterized by the calculation of the time dependence of the winding number oscillating between zero and unity and the DM energy exhibiting abrupt changes when a skyrmion is created or annihilated. As the DM energy is less dependent on local inhomogeneities of magnetic structures at high temperatures, we use it to plot and evaluate the telegraph noise due to the ongoing creation and annihilation of a skyrmion.
Mean lifetimes
Figure 1b shows the histograms of the DM energies, which exhibit two peaks corresponding to the FM and Sk states. The peaks of the Sk states are much broader than those of the FM, which is due to thermally induced fluctuations in the skyrmion size. In addition, the peak of the Sk state shifts to higher energies with an increasing field indicating that the skyrmion equilibrium size decreases with the field44. As the probability to find the system in either state is equivalent to the area underneath the peaks, the areas are equal for both states at Bc only. The mean lifetimes  and
and  cannot be deduced directly from the histograms but are rather determined as
cannot be deduced directly from the histograms but are rather determined as  from the individual lifetimes τSk,i and τFM,i shown in the inset of Fig. 1b. For this purpose, more than N=1,000 switching events have been recorded for each set of temperature and field to achieve reliable statistics. The inset in Fig. 1b shows the DM energy as a function of the MC time at three different magnetic fields for the temperature kBT=0.61 J. While the system is found with equal probabilities in the Sk and FM states at the critical field of μBc=0.103 J, the Sk state becomes preferred for fields B<Bc as shown for μB1=0.093 J. This population imbalance gets inverted in the range B>Bc at which the FM state becomes more stable as shown for μB2=0.114 J.
from the individual lifetimes τSk,i and τFM,i shown in the inset of Fig. 1b. For this purpose, more than N=1,000 switching events have been recorded for each set of temperature and field to achieve reliable statistics. The inset in Fig. 1b shows the DM energy as a function of the MC time at three different magnetic fields for the temperature kBT=0.61 J. While the system is found with equal probabilities in the Sk and FM states at the critical field of μBc=0.103 J, the Sk state becomes preferred for fields B<Bc as shown for μB1=0.093 J. This population imbalance gets inverted in the range B>Bc at which the FM state becomes more stable as shown for μB2=0.114 J.
Figure 2a shows the effect of both the magnetic field and the temperature on the mean lifetimes within the range μB=(0.093–0.114) J and kBT=(0.6–0.7)J. The red points give  and the black points
and the black points  as determined from the MC calculations. For a fixed temperature, the Sk state gets destabilized by an increasing field and, therefore, the mean lifetime of a skyrmion decreases. The FM state, in contrast, gets stabilized and the corresponding mean lifetime increases. Surprisingly, the mean lifetimes exhibit a very asymmetric behaviour with respect to the intersection point
as determined from the MC calculations. For a fixed temperature, the Sk state gets destabilized by an increasing field and, therefore, the mean lifetime of a skyrmion decreases. The FM state, in contrast, gets stabilized and the corresponding mean lifetime increases. Surprisingly, the mean lifetimes exhibit a very asymmetric behaviour with respect to the intersection point  showing that the Sk and FM states respond differently to changes in the magnetic field. Such an asymmetry can appear for several reasons including field dependent changes in the activation energy, in the energies of the Sk and FM states or in the dynamics.
showing that the Sk and FM states respond differently to changes in the magnetic field. Such an asymmetry can appear for several reasons including field dependent changes in the activation energy, in the energies of the Sk and FM states or in the dynamics.
(a)Mean lifetimes of the Sk and FM states as a function of the magnetic field and the temperature. The red and black points are the results of MC calculations. The points of intersection  are marked by green spheres. A cross-section of the data is shown in Fig. 3a with the same colour coding. The inset of a shows a sketch of the energy landscape. The energy minima ESk and EFM of the Sk and FM states are separated by activation energies given by
are marked by green spheres. A cross-section of the data is shown in Fig. 3a with the same colour coding. The inset of a shows a sketch of the energy landscape. The energy minima ESk and EFM of the Sk and FM states are separated by activation energies given by  and
and  , respectively. (b) The energies ESk and EFM of the Sk and FM states, respectively, as a function of the magnetic field for the temperature kBT=0.61 J alongside with the energy of the energy barrier EB, which is given by the sum of the energy levels and activation energies. (c) The attempt frequencies ν0.
, respectively. (b) The energies ESk and EFM of the Sk and FM states, respectively, as a function of the magnetic field for the temperature kBT=0.61 J alongside with the energy of the energy barrier EB, which is given by the sum of the energy levels and activation energies. (c) The attempt frequencies ν0.
Energy landscape
To clarify the asymmetric behaviour of the mean lifetimes, particular attention has to be paid to the shape of the energy landscape and its dependence on the magnetic field in the vicinity of Bc. As a starting point, we consider a simplified one-dimensional energy landscape (Fig. 2a, inset) with two energy minima ESk and EFM of the Sk and FM states, which are separated by an energy barrier giving rise to the two activation energies  and
and  , respectively. The reaction coordinate γ describes the spin configurations between the two energy minima. The field dependences of EFM and ESk can immediately be derived from the MC calculations. Figure 2b shows ESk with respect to EFM at the temperature kBT=0.61 J. Both energies decrease linearly with the field, which is evident for the FM because of its direct Zeeman proportionality but is less trivial for the Sk state. The total energy of a single skyrmion may show some nonlinearity when examining large field ranges45, however, for a limited field range around Bc, we find a linear dependence of its energy on the applied field. The FM state is energetically favoured over the Sk state over the full range of investigated fields. A linear extrapolation of EFM and ESk to smaller fields yields a degeneracy at μB=0.065 J. Note that the skyrmion is more stable
, respectively. The reaction coordinate γ describes the spin configurations between the two energy minima. The field dependences of EFM and ESk can immediately be derived from the MC calculations. Figure 2b shows ESk with respect to EFM at the temperature kBT=0.61 J. Both energies decrease linearly with the field, which is evident for the FM because of its direct Zeeman proportionality but is less trivial for the Sk state. The total energy of a single skyrmion may show some nonlinearity when examining large field ranges45, however, for a limited field range around Bc, we find a linear dependence of its energy on the applied field. The FM state is energetically favoured over the Sk state over the full range of investigated fields. A linear extrapolation of EFM and ESk to smaller fields yields a degeneracy at μB=0.065 J. Note that the skyrmion is more stable  for μB<0.103 J.
for μB<0.103 J.
The energy of the separating barrier is more difficult to access because the intermediate spin configurations are yet unknown. However,  and
and  can be derived from the temperature dependence of the mean lifetimes, which are found to decrease exponentially with the temperature allowing to describe them with the Arrhenius law by the functions
can be derived from the temperature dependence of the mean lifetimes, which are found to decrease exponentially with the temperature allowing to describe them with the Arrhenius law by the functions


with the attempt frequencies  and
and  . The activation energies derived from fits of numerical data by equations (2) and (3) correspond to the vertical heights of the shaded areas in Fig. 2b.
. The activation energies derived from fits of numerical data by equations (2) and (3) correspond to the vertical heights of the shaded areas in Fig. 2b.  and
and  both depend linearly on the magnetic field.
both depend linearly on the magnetic field.  decreases from 7.4 to 4.7 J in the investigated field range, while
decreases from 7.4 to 4.7 J in the investigated field range, while  increases only slightly and is about 11 J. The observation that
increases only slightly and is about 11 J. The observation that  responds more sensitive to changes in the field than
responds more sensitive to changes in the field than  may be explained by the fact that the magnetic microstructure of the FM state remains unchanged (up to fluctuations) with increasing field strength, while the size of an isolated skyrmion shows a field dependence44,45. A similar activated behaviour as described by equation (3) with a comparable value for
may be explained by the fact that the magnetic microstructure of the FM state remains unchanged (up to fluctuations) with increasing field strength, while the size of an isolated skyrmion shows a field dependence44,45. A similar activated behaviour as described by equation (3) with a comparable value for  was found for bulk Sk systems33.
was found for bulk Sk systems33.
The energy of the barrier state EB is given by the sums of the energies of the FM and Sk states and the corresponding activation energies as  and
and  . The energies
. The energies  and
and  , shown by the black and red triangles in Fig. 2b, coincide within the range of numerical accuracy indicating that the system passes the same barrier state for both transition directions justifying the one-dimensional picture of the energy landscape.
, shown by the black and red triangles in Fig. 2b, coincide within the range of numerical accuracy indicating that the system passes the same barrier state for both transition directions justifying the one-dimensional picture of the energy landscape.
Summing up, we have found that for fields B<Bc the Sk state is more stable than its FM counterpart despite the fact that it is still energetically less favourable. Also, the activation energy of the Sk is smaller than that of the FM in this range. Thus, the intrinsic energy and the activation energy cannot be the dominating mechanism stabilizing the skyrmion. To shed light onto this finding, the attempt frequencies have been investigated. From the Arrhenius fit we find that the attempt frequencies are on the order of  and
and  throughout the whole range of explored magnetic fields (Fig. 2c). We identify the large difference in the attempt frequencies as the reason for the stability of the Sk state for fields B<Bc in the present MC calculations.
throughout the whole range of explored magnetic fields (Fig. 2c). We identify the large difference in the attempt frequencies as the reason for the stability of the Sk state for fields B<Bc in the present MC calculations.
To find a physical reason for the large difference of the attempt frequencies, the entropy of the system with and without a skyrmion46 has been estimated as presented in Supplementary Note 1 and Supplementary Fig. 1. The entropy difference is found to be of the order of 0.7–0.9 meV K−1. According to our analysis, the ratio of the attempt frequencies can be identified with this entropy difference47. Due to the higher entropy of the Sk state, the critical field Bc(T) increases with the temperature (Supplementary Fig. 2). These data also imply that the energy minimum of the Sk state is broader than that of the FM state since the attempt frequencies describe in the first approximation the geometry of the energy landscape in the vicinity of the energy minima using Kramers’ description of the escape rate in the regime of high damping48 (Supplementary Note 2).
Deducing energy parameters
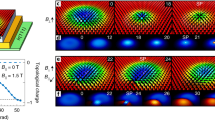
The calculations presented above concern a generic two-dimensional Sk system, which can effectively be described by an Hamiltonian of equation (1). In the following, we compare our numerical findings with experimental results obtained for Pd/Fe/Ir(111)10. The experimental investigations on Pd/Fe/Ir(111) were performed at a temperature of 4.2 K with a spin-polarized scanning tunnelling microscope (SP-STM) using a Cr bulk tip. The system exhibits a spin-spiral state at zero magnetic field at low temperatures. In a perpendicular magnetic field, the system adapts a two-level behaviour: only Sk and FM configurations remain stable10. The temperature is such that the thermal energy alone is insufficient to go from the FM to the Sk state at moderate field values between 2.5 T and 4.5 T. Instead, the additional energy from the spin-polarized tunnel current is needed to overcome the energy barrier and to reach the other energy minimum. Single skyrmions that are pinned to atomic defects in the FM phase were observed at fields of 3.5–4 T. Within this field range, using a spin-polarized tunnel current I=100 nA and an applied voltage of U=±600 mV, a stochastic switching between the Sk and the FM states was induced and the corresponding telegraph signal in the differential conductance has been recorded10.
To justify a comparison between these experimental data and the present MC calculations, particular attention has to be paid to the origin of the excitations leading to the spontaneous switching between the two states. In standard MC simulations, the system under investigation is in equilibrium with a thermal bath, which is described by the energy Eb being an essential part of the Boltzmann probability  . The exact origin of Eb is never addressed and is traditionally attributed to the thermal energy Eb=kBT. In the present experimental system, the spontaneous switching between the two states is not purely induced by thermal energy. Instead, the dominant mechanism was found to be the injection of additional energy due to tunnelling electrons from the tip of a spin-polarized scanning tunnelling microscopy10. Here we assume that the MC temperature includes both thermal and electronic excitations. Note also that the experiments were performed on skyrmions located at local atomic defects, which were neglected within the MC simulations.
. The exact origin of Eb is never addressed and is traditionally attributed to the thermal energy Eb=kBT. In the present experimental system, the spontaneous switching between the two states is not purely induced by thermal energy. Instead, the dominant mechanism was found to be the injection of additional energy due to tunnelling electrons from the tip of a spin-polarized scanning tunnelling microscopy10. Here we assume that the MC temperature includes both thermal and electronic excitations. Note also that the experiments were performed on skyrmions located at local atomic defects, which were neglected within the MC simulations.
Figure 3a shows experimentally obtained mean lifetimes of the Sk and FM states as a function of B for the bias voltage of U=−600 mV. The functions show a very good qualitative agreement with the theoretically obtained data of Fig. 2a. In agreement with the MC data, the lifetimes are strongly asymmetric with respect to the critical field Bc≈3.9 T at which the lifetimes are equal. This finding allows us to compare the experimental and MC mean lifetimes. More than that, we propose to calibrate our MC results using the experimental data by linearly rescaling  in such a way that the MC intersection point
in such a way that the MC intersection point  coincides with that found experimentally. Now, the task remains to determine the correct MC temperature at which the field-dependent mean lifetimes best fit to the experimental data. To find the required MC temperature,
coincides with that found experimentally. Now, the task remains to determine the correct MC temperature at which the field-dependent mean lifetimes best fit to the experimental data. To find the required MC temperature,  was described by exponential functions of the form
was described by exponential functions of the form
(a) The mean lifetimes obtained from experiments on Pd/Fe/Ir(111) as a function of the magnetic field B in combination with mean lifetimes obtained from MC calculations. The MC data are linearly rescaled to the experimental data such that the critical points given by  coincide. The lifetimes are described by exponential functions
coincide. The lifetimes are described by exponential functions  . (b) λFM/Sk for the experimental data (exp) and MC data (MC). The values
. (b) λFM/Sk for the experimental data (exp) and MC data (MC). The values  depend on the MC temperature used. The best correspondence between experiment and MC is found using the MC temperature kBT≈0.48 J marked by the vertical grey line. The calibration of the MC mean lifetimes at this temperature with the experimental lifetimes provide an absolute value for the exchange parameter of J=7.1±0.2 meV. (c) The skyrmion probability
depend on the MC temperature used. The best correspondence between experiment and MC is found using the MC temperature kBT≈0.48 J marked by the vertical grey line. The calibration of the MC mean lifetimes at this temperature with the experimental lifetimes provide an absolute value for the exchange parameter of J=7.1±0.2 meV. (c) The skyrmion probability  .
.

with the fit parameters λFM/Sk as proposed in ref. 33 for the Sk state. The horizontal black and red lines in Fig. 3b show the values  and
and  obtained from fits to the experimental data. The thickness of these lines gives the uncertainty. For the MC data, the values
obtained from fits to the experimental data. The thickness of these lines gives the uncertainty. For the MC data, the values  depend on the MC temperature and are shown by the red and black dashed lines in Fig. 3b. The curves
depend on the MC temperature and are shown by the red and black dashed lines in Fig. 3b. The curves  and
and  intersect at kBT=0.48 J, while no intersection can be observed for
intersect at kBT=0.48 J, while no intersection can be observed for  and
and  within the explored MC temperature range. We conclude that the best agreement between experiment and MC simulations is obtained for the MC temperature kBT≈0.48 J. Note that for kBT<0.58 J, the MC mean lifetimes were extrapolated from the temperature-dependent calculations because of insufficient MC statistics in direct simulations. The feasibility of the proposed calibration method has been confirmed by the calculation of the Sk probability
within the explored MC temperature range. We conclude that the best agreement between experiment and MC simulations is obtained for the MC temperature kBT≈0.48 J. Note that for kBT<0.58 J, the MC mean lifetimes were extrapolated from the temperature-dependent calculations because of insufficient MC statistics in direct simulations. The feasibility of the proposed calibration method has been confirmed by the calculation of the Sk probability  (Fig. 3c), which is 0.5 at the critical field Bc and approaches 1 for small and 0 for large fields. The experimentally and numerically determined curves show a good agreement.
(Fig. 3c), which is 0.5 at the critical field Bc and approaches 1 for small and 0 for large fields. The experimentally and numerically determined curves show a good agreement.
From the correspondence between the experimental and the MC time at Bc, the physical timescale is immediately set such that 1 MCS corresponds to 2 × 10−9 s. From the knowledge of the experimental Bc, the MC field is derived by the scaling factor  . Taking the magnetic moment μ=3 μB for Pd/Fe/Ir(111)42 into account, all coupling constants can naturally be determined. According to the described calculations the nearest-neighbour effective exchange interaction for Pd/Fe/Ir(111) equals J=7±0.2 meV per bond, while the DM parameter is D=2.2 meV per bond. Our value for D is in a good agreement with those given in refs 42, 43, 49, while our value for the effective nearest-neighbour interaction is somewhat smaller compared with the values for the nearest-neighbour interaction in refs 42, 43. This difference in J may be explained by the fact that compensating antiferromagnetic interactions between more distant neighbours42,43 are mapped onto our effective nearest-neighbour exchange parameter. From the above considerations, the activation energies between single skyrmions and the FM phase in Pd/Fe/Ir(111) are on the order of
. Taking the magnetic moment μ=3 μB for Pd/Fe/Ir(111)42 into account, all coupling constants can naturally be determined. According to the described calculations the nearest-neighbour effective exchange interaction for Pd/Fe/Ir(111) equals J=7±0.2 meV per bond, while the DM parameter is D=2.2 meV per bond. Our value for D is in a good agreement with those given in refs 42, 43, 49, while our value for the effective nearest-neighbour interaction is somewhat smaller compared with the values for the nearest-neighbour interaction in refs 42, 43. This difference in J may be explained by the fact that compensating antiferromagnetic interactions between more distant neighbours42,43 are mapped onto our effective nearest-neighbour exchange parameter. From the above considerations, the activation energies between single skyrmions and the FM phase in Pd/Fe/Ir(111) are on the order of  and
and  at the temperature kBT=0.48 J. This is somewhat smaller than activation barriers observed for nanoscale Fe/W islands of comparable size50 (≈100 atoms) to the skyrmions.
at the temperature kBT=0.48 J. This is somewhat smaller than activation barriers observed for nanoscale Fe/W islands of comparable size50 (≈100 atoms) to the skyrmions.
Discussion
The overall good agreement suggests that the present MC simulations are suited to describe Sk systems and capture the physics of the creation and annihilation of individual skyrmions. The results of our general MC treatment reveal several important peculiarities of the switching between single Sk and FM states. The most important finding is that in contrast to other nanomagnets the field-dependent mean lifetimes of the Sk and FM states are strongly asymmetric. Our analysis reveals that the stability of skyrmions is hidden in the dynamics and the geometry of the energy landscape. Particularly, the attempt frequency of the skyrmion annihilation is orders of magnitudes smaller than that of the skyrmion creation due to a more shallow shape of the potential. The good agreement of these general conclusions with the experimental data on the Pd/Fe bilayer on Ir(111) allow us to make predictions about the applicability of field stabilized skyrmions in thin magnetic films for data storage devices. First, to be able to populate the two states corresponding to 0 and 1 with an equal probability the applied magnetic field has to be close to Bc. Second, to ensure the stability of the two states of a bit, the energy barrier and hence the activation energy has to be optimized. For the particular example of Pd/Fe Ir(111), we find that the upper limit for  year at Bc corresponds to a temperature of T=19 K (Supplementary Note 3; Supplementary Fig. 3). Thus, a device on the basis of this material will be able to operate at the temperature of liquid He only. To increase the operation temperature, the activation energies need to be larger while leaving the D/J ratio constant. We speculate that this can be achieved by a coherent increase of both energy parameters by, for example, using multilayers to increase the number of nearest-neighbours and at the same time the number of interfaces, which are necessary for a strong DM coupling. With a Jeff=100 meV per bond one gets stable skyrmions at 300 K. We anticipate that our studies will help to systematically tailor magnetic Sk systems for future information storage applications.
year at Bc corresponds to a temperature of T=19 K (Supplementary Note 3; Supplementary Fig. 3). Thus, a device on the basis of this material will be able to operate at the temperature of liquid He only. To increase the operation temperature, the activation energies need to be larger while leaving the D/J ratio constant. We speculate that this can be achieved by a coherent increase of both energy parameters by, for example, using multilayers to increase the number of nearest-neighbours and at the same time the number of interfaces, which are necessary for a strong DM coupling. With a Jeff=100 meV per bond one gets stable skyrmions at 300 K. We anticipate that our studies will help to systematically tailor magnetic Sk systems for future information storage applications.
Methods
Simulation details
All Monte Carlo calculations presented in the main text were performed with the Metropolis algorithm on a two-dimensional triangular lattice of N=631 sites with a hexagonal boundary shape. Each MC step consisted of N trial manipulations. The choice of the system size was made such to best meet the requirements of the problem at hand and is discussed within the section Choice of system size below. Each site was populated by a classical Heisenberg moment  of unit length Si=μi/μ. Helical boundary conditions were used in order to minimize finite size effects.
of unit length Si=μi/μ. Helical boundary conditions were used in order to minimize finite size effects.
We considered a Hamilton operator of the form

including the exchange interaction, DM interaction, Zeeman energy and anisotropy energy. The exact terms of these energies are given in the main text. For all simulations presented in the main text, system parameters D and J with a ratio of D/J=0.32 and an easy perpendicular anisotropy axis of K=0.07 J were used. We confirmed that this system shows a phase space behaviour qualitatively similar to the observations made in ref. 6.
In zero field at kBT=0.06 J, the system exhibits spin-spirals with a period of λ≈5 nm (Fig. 4) assuming the lattice constant a=2.7 Å of Fe/Ir(111)9. This value for the spin-spiral period is somewhat smaller than the ones found experimentally for Pd/Fe/Ir(111), which are on the order of 6–7 nm (ref. 10). To determine the spin-spiral period, we chose a system of ∼3 × 104 Heisenberg spins on a triangular lattice with open boundary conditions to achieve a sufficient number of spin spirals. The temperature was successively decreased from kBT=0.61 J for an arbitrary initial spin configuration to kBT=0.06 J using 40 temperature steps with 105 MCS each. Note that the boundary shape of the lattice used for these MC simulations was adapted to resemble the typical island shapes found in the experimental investigations of Pd/Fe/Ir(111)10.
Density plot of spin-spirals obtained with MC simulations in zero field at a temperature of kBT=0.06 J. The spin-spiral period is determined to be λ≈5 nm considering the lattice constant a=2.7 Å of Fe/Ir(111)9.
The focus of the investigations in the main text was laid upon the field region in which the Sk and FM states become energetically nearly degenerate and thus allow for a thermally activated spontaneous creation and annihilation of individual skyrmions in the FM phase as a function of the time given in MCS. This switching behaviour was characterized by the winding number and the DM energy shown exemplarily in Fig. 5 for kBT=0.61 J and μB=0.1 J and the system size N=631. The DM energy exhibits a two-level behaviour while the winding number adopts discrete natural number values between zero and two for these parameters within this range of MCS. The winding number switches predominantly between zero and one corresponding to the two levels in the DM energy. However, local fluctuations add or remove a skyrmion to the winding number which we neglect when counting the total number of skyrmions within the system. Hence, we use for convenience the DM energy to investigate the switching behaviour and to determine the mean lifetimes since the DM energy is less sensitive to local fluctuations.
In the following, we comment on the method by which the switching events between the Sk and FM states were identified. The frequency distribution of the DM energy at a particular temperature and magnetic field exhibits two peaks corresponding to the FM and Sk states as discussed in the main text and shown in Fig. 6 for kBT=0.61 J, μB=0.1 J and a system size N=631. The peak positions are located at the mean DM energies  and
and  of the FM and Sk states as shown by the horizontal grey and black lines. The switching events are identified by finding the coincidences at which the DM energy subsequently crosses the energies
of the FM and Sk states as shown by the horizontal grey and black lines. The switching events are identified by finding the coincidences at which the DM energy subsequently crosses the energies  and
and  in either direction. In Fig. 6, a switching event from the FM to the Sk state is shown.
in either direction. In Fig. 6, a switching event from the FM to the Sk state is shown.
DM energy as a function of the time given in MC steps for kBT=0.61 J, μB=0.1 J and a system size N=631 exhibiting a two-state behaviour due to the ongoing creation and annihilation of a single skyrmion. The frequency distribution of the DM energies exhibits two peaks whose positions  and
and  are marked by the grey and black horizontal lines. A switching event is identified by the coincidence when the DM energy subsequently crosses these two energies from either direction.
are marked by the grey and black horizontal lines. A switching event is identified by the coincidence when the DM energy subsequently crosses these two energies from either direction.
Choice of system size
The total number of skyrmions that can be present in the system simultaneously depends on the system size N. Therefore, the system size has an influence on the stability of an individual skyrmion. Figure 7 shows the mean lifetimes of the FM state and an individual skyrmion as a function of the system size for kBT=0.61 J and μB=0.1 J. We restricted the system to geometries with a hexagonal boundary shape leaving only discrete possible values for N. The red and black points mark the mean lifetimes for the values of N that comply with this constriction. The system can contain a maximum of one skyrmion for relatively small system sizes N<800. In the range 500<N<800, the single skyrmion is the more probable state compared to the ferromagnet. For system sizes N<500, this stability relation is inverted and the ferromagnet is the more probable state. This behaviour may be ascribed to two effects. First, the skyrmion is restricted to a smaller region with a reduction of the system size providing less space to evade local perturbations. Second, the system eventually becomes too small to allow the formation of a whole skyrmion. In systems larger than N≈800, multiple skyrmions may be present within the system at the same time. Since we wanted to investigate the stability properties of an individual skyrmion, we chose a system size of N=631 marked by the grey vertical line, which is close to the region allowing for multiple skyrmions.
The mean lifetimes  as a function of the system size N for kBT=0.61 J and μB=0.1 J. Since triangular lattices with a hexagonal boundary shape are considered, discrete values of N are possible only. The red and black points mark the mean lifetimes for the values of N that comply with this constriction. The shaded area to the right side marks the region in which the system size is large enough to allow two skyrmions to be present simultaneously. We chose the system size N=631, which is marked by the grey vertical line for the simulations presented in the main text.
as a function of the system size N for kBT=0.61 J and μB=0.1 J. Since triangular lattices with a hexagonal boundary shape are considered, discrete values of N are possible only. The red and black points mark the mean lifetimes for the values of N that comply with this constriction. The shaded area to the right side marks the region in which the system size is large enough to allow two skyrmions to be present simultaneously. We chose the system size N=631, which is marked by the grey vertical line for the simulations presented in the main text.
Additional information
How to cite this article: Hagemeister, J. et al. Stability of single skyrmionic bits. Nat. Commun. 6:8455 doi: 10.1038/ncomms9455 (2015).
References
Rößler, U. K., Bogdanov, A. N. & Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 442, 797–801 (2006).
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Pappas, C. et al. Chiral paramagnetic skyrmion-like phase in MnSi. Phys. Rev. Lett. 102, 197202 (2009).
Tonomura, A. et al. Real-space observation of skyrmion lattice in helimagnet MnSi thin samples. Nano Lett. 12, 1673–1677 (2012).
Moskvin, E. et al. Complex chiral modulations in FeGe close to magnetic ordering. Phys. Rev. Lett. 110, 077207 (2013).
Yu, X. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Yu, X. Z. et al. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 10, 106–109 (2011).
Seki, S., Yu, X. Z., Ishiwata, S. & Tokura, Y. Observation of skyrmions in a multiferroic material. Science 336, 198–201 (2012).
Heinze, S. et al. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 7, 713–718 (2011).
Romming, N. et al. Writing and deleting single magnetic skyrmions. Science 341, 636–639 (2013).
Dzyaloshinskii, I. A thermodynamic theory of `weak' ferromagnetism of antiferromagnets. J. Phys. Chem. Solids 4, 241–255 (1958).
Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 120, 91–98 (1960).
Kiselev, N. S., Bogdanov, A., Schäfer, R. & Rößler, U. K. Chiral skyrmions in thin magnetic films: new objects for magnetic storage technologies? J. Phys. D Appl. Phys. 44, 392001 (2011).
Fert, A., Cros, V. & Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 8, 152–156 (2013).
Zang, J., Mostovoy, M., Han, J. H. & Nagaosa, N. Dynamics of skyrmion crystals in metallic thin films. Phys. Rev. Lett. 107, 136804 (2011).
Sampaio, J., Cros, V., Rohart, S., Thiaville, A. & Fert, A. Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nat. Nanotechnol. 8, 839–844 (2013).
Iwasaki, J., Mochizuki, M. & Nagaosa, N. Current-induced skyrmion dynamics in constricted geometries. Nat. Nanotechnol. 8, 742–747 (2013).
Iwasaki, J., Mochizuki, M. & Nagaosa, N. Universal current-velocity relation of skyrmion motion in chiral magnets. Nat. Commun. 4, 1463 (2013).
Troncoso, R. E. & Núñez, A. S. Thermally assisted current-driven skyrmion motion. Phys. Rev. B 89, 224403 (2014).
Iwasaki, J., Koshibae, W. & Nagaosa, N. Colossal spin transfer torque effect on skyrmion along the edge. Nano Lett. 14, 4432–4437 (2014).
Schütte, C., Iwasaki, J., Rosch, A. & Nagaosa, N. Inertia, diffusion and dynamics of a driven skyrmion. Phys. Rev. B 90, 174434 (2014).
Kong, L. & Zang, J. Dynamics of an insulating skyrmion under a temperature gradient. Phys. Rev. Lett. 111, 067203 (2013).
Kovalev, A. A. Skyrmionic spin Seebeck effect via dissipative thermomagnonic torques. Phys. Rev. B 89, 241101 (2014).
Lin, S.-Z., Batista, C. D., Reichhardt, C. & Saxena, A. ac current generation in chiral magnetic insulators and skyrmion motion induced by the spin Seebeck effect. Phys. Rev. Lett. 112, 187203 (2014).
Jonietz, F. et al. Spin transfer torques in MnSi at ultralow current densities. Science 330, 1648–1651 (2010).
Knoester, M. E., Sinova, J. & Duine, R. A. Phenomenology of current-skyrmion interactions in thin films with perpendicular magnetic anisotropy. Phys. Rev. B 89, 064425 (2014).
Yu, X. Z. et al. Skyrmion flow near room temperature in an ultralow current density. Nat. Commun. 3, 988 (2012).
Ezawa, M. Skyrmion burst and multiple quantum walk in thin ferromagnetic films. Phys. Lett. A 375, 3610–3614 (2011).
Tchoe, Y. & Han, J. H. Skyrmion generation by current. Phys. Rev. B 85, 174416 (2012).
Milde, P. et al. Unwinding of a skyrmion lattice by magnetic monopoles. Science 340, 1076–1080 (2013).
Lin, S.-Z., Reichhardt, C. & Saxena, A. Manipulation of skyrmions in nanodisks with a current pulse and skyrmion rectifier. Appl. Phys. Lett. 102, 222405 (2013).
Koshibae, W. & Nagaosa, N. Creation of skyrmions and antiskyrmions by local heating. Nat. Commun. 5, 5148 (2014).
Schütte, C. & Rosch, A. Dynamics and energetics of emergent magnetic monopoles in chiral magnets. Phys. Rev. B 90, 174432 (2014).
Yi, S. D., Onoda, S., Nagaosa, N. & Han, J. H. Skyrmions and anomalous Hall effect in a Dzyaloshinskii-Moriya spiral magnet. Phys. Rev. B 80, 2009 (2009).
Li, Y.-Q., Liu, Y.-H. & Zhou, Y. General spin-order theory via gauge Landau-Lifshitz equation. Phys. Rev. B 84, 205123 (2011).
Buhrandt, S. & Fritz, L. Skyrmion lattice phase in three-dimensional chiral magnets from Monte Carlo simulations. Phys. Rev. B 88, 195137 (2013).
Khajetoorians, A. A. et al. Current-driven spin dynamics of artificially constructed quantum magnets. Science 339, 55–59 (2013).
Krause, S., Berbil-Bautista, L., Herzog, G., Bode, M. & Wiesendanger, R. Current-induced magnetization switching with a spin-polarized scanning tunneling microscope. Science 317, 1537–1540 (2007).
Fert, A. Magnetic and transport properties of metallic multilayers. Mater. Sci. Forum 59-60, 439–480 (1990).
Crépieux, A. & Lacroix, C. Dzyaloshinsky-Moriya interactions induced by symmetry breaking at a surface. J. Magn. Magn. Mater. 182, 341–349 (1998).
Newman, M. E. J. & Barkema, G. T. Monte Carlo Methods in Statistical Physics Oxford Univ. Press (1999).
Dupé, B., Hoffmann, M., Paillard, C. & Heinze, S. Tailoring magnetic skyrmions in ultra-thin transition metal films. Nat. Commun. 5, 4030 (2014).
Simon, E., Palotás,, Rózsa, L., Udvardi, L. & Szunyogh, Formation of magnetic skyrmions with tunable properties in PdFe bilayer deposited on Ir(111). Phys. Rev. B 90, 094410 (2014).
Bogdanov, A. & Hubert, A. The properties of isolated magnetic vortices. Phys. Status Solidi B 186, 527–543 (1994).
Schütte, C. & Garst, M. Magnon-skyrmion scattering in chiral magnets. Phys. Rev. B 90, 094423 (2014).
Ezawa, M. Compact merons and skyrmions in thin chiral magnetic films. Phys. Rev. B 83, 100408 (2011).
Laidler, K. J. & King, M. C. The development of transition-state theory. J. Phys. Chem. 87, 2657–2664 (1983).
Kramers, H. A. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 7, 284–304 (1940).
Dupé, B., Bihlmayer, G., Blügel, S. & Heinze, S. Engineering skyrmions in transition-metal multilayers for spintronics. Preprint at arXiv:1503.08098v1 (2015).
Krause, S. et al. Magnetization reversal of nanoscale islands: How size and shape affect the Arrhenius prefactor. Phys. Rev. Lett. 103, 127202 (2009).
Acknowledgements
Financial support from the DFG in the framework of the SFB668 is gratefully acknowledged. We thank A. Kubetzka, S. Krause and A. Butenko for discussions.
Author information
Authors and Affiliations
Contributions
E.Y.V. proposed the concept of the investigation. J.H. performed the MC calculations. N.R. carried out the SP-STM measurements on Pd/Fe/Ir(111). All authors discussed the results and prepared the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-3, Supplementary Notes 1-3 and Supplementary References (PDF 645 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Hagemeister, J., Romming, N., von Bergmann, K. et al. Stability of single skyrmionic bits. Nat Commun 6, 8455 (2015). https://doi.org/10.1038/ncomms9455
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms9455
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.