Abstract
Pressure- and temperature-induced phase transitions have been studied for more than a century but very little is known about the non-equilibrium processes by which the atoms rearrange. Shock compression generates a nearly instantaneous propagating high-pressure/temperature condition while in situ X-ray diffraction (XRD) probes the time-dependent atomic arrangement. Here we present in situ pump–probe XRD measurements on shock-compressed fused silica, revealing an amorphous to crystalline high-pressure stishovite phase transition. Using the size broadening of the diffraction peaks, the growth of nanocrystalline stishovite grains is resolved on the nanosecond timescale just after shock compression. At applied pressures above 18 GPa the nuclueation of stishovite appears to be kinetically limited to 1.4±0.4 ns. The functional form of this grain growth suggests homogeneous nucleation and attachment as the growth mechanism. These are the first observations of crystalline grain growth in the shock front between low- and high-pressure states via XRD.
Similar content being viewed by others
Introduction
Predicting the atomistic structure of materials under conditions of extreme pressure and temperature1 using state-of-the-art simulation capabilities currently cannot address the timescale and mechanistic pathway of material phase transitions. Understanding the time dependence of material phase transitions has been a continued area of scientific research since the observation of shock wave propagation associated with the α–ɛ phase transition in iron2,3. A shock wave, the fastest mechanical loading that can be applied to a material, provides a nearly instantaneous change in thermodynamic conditions from which material-based dynamics controlling transitions between state or physical properties, can be measured. At the macroscopic level, Dolan et al.4 demonstrated the complexity and time dependence of a material phase transition by measuring changes in the index of refraction via optical imaging of shock-compressed water. However, obtaining atomistic data in the non-equilibrium state during the process of a material phase transition has remained elusive until now.
To understand the fundamental physics that govern atomic interactions, measurements are required at the relevant timescale and length scale. X-ray diffraction (XRD) has been used for over a century to study the atomic structure and more recently the structural changes associated with the application of pressure and temperature. The application of XRD to shock-induced phase transitions began with Johnson and Mitchel5 on single crystals, demonstrating the ability to measure structural changes during dynamic compression. More recently, studies on dielectrics (for example, refs 6, 7) and semiconductors or metals (for example, refs 8, 9, 10, 11, 12) have observed atomic structural transitions via nanosecond time-resolved XRD, in some cases constraining the atomic pathways, for crystalline–crystalline phase transitions. Recent in situ XRD experiments using short-pulse X-ray probes combined with laser-induced shocks13 investigated the atomistic strain time dependence associated with stress-induced plastic relaxation processes—a process too rapid to be diagnosed by other means14. Ongoing work using in situ XRD measurements has contributed to our understanding and interpretation of continuum wave profile measurements of shock-induced phase transitions15,16.
Using the high-brightness short-pulse Linac Coherent Light Source (LCLS) X-ray free-electron laser (XFEL) we report the first results of shock-induced nanosecond nucleation and growth of a high-pressure crystalline phase from initially amorphous material. Debye–Scherrer patterns are recorded during the transit of a shock wave through fused silica (SiO2). Temporally resolved XRD patterns clearly demonstrate the growth of crystalline stishovite out of the original amorphous fused silica. We measure the diffraction peaks widths that provide information on the size, and hence rate of growth of the nano-crystallites that form. Though a disorder to ordering process is expected to be slow, we find that the stishovite grains nucleate and grow rapidly, within the first few nanoseconds, and the growth trend supports a coalescence growth model rather than a diffusion-based mechanism. These data and present analysis are the first demonstration of shock-induced crystallization of an amorphous material via femtosecond diffraction and will lead to a greater understanding of important problems in shock physics and their relation to geophysics.
Results
In situ XRD
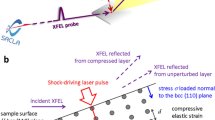
Atomic structure measurements of uniaxially shock-compressed fused silica were made using transmission in situ XRD with 8 keV X-rays from the XFEL at the Matter in Extreme Conditions end-station of the LCLS (Fig. 1). XRD from each pump–probe experiment, recorded on the Cornell-SLAC Pixel Array Detectors (CSPADs) (Supplementary Figure 1), is azimuthally integrated as a function of X-ray scattering angle (2θ) (see Methods). The applied pressure P from laser ablation was determined using the known fused silica principal Hugoniot17 and shock speed (Supplementary Methods, VISAR Analysis Details). Applied pressures of 33.6±5.0, 18.9±3.0, 7.6±1.2 and 4.7±0.8 GPa were set by the incident laser intensity. XRD measurements are spatially integrated over the whole sample and therefore the diffraction measures varying contributions from ambient and compressed SiO2 as a function of time due to the shock wave propagation. Time zero is defined as the time when the shock wave enters the SiO2.
The lattice response of the sample was captured in a Debye–Scherrer geometry. Inset: example of XRD resulting from azimuthal integration of CSPAD data for a suite of time delays under shock compression. A schematic of the target is shown on the right side for each time delay (white: plastic; grey: fused silica). A dashed line indicates the approximate location of the shock front; arrow is the shock propagation direction.
Diffraction observations
A first sharp diffraction peak (FSDP) from fused silica (starting density, 2.20 g cm−3) is centred at 2θ∼21.6°, consistent with previous work18 at ambient conditions. The observed intensity of this FSDP decreases with increasing pump–probe delay time. At the lower applied pressures the FSDP shifts to smaller d-spacing, indicative of a compressed amorphous material, before the phase transition initiates. The high-pressure phase is observed by the formation of azimuthally (about the X-ray beam axis) symmetric crystalline diffraction rings that are indexed as octahedrally coordinated high-pressure crystalline stishovite (tetragonal, P42/mnm). The relative intensities of the first four Bragg reflections (110), (101), (111) and (210) and azimuthal symmetry show no preferred orientation (that is, intensities are comparable to powder diffraction19). Details of Rietveld refinements of example diffraction patterns are shown in Supplementary Figure 2 and Supplementary Methods: Rietveld Refinements.
At 33.6 GPa time-resolved snapshots show the structural changes (Fig. 1) during the reconstructive transformation to stishovite (density measurement, 4.61(7) g cm−3, is consistent with previous work20). By 3.6 ns, the data show the clear emergence of crystalline stishovite peaks. With increasing probe delay time, the intensity of these diffracted peaks increases as the shock front moves further into the sample and the XFEL beam probes a larger volume fraction of the high-pressure stishovite phase. Figure 2 shows the integrated diffraction data for each applied pressure and delay time.
Stishovite peaks are labelled at the top; ambient condition positions (grey dashed lines). Traces are clustered according to applied pressure where each colour indicates a different delay time (grey is X-ray only). Offset along the y axis is arbitrary for viewing clarity. Discontinuities in the traces are seen at 32.5°, 46.0° and 58.0° 2θ due to spacing between the application-specific integrated circuits of the CSPADs.
XRD patterns at 4.7 and 7.6 GPa show a super-positioning of a very broad peak centred at 2θ=30.4° (±0.3) and the emergence of a narrow peak fitting the (110) position of stishovite at later time delays. We interpret this as observing first the compression of the amorphous silica, as documented by a shift in the FSDP to smaller d-spacing, followed by the onset of stishovite by 3.7–9.3 ns delay times. The appearance of stishovite at the lower applied pressure is within the stability field of coesite as determined from static compression work (Supplementary Methods: Diffraction Interpretation Details).
Peak width analysis
The geometry-related peak broadening of the Debye–Scherrer cones projected on the CSPADs is corrected and the instrumental broadening measured using a CeO2 powder standard (Supplementary Fig. 2 and Supplementary Methods: Rietveld Refinements). Peak widths of the stishovite are markedly broader than the standard. The extra broadening is interpreted as coming from a combination of size and strain broadening. The average grain size and root mean squared (r.m.s.) strain distribution can be extracted from the data by using a modified Warren–Averbach21 analysis. For our analysis, a symmetric strain profile is assumed and each peak is fit with a Gaussian distribution:  , where g is the scattering vectors centred at lattice plane (hkl), whose inverse plane spacing (Qhkl) and peak width W is related by: W2=B2+A2Qhkl2 (Fig. 3). Peak width parameters A and B are related to strain and grain size, repectively11. A weighted linear fit to W2 plotted as a function of Qhkl2 provides the value for the y intercept:
, where g is the scattering vectors centred at lattice plane (hkl), whose inverse plane spacing (Qhkl) and peak width W is related by: W2=B2+A2Qhkl2 (Fig. 3). Peak width parameters A and B are related to strain and grain size, repectively11. A weighted linear fit to W2 plotted as a function of Qhkl2 provides the value for the y intercept:  , where σ is an average grain size, and the slope:
, where σ is an average grain size, and the slope:  , where
, where  is the r.m.s. strain assuming a Gaussian strain distribution within the grains probed (Supplementary Methods: Grain Size Determination). At early times we see 1 (±0.5) % r.m.s. variations in strain reducing at later times to 0.1 (±0.06) % r.m.s.
is the r.m.s. strain assuming a Gaussian strain distribution within the grains probed (Supplementary Methods: Grain Size Determination). At early times we see 1 (±0.5) % r.m.s. variations in strain reducing at later times to 0.1 (±0.06) % r.m.s.
Q is related to the 2θ peak position by:  ; X-ray wavelength λ=1.5498 Å. Dots are the measured points and the lines are the weighted linear fits. Colour code is the same as in Fig. 2. The lack of more than one Bragg peak at a given time delay for the 4.7 and 7.6 GPa data limits our ability to directly measure the slope. Therefore, the A parameter determined from the 7.6-GPa, 9.7-ns shot (yielding a r.m.s. strain of 10−3) is used for all other 4.7- and 7.6-GPa traces, providing an upper bound on the grain size. For the 18.9- and 33.6-GPa shots ɛ decreases with increasing delay time from 10−3 to 10−4.
; X-ray wavelength λ=1.5498 Å. Dots are the measured points and the lines are the weighted linear fits. Colour code is the same as in Fig. 2. The lack of more than one Bragg peak at a given time delay for the 4.7 and 7.6 GPa data limits our ability to directly measure the slope. Therefore, the A parameter determined from the 7.6-GPa, 9.7-ns shot (yielding a r.m.s. strain of 10−3) is used for all other 4.7- and 7.6-GPa traces, providing an upper bound on the grain size. For the 18.9- and 33.6-GPa shots ɛ decreases with increasing delay time from 10−3 to 10−4.
Discussion
Tabulated average grain sizes plotted as a function of probe times (Fig. 4) show the nucleation and growth of the high-pressure phase. Similar to other nanocrystalline growth22 the evolution of the mean particle size versus time resembles the trend predicted by classical growth models23 where the size of the particles, D, is proportional to growth time t. A description similar to Huang et al.24 is used: D=k(t−t0)1/n where k(T) is a temperature (T)-dependent material constant appropriate to exponent n, and t0(P) is nucleation time. n is associated with transformation and growth mechanisms24,25,26, that is, when n≤4 growth is diffusion related, however, if n>4, growth could be described by attachment or coalescence events. The data were fit with a single best-fit value of n=7 for all applied pressures, indicating perhaps a coalescence grain growth regime due to homogenous nucleation27 is most appropriate for the stishovite. k(T) and t0(P) are expected to vary with applied shock pressure by the change in thermodynamic state. The t0 decreases and k(T) parameter increases with increasing applied pressure (and therefore increasing temperature). There is little difference in the observed nucleation time (1.4 ns), growth rate or plateau for 18.9 and 33.6 GPa data, suggesting that the higher applied pressure shots are kinetically limited in the nucleation and growth of stishovite (for fitting details see Supplementary Methods: Grain Growth Model).
Different colours/symbols are for SiO2 at different applied pressures. Fits are from a simple growth model. Cartoon on the right (for 33.6 GPa at 10-ns delay, grey box) illustrates our interpretation of grain growth behind the shock front (black dashed line, propagation direction is grey arrow) showing a distribution of grain size increasing with distance from the shock front. A qualitative trend for probable grain density23 as function of time (or distance) is also shown.
Our results clearly show the majority of the sample becomes stishovite during shock compression. Compared with temperature-only driven studies (for example, ref. 28) looking at nucleation and growth of crystallites from amorphous starting samples, our experiments probed shorter length- and timescales, where we see order of magnitude faster growth and smaller grains. In fact, the timescale for stishovite nucleation is surprisingly fast, in particular at the higher applied stresses, it is markedly faster than what is expected for a diffusion-mediated process27. Other diffusionless transformations (that is, martensitic transitions in iron16,27) take place in a few nanoseconds or less. Reconstructive transitions are thought to be diffusive in nature5, however we have shown the mechanism of transformation may be better suited by coalescence events in a homogeneous nucleation regime.
Stishovite is found at bolide-impact craters on the Earth’s surface presumably generated by a shock wave process. And contrary to some studies concluding that a dense amorphous phase, rather than crystalline stishovite forms along the SiO2 Hugoniot29, we have shown on the laboratory timescale, we directly observe formation and growth of stishovite. Shock recovery experiments only find a trace amount of stishovite30 but the material goes through a release pathway. Therefore, our new data on stishovite forming on compression may constrain the formation of the diaplectic (sixfold coordinated) glass and coesite to the release path—an important clue to unravelling the impact history of Earth and the solar system.
Methods
Experimental setup
Using the Matter in Extreme Condtions instrument at the LCLS31, quasi-monochromatic (dE/E=0.2–0.5%), fully transverse coherent, 7.952(30) keV X-ray pulses of 60-fs duration with an average of ∼1012 photons per pulse, were incident over a 75-μm diameter spot on the target package. Wafers of amorphous Nikon synthetic fused silica (SiO2) prepared by melt quenching were double-side parallel polished to a thickness of 60 μm and diced into 2 × 2 mm individual targets. The wafers include tens of parts per million (p.p.m.) values of OH and Cl with <1 p.p.m. for other cations. These targets were batch coated with 10 μm of plastic (glow discharge polymer deposition of trans-2-butene, 1C:1.3H (ref. 32)) to serve as the ablator. An X-ray-only shot was collected before each drive shot as a reference. The 75-μm XFEL beam spot did not produce any observable X-ray damage to the target. Using phase plates on the optical drive laser, a 200-μm diameter flat-top laser spot was used to achieve focal spot intensity of ∼1012 W cm−2. The angle between drive laser arms and XFEL probe is 6°. An ablation-driven compression wave was launched parallel to the sample normal over a 10-ns quasi-square pulse profile from a frequency-doubled Nd:Glass laser system (λ=527 nm). The optical laser and X-ray beam were spatially overlapped and operated in single-shot mode. The absolute time zero corresponds to overlap of their leading edges. For each shot, a time delay was selected for the XFEL pulse relative to the optical laser pulse with a jitter of 0.3–0.5 ns (which is displayed as the temporal uncertainty for Fig. 4). This delay time was verified by oscilloscope traces captured for each shot. For the purposes of discussing the kinetics in the SiO2 only, we establish a relative time zero defined as the time at which the pressure wave reaches the interface between the plastic ablator and the SiO2. The transit time through the plastic ablator varies as a function of drive energy and was determined from VISAR measurements (see Supplementary Methods: VISAR Analysis Details). The combined use of a pressure–irradiance scaling and the transit time provides constraints on the applied pressure for each shot. The pump–probe delay scans at several nanosecond intervals enabled collection of a time series of XRD patterns in transmission geometry. XRD patterns were captured by CSPADs constructed of individual application-specific integrated circuits33. Maximum azimuthal angle coverage was 23°. One target was shot per time delay selected.
Diffraction normalization
Background subtraction and normalization of each trace to volume shocked was explored. First, a dark pattern without X-rays was subtracted from every trace (examples of darks and ambient condition SiO2 traces given in Supplementary Fig. 3). I is the normalized intensity (equal to the integrated intensity of the entire sample) with a contribution from each region of the target: a (ablator), u (unshocked SiO2) and s (shocked SiO2). We found the signal from the plastic ablator (Ia) only contributed ∼25 counts on the CSPADs, and is therefore taken to be negligible in the normalization calculations, therefore, Ibkgd=Iu is determined from the X-ray-only pre-shot trace. Defining nu as the fraction of SiO2 unshocked and ns=1−nu as the fraction of SiO2 shocked, the signal from a shot (Isig) is defined as Isig=Iunu+Isns. Therefore, the normalization factor (Isig−nuIbkgd)/ns, applied to every trace in Fig. 2 gives Supplementary Fig. 4. However, due to uncertainties in the contribution of the background shot to shot we cannot accurately determine the phase fraction of the individual components, that is, uncompressed amorphous, compressed amorphous or stishovite, and therefore only estimate the relative intensities of the uncompressed region to compressed region.
Additional information
How to cite this article: Gleason, A. E. et al. Ultrafast visualization of crystallization and grain growth in shock-compressed SiO2. Nat. Commun. 6:8191 doi: 10.1038/ncomms9191 (2015).
Change history
13 October 2015
An incorrect version of the Supplementary Information was inadvertently published with this Article and did not show axes labels for Supplementary Figures 2-4. The HTML has now been updated to include the correct version of the Supplementary Information.
References
Bridgman, P. W. Recent work in the field of high pressures. Rev. Mod. Phys. 18, 1–95 (1946).
Bridgman, P. W. High pressure polymorphism of iron. J. Appl. Phys. 27, 659 (1956).
Bancroft, D., Peterson, S. & Minshall, S. Polymorphism of iron at high pressure. J. Appl. Phys. 27, 291–298 (1956).
Dolan, D., Johnson, J. & Gupta, Y. Nanosecond freezing of water under multiple shock wave compression: continuum modeling and wave profile measurements. J. Chem. Phys. 123, 064702 (2005).
Johnson, Q. & Mitchell, A. First X-ray diffraction evidence for a phase transition during shock-wave compression. Phys. Rev. Lett. 29, 1369–1371 (1972).
Gupta, Y. et al. Experimental developments to obtain real-time X-ray diffraction measurements in plate impact experiments. Rev. Sci. Instrum. 70, 4008–4014 (1999).
Turneaure, S., Gupta, Y. & Rigg, P. Shock induced phase change in KCl single crystals: orientation relations between the B1 and B2 lattices. J. Appl. Phys. 105, 013544 (2009).
Wark, J., Whitlock, R., Hauer, A., Swain, J. & Solone, P. Shock launching in silicon studied with use of pulsed X-ray diffraction. Phys. Rev. B 35, 9391–9394 (1987).
Kalantar, D., Belak, J., Collins, G., Colvin, J. & Davies, H. et al. Direct observation of the a-e transition in shock-compressed iron via nanosecond X-ray diffraction. Phys. Rev. Lett. 95, 075502 (2005).
Hawreliak, J., Colvin, J., Eggert, J., Kalantar, D. & Lorenzana, H. et al. Analysis of the X-ray diffraction signal for the a-e transition in shock-compressed iron: simulation and experiment. Phys. Rev. B 74, 184107 (2006).
Hawreliak, J. et al. High-pressure nanocystalline structure of a shock-compressed single crystal of iron. Phys. Rev. B 78, 220101 (2008).
Turneaure, S. & Gupta, Y. Real-time microstructure of shock-compressed single crystals from X-ray diffraction line profiles. J. Appl. Cryst. 44, 574–584 (2011).
Milathianaki, D., Boutet, S., Williams, G., Higginbotham, A. & Ratner, D. et al. Femtosecond visualization of lattice dynamics in shock-compressed matter. Science 342, 220–223 (2013).
Loveridge-Smith, A., Allen, A., Belak, J., Boehly, T. & Hauer, A. et al. Anomalous elastic response of silicon to uniaxial shock compression on nanosecond time scales. Phys. Rev. Lett. 86, 2349–2352 (2001).
Jensen, B., Gray, G. & Hixson, R. Direct measurements of the α-ɛ transition stress and kinetics for shocked iron. J. Appl. Phys. 105, 103502 (2009).
Hawreliak, J., El-Dasher, B., Lorenzana, H., Kimminau, G. & Higginbotham, A. et al. In situ X-ray diffraction measurements of the c/a ratio in the high-pressure e phase of shock-compressed polycrystalline iron. Phys. Rev. B 83, 144114 (2011).
Marsh S. (ed.) LASL Shock Hugoniot Data 321–323Univ. of California (1980).
Meade, C., Hemley, R. & Mao, H. K. High-pressure X-ray diffraction of SiO2 glass. Phys. Rev. Lett. 69, 1387–1390 (1992).
Ross, N., Shu, J. F., Hazen, R. & Gasparik, T. High pressure crystal chemistry of stishovite. Am. Mineral. 75, 739–747 (1990).
Wang, F., Tange, Y., Irifune, T. & Funakoshi, K.-i. P-V-T equation of state of stishovite up to mid-lower mantle conditions. J. Geophys. Res. 117, B06209 (2012).
Warren, B. & Averbach, B. The effect of cold-work distortion on X-ray patterns. J. Appl. Phys. 21, 595–599 (1950).
Zheng, H. et al. Observation of single colloidal platinum nanocrystal growth trajectories. Science 324, 1309–1312 (2009).
Fokin, V., Yuritsyn, N. & Zanotto, E. in Nucleation Theory and Applications ed. Schmelzer J. 74–125Wiley-VCH (2005).
Huang, F., Zhang, H. & Banfield, J. Two-stage crystal-growth kinetics observed during hydrothermal coarsening of nanocrystalline ZnS. Nano Lett. 3, 373–378 (2003).
Kirchner, H. Coarsening of grain-boundary precipitates. Metall. Trans. 2, 2861–2864 (1971).
Ghasemzadeh, M., Nemati, A., Nozad, A., Hamnabard, Z. & Baghshahi, S. Crystallization kinetics of glass-ceramics by differential thermal analysis. Ceramics 55, 188–194 (2011).
Kadau, K., Germann, T., Lomdahl, P. & Holian, B. Microscopic view of structural phase transitions induced by shock waves. Science 296, 1681–1684 (2002).
Nikolova, L. et al. Nanocrystallization of amorphous germanium films observed with nanosecond temporal resolution. Appl. Phys. Lett. 97, 203102 (2010).
Panero, W., Benedetti, L. & Jeanloz, R. Equation of state of stishovite and interpretation of SiO2 shock-compression data. J. Geophys. Res. 108, 2015 (2003).
Gratz, A. et al. Shock metamorphism of quartz with initial temperatures -170 to 1000 deg C. Phys. Chem. Minerals 19, 267–288 (1992).
Nagler, B. et al. The matter in extreme conditions instrument at the Linac coherent light source. J. Synchrotron Rad. 22, 520–525 (2015).
Nikroo, A. et al. Progress in 2 mm glow discharge mandrel development for NIF. Fusion Sci. Technol. 45, 165–168 (2004).
Philipp, H., Hromalik, M., Tate, M., Koerner, L. & Gruner, S. Pixel array detector for X-ray free electron laser experiments. Nat. Synchrotron Rad. Instrum. 649, 67–69 (2011).
Acknowledgements
W.L.M. is supported by the Department of Energy, Office of Science, Basic Energy Sciences (DOE-BES), Materials Sciences and Engineering Division, under Contract DE-AC02-76SF00515. A.E.G. was supported by NSF Geophysics (EAR-1446969) and the Edward H. Kraus Crystallographic Research Fund through MSA for partial fabrication costs. We also gratefully acknowledge funding from the LANL LDRD programme. The work by R.G.K., J.H.E., D.E.F., and G.W.C. was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. This work was performed at the Matter at Extreme Conditions (MEC) instrument of LCLS, supported by the US DOE Office of Science, Fusion Energy Science under contract No. SF00515, and was supported by LCLS, a National User Facility operated by Stanford University on behalf of DOE-BES. We thank W.-P. Hsieh, Q. Zeng and LCLS/SLAC staff for assistance during the experiment.
Author information
Authors and Affiliations
Contributions
C.B. participated in the experiment and contributed to the data analysis and interpretation; H.J.L., B.N., E.G. and D.M. each participated in the experiment as instrument scientists at MEC and contributed to data interpretation; J.E., G.C., W.M. and R.S. each contributed to the data analysis and interpretation; J.H. contributed to the data analysis, interpretation and outline of the paper; D.F. and R.K. contributed to the data analysis and interpretation and each provided modelling analysis and support in VISAR interpretation; W.Y. participated in the experiment and contributed to the data analysis by writing software to examine XRD data; A.G. was principal investigator, analysed the data and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-4, Supplementary Table 1, Supplementary Methods and Supplementary References (PDF 1763 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Gleason, A., Bolme, C., Lee, H. et al. Ultrafast visualization of crystallization and grain growth in shock-compressed SiO2. Nat Commun 6, 8191 (2015). https://doi.org/10.1038/ncomms9191
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms9191
This article is cited by
-
Single-shot X-ray absorption spectroscopy at X-ray free electron lasers
Scientific Reports (2023)
-
Materials under extreme conditions using large X-ray facilities
Nature Reviews Methods Primers (2023)
-
Dynamic compression of water to conditions in ice giant interiors
Scientific Reports (2022)
-
Ultrafast olivine-ringwoodite transformation during shock compression
Nature Communications (2021)
-
Simulation and Emulation of X-Ray Diffraction from Dynamic Compression Experiments
Journal of Dynamic Behavior of Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.