Abstract
Water exists in two spin isomers, ortho and para, that have different nuclear spin states. In bulk water, rapid proton exchange and hindered molecular rotation obscure the direct observation of two spin isomers. The supramolecular endofullerene H2O@C60 provides freely rotating, isolated water molecules even at cryogenic temperatures. Here we show that the bulk dielectric constant of this substance depends on the ortho/para ratio, and changes slowly in time after a sudden temperature jump, due to nuclear spin conversion. The attribution of the effect to ortho–para conversion is validated by comparison with nuclear magnetic resonance and quantum theory. The change in dielectric constant is consistent with an electric dipole moment of 0.51±0.05 Debye for an encapsulated water molecule, indicating the partial shielding of the water dipole by the encapsulating cage. The dependence of bulk dielectric constant on nuclear spin isomer composition appears to be a previously unreported physical phenomenon.
Similar content being viewed by others
Introduction
Water, like dihydrogen, has two different spin isomers, called ortho and para, which have different spin state symmetries. In ortho-water, the spin state of the two proton nuclei is symmetric under particle exchange and the total nuclear spin has quantum number I=1. In para-water, the spin state is antisymmetric and has nuclear spin quantum number I=0. Water spin isomerism is of relevance to a broad range of scientific fields from nuclear magnetic resonance (NMR) to astrophysics1,2,3,4,5, and closely related to long-lived nuclear spin states, which also involve the slow interconversion of nuclear singlet and triplet states6,7.
Physical properties of dihydrogen H2, such as heat capacity or thermal conductivity, depend on the concentration of ortho and para spin isomers8. Do the spin isomers of water also have different bulk properties? Since water, unlike dihydrogen, possesses an electric dipole moment, the spin isomers of ortho and para water are expected to display a distinct response to electric fields. This effect was predicted theoretically9; and observed in beam experiments10, but no bulk properties have been reported.
Although it is feasible to separate ortho- and para-water molecules in rarified molecular beams5,10, it remains challenging to study the separated isomers in the condensed phase, since rapid proton exchange obscures the spin isomerism in bulk water, and strong intermolecular interactions usually quench the molecular rotation at low temperatures. Spin isomer-enriched water may be captured in an inert gas matrix and studied using infrared spectroscopy11,12, but this approach provides little control over the molecular environment.
In contrast, the supramolecular endofullerene H2O@C60, composed of C60 carbon cages that each encloses a single water molecule, forms a well-defined lattice. The synthesis of this material provides macroscopic quantities of a stable substance that contains isolated and freely rotating water molecules13,14. It has been studied under a very wide range of physical conditions using various spectroscopic techniques1,2,5. Dielectric measurements were made on a single crystal of H2O@C60, but without anticipating, or observing, a dependence on spin isomer composition15.
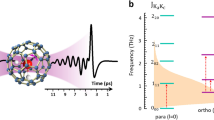
Figure 1a,b shows the molecular structure of H2O@C60 and the four lowest rotational energy levels as determined by neutron scattering, neglecting the observed splitting of the ortho-water ground state1,3. The energy levels are similar to those of water in the gas phase indicating that the water rotation is unhindered even at cryogenic temperatures. The thermal equilibrium fraction of ortho-water molecules as a function of temperature is shown in Fig. 1c, using the energy levels of Fig. 1b and taking into account the degeneracies of the rotational levels2,16. The equilibrium fraction changes rapidly in the vicinity of 15 K. Ortho–para conversion may therefore be induced by (i) allowing the sample to reach complete equilibrium at a temperature >15 K, (ii) rapidly cooling to <15 K and (iii) studying the behaviour of the sample as a function of time at the constant low temperature.
Here we demonstrate that the bulk dielectric constant of H2O@C60 depends on the spin isomer composition of the encapsulated water molecules. We find a time-dependent change in dielectric constant at 5 K that is due to different molecular polarizabilities of the ortho and para ground states. The polarizabilities are extracted from the capacitance data and compared with a theoretical prediction that only requires knowledge of the dipole moment of H2O@C60 and the rotational constants of water. The dipole moment is estimated from a high-temperature measurement of the molecular polarizability and found to be in very good agreement with recent predictions of 0.5±0.1 Debye17,18,19.
Results
Dielectric constant
The dielectric response of water on ortho–para conversion is demonstrated with the apparatus shown in Fig. 2 (see Supplementary Methods for details). Three capacitors are measured simultaneously: one is filled with a 4:1 homogeneous mixture of H2O@C60 and C60, one is filled with pure C60, and one is left empty. The apparatus was used to measure (1) the variation of dielectric constant with time at low temperature, which is related to ortho–para conversion and (2) the variation of dielectric constant with temperature above 50 K. The low-temperature experimental data are shown in Fig. 2c–f. Following equilibration at 25 K, the temperature is rapidly decreased to 5 K and stabilized within ±30 mK for the remaining time of the experiment. The capacitance of the H2O@C60 cell decreases over approximately 50 h. No significant variation is observed for the capacitor filled with pure C60, or the empty capacitor. All measurements are performed at constant frequency and temperature, so that ortho–para conversion is the only process that can account for the decay shown in Fig. 2c. Other possible influences such as geometric drift or gradual penetration of liquid helium into the cell may be discounted since the pure C60 and empty capacitors do not show similar behaviour.
(a) Photograph and (b) exploded view of the sample cell consisting of two printed circuit boards (PCBs, green) and a 210 μm thick G10 spacer used to centre the sample pellets between the electrodes of the two PCBs, forming three independent capacitor cells. Scale bar length in a is 2 cm. Following a temperature jump from 25 to 5 K at the time origin, the capacitance of the three cells is measured as a function of time. (c) The capacitance of the cell loaded with H2O@C60 decreases monotonically due to ortho–para conversion. The capacitances of (d) the empty cell and (e) the cell loaded with C60 change slightly as the temperature is changed, but are constant after the temperature jump. The temperature measurement is shown in f.
Nuclear magnetic resonance
Proton NMR measurements provide an independent measure of nuclear spin conversion in H2O@C60 since the 1H NMR signal is proportional to the ortho spin isomer fraction Φ. At a temperature of 5 K, the spin isomer conversion takes many hours and follows second-order kinetics2. The 600 MHz proton NMR signal amplitude after rapid sample cooling from 25 to 5 K was measured in a magnetic field of 14.1 T using a separate apparatus but the same sample batch as the one used for the capacitance measurements. The NMR signal is shown in Fig. 3 (black points). The NMR results show a small but significant ortho fraction persisting even after 40 h at 5 K. The reasons for the metastable ortho fraction in this sample batch are currently unknown.
The results of NMR and capacitance measurements are compared in Fig. 3. As described in the Supplementary Discussion, the NMR data were shifted in time by 2.2 h with respect to the capacitance data to take into account the smaller ortho fraction at the time the final temperature is reached in the NMR experiment, compared to the capacitance measurement. This difference in initial ortho fraction is due to the slower cooling rate of the NMR probe compared to the capacitance probe, which leads to an initial depletion of the ortho fraction through the enhanced ortho–para conversion rate at high temperature2,20. The similar behaviour of the capacitance and NMR data strongly supports the conclusion that the decay in dielectric constant of H2O@C60 is due to nuclear spin isomer conversion (see Supplementary Discussion).
The NMR signal intensity and the dielectric constant both display a rapid initial increase on sample cooling. However these rapid initial changes have a different origin in the two measurements. In NMR, ortho-water gives rise to a signal and para-water does not. The NMR signal of ortho-water depends on the polarization of the Zeeman substates of each ortho level. The Zeeman polarization, and hence the NMR signal, follow the Curie law in this temperature regime and increase on decreasing temperature. As detailed in the Supplementary Discussion and Supplementary Fig. 4, the dielectric constant also follows a Curie law at higher temperatures, but strong deviations are observed at low temperatures where only a few rotational states are populated.
Discussion
The dielectric constants of the H2O@C60/C60 sample and the pure C60 sample may be calculated from the known geometry of the capacitors. From the dielectric constant one can estimate the microscopic molecular polarizability of H2O@C60. We denote the molecular polarizabilities of C60 filled with H2O by α· and of empty C60 by α○, and the corresponding volume densities by N· and N○, respectively. The molecular polarizabilities are linked to the dielectric constant by the Clausius-Mossotti relation21:

Knowledge of the empty cage polarizability α○ and the empty and filled cage volume densities N○ and N· enables one to compute α·, the molecular polarizability of H2O@C60. To study the effect of the encapsulation of water in C60, we measured the capacitance of the three cells as a function of temperature between 50 and 250 K, and used the Clausius-Mossotti relationship to estimate the molecular polarizabilities for both C60 and H2O@C60. These data are interpreted in terms of a temperature-independent deformation polarizability, plus a temperature-dependent orientational polarizability associated with partial molecular alignment along an applied electric field22. In agreement with previous reports23 we find a deformation polarizability volume for empty C60 of  of 87±5 Å3 and additionally a weak thermally activated polarizability volume of 5±1 Å3 at low temperature24 (see Supplementary Fig. 1 and Supplementary Discussion). For H2O@C60, the molecular polarizability may be written as α·=α○+α·orient+Δα∞, where α·orient denotes the orientational polarizability due to the water dipole moment and Δα∞ corresponds to a change in deformation polarizability. The observed change in deformation polarizability is Δα∞=17±3 Å3; significantly larger than a recent theoretical prediction18. The reasons for the discrepancy are currently unknown. The orientational polarizability α·orient, shown in Supplementary Fig. 2, is found to follow a Debye relationship corresponding to a dipole moment of μ=0.51±0.05 Debye.
of 87±5 Å3 and additionally a weak thermally activated polarizability volume of 5±1 Å3 at low temperature24 (see Supplementary Fig. 1 and Supplementary Discussion). For H2O@C60, the molecular polarizability may be written as α·=α○+α·orient+Δα∞, where α·orient denotes the orientational polarizability due to the water dipole moment and Δα∞ corresponds to a change in deformation polarizability. The observed change in deformation polarizability is Δα∞=17±3 Å3; significantly larger than a recent theoretical prediction18. The reasons for the discrepancy are currently unknown. The orientational polarizability α·orient, shown in Supplementary Fig. 2, is found to follow a Debye relationship corresponding to a dipole moment of μ=0.51±0.05 Debye.
The enhanced deformation polarizability of H2O@C60 may be used to calculate its orientational polarizability volume at low temperatures (Supplementary Fig. 3). As detailed in the Supplementary Discussion, the time-dependent capacitance and NMR data may be combined to estimate the individual polarizability volumes of the ortho and para ground states. We obtain αortho′=43±5 Å3 and αpara′=29±3 Å3. These results are in acceptable agreement with the theoretical estimates of 32±6 Å3 and 23±5 Å3 for the ortho and para polarizability volumes of the free rotor states obtained by quantum theory16,25, as implemented in the CMIStark software package26, taking into account the reduced dipole moment of 0.51±0.05 Debye (see Supplementary Fig. 4, Supplementary Table 1 and Supplementary Discussion). The relationship between the orientational polarizability and the free rotor wavefunctions is discussed in ref. 26.
The observed change in the bulk dielectric constant, as encapsulated water converts from the ortho to the para spin isomer, is due to a change in molecular polarizability on spin conversion, with conversion kinetics in agreement with previous NMR studies. Separate molecular polarizabilities for the ortho and para ground states are extracted from the experimental data. The dipole moment of H2O@C60 has been measured experimentally and is found to be in good agreement with recent computational predictions17,18,19. A calculation of the ortho and para ground state polarizabilities based on this dipole moment yields good agreement with the capacitance data. The different response of ortho and para water to electric fields provides a sensitive alternative means to study the spin isomers. The phenomenon opens up the prospect of using Kelvin probe force microscopy27 to study water spin isomers on a single-molecule level.
Additional information
How to cite this article: Meier, B. et al. Electrical detection of ortho–para conversion in fullerene-encapsulated water. Nat. Commun. 6:8112 doi: 10.1038/ncomms9112 (2015).
References
Beduz, C. et al. Quantum rotation of ortho and para-water encapsulated in a fullerene cage. Proc. Natl. Acad. Sci. USA 109, 12894–12898 (2012).
Mamone, S. et al. Nuclear spin conversion of water inside fullerene cages detected by low-temperature nuclear magnetic resonance. J. Chem. Phys. 140, 194306 (2014).
Goh, K. S. K. et al. Symmetry-breaking in the endofullerene H2O@C60 revealed in the quantum dynamics of ortho and para-water: a neutron scattering investigation. Phys. Chem. Chem. Phys. 16, 21330–21339 (2014).
Encrenaz, T. Water in the Solar System. Annu. Rev. Astro. Astrophys. 46, 57–87 (2008).
Kravchuk, T. et al. A magnetically focused molecular beam of ortho-water. Science 331, 319–321 (2011).
Carravetta, M., Johannessen, O. G. & Levitt, M. H. Beyond the T1 limit: singlet nuclear spin states in low magnetic fields. Phys. Rev. Lett. 92, 153003 (2004).
Levitt, M. H. Singlet Nuclear Magnetic Resonance. Annu. Rev. Phys. Chem. 63, 89–105 (2012).
Farkas, A. Orthohydrogen, Parahydrogen and Heavy Hydrogen. The Cambridge Series of Physical Chemistry Cambridge University Press (1935).
Andreev, S. N., Makarov, V. P., Tikhonov, V. I. & Volkov, A. A. Ortho and Para Molecules of Water in Electric Field. Preprint at http://arxiv.org/abs/physics/0703038 (2007).
Horke, D. A., Chang, Y. P., Długołecki, K. & Küpper, J. Separating para and ortho water. Angew. Chem. Int. Ed. 53, 11965–11968 (2014).
Turgeon, P. A. et al. Preparation, isolation, storage, and spectroscopic characterization of water vapor enriched in the ortho-H2O nuclear spin isomer. Phys. Rev. A. 86, 62710 (2012).
Redington, R. L. & Milligan, D. E. Molecular rotation and ortho–para nuclear spin conversion of water suspended in solid Ar, Kr, and Xe. J. Chem. Phys. 39, 1276 (1963).
Kurotobi, K. & Murata, Y. A single molecule of water encapsulated in fullerene C60. Science 333, 613–616 (2011).
Krachmalnicoff, A., Levitt, M. H. & Whitby, R. J. An optimised scalable synthesis of H2O@C60 and a new synthesis of H2@C60 . Chem. Commun. 50, 13037–13040 (2014).
Aoyagi, S. et al. A cubic dipole lattice of water molecules trapped inside carbon cages. Chem. Commun. 50, 524–526 (2014).
Bunker, P. R. & Jensen, P. Molecular Symmetry and Spectroscopy 2nd revised edn Canadian Science Publishing (NRC Research Press) (2006).
Ensing, B., Costanzo, F. & Silvestrelli, P. L. On the polarity of buckminsterfullerene with a water molecule inside. J. Phys. Chem. A 116, 12184–12188 (2012).
Galano, A., Pérez-González, A., del Olmo, L., Francisco-Marquez, M. & León-Carmona, J. R. On the chemical behavior of C60 hosting H2O and other isoelectronic neutral molecules. J. Mol. Model 20, 2412–2412 (2014).
Sabirov, D. S. Polarizability as a landmark property for fullerene chemistry and materials science. RSC Adv. 4, 44996–45028 (2014).
Cacciani, P., Cosléou, J. & Khelkhal, M. Nuclear spin conversion in H2O. Phys. Rev. A 85, 012521 (2012).
Atkins, P. & de Paula, J. Atkins’ Physical Chemistry Oxford University Press (2010).
Jackson, J. D. Classical Electrodynamics Wiley (1999).
Bonin, K. D. & Kresin, V. V. Electric-dipole Polarizabilities of Atoms, Molecules, and Clusters World Scientific Publishing Company Incorporated (1997).
Alers, G. B., Golding, B., Kortan, A. R., Haddon, R. C. & Theil, F. A. Existence of an orientational electric dipolar response in C60 single crystals. Science 257, 511–514 (1992).
Zare, R. N. Angular momentum. Understanding Spatial Aspects in Chemistry and Physics Wiley-Interscience (1988).
Chang, Y. P., Filsinger, F., Sartakov, B. G. & Küpper, J. CMIstark: Python package for the Stark-effect calculation and symmetry classification of linear, symmetric and asymmetric top wavefunctions in DC electric fields. Comput. Phys. Commun. 185, 339–349 (2014).
Nonnenmacher, M., O’Boyle, M. P. & Wickramasinghe, H. K. Kelvin probe force microscopy. Appl. Phys. Lett. 58, 2921 (1991).
Acknowledgements
We acknowledge the support of EPSRC-UK (grant number EP/M001962/1), the European Research Council (291044—HYPERSINGLET), and the Wolfson Foundation (WL120007). We thank X. Niu for providing a first version of the PCB spacer. B.M. thanks W. Kossack for useful discussions.
Author information
Authors and Affiliations
Contributions
B.M. constructed the apparatus, performed the experiment, analysed the data and co-wrote the paper. S.M. assisted with the capacitance measurements and data analysis and co-wrote the paper. M.C. and J.A.-V. assisted with capacitance and NMR measurements. A.K. synthesized H2O@C60 guided by R.J.W. and helped with sample preparation. M.H.L. conceived the idea and co-wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-4, Supplementary Table 1, Supplementary Discussion, Supplementary Methods and Supplementary References (PDF 334 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Meier, B., Mamone, S., Concistrè, M. et al. Electrical detection of ortho–para conversion in fullerene-encapsulated water. Nat Commun 6, 8112 (2015). https://doi.org/10.1038/ncomms9112
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms9112
This article is cited by
-
Ortho-para interconversion of nuclear states of H2O through replica transition state: prospect of quantum entanglement at homodromic Bjerrum defect site
Journal of Molecular Modeling (2023)
-
Solid-State \(\mathrm {^3He}\) NMR of the Superconducting Rubidium Endofulleride \(\mathrm {Rb_3(^3He@C_{60})}\)
Applied Magnetic Resonance (2023)
-
Water as a sensor of weak impacts on biological systems
Biophysical Reviews (2023)
-
Effects of Ge, Si, and B doping on the adsorption and detection properties of C60 fullerene towards methadone in gas and aqua phases: a DFT study
Journal of Molecular Modeling (2023)
-
Chemical shielding of H2O and HF encapsulated inside a C60 cage
Communications Chemistry (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.