Abstract
Establishing the appropriate theoretical framework for unconventional superconductivity in the iron-based materials requires correct understanding of both the electron correlation strength and the role of Fermi surfaces. This fundamental issue becomes especially relevant with the discovery of the iron chalcogenide superconductors. Here, we use angle-resolved photoemission spectroscopy to measure three representative iron chalcogenides, FeTe0.56Se0.44, monolayer FeSe grown on SrTiO3 and K0.76Fe1.72Se2. We show that these superconductors are all strongly correlated, with an orbital-selective strong renormalization in the dxy bands despite having drastically different Fermi surface topologies. Furthermore, raising temperature brings all three compounds from a metallic state to a phase where the dxy orbital loses all spectral weight while other orbitals remain itinerant. These observations establish that iron chalcogenides display universal orbital-selective strong correlations that are insensitive to the Fermi surface topology, and are close to an orbital-selective Mott phase, hence placing strong constraints for theoretical understanding of iron-based superconductors.
Similar content being viewed by others
Introduction
Since the discovery of high-temperature superconductivity in the iron pnictides (FePns), extensive research efforts have revealed many common properties of these materials. In the vast material base of the FePns, all parent phases are metallic, and the observed electronic structures are largely consistent with the prediction of ab initio local-density approximation (LDA) calculations1,2. These properties have led to theoretical understanding that the electron correlations in FePns are much weaker than in cuprate superconductors, whose parent phases are Mott insulators. Furthermore, the observation of comparable sized hole pockets at the Brillouin zone (BZ) centre and electron pockets at the BZ corner have resulted in the proposal that such a Fermi surface (FS) topology is ubiquitous and essential to superconductivity in FePns, and pairing in the FePns is mediated by antiferromagnetic fluctuations via FS nesting between the hole and electron Fermi pockets3. On the other hand, there have also been theoretical proposals of ‘incipient Mott localization’ for which the system is metallic but on the verge of localization4,5,6, supported by the normal state bad metal behaviour from optical conductivity measurements7 and the large fluctuating magnetic moment comparable to the antiferromagnetic insulating copper oxides8. This discussion became especially relevant with the more recent discovery of iron chalcogenides (FeChs)9,10,11, which not only possess large local magnetic moments12 and insulating phases13, but also include compounds that lack hole pockets needed for FS nesting yet have comparable superconducting transition temperatures (TCs) as FePns14,15,16,17.
There are currently three major classes of FeCh superconductors: FeTe1−xSex, KxFe2−ySe2, and FeSe film grown on SrTiO3. In the FeTe1−xSex family, superconductivity is achieved with isovalent substitution of Se for Te that suppresses magnetic order in the FeTe end18, and becomes optimal in FeTe0.56Se0.44 (FTS), where TC is 14.5 K. The KxFe2−ySe2 family has in its phase diagram insulating phases with magnetic moments as large as 3.3 μB per Fe10,12,13, and optimal TC is 32 K, such as achieved in K0.76Fe1.72Se2 (KFS). FeSe film grown on SrTiO3 is the latest addition to the FeCh family, with monolayer film (FS/STO) having a record TC possibly exceeding 65 K (refs 11, 16, 17). In a previous angle-resolved photoemission spectroscopy (ARPES) study19 on KFS, we found the low-temperature state to be a metallic state with orbital-dependent renormalization—where the dxy orbital-dominated bands are strongly renormalized as compared with other orbitals. Raising temperature drives the material to an orbital-selective Mott phase (OSMP) in which the dxy orbital completely loses spectral weight while other orbitals remain itinerant. Subsequently, such a temperature scale was also identified by terahertz spectroscopy20, Hall measurements21 and pump–probe spectroscopy22, where the slight temperature scale variations are due to the different definitions used. This motivates the usage of orbital selectivity to address the fundamental open question of whether it is the electron correlation strength or the nature of the FS that plays a predominant role in the microscopic physics of the FeCh materials.
In this work, we study systematically the optimal superconducting members of the three FeCh families, FTS, KFS and FS/STO, using ARPES. We show that, in the low-temperature state, in contrast to the FePns, all of the FeChs are in a strongly correlated regime where strong orbital-selective renormalization is observed on the dxy bands, despite having drastically different FS topologies. In addition, by increasing temperature, all of the FeChs crossover into a phase where the dxy orbital completely loses spectral weight while other orbitals remain metallic. These observations showcase the universally strong orbital-selective electron correlations in the FeChs, and that the superconductivity in the FeChs, which is insensitive to FS topology, occurs in proximity to an orbital-selective Mott phase, placing strong constraints on the theoretical understanding of the iron-based superconductors.
Results
Orbital-selective band renormalization at low temperatures
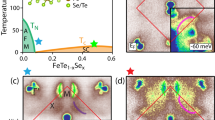
The generic electronic structure of iron-based superconductors (FeSCs) consists of three hole bands at the BZ centre, Γ, and two electron bands at the BZ corner, M. The hole bands are predominantly of dxz, dyz and dxy orbital characters, while the electron bands are dxz and dxy along Γ–M. The relative positions of these bands with respect to each other as well as to the Fermi level (EF) could vary with differences in lattice parameters and doping level. Hence, the FS topology among different FeSCs could be qualitatively different, as shown in Fig. 1a–d, where the Fermi pockets at the BZ centre vary from being hole-like to non-existent to electron like. The measured band structure along the Γ–M high-symmetry direction for the three compounds are shown in Fig. 1e–g, in comparison to that for the optimally Co-doped BaFe2As2 (BFCA) (Fig. 1h), an FePn as a reference. For FTS (Fig. 1i), one of the hole bands crosses EF, and both electron bands cross EF at M, resulting in roughly compensated hole pocket at Γ and electron pockets at M (Fig. 1a), consistent with isovalent substitution for this compound. For both FS/STO (Fig. 1j) and KFS (Fig. 1k) in contrast, only the electron bands cross EF while the hole band tops are well below EF, with an additional small electron pocket at Γ in KFS. Thus, there is heavy electron doping in both compounds as reflected in a FS topology consisting only of electron pockets (Fig. 1b,c). Comparing the band structure of the three FeChs to the FePns, we notice a significant difference near the M point—there is an apparent gap between the bottom of the electron bands and the top of the hole band in all three FeChs, in sharp contrast to BFCA (Fig. 1l), in which the dxz electron band bottom is degenerate with the dyz hole band top.
Fermi surfaces measured on (a) FeTe0.56Se0.44 (FTS), (b) monolayer FeSe film on SrTiO3 (FS/STO), (c) K0.76Fe1.72Se2 (KFS) and (d) Ba(Fe0.93Co0.07)2As2 (BFCA), shown in BZ notation corresponding to 2-Fe unit cell (For comparison purposes, we use the M point to denote the BZ corner where the electron pockets live for all compounds and LDA, even though for 122 crystal structures, this is the X point.), with schematic outlines shown in cyan (magenta) for hole (electron) Fermi pockets. (e) Spectral image of FTS along the Γ–M high-symmetry direction, taken with 22 eV (26 eV) photons for near the Γ (M) point. Measurements along the same cut for (f) FS/STO, (g) KFS and (h) BFCA, with photon energies of 22, 26 and 47.5 eV, respectively. In-plane polarization was odd with respect to the cut for all measurements, (e–g) has additional out-of-plane polarization. (i–l) Second energy derivatives for the spectral images above. Observable bands are marked with dominant orbital character (red: dxz, green: dyz and blue: dxy).
Generally in FeSC, this degeneracy between the dxz electron band bottom and dyz hole band top at the zone corner is protected by the C4 rotational symmetry, as seen in BFCA (Fig. 1l) and corresponding LDA calculations (Fig. 2a). This degeneracy is only lifted with the breaking of C4 symmetry, as in the orthorhombic phase of underdoped BFCA23, NaFeAs24,25, bulk FeSe26,27,28,29 and multilayer FeSe film30,31, where a splitting between the corresponding dxz bands and dyz bands occurs, in addition to a doubling of the bands from twinning effects due to the orthorhombic distortion. However, no static C4 symmetry breaking has been reported for any of the FeChs studied here, nor are twinning effects observed here that is expected from a broken symmetry due to orthorhombic distortion. Rather, this apparent gap can be explained by a strong orbital-dependent band renormalization and band hybridization. As the schematic shown in Fig. 2, the LDA-calculated dxy electron band bottom is deeper than that of the dxz band. If the dxy orbital is strongly renormalized compared with the other orbitals, the dxy electron band bottom, that is, the corresponding dxy hole band top, would rise above that of the dxz electron band (Fig. 2b). The heavily renormalized dxy hole band then crosses the dxz electron band and the two bands hybridize such that a gap appears at the M point without lifting the dxz/dyz degeneracy protected by C4 symmetry (Fig. 2c). Evidence for two nearly degenerate electron bands can be seen in the high-resolution spectra acquired on FS/STO (Fig. 3a). As an aside, we note that in the unrenormalized case (Fig. 2a), a hybridization gap between the dxy electron band and dyz hole band is not observed. This is because when considering the hopping via the chalcogen atoms along this high-symmetry direction (x), both dxy and dxz are odd while dyz is even. Hence dxy does not mix with dyz to produce a hybridization gap32.
(a) LDA calculations for KFS41. (b) Schematic based on a with dxy orbital strongly renormalized. (c) Schematic based on b by introducing hybridization between dxy band and dxz electron band.
(a) High-resolution spectra of FS/STO showing the presence of two electron bands around M. (b) Γ–M high-symmetry cut of FS/STO taken in the second BZ, where dxy orbital matrix elements are strong. The dxy hole band has a lower band top at Γ than dxz/dyz, hence it crosses and hybridizes with the dxz/dyz hole bands, resulting in the apparent sharper curvature near Γ.
This interpretation is further supported by the observed strong renormalization of the dxy hole band near Γ, which is significantly more renormalized than the dxz/dyz hole bands, clearly seen in all three compounds (Fig. 1i–k). For FTS, the dxy hole band is strongly renormalized by a factor of ∼16 compared with LDA calculations, while dxz and dyz bands are only renormalized by factors of ∼4. Moreover, in the FeTe1−xSex family, it has been found that the dxy band renormalization factor strongly increases towards the FeTe end compared with that of dxz/dyz, further revealing the strong orbital dependence in the itinerant to localized crossover in this system33. For KFS, the dxy hole band is renormalized by a factor of ∼10 compared with the factor of ∼3 for dxz/dyz bands19. This is even more apparent in FS/STO, where enhanced dxy orbital matrix elements in the second BZ shows the nearly flat dxy hole band extending towards the bottom of the shallow electron bands at M with a noticeable hybridization gap (Fig. 3b). In contrast, in BFCA, the renormalization factor for dxy hole band is comparable to that of the dxz/dyz hole bands (2∼3) (ref. 2), as can be seen in the band slopes in the second derivative plot (Fig. 1l). In summary, all three FeCh systems show much stronger renormalization in the dxy orbital compared with the dxz/dyz orbitals in the low-temperature state, in contrast to the FePns. Here we would like to note that while ARPES is a surface-sensitive probe, the universal orbital-selective renormalization among the FeChs despite their different structure and surface terminations indicate that these properties must represent the bulk, rather than a result of extrinsic variation of surface properties.
Temperature dependence
Next, by raising temperature sufficiently high, we notice that in all three FeCh systems, the dxy orbital-dominated bands lose spectral weight completely (Fig. 4), as reported previously for KFS19. This can be seen first in the disappearance of the shallow dxy hole band near the Γ point. In the low-temperature state of FTS, the dxy hole band crosses the dyz hole band near Γ, and a small hybridization gap appears as can be seen in the discontinuous intensity pattern of the strong dyz hole band (Fig. 4a). At high temperature, this discontinuity disappears as only the dxz and dyz hole bands remain (Fig. 4d). In KFS, the nearly flat dxy hole band in the low-temperature state is entirely above the dxz/dyz hole band tops (Fig. 4c), and clearly disappears at high temperatures (Fig. 4f). The second evidence for the disappearance of dxy orbital at high temperatures is the vanishing of the apparent gap between the electron band bottom and the dyz hole band top at M. As shown in the schematic (Fig. 4g,h), when the dxy band disappears, its hybridization gap with the dxz electron band naturally vanishes, recovering the deeper non-hybridized dxz electron band whose bottom is degenerate with the dyz hole band top as expected. This is clearly seen in the high-temperature data in all three systems (Fig. 4d–f). Here we note that while KFS is known to have phase separation issues with the existence of superconducting regions and insulating regions19, FTS and FS/STO, on the other hand, do not have such complication. Hence the universal behaviour of vanishing dxy spectral weight with raised temperature observed here reflects an intrinsic effect rather than a result of intricate phase separation in KFS.
(a–c) Second energy derivatives of band structure along the Γ–M cut of FTS, FS/STO and KFS, same as that of Fig. 1i–k, taken in the low-temperature state at 15, 9 and 10 K, respectively. (d–f) Same as that of a–c but taken in the high-temperature state at 120, 190 and 210 K, respectively. (g) Schematic showing the band structure in the low-temperature state with finite spectral weight of dxy orbital (red: dxz, green: dyz and blue: dxy). (h) Schematic showing the band structure in the high-temperature state after dxy orbital completely loses spectral weight.
To examine this temperature dependence more carefully, we have quantitatively analysed the spectral weight of each FeCh system. For FTS, we track the dxy hole band slightly away from the Γ point where it is well separated from the dyz hole band (Fig. 5a). From the energy distribution curve at this momentum, we fit Gaussian peaks for both dxy hole band near EF and dyz hole band at higher energies, along with a Shirley background (Fig. 5d), and track the integrated spectral weight of the dxy and dyz peaks as a function of temperature. Comparing these two orbitals, we see that the dxy spectral weight drops to zero ∼110 K, in contrast to a very weak decrease of the dyz spectral weight. This is very similar to the situation in FS/STO and KFS, where we track the spectral weight of the dxy orbital at the dxy electron band bottom at M. For KFS, the fitted peak area precipitously drops ∼100 K, and approaches zero above 180 K (Fig. 5i). For FS/STO, the dxy spectral weight approaches zero above 150 K while that of the dyz orbital remains finite (Fig. 5h), demonstrating the orbital dependence of this temperature evolution.
(a–c) Raw spectral images of FTS, FS/STO and KFS taken in the low-temperature state. Yellow regions mark the momentum ranges integrated for energy distribution curve (EDC) analysis for each compound. (d) Integrated EDCs in the yellow region of a for FTS at selected temperatures, fitted by a Shirley background (grey), a Gaussian for the dxy band (blue), and a Gaussian for the dyz band (green), convolved by the Fermi–Dirac function. (e) Integrated EDCs in the yellow region of b for FS/STO at selected temperatures, with a Gaussian background (grey), a Gaussian for the dxy band (blue) and a Gaussian for the dyz band (green). (f) Integrated EDCs in the yellow region of c for KFS at selected temperatures, fitted by a Gaussian background (grey), and a Gaussian for the dxy band (blue). Residual spectral weight for the dxy peak is shaded for each temperature for all compounds. Fitted peaks for the lowest temperature are shown for each compound. (g–i) Temperature dependence of the fitted areas of the dxy and dyz peaks for FTS, FS/STO and KFS. Guides to eye are drawn in grey to show the trends. All curves are normalized by the initial value of the peak area. The error bars in g–i are error bars resulted from the fitting.
Theoretical calculations
For all three FeCh superconductors studied, two observations are universal: (i) strong orbital-dependent renormalization at low temperatures and (ii) disappearance of dxy spectral weight with raised temperatures. Theoretically, these behaviours can be understood in proximity to an OSMP, as predicted by both a slave-spin mean-field method34 and dynamical mean-field theory method35 taking into account sufficiently strong intra-orbital Coulomb repulsion U and Hund’s coupling J. These works show that the FeChs are close to an OSMP in which the dxy orbital is completely Mott localized while the other orbitals remain itinerant, and that a temperature scale could be identified where the dxy orbital loses coherence and spectral weight, together with its hybridization to the other orbitals.
The orbital selectivity arises from two factors19,34. The crystal field splitting of the tetragonal lattice makes the dxy orbital energy level higher than that of dxz/dyz. Because the threshold interaction for the Mott transition is larger for degenerate orbitals than for non-degenerate orbitals36, it is easier to localize the dxy electrons. The tendency towards OSMP is further enhanced when the projected bandwidth is different37, as is the case here with the dxy band being narrower than the dxz/dyz bands. When the material is sufficiently close to such an OSMP, the dxy mass renormalization is much stronger than that of other orbitals, as observed in the low-temperature state of the FeChs. For the system to be close to this OSMP, it must exhibit strong electron correlations, which from the two theoretical studies is shown to be a combined result of Coulomb interactions U and Hund’s coupling J.
Among the three FeChs, FTS is undoped, with n=6, while FS/STO and KFS are electron doped, with n=6.12 and 6.15, as estimated from FS volume counting. Figure 6 shows our calculated transition temperatures into the OSMP versus U phase diagrams for systematic dopings from n=6–6.15. The blue shading indicates the dxy quasiparticle spectral weight, Zxy, for each doping. When Zxy drops to zero, the system enters the OSMP. This transition boundary is marked by solid blue lines in Fig. 6. Furthermore, we see that for and only for integer filling, n=6 in the calculated doping range, there exists a Mott insulator phase (marked by a red line), where all orbitals become Mott localized with sufficiently large U. With increasing electron filling, the critical U for the system entering the OSMP at a given temperature shifts to larger values, as can be seen by tracing the blue lines at both 10 and 240 K, indicating that electron doping brings the system away from the OSMP. This is consistent with the observation that the temperature at which the dxy spectral weight disappears increases from FTS (110 K) to the doped FS/STO (150 K) and KFS (180 K). Here we note that the resistivity for the FeTe1−xSex family exhibits a weak hump18 suggestive of a crossover from insulating-like to metallic-like behaviour much like the case of KFS10, and this crossover temperature scale shifts to lower value with decreasing x, consistent with the stronger renormalization values towards the FeTe end33 and the understanding that the low-temperature state of FeTe end sits closer to the OSMP.
Slave-spin mean-field phase diagrams of the five-orbital Hubbard model at systematic electron fillings from n=6–6.15. See Methods for calculation details. Blue shading shows the dxy quasiparticle spectral weight, Zxy. The OSMP phase boundary is shown by solid blue lines connecting blue squares marking the calculated temperatures where Zxy drops to zero. A Mott insulator (MI) phase exists for n=6, where all orbitals have zero spectral weight. Its phase boundary is marked by a red line. The temperatures at which Zxy is observed to vanish in FTS, FS/STO and KFS are marked by magenta dotted lines. From these temperatures, the critical U’s for FTS, FS/STO and KFS can be estimated, which is shown as a yellow guide to the eye strip at fixed U. Hund’s J is fixed at 0.6 eV. Here, electron doping bring the system away from the OSMP, as seen in the increasing critical U at fixed temperature (blue lines at 10 and 240 K) as well as the increasing critical temperature at fixed U (magenta dots).
Discussion
The strong orbital-selective behaviour in the FeCh family is a manifestation of its strong electron correlations, and suggests that they may serve as a bridge between the strongly correlated cuprates as doped Mott insulators and the weaker correlated FePns that are more itinerant. The OSMP of the FeChs can only occur when the overall electron correlations are strong. In that sense, the existence of an OSMP indicates the presence of strong correlations, such that the system is in proximity to a Mott transition. The latter links these materials to the cuprates, where optimal superconductivity develops not too far from a Mott insulating state. The linkage can be made more explicit by the Hund’s coupling-induced suppression of the interorbital coupling in the case of the iron-based materials19,34,38. This is relevant to the current discussion on the pairing mechanism of FeSC in both KFS and FS/STO as the lack of hole pockets do not seem to prevent them from superconducting at temperatures comparable to or even higher than FePns, which is unexpected from a weak-coupling FS nesting picture3. In a recent theoretical study39, it has been shown that under a strong coupling approach, where the driving force for pairing comes from the close-neighbour exchange interactions, the pairing strength can be comparable in the FeChs and FePns, as they approach a Mott transition by increasing exchange interaction in the former and reducing the renormalized bandwidth in the latter. The observed universal strong correlation in the FeChs and proximity to an OSMP here supports such a scenario.
Methods
Sample growth
High-quality single crystals of K0.76Fe1.72Se2 and FeTe0.56Se0.44 were grown using the flux method19,40. Monolayer FeSe films were grown on SrTiO3 using molecular beam epitaxy17.
ARPES measurements
ARPES measurements were carried out at beamline 5-4 of the Stanford Synchrotron Radiation Lightsource and beamline 10.0.1 of the Advanced Light Source using SCIENTA R4000 electron analyzers. The total energy resolution was set to 10 meV and the angular resolution was 0.3°. Single crystals were cleaved in situ at 10 K for each measurement. The FeSe films were transported to the beamline under vacuum and further annealed before measurements. All measurements were done in ultra high vacuum with a base pressure lower than 4 × 10−11 torr.
Theoretical calculations
The theoretical calculations were done using a slave-spin mean-field method on a five-orbital Hubbard model34, with tight-binding parameters for FTS. Hund’s J is fixed at 0.6 eV.
Additional information
How to cite this article: Yi, M. et al. Observation of universal strong orbital-dependent correlation effects in iron chalcogenides. Nat. Commun. 6:7777 doi: 10.1038/ncomms8777 (2015).
References
Lu, D. H. et al. Electronic structure of the iron-based superconductor LaOFeP. Nature 455, 81–84 (2008).
Yi, M. et al. Electronic structure of the BaFe2As2 family of iron-pnictide superconductors. Phys. Rev. B 80, 024515 (2009).
Mazin, I. I., Singh, D. J., Johannes, M. D. & Du, M. H. Unconventional Superconductivity with a sign reversal in the order parameter of LaFeAsO1−xFx . Phys. Rev. Lett. 101, 057003 (2008).
Si, Q. & Abrahams, E. Strong correlations and magnetic frustration in the high TC iron pnictides. Phys. Rev. Lett. 101, 076401 (2008).
Yu, R., Zhu, J.-X. & Si, Q. Mott transition in modulated lattices and parent insulator of (K,Tl)yFexSe2 superconductors. Phys. Rev. Lett. 106, 186401 (2011).
Yin, Z. P., Haule, K. & Kotliar, G. Kinetic frustration and the nature of the magnetic and paramagnetic states in iron pnictides and iron chalcogenides. Nat. Mater. 10, 932–935 (2011).
Qazilbash, M. M. et al. Electronic correlations in the iron pnictides. Nat. Phys. 5, 647–650 (2009).
Liu, M. et al. Nature of magnetic excitations in superconducting BaFe1.9Ni0.1As2 . Nat. Phys. 8, 376–381 (2012).
Hsu, F.-C. et al. Superconductivity in the PbO-type structure α-FeSe. Proc. Natl Acad. Sci. 105, 14262–14264 (2008).
Guo, J. et al. Superconductivity in the iron selenide KxFe2Se2 (0≤x≤1.0). Phys. Rev. B 82, 180520 (2010).
Wang, Q. Y. et al. Interface induced high temperature superconductivity in single unit-cell FeSe films on SrTiO3 . Chin. Phys. Lett. 29, 037402 (2012).
Bao, W. et al. A novel large moment antiferromagnetic order in K0.8Fe1.6Se2 superconductor. Chin. Phys. Lett. 28, 086104 (2011).
Fang, M.-H. et al. Fe-based superconductivity with TC=31K bordering an antiferromagnetic insulator in (Tl,K)FexSe2 . Europhys. Lett. 94, 27009 (2011).
Zhang, Y. et al. Nodeless superconducting gap in AxFe2Se2 (A=K,Cs) revealed by angle-resolved photoemission spectroscopy. Nat. Mater. 10, 273–277 (2011).
Qian, T. et al. Absence of a holelike fermi surface for the iron-based K0.8Fe1.7Se2 superconductor revealed by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 106, 187001 (2011).
Liu, D. et al. Electronic origin of high-temperature superconductivity in single-layer FeSe superconductor. Nat. Commun. 3, 931 (2012).
Lee, J. J. et al. Interfacial mode-coupling as the origin of the enhancement of TC in FeSe films on SrTiO3 . Nature 515, 245–248 (2014).
Liu, T. J. et al. From (π,0) magnetic order to superconductivity with (π,π) magnetic resonance in Fe1.02Te1−xSex . Nat. Mater. 9, 718–720 (2010).
Yi, M. et al. Observation of temperature-induced crossover to an orbital-selective Mott phase in AxFe2−ySe2 (A=K,Rb) superconductors. Phys. Rev. Lett. 110, 067003 (2013).
Wang, Z. et al. Orbital-selective metal-insulator transition and gap formation above TC in superconducting Rb1−xFe2−ySe2 . Nat. Commun. 5, 3202 (2014).
Ding, X. et al. Strong and nonmonotonic temperature dependence of Hall coefficient in superconducting KxFe2−ySe2 single crystals. Phys. Rev. B 89, 224515 (2014).
Li, W. et al. Mott behaviour in KxFe2−ySe2 superconductors studied by pump-probe spectroscopy. Phys. Rev. B 89, 134515 (2014).
Yi, M. et al. Symmetry-breaking orbital anisotropy observed for detwinned Ba(Fe1−xCox)2As2 above the spin density wave transition. Proc. Natl Acad. Sci. USA 108, 6878–6883 (2011).
Yi, M. et al. Electronic reconstruction through the structural and magnetic transition in detwinned NaFeAs. New J. Phys. 14, 073019 (2012).
Zhang, Y. et al. Symmetry breaking via orbital-dependent reconstruction of electronic structure in uniaxially strained NaFeAs. Phys. Rev. B 85, 085121 (2012).
Nakayama, K. et al. Reconstruction of band structure induced by electronic nematicity in FeSe superconductor. Phys. Rev. Lett. 113, 237001 (2014).
Shimojima, T. et al. Lifting of xz/yz orbital degeneracy at the structural transition in detwinned FeSe. Phys. Rev. B 90, 121111(R) (2014).
Watson, M. D. et al. Emergence of the nematic electronic state in FeSe. Phys. Rev. B 91, 155106 (2015).
Zhang, P. et al. Evidence for intertwining orders in the electronic nematic state of FeSe. Preprint at http://arxiv.org/abs/1503.01390 (2015).
Tan, S. et al. Interface-induced superconductivity and strain-dependent spin density waves in FeSe/SrTiO3 thin films. Nat. Mater. 12, 634–640 (2013).
Zhang, Y. et al. Distinctive momentum dependence of the band reconstruction in the nematic state of FeSe thin film. Preprint at http://arxiv.org/abs/1503.01556 (2015).
Lee, P. A. & Wen, X.-G. Spin-triplet p-wave pairing in a three-orbital model for iron pnictide superconductors. Phys. Rev. B 78, 144517 (2008).
Liu, Z. K. et al. Experimental observation of incoherent-coherent crossover and orbital dependent band renormalization in iron chalcogenide superconductors. Preprint at http://arxiv.org/abs/1505.03074 (2015).
Yu, R. & Si, Q. Orbital-selective Mott phase in multiorbital models for alkaline iron selenides K1−xFe2−ySe2 . Phys. Rev. Lett. 110, 146402 (2013).
Yin, Z. P., Haule, K. & Kotliar, G. Fractional power-law behaviour and its origin in iron-chalcogneide and ruthenate superconductors: insights from first-principles calculations. Phys. Rev. B 86, 195141 (2012).
de’ Medici, L., Hassan, S. R., Capone, M. & Dai, X. Orbital-selective Mott transition out of band degeneracy lifting. Phys. Rev. Lett. 102, 126401 (2009).
Anisimov, V., Nekrasov, I. A., Kondakov, D. E., Rice, T. M. & Sigrist, M. Orbital-selective Mott-insulator transition in Ca2−xSrxRuO4 . Eur. Phys. J. B 25, 191 (2002).
de’ Medici, L., Giovannetti, G. & Capone, M. Selective Mott physics as a key to iron superconductors. Phys. Rev. Lett. 112, 177001 (2014).
Yu, R., Goswami, P., Si, Q., Nikolic, P. & Zhu, J.-X. Superconductivity at the border of electron localization and itinerancy. Nat. Commun. 4, 2783 (2013).
Liu, T. J. et al. Charge-carrier localization induced by excess Fe in the superconductor Fe1+yTe1−xSex . Phys. Rev. B 80, 174509 (2009).
Nekrasov, I. A. & Sadovskii, M. V. Electroni structure, topological phase transitions and superconductivity in (K, Cs)xFe2Se2 . JETP Lett. 93, 166–169 (2011).
Acknowledgements
ARPES experiments were performed at the Stanford Synchrotron Radiation Lightsource and the Advanced Light Source, which are both operated by the Office of Basic Energy Sciences, U.S. Department of Energy. The Stanford work is supported by the US DOE, Office of Basic Energy Science, Division of Materials Science and Engineering, under award number DE-AC02-76SF00515. The work at Rice is supported by NSF Grant DMR-1309531 and the Robert A. Welch Foundation Grant No. C-1411. The work at Renmin University is supported by the National Science Foundation of China Grant number 11374361, and the Fundamental Research Funds for the Central Universities and the Research Funds of Remnin University of China. The work at Tulane is supported by the NSF under grant DMR-1205469. The work at Los Alamos was supported by the U.S. DOE Office of Basic Energy Sciences.
Author information
Authors and Affiliations
Contributions
M.Y., Z.K.L. and Y.Z. performed the ARPES experiments with assistance from M.H. and S.K.M. under the guidance of D.H.L. and Z.H. R.Y., J.X.Z. and Q.S. performed the theoretical calculations. J.J.L., R.G.M., F.T.S. and W.L. grew the FeSe films. S.C.R., J.H.C. and B.L. grew the KFS single crystals with guidance from I.R.F. and C.W.C. J.H. grew the FTS single crystals under the guidance of Z.Q.M. Z.X.S. and D.H.L. provided overall guidance and project coordination. The paper was written by M.Y., D.H.L., R.Y. and Q.S. with contributions from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Yi, M., Liu, ZK., Zhang, Y. et al. Observation of universal strong orbital-dependent correlation effects in iron chalcogenides. Nat Commun 6, 7777 (2015). https://doi.org/10.1038/ncomms8777
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms8777
This article is cited by
-
Non-Fermi liquid behaviour in a correlated flat-band pyrochlore lattice
Nature Physics (2024)
-
Kondo interaction in FeTe and its potential role in the magnetic order
Nature Communications (2023)
-
Nematic fluctuations in an orbital selective superconductor Fe1+yTe1−xSex
Communications Physics (2023)
-
Resurgence of superconductivity and the role of dxy hole band in FeSe1−xTex
Communications Physics (2023)
-
Atomic construction and spectroscopic characterization of FeSe-derived thin films on SrTiO3 substrates
AAPPS Bulletin (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.