Abstract
In contrast to a complex feature of antinodal state, suffering from competing orders, the pairing gap of cuprates is obtained in the nodal region, which therefore holds the key to the superconducting mechanism. One of the biggest question is whether the point nodal state as a hallmark of d-wave pairing collapses at Tc like the BCS-type superconductors, or it instead survives above Tc turning into the preformed pair state. A difficulty in this issue comes from the small magnitude of the nodal gap, which has been preventing experimentalists from solving it. Here we use a laser ARPES capable of ultrahigh-energy resolution, and detect the point nodes surviving far beyond Tc in Bi2212. By tracking the temperature evolution of spectra, we reveal that the superconductivity occurs when the pair-breaking rate is suppressed smaller than the single-particle scattering rate on cooling, which governs the value of Tc in cuprates.
Similar content being viewed by others
Introduction
In cuprates, the energy gap (pseudogap) starts opening at a temperature much higher than Tc, in some cases above room temperature. Many experimental evidences1,2,3,4,5,6,7,8,9 point to a competing-order origin, rather than the preformed pair, for the pseudogap observed around the antinode with the maximum energy gap. The pseudogap state has been revealed to sharply diminishes toward the antinode and disappear far off the node by the spectral weight analysis for the angle-resolved photoemission spectroscopy (ARPES) data of optimally doped samples9. This is compatible with the recent results by the scanning tunnelling spectroscopy (STM) and the resonant X-ray scattering, showing that the density wave Q-vectors are detected only in the Cu–O bond directions5,7,10,11,12. While the whole Fermi surface is eventually dominated by the pseudogap close to the Mott insulating phase6,13,14, the ‘pure’ pairing state seems to be realized around the node at least in the optimally and overdoped regime9,15,16,17,18,19,20,21. The relevant feature to it would be the spatially homogeneous electronic state seen at the low bias in the STM spectra, which reflects the nodal momentum region11,20,22. It strongly contrasts to the highly inhomogeneous spectra at the high bias associated with the antinodal states. Unveiling the nature of the spectral gap near the node is therefore crucial to elucidate the superconducting mechanism in cuprates. A difficulty however is the small magnitude of the gap, which has been challenging the experimentalists to investigate.
It has been proposed that the pairing-gap evolution with temperature simply follows the conventional Bardeen-Cooper-Schrieffer (BCS) function15, and Fermi arcs (disconnected segments of gapless Fermi surface)23 emerge at Tc6,15,16,17,20,21,22,23,24, marking momentum borders between the superconducting and the competing pseudogap regions6,15. However, it seems contradicting the observations of the Nernst and diamagnetic effects above Tc25,26, which are viewed as signatures of a phase-incoherent superconductivity.
Recently, a contrasting view was proposed9,18,19: its underlying idea is that one should discard the notion of electron quasiparticles, instead pay attention to the density of states, which is an effective way of judging the existence of energy gap. Accordingly, a momentum integration of ARPES spectra has been performed over a selected part of the momentum space. This quantity contributed from the nodal region was found to have a gap-like structure even above Tc18,19. The result seems to be in direct opposition to the above widely accepted view. Nevertheless, the evidence for single-particle gap with the point nodes surviving above Tc is still missing, and strongly desired to unveil the nature of Fermi arc, which is tied to the pairing mechanism of cuprates.
The determination of the momentum-resolved gap structure has been also attempted by STM studies through the spectral line-shape analysis20 and by applying the octet model to the interference pattern21,27,28. While these STM techniques are very successful, they seem to be limited to the investigation of the antinodal region; the gap structure close to the node is not determined27,28, or the gapless Fermi arc is obtained even below Tc20,21, which has never been reported by the ARPES studies. It is thus crucial to investigate the nodal region by means of the ARPES, which is specialized for an observation of the momentum space.
Here we examine the momentum-resolved single-particle spectra of Bi2212 obtained by a laser ARPES29. The ultrahigh-energy resolution and bulk sensitivity achieved by utilizing a low-energy laser source (hν=7 eV) enabled us to obtain high-quality spectra with an extremely sharp line shape. We demonstrate, within the quasiparticle picture, the absence of the gapless Fermi arc at Tc, and an isotropic temperature evolution of point nodal pairing state persistent far above Tc. We find that not only the single-particle scattering rate (Γsingle), but also the pair-breaking rate (Γpair) is required to reproduce the ARPES spectra. Furthermore, the magnitude of Tc is determined by the mutual relation between Γsingle and Γpair in the form of Γsingle(Tc)=Γpair(Tc). Importantly, the momentum-integrated spectra of ARPES and STM previously investigated are not capable of separating these two quantities (Γsingle and Γpair) (see Supplementary Note 4); thus, the present results provide novel ingredients essential to formulate the pairing mechanism of cuperates.
Results
Absence of Fermi arc at Tc
In Fig. 1, we show typical data obtained inside the nodal region where the Fermi arc (bold orange curve in the inset of Fig. 1d) was previously claimed to appear at Tc6,15,16,20,24. The ARPES intensity map divided by the Fermi function (see Fig. 1a) shows an energy gap and an upper branch of the Bogoliubov dispersion at low temperatures, as an indication of the pairing state. We extract the spectra at the Fermi momentum (kF) over a wide range of temperature in Fig. 1b, and plot the peak energies (ɛpeak) in Fig. 1e. In the same panel, we also plot ɛpeak of energy distribution curves (EDCs) symmetrized about the Fermi energy (EF) to remove the effect of Fermi cutoff23, and confirm a consistency between the two different methods. Our high-quality data clearly exhibit that the gap is open even at Tc (=92 K) (see green spectra in Fig. 1b,c), and the ɛpeak(T) disagrees with the BCS gap evolution (blue solid curve in Fig. 1e). Even if assuming a phase fluctuation slightly above Tc, the BCS-type curve (blue dashed curve) still does not fit to the data.
(a) Dispersion maps at several temperatures measured along a momentum cut close to the node in OP92K (a red line in the inset of d). Each map is divided by the Fermi function at the measured temperature. (b) Temperate evolution of EDCs at kF (a circle in the inset of d) from deep below (10 K) to much higher than Tc (130 K). Each spectrum is divided by the Fermi function at the measured temperature. (c) The same data as in b, but symmetrized about EF. (d) The same data as in c plotted without an offset. The inset represents the Fermi surface. The bold orange line indicates the momentum region where the Fermi arc was previously claimed to emerge at Tc. (e) Peak energies of spectra in b and c plotted as a function of temperature, ɛpeak. The solid and dashed blue curves show the BCS gap function with an onset at Tc (92 K) and slightly above Tc, respectively. Error bars in e represent standard deviations of the spectral peak positions.
To pin down the cause of this anomaly, we examine the momentum variation of ɛpeak(T) for the optimally and overdoped samples (OP92K and OD72K) in Fig. 2a,b, respectively. Surprisingly, the gap does not close at Tc regardless of kF points. The symmetrized EDCs around the node for OP92K are plotted in Fig. 3b (T=10 K) and Fig. 3c (T=Tc). We find that the d-wave gap with a point node persists at Tc (Fig. 3d); the Fermi arc is absent. While a small uncertainty in gap estimation remains in the close vicinity of the node due to the finite spectral width, it is negligible compared with the previously reported extensive gapless Fermi arc (orange arrows in the inset of Fig. 2a,b). The absence of Fermi arc is further confirmed in Fermi function divided band dispersions (Fig. 3a) measured at Tc along several momentum cuts (colour lines in the inset of Fig. 3d). The loss of spectral weight at EF due to the gap opening is seen in all the maps except for at the node (see Supplementary Fig. 6 for more details). Our high-resolution data also show other inconsistencies with the previous expectations6,15,16,17. First, the length of arc with single spectral peaks (ɛpeak=0) is not linearly extrapolated to zero at T=0 against the nodal liquid behaviour (Supplementary Fig. 7)16,17. Second, the temperature evolution of such an arc is gradual up to far above Tc with no indication of momentum borders separating two distinct states6,15.
(a,b) Temperature dependence of spectral peak energy, ɛpeak(T), at various kF points (colour circles in the insets) for OP92K and OD72K, respectively. In the bottom of each panel, the same curves of ɛpeak(T) are normalized to the maximum value at the lowest temperature. A red dashed curve and a green solid curve are the BCS gap function with the onset at Tc and Tpair, respectively (Tpair=135 K for OP92K and Tpair=89 K for OD89K). The inset shows the Fermi surface with measured kF points (colour circles). The bold orange line indicates the momentum region where the Fermi arc was previously claimed to emerge at Tc. Error bars in a and b represent standard deviations of the spectral peak positions.
(a) Dispersion maps at Tc along several momentum cuts (colour lines in the inset of d measured for OP92K. Each map is divided by the Fermi function at the measured temperature. The described φ are the directions of measured kF points (φ is defined in the inset of d). (b,c) Symmetrized EDCs at kF over a wide range of angle φ (colour circles in the inset of d) at 10 K and Tc (=92 K), respectively. The red dotted lines are guide to the eyes for the gap evolution. (d) Fermi angle φ dependence of peak energies of spectra in b (ɛpeak(10 K)) and c (ɛpeak(Tc)). The orange arrows indicate the momentum region where the Fermi arc was previously claimed to emerge at Tc.
For a further examination, we normalize each curve of ɛpeak(T) to the maximum value at the lowest temperature in the bottom panels of Fig. 2a (OP92K) and 2b (OD72K). One can confirm that the data are mismatched with the conventional BCS curve (red dashed curves) even in the close vicinity of the node. More importantly, the ɛpeak(T) behaviour with a steep drop to zero becomes more gradual with getting away from the node, and it eventually follows a BCS-type gap function (green curves) with an onset much higher than Tc (∼135 K and ∼89 K for OP92K and OD72K, respectively).
Point nodal gap above Tc by the leading edge shift
To clarify the anomalous feature above Tc, here we investigate another spectral measure, so-called leading edge of EDC, which is also commonly used for a gap estimation. Figure 4a–d shows the non-symmetrized EDCs of OP92K, normalized to the peak intensity of each curve. The energy location of spectral leading edge (ɛLE), at which the spectral intensity becomes half (allows in a–d), is plotted in Fig. 4e–h as a function of temperature. The nodal values (Fig. 4e) have a T-linear behaviour, which is expected for the spectra dominated by the Fermi cutoff effect. While the nodal ɛLE(T) could have a complex behaviour30 with a poor energy resolution, such a effect seems not to be observed in our case. Hence, even the slightest energy gap could be detected as the deviation of ɛLE(T) from the T-linear behaviour. Such a deviation is indeed observed for all the k points off the node (Fig. 4f–h). It is more clearly demonstrated in the bottom panels of Fig. 4f–h, where the difference of ɛLE(T) from the T-linear behaviour is extracted. An astonishing result we found is that the onset temperatures are almost the same (∼135 K) regardless of the directions (φ), which validates that the point nodal state persists up to ∼135 K.
(a) The temperature evolution of ARPES spectra (EDCs) at the gap node for OP92K, normalized to the peak intensity of each curve. (b–d) The same spectra as a, but measured off the node (colour circles in the inset of e). (e–h) Temperature dependence of the spectral leading edge, ɛLE(T), defined as energies where the spectral peaks become half in intensity (marked by arrows in a–d). The bottom panels of f–h plot the difference of ɛLE(T) from the T-linear behaviours (red dashed lines), which are fit to ɛLE(T) at high temperatures. The onset temperatures of the deviation from T-linear behaviour are around 135 K for all the kF points off the node (dashed circles). A kink is seen in the difference curve for f (small black arrow) because the thermally populated Bogoliubov peaks in the unoccupied side significantly affect the shapes of leading edge specially at kFs close to the node with small gaps. The inset of e shows the Fermi surface with the examined kF points. The bold orange arrow indicates the momentum region where the Fermi arc was previously claimed to emerge at Tc.
Importantly, the gap opening temperature is coincident with the onset of the BCS-type gap function obtained with the symmetrized EDCs far off the node (a green curve in Fig. 2a). A plausible explanation for it is that the spectral peak energy underestimates the ‘real’ energy gap (ɛpeak<Δ)9,31,32, and energy gaps (Δ) comparable to or smaller than the peak width cannot be detected by tracing the peak positions (see a simulation in the Supplementary Fig. 8). This situation could occur at high temperatures, and it gets more serious towards the node with smaller Δ. We actually detect the signature of such a small gap in the off-nodal spectra with a single peak above Tc (Supplementary Fig. 10); the spectral width becomes smaller with increasing temperature up to ∼135 K, which contrasts to the monotonic broadening seen in the nodal direction. The characteristic momentum variation of ɛpeak(T) in Fig. 2a,b, therefore, could be a natural consequence of Δ(T) having the same onset temperature at ∼135 K and ∼89 K, respectively, for all directions (φ).
Anomalous pair formation in cuprates
We find below that a model spectral function, πA(kF, ω)=Σ′′/[(ω−Σ′)2+Σ′′2], with such a BCS-type Δ(T, φ) indeed reproduces the ARPES spectra, whereas the traditionally used assumption of Δ(T, φ)≡ɛpeak(T, φ) is invalid. The self-energy (Σ=Σ′+iΣ′′) we use has a minimal representation with two different scattering rates, Γ0 and Γ1 (refs 32, 33),

Here Γ1 is a single-particle scattering rate and it causes the broadening of a peak width. On the other hand, Γ0 fills the spectral weight around EF, and should be viewed as the inverse pair lifetime (or pair-breaking rate). For clarity, we label the former Γsingle and the latter Γpair in the rest of this paper. We emphasize that the intensity at EF in a gapped spectrum becomes non-zero only when Γpair≠0 as simulated in Supplementary Fig. 8a. Our spectra measured at the low temperatures (T≪Tc) have a negligible intensity at EF, which ensures that our data are almost free from impurity-causing pair-breaking effect. At elevated temperatures, we observe a remarkable gap filling (see Fig. 1d and Supplementary Figs 2 and 5). Significantly, it actually begins from deep below Tc, which is not expected in a conventional BCS superconductor. Since the data were measured at the extremely high energy resolution (Δɛ=1.4 meV), we can rule out the possibility, assumed before with setting Γpair≡0 (refs 6, 15), that the filling is caused by a spectral broadening due to the experimental energy resolution. The intensity at EF should instead be a signature of intrinsic pair breaking; hence, it must be taken into account for the gap estimation. In passing, we note that the Γsingle and Γpair both equally increase the intensity around EF of the momentum-integrated spectrum previously studied by ARPES9,18,19 and STM20,34 (see Supplementary Fig. 9), which is therefore incapable of disentangling these two different scattering rates.
Following this consideration, we set Γsingle (or Γ1) and Γpair (or Γ0) to be independent free parameters in equation (1). First, we performed a spectral fitting to our ARPES data, assuming Δ(T)≡ɛpeak(T), which is a traditional way of gap estimation (Supplementary Figs 11a and 12a). The obtained parameter of Γsingle(T) (middle panel of Supplementary Figs 11a and 12a) is strongly deviated from a monotonic decrease on cooling, having an unrealistic upturn around the temperature at which the ɛpeak becomes zero. As already discussed above, this anomaly is expected when the spectrum with a single peak (ɛpeak=0) has an energy gap (Δ≠0); thus, the spectral width overestimates the scattering rate.
We find that this circumstance is corrected by applying a BCS-type gap function with an onset at 135 and 89 K for OP92K and OD72K (green curves in the bottom panels of Fig. 2a,b), respectively, regardless of the Fermi angle φ. In the Supplementary Figs 14 and 15, we fit equation (1) with such a gap function Δ to our ARPES data near the node measured over a wide temperature range. As an example, the result at φ=13.5° for OP92K is shown in Fig. 5c. The fitting curves (red curves) almost perfectly reproduce the data (black curves). The obtained Γsingle(T) (Fig. 5a,b) in the gapped region agree with Γsingle(T) at the node, which can be determined simply from the spectral width. Similarly, the Γpair(T) curves are also almost identical for all the φ. The consistency in our results pointing to the isotropic scattering mechanism validates our model spectral function characterized by the BCS-type Δ(T, φ). The famous ‘hot spots’, at which the scattering rate is abruptly enhanced, should be situated at much higher φ (Supplementary Fig. 13). The applied onset temperatures are almost the same as those of Nernst and diamagnetic effects25,26, which are viewed as signatures of phase-incoherent superconductivity. The comparable temperatures are also obtained by the specific heat measurements35 and the other spectroscopic techniques36,37. Therefore, we assign ∼135 and ∼89 K to be the onset temperature of pair formation (Tpair) of OP92K and OD72K, respectively. This is further supported by the signature of pairing seen in the behaviour of Γsingle(T) (Fig. 5a,b; Supplementary Fig. 16); the decrease of its value on cooling is accelerated across Tpair, showing a deviation from the linear behaviour38. The different experimental techniques could have different sensitivities to the superconducting fluctuation above Tc, and actually the terahertz spectroscopy estimates a slightly lower temperature scale (10–15 K above Tc)39,40. Nonetheless, we stress that the view that the point nodal pairing survives above Tc is compatible in these observations. The doping variation of Tpair/Tc (1.47 and 1.24 for OP92K and OD72K, respectively) obtained in our studies is consistent with the phase-fluctuating superconductivity, which merges to the superconducting dome with heavily overdoping41. The competing ordered phase is, in contrast, claimed to terminate at zero temperature inside the superconducting dome42, thus, disagrees with the present gapped states observed above Tc even in the overdoped sample.
(a) The BCS-type gap function used for the fitting to the OP92K data (a green curve), and the obtained single-particle scattering rate (Γsingle, or Γ1) and the pair-breaking rate (Γpair, or Γ0) in equation (1). (b) The fitting results same as in a, but for the OD72K data. The values of Γpair at high temperatures are not plotted, since the spectral shape is insensitive to the Γpair when Δ is small or zero, and thus it is impossible to determine the value. A small hump seen in the Γpair around 75 K for φ=11.7° and 13.5° in a comes from a slight difficulty of fitting to the spectra with a peak-dip-hump shape due to the mode coupling, which appears below Tc and gets pronounced with approaching the antinode. Magenta circle marks the crossing point of Γsingle(T) and Γpair(T). Large blue arrow indicates the temperature, at which the Γsingle(T) deviates from a T-linear behaviour on cooling. (c) ARPES spectra (black curves) and fitting results (red curves) providing the parameters for φ=13.5° in a. Error bars in a and b represent standard deviations in fitting the model spectral function to the ARPES spectra.
A simple formula determining the magnitude of Tc in cuprates
The relationship between Γpair and Γsingle should provide rich information relevant for the pairing mechanism. Intriguingly, the superconductivity occurs when the magnitude of Γpair is reduced smaller than that of Γsingle; the Tc is coincident with the temperature at which Γsingle(T) and Γpair(T) crosses (magenta circles in Fig. 5a,b), which provides a simple formula of Γsingle(Tc)=Γpair(Tc). The magnitude of Tpair is reported to be comparable (120∼150 K) among different cuprate families with significantly different Tcs36. The Γsingle(T) also seems to be less sensitive to the different compounds43,44. Therefore, the pair-breaking effect, which controls the fulfillment of Γpair<Γsingle, is predicted to be a critical factor determining the Tc value of cuprates. Notably, a remarkable difference in filling behaviours of the spectral gap is indeed observed between Bi2212 and Bi2Sr2CuO6+δ with about three times different Tcs9,36.
Discussion
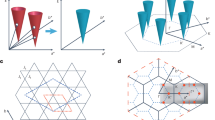
We summarize our conclusion in Fig. 6 by drawing a schematic temperature evolution of the pairing gap. As demonstrated elsewhere9, the pseudogap competing with the pairing disappears far off the node (blue area). In this article, we have investigated the nodal region of optimally and overdosed samples. We revealed that the point node state persists up to far above Tc, against the previous expectation15,16,17,20,21,24, following the BCS-type gap function with the onset at Tpair (∼1.5Tc in the optimal doping). The ARPRS spectra are reproduced by the spectral function with a minimal model, which has a single energy gap all the way up to the gap closing temperature. It is consistent with the expected ‘pure’ pairing state with no contamination by the pseudogap around the node at least in the optimally and overdosed regions. While the gap evolution with an onset at Tpair might be reminiscent of a phase-transition phenomenon, it is against a gradual temperature variation of the specific heat35. The crossover-like behaviours in cuprates should come from the significant pair-breaking effect, which is markedly enhanced above Tc. To fully understand the present results, insight of the spacially inhomogeneous state45 would be essential. However, only that cannot explain our data, since the local density of states itself has the behaviour of gap filling at EF with temperature34. The competing nature of pseudogap state evolving around the antinode1,3 is a plausible source for the unique scattering mechanism, which strongly suppress Tc from Tpair. To evaluate this speculation, however, the more detailed theoretical inputs are required.
(a) Temperature variation of the point nodal d-wave pairing gap. The energy gap has a BCS-type function (inset curve) with the same onset at Tpair regardless of directions (φ) along the Fermi surface. Temperatures for each curve are indicated in the inset with coloured circles. The gapped Fermi surface with a point node below Tc (b) persists beyond Tc (c) up to the temperature of pair formation (Tpair). (d) Emergence of the gapless Fermi arc centered at the node due to the pseudogap evolution around the antinode9,27; while the antinodal region is not observable at the low photon energies like 7 eV, the studies with higher energy photons have demonstrated that the competing pseudogap state emerges at |φ|>25° in the optimal doping9.
Methods
Samples
Optimally doped Bi2Sr2CaCu2O8+δ (OP92 K) and overdoped (Bi,Pb)2Sr2CaCu2O8+δ (OD72 K) single crystals with Tc=92 and 72 K, respectively, were grown by the conventional floating-zone technique. A sharp superconducting transition width of ∼1 K (OP92K) and ∼3 K (OD72K) were confirmed (see Supplementary Fig. 1).
ARPES experiments
ARPES data were accumulated using a laboratory-based system consisting of a Scienta R4000 electron analyser and a 6.994 eV laser. The overall energy resolution in the ARPES experiment was set to 1.4 meV for all the measurements. To accomplish the temperature scan of spectra at a high precision, we applied a technique of the local sample heating, which thermally isolates the sample holder with a heat switch from the lest of the system at elevated temperatures. It minimizes the degassing, allowing us to keep the chamber pressure better than 2 × 10−11 torr during the entire temperature sweeping; no sample aging was confirmed (Supplementary Fig. 4). This method also prevents the thermal expansion of sample manipulator, and it enables us to take data in fine temperature steps with automated measurement of temperature scan from precisely the same spot on the crystal surface, which was essential to achieve the aim of the present study.
Additional information
How to cite this article: Kondo, T. et al. Point nodes persisting far beyond Tc in Bi2212. Nat. Commun. 6:7699 doi: 10.1038/ncomms8699 (2015).
References
Kondo, T., Khasanov, R., Takeuchi, T., Schmalian, J. & Kaminski, A. Competition between the pseudogap and superconductivity in the high-T c copper oxides. Nature 457, 296–300 (2009).
Khasanov, R. et al. Evidence for a competition between the superconducting state and the pseudogap state of (BiPb)2(SrLa)2CuO6+δ from muon spin rotation experiments. Phys. Rev. Lett. 101, 227002 (2008).
Chang, J. et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67 . Nat. Phys. 8, 871–876 (2012).
Hashimoto, M. et al. Particle-hole symmetry breaking in the pseudogap state of Bi2201. Nat. Phys. 6, 414–418 (2010).
Wise, W. D. et al. Charge-density-wave origin of cuprate checkerboard visualized by scanning tunnelling microscopy. Nat. Phys. 4, 696–699 (2008).
Vishik, I. M. et al. Phase competition in trisected superconducting dome. Proc. Natl Acad. Sci. USA 109, 18332–18337 (2012).
Parker, C. V. et al. Fluctuating stripes at the onset of the pseudogap in the high-T c superconductor Bi2Sr2CaCu2O8+δ . Nature 468, 677–680 (2010).
He, R.-H. et al. From a single-band metal to a high-temperature superconductor via two thermal phase transitions. Science 331, 1579–1583 (2011).
Kondo, T. et al. Formation of gapless fermi arcs and fingerprints of order in the pseudogap state of cuprate superconductors. Phys. Rev. Lett. 111, 157003 (2013).
Comin, R. et al. Charge order driven by Fermi-arc instability in Bi2Sr2−xLaxCuO6+δ . Science 343, 390–392 (2014).
McElroy, K. et al. Coincidence of checkerboard charge order and antinodal state decoherence in strongly underdoped superconducting Bi2Sr2CaCu2O8+δ . Phys. Rev. Lett. 94, 197005 (2005).
da Silva Neto, E. H. et al. Ubiquitous interplay between charge ordering and high-temperature superconductivity in cuprates. Science 343, 393–396 (2014).
Razzoli, E. et al. Evolution from a nodeless gap to -wave in underdoped La2−xSrxCuO4 . Phys. Rev. Lett. 110, 047004 (2013).
Peng, Y. et al. Disappearance of nodal gap across the insulator–superconductor transition in a copper-oxide superconductor. Nat. Commun. 4, 2459 (2013).
Lee, W. S. et al. Abrupt onset of a second energy gap at the superconducting transition of underdoped Bi2212. Nature 450, 81–84 (2007).
Kanigel, A. et al. Evolution of the pseudogap from Fermi arcs to the nodal liquid. Nat. Phys. 2, 447–451 (2006).
Nakayama, K. et al. Evolution of a Pairing-Induced Pseudogap from the Superconducting Gap of (Bi,Pb)2Sr2CuO6 . Phys. Rev. Lett. 102, 227006 (2009).
Reber, T. J. et al. The origin and non-quasiparticle nature of Fermi arcs in Bi2Sr2CaCu2O8+δ . Nat. Phys. 8, 606–610 (2012).
Reber, T. J. et al. Prepairing and the ‘filling’ gap in the cuprates from the tomographic density of states. Phys. Rev. B 87, 060506 (2013).
Pushp, A. et al. Extending universal nodal excitations optimizes superconductivity in Bi2Sr2CaCu2O8+δ . Science 324, 1689–1693 (2009).
Lee, J. et al. Spectroscopic fingerprint of phase-incoherent superconductivity in the underdoped Bi2Sr2CaCu2O8+δ . Science 325, 1099–1103 (2009).
Boyer, M. et al. Imaging the two gaps of the high-temperature superconductor Bi2Sr2CuO6+x . Nat. Phys. 3, 802–806 (2007).
Norman, M. R. et al. Destruction of the Fermi surface in underdoped high-T c superconductors. Nature 392, 157–160 (1998).
Kanigel, A. et al. Protected nodes and the collapse of fermi arcs in high-T c cuprate superconductors. Phys. Rev. Lett. 99, 157001 (2007).
Wang, Y., Li, L. & Ong, N. Nernst effect in high-T c superconductors. Phys. Rev. B 73, 024510 (2006).
Wang, Y. et al. Field-enhanced diamagnetism in the pseudogap state of the cuprate Bi2Sr2CaCu2O8+δ superconductor in an intense magnetic field. Phys. Rev. Lett. 95, 247002 (2005).
Kohsaka, Y. et al. How Cooper pairs vanish approaching the Mott insulator in Bi2Sr2CaCu2O8+δ . Nature 454, 1072–1078 (2008).
Hanaguri, T. et al. Quasiparticle interference and superconducting gap in Ca2−xNaxCuO2Cl2 . Nat. Phys. 3, 865–871 (2007).
Kiss, T. et al. A versatile system for ultrahigh resolution, low temperature, and polarization dependent Laser-angle-resolved photoemission spectroscopy. Rev. Sci. Instrum. 79, 023106–023106 (2008).
Kordyuk, A., Borisenko, S., Knupfer, M. & Fink, J. Measuring the gap in angle-resolved photoemission experiments on cuprates. Phys. Rev. B 67, 064504 (2003).
Varma, C. M. & Zhu, L. Topological transition in the fermi surface of cuprate superconductors in the pseudogap regime. Phys. Rev. Lett. 98, 177004 (2007).
Chubukov, A. V., Norman, M. R., Millis, A. J. & Abrahams, E. Gapless pairing and the Fermi arc in the cuprates. Phys. Rev. B 76, 180501 (2007).
Norman, M. R., Randeria, M., Ding, H. & Campuzano, J. C. Phenomenology of the low-energy spectral function in high-T c superconductors. Phys. Rev. B 57, R11093 (1998).
Pasupathy, A. N. et al. Electronic origin of the inhomogeneous pairing interaction in the high-T c superconductor Bi2Sr2CaCu2O8+δ . Science 320, 196–201 (2008).
Tallon, J. L., Storey, J. G. & Loram, J. W. Fluctuations and critical temperature reduction in cuprate superconductors. Phys. Rev. B 83, 092502 (2011).
Kondo, T. et al. Disentangling Cooper-pair formation above the transition temperature from the pseudogap state in the cuprates. Nat. Phys. 7, 21–25 (2011).
Gomes, K. K. et al. Visualizing pair formation on the atomic scale in the high-T c superconductor Bi2Sr2CaCu2O8+δ . Nature 447, 569–572 (2007).
Barišic′, N. et al. Universal sheet resistance and revised phase diagram of the cuprate high-temperature superconductors. Proc. Natl Acad. Sci. USA 27, 8424 (2013).
Orenstein, J., Corson, J., Oh, S. & Eckstein, J. Superconducting fluctuations in Bi2Sr2Ca1−xDyxCu2O8+δ as seen by terahertz spectroscopy. Annalen der Physik 15, 596–605 (2006).
Bilbro, L. et al. Temporal correlations of superconductivity above the transition temperature in La2−xSrxCuO4 probed by terahertz spectroscopy. Nat. Phys. 7, 298–302 (2011).
Emery, V. & Kivelson, S. Importance of phase fluctuations in superconductors with small superfluid density. Nature 374, 434–437 (1995).
Shekhter, A. et al. Bounding the pseudogap with a line of phase transitions in YBa2Cu3Oδ . Nature 498, 75–77 (2013).
Kondo, T. et al. Anomalous doping variation of the nodal low-energy feature of superconducting (Bi,Pb)2(Sr,La)2CuO6+δ crystals revealed by laser-based angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 110, 217006 (2013).
Zhou, X. J. et al. High-temperature superconductors: universal nodal Fermi velocity. Nature 423, 398–398 (2003).
Pan, S. H. et al. Microscopic electronic inhomogeneity in the high-T c superconductor Bi2Sr2CaCu2O8+x . Nature 413, 282–285 (2001).
Acknowledgements
We thank M. Imada, S. Sakai and T. Misawa for useful discussions. This work is supported by JSPS (KAKENHI Grants No. 24740218 and No. 25220707, and FIRST Program).
Author information
Authors and Affiliations
Contributions
T.K. and S.S. designed the experiment. T.K. carried out ARPES experiment, and W.M. and Y.I. assisted the experimental setup. T.K. performed the data analysis. T.S., H.S., and T.Ta. grew the high-quality single crystals. T.K. and T.To. wrote the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-17, Supplementary Notes 1-9 and Supplementary References (PDF 8559 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kondo, T., Malaeb, W., Ishida, Y. et al. Point nodes persisting far beyond Tc in Bi2212. Nat Commun 6, 7699 (2015). https://doi.org/10.1038/ncomms8699
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms8699
This article is cited by
-
Laser-based angle-resolved photoemission spectroscopy with micrometer spatial resolution and detection of three-dimensional spin vector
Scientific Reports (2024)
-
Observation and quantification of the pseudogap in unitary Fermi gases
Nature (2024)
-
Absence of a BCS-BEC crossover in the cuprate superconductors
npj Quantum Materials (2023)
-
Unveiling phase diagram of the lightly doped high-Tc cuprate superconductors with disorder removed
Nature Communications (2023)
-
Witnessing light-driven entanglement using time-resolved resonant inelastic X-ray scattering
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.