Abstract
Single crystals of methylammonium lead trihalide perovskites (MAPbX3; MA=CH3NH3+, X=Br− or I−) have shown remarkably low trap density and charge transport properties; however, growth of such high-quality semiconductors is a time-consuming process. Here we present a rapid crystal growth process to obtain MAPbX3 single crystals, an order of magnitude faster than previous reports. The process is based on our observation of the substantial decrease of MAPbX3 solubility, in certain solvents, at elevated temperatures. The crystals can be both size- and shape-controlled by manipulating the different crystallization parameters. Despite the rapidity of the method, the grown crystals exhibit transport properties and trap densities comparable to the highest quality MAPbX3 reported to date. The phenomenon of inverse or retrograde solubility and its correlated inverse temperature crystallization strategy present a major step forward for advancing the field on perovskite crystallization.
Similar content being viewed by others
Introduction
Organo-lead trihalide hybrid perovskites (MAPbX3; MA=CH3NH3+, X=Br− or I−) have been widely investigated for solar cells1,2,3,4,5,6,7,8, lasing9, light-emitting diodes10, photodetectors11 and hydrogen production12. This considerable interest in organo-lead trihalide perovskites is because of their tunable optical properties, high-absorption coefficients, long-ranged balanced electron and hole transport13, low cost and facile deposition techniques14,15,16. In particular, single crystals of MAPbBr3 and MAPbI3 were shown to possess long carrier diffusion lengths and a remarkably low trap-state densities, which is comparable to the best photovoltaic-quality silicon17. These properties provide a view of the ultimate potential of hybrid perovskites, and make single crystals of MAPbX3 a highly desirable semiconductor for optoelectronic applications that are much broader than their polycrystalline thin film counterpart. However, the reported solution crystallization processes for perovskite single crystals suffer from very slow growth rates and no shape control over the resultant crystals17,18,19,20,21. The highest reported growth rate was estimated to be ∼26 mm3 per day (∼1 mm3 h−1), based on a MAPbI3 crystal with the dimensions of 10 mm × 10 mm × 8 mm that took a month to grow20. A radically faster crystallization technique that could also address the need for a diverse variety of crystal geometries will allow more extensive use of hybrid perovskite single crystals.
The choice of a suitable solvent medium has always been a defining factor for the quality of the ensuing crystals. In the case of hybrid perovskites, the most widely used solvents are γ-butyrolactone (GBL), N,N-dimethylformamide (DMF) and dimethylsulphoxide (DMSO). The solubility of PbX2 and MAX in these solvents or their mixtures was found to vary; hence, it was previously reported that MAPbBr3 crystallized more aptly from DMF while MAPbI3 crystallized better from GBL17. Perovskite crystallization from aqueous solution was also reported, in which crystals were formed, classically, on cooling a preheated solution20. It is generally the norm that solutes tend to have a higher degree of solubility at higher temperatures; hence, a good solvent for crystallization will dissolve more precursors when hot, while cooling down induces supersaturation commencing the crystallization. On the other hand, a decrease of solute solubility in solvents with increasing temperature (that is, inverse temperature or retrograde solubility) is a rare occurrence, that is, only displayed by a few materials22.
Here we show that MAPbX3 perovskites exhibit inverse temperature solubility behaviour in certain solvents. This novel phenomenon in hybrid perovskites enabled us to design an innovative crystallization method for these materials, referred to here as inverse temperature crystallization (ITC), to rapidly grow high-quality size- and shape-controlled single crystals of both MAPbBr3 and MAPbI3, at a rate that is an order of magnitude faster than the previously reported growth methods17,18,19,20,21. The versatility of our approach provides the continuous enlargement of crystals, through replacement of the depleted growth solution, and the use of templates for controlling their shapes.
Results
Single crystal growth and structural characterization
We noticed the rapid formation of small MAPbBr3 perovskite precipitates at high temperatures in some concentrated solutions (for example, DMF) and not in others (for example, DMSO). On the other hand, GBL could not be used as a solvent because of the very low solubility of MAPbBr3 (<0.05 g ml−1 at both room temperature and 80 °C). The effect of the different solvents could be related to their varying degrees of coordination with the precursors, as it was previously reported that DMSO may retard the crystallization process because of its strong binding to the lead precursor23,24,25.
Consequently, DMF was chosen for MAPbBr3 ITC. Through studying the solubility of MAPbBr3 in DMF, we observed that it drops markedly from 0.80±0.05 g ml−1 at room temperature to 0.30±0.05 g ml−1 at 80 °C. This inverse solubility phenomenon was used to crystallize MAPbX3 rapidly in hot solutions as illustrated in Fig. 1a. Through balancing both temperature and concentration of precursors in DMF, only a few crystals were formed. For instance, by setting the temperature of the heating bath at 80 °C usually <5 crystals are formed in case of 1 M solution of PbBr2 and MABr (Supplementary Fig. 1). Inspired by this observation, we repeated the same procedure and studied different solvents that could lead to the same effect in MAPbI3. Unlike MAPbBr3, ITC of MAPbI3 was only possible in GBL solution, while no precipitates were observed in the case of DMF or DMSO.
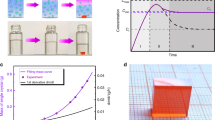
(a) Schematic representation of the ITC apparatus in which the crystallization vial is immersed within a heating bath. The solution is heated from room temperature and kept at an elevated temperature (80 °C for MAPbBr3 and 110 °C for MAPbI3) to initiate the crystallization. (b,c) MAPbI3 and MAPbBr3 crystal growth at different time intervals. (d,e) Powder X-ray diffraction of ground MAPbBr3 and MAPbI3 crystals. Insets: pictures of the corresponding crystals grown within a non-constraining vessel geometry.
As expected, we observed that the crystallization process in both MAPbBr3 and MAPbI3 is reversible and the crystals dissolve back when cooled to room temperature. It is also worth mentioning that individual precursors PbX2 and MAX did not show any inverse solubility behaviour (that is, saturated solutions of the individual precursor did not show precipitation on heating), implying that the phenomenon is tied to the perovskite structure.
The growth process of MAPbI3 crystal using the ITC technique was recorded on video using time-accelerated mode (Supplementary Movie 1), several snapshots of which are shown in Fig. 1b. Individual MAPbI3 crystal was calculated to grow at a rate of ∼3 mm3 h−1 for the first hour, a rate that significantly increases to ∼9 mm3 h−1 for the second hour and to ∼20 mm3 h−1 for the following hour. This value is an order of magnitude greater than the previously reported highest growth rate20. An even faster growth rate was observed for MAPbBr3 crystals, reaching up to 38 mm3 h−1 for the third hour (Fig. 1c), resulting in a higher yield in comparison with MAPbI3. Powder X-ray diffraction patterns of the ground crystals demonstrate pure perovskite phase for both MAPbBr3 and MAPbI3 (Fig. 1d,e). Single-crystal X-ray diffraction analysis showed a good match with previous single crystals grown at room temperature using antisolvent vapour-assisted crystallization17 (Supplementary Table 1). Scanning electron microscopy images of the cleaved crystals show the absence of any grain boundaries, indicating the single-crystalline nature of both crystals (Supplementary Fig. 2).
Further growth of the crystal was achieved by carefully removing the crystal and placing it in a fresh 1 M solution of the precursors (Fig. 2a). As shown in Supplementary Movie 2 for MAPbBr3, we observed a possible shape control of the crystal by the geometry of crystallization vessel. Hence, single crystals of MAPbBr3 and MAPbI3 were synthesized with a number of different shapes by changing the geometry of the vessel in which crystallization takes place (Fig. 2b).
(a) Continuous growth of an MAPbBr3 crystal by moving the crystal into a larger vial with a fresh growth solution. (b) Shape-controlled crystals of MAPbBr3 (orange) and MAPbI3 (black) by varying the geometry of the confining vessel. From left to right—crystals grown in a round-bottom test tube and a 2-mm cuvette.
Optical and transport properties
Further, we investigated optical and transport properties of the crystals, demonstrating that MAPbX3 obtained using ITC in few hours are comparable quality to previously reported crystals grown in several weeks. From the steady-state absorption measurements a sharp band edge is observed (Fig. 3a,b). Band gaps extracted from Tauc plots show values of 2.18 and 1.51 eV for MAPbBr3 and MAPbI3, respectively. The band gap values for crystals grown using ITC are in a good agreement with the values reported for single crystals grown at room temperature through antisolvent vapour-assisted crystallization17. The photoluminescence peak position of MAPbBr3 and MAPbI3 single crystals is located at 574 and 820 nm, respectively, matching the values reported earlier for the same single crystals grown using antisolvent vapour-assisted crystallization17.
To investigate the excited-state lifetime of these single crystals, we monitored both the ground-state bleach recovery and the excited-state absorption in the nano- and microsecond time regime using nanosecond transient absorption spectroscopy with broadband capabilities. Two time components are observed for both single crystals. A fast component of τ≈28±5 ns and τ≈18±6 ns together with a slower decay of τ≈300±26 ns and τ≈570±69 ns were measured for MAPbBr3 and MAPbI3 crystals, respectively. These measured surface (fast component) and bulk (slow component) carrier lifetimes are in good agreement with the ones reported recently for the same kinds of single crystals17.
The carrier mobility μ (μ=μp≈μn, where μp and μn are hole and electron mobility, respectively, as MAPbX3 is an intrinsic semiconductor)26 of MAPbX3 (X=Br−, I−) was estimated from the dark current–voltage (I–V)characteristics, following the standard space charge-limited current model. The I–V traces showed the Mott–Gurney’s power law dependence, for instance, an Ohmic region at the lower and a space charge-limited current model at higher bias. A quadratic dependence of the transition from the Ohmic to Child’s law through the trap filled limit (TFL) was observed in both MAPbBr3 and MAPbI3 crystals. The carrier mobilities and the trap densities (ntraps) were estimated to be 24.0 cm2 V−1 s−1 and 3 × 1010 cm−3 for MAPbBr3 crystals (Fig. 4c), as well as 67.2 cm2 V−1 s−1 and 1.4 × 1010 cm−3 for MAPbI3 crystals (Fig. 4d).
(a,b) Transient absorption of (a) MAPbBr3 and (b) MAPbI3 crystals. (c,d) I–V of perovskite crystals exhibiting different regions obtained from the log I versus log V plots. The regions are marked for Ohmic (IαVn=1), TFL (IαVn>3) and Child’s regime (IαVn=2). The trap densities were calculated from the Child’s regime shown in (c,d).
We calculated the carrier diffusion length by combining carrier lifetime with mobility LD=(μτkBT/e)1/2 (where kB is Boltzmann’s constant and T is the sample’s temperature). By using the longer carrier lifetime (bulk component), a best-case carrier diffusion length was calculated to be ∼4.3 μm for MAPbBr3 and ∼10.0 μm for MAPbI3. A worst-case diffusion length could be estimated from the shorter carrier lifetime, corresponding to the surface component: ∼1.3 and ∼1.8 μm for MAPbBr3 and MAPbI3, respectively. Hence, despite the rapid rate with which crystals were grown via ITC, their transport characteristics together with trap-state densities are comparable to single crystals prepared with classical techniques, which were grown over a much longer period of time.
Discussion
We observed experimentally that perovskite crystals formed in the precursor solution at elevated temperatures dissolved back when the solution temperature was decreased to room temperature. This observation demonstrates that the thermodynamic stability of a precipitated hybrid perovskite compound has seemingly paradoxical temperature dependence, since simple monomolecular compounds are expected to dissolve at higher temperatures. Therefore, it is instructive to analyse how such a situation may arise. We hypothesize that this phenomenon might be related to the formation of complexes of precursors (whose nature is not the subject of this report and is under intensive study) or their products with the solvent23,27,28. The theory presented below illustrates how these complexes can affect the temperature-dependent stability of the precipitate and reverse its effect depending on the different parameters of the system.
Suppose there is only one type of molecular precursor controlling the crystallization of a complex compound such as a perovskite, then the formation of complexes involving the precursor molecule and solvent molecules may significantly affect the precipitation of the compound. To illustrate this situation we analyse the thermodynamic stability of a monomolecular precipitate made of molecules A in the solution, where molecules A can form complexes with solvent molecules, the complex’s binding energy being ɛC. As an ultimate stable state always contains only one precipitated particle, and to avoid secondary issues related to crystal facets, we assume that a single precipitated A-particle is placed in a unit volume of solution and has a spherical shape.
In general, the stability of precipitated solids in a solution is determined by several conditions based on the balance of chemical potentials of all its molecular or atomic constituents present in the solution and in the solid form. These conditions must also take into account the presence of complexes formed by the constituents in the solution. In our case, these conditions are the equality of the chemical potentials of A-molecules in the particle and solution (that is, μP=μA), and of the complex’s chemical potential, μC, and the sum of chemical potentials for all complex constituents (one A-molecule and j solvent molecules); that is, μC=jμS+μA. Expressed in terms of concentrations and binding energies, these conditions read (Supplementary Note 1 for details):

where ɛ is the cohesive energy of A-molecule in the particle, γ is the surface energy per A-molecule, R is the particle radius measured in terms of the characteristic intermolecular distance, T is the solution temperature, nC and nA are the number concentrations in the solution; and vC, vA and vS are the characteristic volumes of the complex, A-molecule and solvent molecule, respectively. Resolving equation (1) with respect to concentrations gives:

To simplify the analysis we consider the limit when the particle size is large enough, that is, far from its critical value. In that case, the surface energy contributions in the exponents of equation (2) can be neglected, that is, we take the limit γ→0. The total number concentration mC of all A-molecules consists of the part nP forming the particle, the part nC forming complexes and the part nA of individual molecules in the solution such that mA=nP+nC+nA. Using these constraints and equation (2) we obtain for the number fraction of precipitated A-molecules, npvA:

To illustrate the effect of temperature on nP, it is convenient to analyse the derivative of equation (3):

If dnP/dT<0 then it would mean that the precipitated mass (that is, A-particle size) decreases with increasing temperature—the situation typically observed for most materials precipitating from solution. In contrast, if dnP/dT>0 an interesting situation occurs in which an increase in temperature results in an increase in the precipitated number of A-molecules, as observed experimentally for hybrid perovskites. This effect, as can be seen from equation (4), takes place if

or if we accept that  (that is, large enough ɛC/T ratio), then the inequality given by equation (5) reduces to ɛC>ɛ. These analytical relation can be further understood in physical terms as follows: at low temperatures most of the A-molecules are bound in the complexes with the solvent; therefore, the solution has no supersaturation in terms of concentration of unbound A-molecules. When the temperature increases, the concentration of unbound A-molecules increases (because of dissociation of the complexes) and may reach the supersaturation, thus triggering the precipitation of A-particles. Conversely, when the temperature of the solution containing the precipitated A-particle is decreased, the concentration nA of unbound A-molecules is also decreased because of formation of many more complexes with solvent. This decrease in nA makes the solution too diluted in A-molecules such that the particle has to transfer some molecules to the solution, that is, it dissolves. It should be noted that the process of crystallization is endothermic with respect to A-molecules, as a molecule moves from the complex with higher binding energy to the precipitate, where its binding (cohesive) energy is lower. Therefore, the crystallization reaction consumes thermal energy.
(that is, large enough ɛC/T ratio), then the inequality given by equation (5) reduces to ɛC>ɛ. These analytical relation can be further understood in physical terms as follows: at low temperatures most of the A-molecules are bound in the complexes with the solvent; therefore, the solution has no supersaturation in terms of concentration of unbound A-molecules. When the temperature increases, the concentration of unbound A-molecules increases (because of dissociation of the complexes) and may reach the supersaturation, thus triggering the precipitation of A-particles. Conversely, when the temperature of the solution containing the precipitated A-particle is decreased, the concentration nA of unbound A-molecules is also decreased because of formation of many more complexes with solvent. This decrease in nA makes the solution too diluted in A-molecules such that the particle has to transfer some molecules to the solution, that is, it dissolves. It should be noted that the process of crystallization is endothermic with respect to A-molecules, as a molecule moves from the complex with higher binding energy to the precipitate, where its binding (cohesive) energy is lower. Therefore, the crystallization reaction consumes thermal energy.
The temperature behaviour described by equation (5) provides a qualitative framework to explain the effects observed experimentally for perovskite materials. A quantitative analysis requires a detailed investigation of the molecular content of the precursor solution, a subject of future research.
In summary, we report the novel observation of inverse solubility of hybrid organo-lead trihalide perovskites. A careful choice of solvent, temperature and other parameters made it possible to utilize this method to rapidly grow single crystals of MAPbBr3 and MAPbI3 in hot solutions via ITC. Despite the fact that these crystals grow very fast, they exhibit carrier transport properties comparable to those grown by the usual cooling or antisolvent vapour-assisted crystallization techniques. The ‘quantum leap’ in crystal growth rates in ITC, over the previously reported growth methods so far used for single crystal-hybrid perovskites, represents a major breakthrough in the field of perovskite single crystals for enabling the wide applications of these remarkable semiconductor materials.
Methods
Chemicals and reagents
Lead bromide (≥98%), lead iodide (99.999% trace metal basis), DMF (anhydrous, 99.8%) and GBL (≥99%) were purchased from Sigma Aldrich. MABr and MAI were purchased from Dyesol Limited (Australia). All salts and solvents were used as received without any further purification.
Synthesis of MAPbX3 single crystals
One molar solution containing PbX2 and MAX was prepared in DMF or GBL for X=Br−, I−, respectively. The bromide solution was prepared at room temperature, whereas the iodide solution was heated up to 60 °C. The solutions were filtered using PTFE filter with 0.2-μm pore size. Two millilitres of the filtrate were placed in a vial and the vial was kept in an oil bath undisturbed at 80 and 110 °C for Br- and I-based perovskites, respectively. All procedures were carried out under ambient conditions and humidity of 55–57%. The crystals used for measurements were grown for 3 h. The reaction yield for MAPbBr3 and MAPbI3 was calculated to be 35 and 11 wt %, respectively.
Measurement and characterization
Powder X-ray diffraction was performed on a Bruker AXS D8 diffractometer using Cu-Kα radiation. Single-crystal X-ray diffraction was performed on Bruker D8 Venture, CMOS detector, microfocus copper source. The steady-state absorption and photoluminescence were recorded using Cary 6000i spectrophotometer with an integrating sphere and Edinburgh Instrument spectrofluorometer, respectively. Time-resolved transient absorption decays were measured with a femto-nanoseconds pump−probe set-up. The excitation pulse at 480 nm was generated using a spectrally tunable optical Parametric Amplifier (Light Conversion LTD) integrated to a Ti:sapphire femtosecond regenerative amplifier operating at 800 nm with 35 fs pulses and a repetition rate of 1 kHz. The white light probe pulse, on the other hand, was generated by a super continuum source29,30. The pump and probe beams were overlapped spatially and temporally on the sample, and the transmitted probe light from the samples was collected and focused on the broad-band ultraviolet–visible-near-infrared detectors to record the time-resolved excitation-induced difference spectra. I–V characteristics were carried out in the dark under vacuum (∼10−4 mbar) at 300 K, in the simple two electrode configuration (Au/MAPbX3/Au). The perovskite crystal was sandwiched between the rectangular electrodes (3 mm × 2 mm) Au (100 nm), deposited on both sides of the single crystal, by an Angstrom thermal evaporator at a 0.5 Å s−1 deposition rate. The thickness and rate of deposition during the evaporation of Au contact was monitored by an Inficon thickness monitor. The thickness of MAPbBr3 and MAPbI3 crystals were measured as 2.32 and 2.49 mm, respectively, by the digital Vernier caliper. The typical nonlinear dark current, voltage plots followed the Lampert’s theory, where the current was found to be limited by the trap-assisted space charge conduction. Onset voltage (VTFL) for the TFL was used for the calculation (equation (6)) of density of traps (ntraps) in the perovskite crystals

where q is the electronic charge, d is the thickness of the crystal, ɛ is the dielectric constant of the material (25.5 for MAPbBr3 and 32 for MAPbI3)19,31 and ɛo is the vacuum permittivity.
Additional information
How to cite this article: Saidaminov, M. I. et al. High-quality bulk hybrid perovskite single crystals within minutes by inverse temperature crystallization. Nat. Commun. 6:7586 doi: 10.1038/ncomms8586 (2015).
References
Docampo, P., Ball, J. M., Darwich, M., Eperon, G. E. & Snaith, H. J. Efficient organometal trihalide perovskite planar-heterojunction solar cells on flexible polymer substrates. Nat. Commun. 4, 2761 (2013).
Kim, H. S. et al. Mechanism of carrier accumulation in perovskite thin-absorber solar cells. Nat. Commun. 4, 2242 (2013).
Stranks, S. D. et al. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 342, 341–344 (2013).
Mei, A. et al. A hole-conductor-free, fully printable mesoscopic perovskite solar cell with high stability. Science 345, 295–298 (2014).
Christians, J. A., Fung, R. C. M. & Kamat, P. V. An inorganic hole conductor for organo-lead halide perovskite solar cells. improved hole conductivity with copper iodide. J. Am. Chem. Soc. 136, 758–764 (2014).
Liu, D., Yang, J. & Kelly, T. L. Compact layer free perovskite solar cells with 13.5% efficiency. J. Am. Chem. Soc. 136, 17116–17122 (2014).
Nie, W. et al. High-efficiency solution-processed perovskite solar cells with millimeter-scale grains. Science 347, 522–525 (2015).
Choi, J. J., Yang, X., Norman, Z. M., Billinge, S. J. L. & Owen, J. S. Structure of methylammonium lead iodide within mesoporous titanium dioxide: active material in high-performance perovskite solar cells. Nano Lett. 14, 127–133 (2014).
Xing, G. et al. Low-temperature solution-processed wavelength-tunable perovskites for lasing. Nat. Mater. 13, 476–480 (2014).
Tan, Z.-K. et al. Bright light-emitting diodes based on organometal halide perovskite. Nat. Nano 9, 687–692 (2014).
Dou, L. et al. Solution-processed hybrid perovskite photodetectors with high detectivity. Nat. Commun. 5, 5404 (2014).
Chen, Y.-S., Manser, J. S. & Kamat, P. V. All solution-processed lead halide perovskite-BiVO4 tandem assembly for photolytic solar fuels production. J. Am. Chem. Soc. 137, 974–981 (2015).
Xing, G. et al. Long-range balanced electron- and hole-transport lengths in organic-inorganic CH3NH3PbI3 . Science 342, 344–347 (2013).
Noh, J. H., Im, S. H., Heo, J. H., Mandal, T. N. & Seok, S. I. Chemical management for colorful, efficient, and stable inorganic–organic hybrid nanostructured solar cells. Nano Lett. 13, 1764–1769 (2013).
Filip, M. R., Eperon, G. E., Snaith, H. J. & Giustino, F. Steric engineering of metal-halide perovskites with tunable optical band gaps. Nat. Commun. 5, 5757 (2014).
D’Innocenzo, V., Kandada, A. R. S., De Bastiani, M., Gandini, M. & Petrozza, A. Tuning the light emission properties by band gap engineering in hybrid lead halide perovskite. J. Am. Chem. Soc. 136, 17730–17733 (2014).
Shi, D. et al. Low trap-state density and long carrier diffusion in organolead trihalide perovskite single crystals. Science 347, 519–522 (2015).
Stoumpos, C. C., Malliakas, C. D. & Kanatzidis, M. G. Semiconducting tin and lead iodide perovskites with organic cations: phase transitions, high mobilities, and near-infrared photoluminescent properties. Inorg. Chem. 52, 9019–9038 (2013).
Dong, Q. et al. Electron-hole diffusion lengths >175 μm in solution-grown CH3NH3PbI3 single crystals. Science 347, 967–970 (2015).
Dang, Y. et al. Bulk crystal growth of hybrid perovskite material CH3NH3PbI3 . Cryst. Eng. Commun. 17, 665–670 (2015).
Baikie, T. et al. Synthesis and crystal chemistry of the hybrid perovskite (CH3NH3) PbI3 for solid-state sensitised solar cell applications. J. Mater. Chem. A 1, 5628–5641 (2013).
So¨hnel, O. & Novotný, P. Densities of Aqueous Solutions of Inorganic Substances Elsevier (1985).
Wu, Y. et al. Retarding the crystallization of PbI2 for highly reproducible planar-structured perovskite solar cells via sequential deposition. Energy Environ. Sci. 7, 2934–2938 (2014).
Miyamae, H., Numahata, Y. & Nagata, M. The crystal structure of lead(II) iodide-dimethylsulphoxide(1/2), PbI2(dmso)2 . Chem. Lett. 9, 663–664 (1980).
Wakamiya, A. et al. Reproducible fabrication of efficient perovskite-based solar cells: X-ray crystallographic studies on the formation of CH3NH3PbI3 layers. Chem. Lett. 43, 711–713 (2014).
Giorgi, G. & Yamashita, K. Organic–inorganic halide perovskites: an ambipolar class of materials with enhanced photovoltaic performances. J. Mater. Chem. A 3, 8981–8991 (2015).
Stamplecoskie, K. G., Manser, J. S. & Kamat, P. V. Dual nature of the excited state in organic-inorganic lead halide perovskites. Energy Environ. Sci. 8, 208–215 (2015).
Jeon, N. J., Noh, J. H., Kim, Y. C., Yang, W. S., Ryu, S. & Seok, S. I. Solvent engineering for high-performance inorganic-organic hybrid perovskite solar cells. Nat. Mater. 13, 897–903 (2014).
Bose, R. et al. Direct femtosecond observation of charge carrier recombination in ternary semiconductor nanocrystals: the effect of composition and shelling. J. Phys. Chem. C 119, 3439–3446 (2015).
Mohammed, O. F., Xiao, D., Batista, V. S. & Nibbering, E. T. J. Excited-state intramolecular hydrogen transfer (ESIHT) of 1,8-Dihydroxy-9,10-anthraquinone (DHAQ) characterized by ultrafast electronic and vibrational spectroscopy and computational modeling. J. Phys. Chem. A 118, 3090–3099 (2014).
Poglitsch, A. & Weber, D. Dynamic disorder in methylammoniumtrihalogenoplumbates (II) observed by millimeter‐wave spectroscopy. J. Chem. Phys. 87, 6373–6378 (1987).
Acknowledgements
We acknowledge the support of Awards URF/1/2268-01-01, URF/1/1741-01-01 and URF/1/1373-01-01 made by the King Abdullah University of Science and Technology (KAUST).
Author information
Authors and Affiliations
Contributions
M.I.S. and A.L.A. conceived the idea, developed the single-crystal growth, provided samples for all measurements, measured and analysed powder X-ray diffraction. I.D. and B.M. measured the steady-state PL and ultraviolet–visible. W.P. and Y.H. conducted single-crystal X-ray diffraction characterization. E.A. and O.F.M. conducted and analysed the TA measurement. B.M., L.W., O.F.M. and T.W. designed, performed and analysed the measurements of mobility and I–V trap-state density. G.M. assisted with the experimental synthesis. V.M.B. and A.G. did the theoretical studies. O.M.B. crafted and directed the overall research plan. M.I.S., A.L.A., V.M.B. and O.M.B. co-wrote the manuscript. All authors read and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Figures, Supplementary Table, Supplementary Note and Supplementary References
Supplementary Figures 1-2, Supplementary Table 1, Supplementary Note 1 and Supplementary References (PDF 514 kb)
Supplementary Movie 1
Time-accelerated video of MAPbI3 crystal growth from 1 M solution of MAPbI3 in GBL by Inverse Temperature Crystallization at 110 °C. (MOV 12177 kb)
Supplementary Movie 2
Time-accelerated video of MAPbBr3 crystal growth from 1 M solution of MAPbBr3 in DMF by Inverse Temperature Crystallization at 80 °C (MOV 7499 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Saidaminov, M., Abdelhady, A., Murali, B. et al. High-quality bulk hybrid perovskite single crystals within minutes by inverse temperature crystallization. Nat Commun 6, 7586 (2015). https://doi.org/10.1038/ncomms8586
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms8586
This article is cited by
-
Defect passivation in methylammonium/bromine free inverted perovskite solar cells using charge-modulated molecular bonding
Nature Communications (2024)
-
The effect of the PbI\(_2\) surface passivation on the leakage current for MAPbI\(_3\) single crystal nuclear detectors
Journal of Materials Science: Materials in Electronics (2024)
-
High-performance TiO2/perovskite solar cell based GO as hole transport layer
Journal of Materials Science: Materials in Electronics (2024)
-
Doping suppresses lattice distortion of vacant quadruple perovskites to activate self-trapped excitons emission
Nano Research (2024)
-
Growth and efficiency of MAPbBr3 based perovskite solar cells: insight from experimental and simulation
Indian Journal of Physics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.