Abstract
Actively sought since the turn of the century, two-dimensional quantum spin liquids (QSLs) are exotic phases of matter where magnetic moments remain disordered even at zero temperature. Despite ongoing searches, QSLs remain elusive, due to a lack of concrete knowledge of the microscopic mechanisms that inhibit magnetic order in materials. Here we study a model for a broad class of frustrated magnetic rare-earth pyrochlore materials called quantum spin ices. When subject to an external magnetic field along the [111] crystallographic direction, the resulting interactions contain a mix of geometric frustration and quantum fluctuations in decoupled two-dimensional kagome planes. Using quantum Monte Carlo simulations, we identify a set of interactions sufficient to promote a groundstate with no magnetic long-range order, and a gap to excitations, consistent with a Z2 spin liquid phase. This suggests an experimental procedure to search for two-dimensional QSLs within a class of pyrochlore quantum spin ice materials.
Similar content being viewed by others
Introduction
In a two-dimensional (2D) quantum spin liquid (QSL) state, strong quantum fluctuations prevent the ordering of magnetic spins, even at zero temperature. The resulting disordered phase can potentially be a remarkable state of matter, supporting a range of exotic quantum phenomena. Some, such as emergent gauge structures and fractional charges, are implicated in a wide range of future technologies like high-temperature superconductivity1,2 and topological quantum computing3. It is therefore remarkable that, despite extensive examination of the basic theoretical ingredients required to promote a 2D QSL in microscopic models4,5, the state remains elusive, with only a few experimental candidates existing today6,7.
Recently, the search for QSL states has turned to consider quantum fluctuations in the so-called spin ice compounds8. In these systems, magnetic ions reside on a pyrochlore lattice—a non-Bravais lattice consisting of corner-sharing tetrahedra. Classical magnetic moments (described by Ising spins) on the pyrochlore lattice can be geometrically frustrated at low temperatures, leading to spin configurations that obey the so-called ‘ice rules’, a mapping to the proton-disorder problem in water ice9. The ice rules result in a large set of degenerate ground states—a classical spin liquid with a finite thermodynamic entropy per spin10,11. Two canonical materials, Ho2TiO7 and Dy2Ti2O7, have been demonstrated to manifest spin ice behaviour, and experiments and theory enjoy a healthy dialogue due to the existence of classical microscopic models capable of describing a wide range of experimental phenomena10.
Classical spin ice pyrochlores are conjectured to lead to QSLs in the presence of the inevitable quantum fluctuations at low temperatures4,8. The effects of certain types of quantum fluctuations on the spin ice state have been investigated theoretically12 and numerically13,14, where they have been demonstrated to lift the classical degeneracy and promote a three-dimensional (3D) QSL phase with low-energy gapless excitations that behave like photons12,13. In several related pyrochlore compounds, particularly Tb2Ti2O7, Yb2Ti2O7, Pr2Zr2O7 and Pr2Sn2O7, quantum effects have been observed, which make them natural candidates to search for such 3D QSLs15,16,17. In an attempt to elucidate the microscopic underpinnings of these and related materials, recent theoretical studies have produced a general low-energy effective spin-1/2 model for magnetism in rare earth pyrochlores18,19,20. In an important development, Huang, Chen and Hermele21 have shown that, on the pyrochlore lattice, strong spin-orbit coupling can lead to Kramers doublets with dipolar-octupolar character in d- and f-electron systems. This allows for a specialization of the general effective model to one without the debilitating ‘sign problem’—amenable to solution through quantum Monte Carlo (QMC) methods—thus admitting a systematic search for QSL phases via large-scale computer simulations. Using large-scale QMC simulations, we show that a two-dimensional model on the kagome lattice descending from the quantum Hamiltonian discussed by Huang, Chen and Hermele21 exhibits an exotic disordered phase—a quantum kagome ice state—in a wide range of Hamiltonian parameters. Such a state displays exponentially decaying correlations and is consistent with a gapped QSL phase. These results suggest an alternative experimental route to search for the long-sought QSL phase in two dimensions starting from quantum spin ice pyrochlore materials subject to an external field along the [111] direction.
Results
A quantum kagome ice model
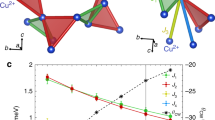
While the possibility for 3D QSLs in the above compounds is intriguing, spin ice materials offer a compelling mechanism for dimensional reduction to 2D, since single-ion anisotropy constrains magnetic moments to point along the local tetrahedral symmetry axes in the pyrochlore lattice. This mechanism consists of the application of an external magnetic field along the global [111] crystallographic direction that partially lifts the spin ice degeneracy by pinning one spin per tetrahedron. As illustrated in Fig. 1a, this [111] magnetic field effectively decouples spins between the alternating kagome and triangular layers of the original pyrochlore structure. To simplest approximation, the system becomes a two-dimensional system of stacked kagome planes22,23,24,25, where spins on the intervening triangular planes align in the direction of the field (becoming energetically removed from the problem), while those in the kagome plane (Fig. 1b) remain partially disordered. These kagome spins retain a fraction of the zero-field spin ice entropy, though still preserving the spin ice rules (two-in, two-out) of the parent pyrochlore system. This leads to classically disordered state, termed kagome ice22,24,25,26, evidenced to date in several experimental studies on spin ice materials27,28,29.
(a) The pyrochlore lattice viewed as a set of alternating kagome (blue) and triangular (green) layers along the [111] direction. Spins on the pyrochlore lattice (blue arrows) satisfy the ‘ice rules’: two-in, two-out of each tetrahedron. (b) Two-dimensional projection of the pyrochlore spin configuration onto a kagome plane (blue arrows). At the centre of each triangle is a representation of the out-of-plane spin: dots (crosses) refer to a spin pointing inwards (outwards) of each tetrahedron in a. (c) The associated pseudo-spin  configuration where filled (empty) circles represents a pseudo-spin up (down). Our quantum Monte Carlo simulations of the pseudo-spin Hamiltonian are defined on periodic tori spanned by the primitive vectors a1 and a2, where ‖a1‖=‖a2‖=2.
configuration where filled (empty) circles represents a pseudo-spin up (down). Our quantum Monte Carlo simulations of the pseudo-spin Hamiltonian are defined on periodic tori spanned by the primitive vectors a1 and a2, where ‖a1‖=‖a2‖=2.
The above observations lead to a natural microscopic mechanism to search for 2D QSL behaviour30. First, one begins with classical nearest-neighbour spin ice in an applied [111] field, so as to promote the aforementioned kagome ice state. This model maps to a projected pseudo-spin Ising model with a symmetry-breaking Zeeman field h, arising from a combination of the physical [111] field and the original pyrochlore spin exchange interaction (Fig. 1c). For moderate h, the classical ground state retains an extensive degeneracy, before becoming a fully polarized ferromagnetic state for h/Jz >2. Next, to include the effect of quantum fluctuations, one may add exchanges from the recent quantum spin ice models18,19,20,21. We consider only those quantum fluctuations discussed by Huang et al.21, to obtain a pseudo-spin Hamiltonian on the kagome lattice,

Here, Sr are spin-1/2 operators, with a global z axis ( and
and  in Fig. 1c). This Hamiltonian cannot be solved exactly by analytical techniques; however large-scale QMC simulations are possible in a parameter regime (J±≥0) devoid of the prohibitive sign problem.
in Fig. 1c). This Hamiltonian cannot be solved exactly by analytical techniques; however large-scale QMC simulations are possible in a parameter regime (J±≥0) devoid of the prohibitive sign problem.
One can imagine a 2D QSL state arising conceptually by considering the quantum fluctuations J± and J±± as perturbations on the classical kagome ice limit, where only diagonal terms Jz>0 and  are present. Previously, large-scale QMC simulations have been performed on the kagome model in the limit J±>0 and J±±=0 (refs 31, 32) (a parameter regime where the Hamiltonian retains U(1) invariance). In that case, quantum fluctuations promote an in-plane ferromagnetic (FM) phase for h=0, and a valence bond-solid (VBS—a conventional symmetry broken phase) for h>0. Thus, it happens that fluctuations of the form induced by J± are not sufficient to promote a 2D QSL state.
are present. Previously, large-scale QMC simulations have been performed on the kagome model in the limit J±>0 and J±±=0 (refs 31, 32) (a parameter regime where the Hamiltonian retains U(1) invariance). In that case, quantum fluctuations promote an in-plane ferromagnetic (FM) phase for h=0, and a valence bond-solid (VBS—a conventional symmetry broken phase) for h>0. Thus, it happens that fluctuations of the form induced by J± are not sufficient to promote a 2D QSL state.
However, there remains the theoretical possibility of a gapped Z2 QSL phase promoted by the J±± quantum fluctuations. As detailed in the Supplementary Note 1 and Supplementary Fig. 1, the local constraints of classical kagome ice can be translated into a charge-free condition on the dual honeycomb lattice. Then, the full Hamiltonian (1) can be re-cast as a system of interacting bosonic spinons coupled to a compact U(1) gauge field on the dual lattice. In the limit of J±=0, this theory is expected to exhibit two distinct phases. One is a confined phase, corresponding to a conventional spin-ordered state; the other is a deconfined Z2 QSL phase20,21,33. From these simple arguments it is conceivable that these two phases exist in the phase diagram of equation (1). In the next section, we set J±=0 and explore this possibility for all parameter regimes J±±/Jz and h/Jz, using non-perturbative, unbiased QMC simulations. Before proceeding with the description of the QMC results, we emphasize that neither our simulations nor the analysis of the resulting lattice gauge theory are restricted to states within the ice manifold.
Quantum Monte Carlo results
We implement a finite-temperature Stochastic Series Expansion34,35,36 (SSE) QMC algorithm with directed loop updates in a 2+1 dimensional simulation cell, designed specifically to study the Hamiltonian equation (1) with J±=0 (for details, see the Methods Summary). Note, this Hamiltonian explicitly breaks U(1) invariance, retaining global Z2 symmetries. By a canonical transformation, S±→±iS±; we simulate only J±±<0, without loss of generality21. Various measurements are possible in this type of QMC simulation. Simplest are the standard SSE estimators for energy, magnetization  , and uniform spin susceptibility
, and uniform spin susceptibility  . The latter two allow us to map out the broad features of the phase diagram. Further, we measure the off-diagonal spin structure factor37
. The latter two allow us to map out the broad features of the phase diagram. Further, we measure the off-diagonal spin structure factor37

Here, ri points to the sites of the underlying triangular lattice (containing Ns sites) of the kagome lattice (containing V=3 × Ns sites). The vectors α are the position of each site within the unit cell with respect to the vector ri. This quantity allows us to define, for this spin Hamiltonian, the analogue of a condensate fraction in bosonic systems38,39, which detects transverse magnetic ordering. We define  as the ratio of largest eigenvalue nM of the one-body density matrix
as the ratio of largest eigenvalue nM of the one-body density matrix  to the number of sites V. The eigenvalues of ρi,j coincide with
to the number of sites V. The eigenvalues of ρi,j coincide with  for a translationally invariant system.
for a translationally invariant system.
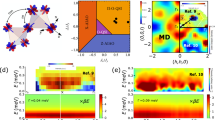
Figure 2a shows the QMC phase diagram for the J±=0 model of equation (1), using data for the condensate fraction f0. Careful finite-temperature and finite-size scaling, performed up to lattice sizes of V=L × L × 3=39 × 39 × 3 and β=Jz/T=96, is detailed in the Supplementary Information (Supplementary Figs 2 and 3 and Supplementary Note 2). The magnetization curve and the uniform spin susceptibility across the phase boundary at fixed h/Jz=0.833 are presented in Fig. 2a,b. The data clearly indicate the existence of two magnetized lobes on the phase diagram for J±±/Jz<0.5 and h/Jz≠0, where the zero-momentum condensate fraction of a surrounding FM phase is destroyed by a phase transition (which appears to be first order). The lobes have magnetizations of m≈−1/6 and m≈+1/6 for h/Jz<0 and h/Jz>0, respectively. The FM phase has a finite uniform susceptibility χz, while the lobe phases retain a small but finite χz that can be understood by the nature of the quantum fluctuation  as a spin pair interaction, which does not conserve the total magnetization
as a spin pair interaction, which does not conserve the total magnetization  . As discussed above, the phase in these lobes is a candidate for supporting a 2D QSL state.
. As discussed above, the phase in these lobes is a candidate for supporting a 2D QSL state.
(a) Phases of the two-dimensional quantum kagome ice model for J±=0 as a function of h/Jz and J±±/Jz. The colour scale represents the zero-momentum occupation f0 obtained from a Ns= 6 × 6 lattice and temperature T=Jz/24. In the quantum kagome ice lobes (QKI),  and
and  , whereas in the ferromagnetic (FM) phase
, whereas in the ferromagnetic (FM) phase  . Magnetization (b) and uniform susceptibility (c) as a function of J±±/Jz entering the candidate Z2 quantum spin liquid lobe at fixed h/Jz=0.833. Ns=6 × 6, 12 × 12, 18 × 18 and 24 × 24 are represented by orange squares, red crosses, purple circles and blue down triangles, respectively. Solid lines are guides to the eye. The error bars represent the one s.d. statistical uncertainty. Note that a fully spin-polarized phase occurs for h/Jz≥2, which is not illustrated in this phase diagram.
. Magnetization (b) and uniform susceptibility (c) as a function of J±±/Jz entering the candidate Z2 quantum spin liquid lobe at fixed h/Jz=0.833. Ns=6 × 6, 12 × 12, 18 × 18 and 24 × 24 are represented by orange squares, red crosses, purple circles and blue down triangles, respectively. Solid lines are guides to the eye. The error bars represent the one s.d. statistical uncertainty. Note that a fully spin-polarized phase occurs for h/Jz≥2, which is not illustrated in this phase diagram.
To examine this hypothesis, we perform a detailed search for ordered structures in the lobes. In related models, particularly the spin-1/2 XXZ model on kagome (that is, J±±=0 and J±>0)31,32, the analogous lobes support a conventional VBS phase, which is evident in the diagonal structure factor:  , where
, where

If there is long-range order then  will scale with system size for at least one value of q. We also measure the bond-bond structure factor using a four-point correlation function.
will scale with system size for at least one value of q. We also measure the bond-bond structure factor using a four-point correlation function.

where  . Nearest neighbour sites iaα and jaα belong to bond α in a unit cell located at position ra. Again, if there is pair long-range order then
. Nearest neighbour sites iaα and jaα belong to bond α in a unit cell located at position ra. Again, if there is pair long-range order then  should scale with system size for at least one value of q, with which we define Bq=BBq/V.
should scale with system size for at least one value of q, with which we define Bq=BBq/V.
Figure 3 illustrates the various q-dependent structure factors for spin and bond order. These structure factors display diffuse peaks at various wave vectors, notably q=0, q=K=(2π/3,0), and symmetry-related momenta. Such peaks would indicate the presence of long-range order, should they sharpen, and survive in intensity in the infinite-size limit, where S/V would correspond to an order parameter squared. In Fig. 3d through Fig. 3f, we examine this through a standard finite-size scaling analysis, for several candidate peaks for each of the structure factors. Further scaling analysis, including larger system sizes, is presented and analysed in the light of perturbative arguments in the Supplementary Information (Supplementary Note 3 and Supplementary Figs 2 and 4). In each case, the QMC data indicates a scaling of each order parameter to zero in the limit V→∞. Note in particular, the largest value of Bq corresponds to q=0, which remains finite as V→∞, meaning that the bond expectation values  is finite in the lobes. This is expected as
is finite in the lobes. This is expected as  represents the kinetic energy of quantum fluctuations in the system, and thus it should be finite in all phases. More importantly, the data indicate that in the limit of V→∞ this quantity is the same on all bonds of the unit cell of the kagome lattice, meaning that there is no breaking of space-group symmetry (see Supplementary Note 4 and Supplementary Figs 5–7).
represents the kinetic energy of quantum fluctuations in the system, and thus it should be finite in all phases. More importantly, the data indicate that in the limit of V→∞ this quantity is the same on all bonds of the unit cell of the kagome lattice, meaning that there is no breaking of space-group symmetry (see Supplementary Note 4 and Supplementary Figs 5–7).
Off-diagonal nq (a), diagonal Sq (b), and bond BBq (c) structure factors inside the lobe for a system with Ns=24 × 24, h/Jz=0.8333, J±±/Jz=0.495 and T=Jz/48. In each panel, the colour scale represents the intensity of the structure factor. The corresponding finite-size scaling of candidate peaks at q values where local maxima occur in the structure factors n0 (d)(red hexagons), S0 and SK (e)(red triangles and green, respectively), and BK (f)(red squares). The error bars represent the one s.d. statistical uncertainty. Linear fits to the data in panels (d–f) are represented as blue dashed and black solid lines. The zero-momentum peak of BB0 in panel (c) has been removed. In each panel, the colour scales represent the intensity of the structure factor.
Finally, as the above data suggest the existence of a phase that is homogeneous, disordered and quantum-mechanically fluctuating at extremely low temperatures, one should also examine whether the energy for excitations out of this ground state is gapped or gapless. Although a direct measurement of the gap is not possible in this type of SSE QMC method, we can indirectly probe its existence by looking at the decay of real-space correlations. In Fig. 4, we compare the decay of single-particle correlations between the mz=±1/6 magnetization lobes and the adjacent FM ordered phase. For the system size studied, it is clear that correlations in the lobe are consistent with exponential decay, and therefore indicative of a gap. In contrast, in the FM phase the correlations quickly reach a finite value, indicating symmetry breaking (additional details about the nature the FM phase are discussed in Supplementary Figs 8–10 and Supplementary Note 5). Similarly, the diagonal part of the spin correlation function is consistent with exponential decay both in the lobes and in the FM phase (not illustrated).
The off-diagonal spin correlation function as a function of distance along the x direction for a system with Ns=24 × 24 and T=Jz/48 in the candidate spin liquid phase (blue squares) and in the ferromagnet (FM)(red triangles). The dashed line corresponds to a fit of the numerical data to the function  . The error bars represent the one s.d. statistical uncertainty.
. The error bars represent the one s.d. statistical uncertainty.
Thus, our QMC results have elucidated a phase diagram for our kagome pseudo-spin XYZ model (with J±=0), which contains a predominant FM phase, surrounding lobes of an exotic disordered mz=±1/6 magnetization phase. As our dual gauge theory (detailed in the Supplementary Note 1) indicates that these lobes may realize a QSL with an emergent Z2 gauge symmetry, it is clear that further simulation work should be carried out to address this hypothesis. To confirm the presence of a Z2 QSL, one requires evidence of either excitations consistent with this gauge structure (for example, magnetic spinons or non-magnetic visons at non-zero temperature) or a smoking gun such as the topological entanglement entropy40,41. Such evidence, although demonstrated in the past with SSE QMC42,43, is resource-intensive to obtain, requiring high numerical precision at very low temperatures, and thus outside of the scope of the present manuscript.
However, we also note that, due to the presence of only a discrete symmetry in our kagome XYZ model, an emergent Z2 structure is not strictly required by the Lieb-Schultz-Mattis-Hastings (LSMH) theorem44,45,46, which states that a system with half-odd-integer spin in the unit cell cannot have a gap and a unique ground state. In higher-symmetry Hamiltonians, the requirements of the LSMH theorem are satisfied in a gapped QSL phase by the topological degeneracy, which is a consequence of the emergent discrete gauge symmetry. For our Hamiltonian with a gapped QSL arising in a model with only global discrete symmetries, an emergent gauge structure is not required. Rather, it is possible that the groundstate is a quantum paramagnet. In contrast, other types of emergent gauge structure, topological order or other exotic phenomena are theoretically possible. Fortunately, the nature of this Hamiltonian, which is among the first to show a 2D QSL phase with only nearest-neighbour interactions, lends itself exceedingly well to study by sign-problem-free QMC simulations. We therefore expect a large number of studies in the near future will help elucidate the precise nature of this QSL phase.
Discussion
Through extensive quantum Monte Carlo simulations, we have studied a sign-problem-free model of frustrated quantum spins interacting on a two-dimensional kagome lattice. This model is descendent from a more general quantum XYZ Hamiltonian discussed by Huang, Chen and Hermele21, derived for the three-dimensional pyrochlore lattice, when subject to a magnetic field along the [111] crystallographic direction. For a large range of Hamiltonian parameters, the QMC data uncover an exotic disordered phase that breaks no symmetries, has strong quantum mechanical fluctuations and exponentially decaying correlations—a candidate gapped QSL phase. This discovery is consistent with an analytical dual gauge theory (detailed in the Supplementary Note 1), which indicates that, in the limit of small quantum fluctuations, the phase could be a 2D QSL with an emergent Z2 gauge symmetry.
Our work suggests a new experimental avenue to search for the highly coveted QSL phase in two dimensions. Previous efforts have focused largely on SU(2) Hamiltonians on kagome or triangular lattice materials6,7. In contrast, we propose to concentrate the search on the quantum spin ice pyrochlore materials, subject to an external field along the [111] direction. Such kagome ice phases have been identified in various materials in the past. A closer look at several quantum spin ice candidates is warranted, particularly in materials where strong quantum fluctuations are known to exist, such as Tb2Ti2O7, Yb2Ti2O7, Pr2Zr2O7 and Pr2Sn2O7. While Hamiltonians describing some of these materials may include additional interactions18 not considered in equation (1), our study highlights the importance of the of J±± term, which is present for instance in Yb2Ti2O7 (ref. 47), and promotes spinon pairing required in the formation of a Z2 spin liquid. As the phase found in this study has a gap, it is necessarily protected against any local perturbation as long as the effective energy scale of the perturbation is smaller than the gap, and thus it may still be realized even in the presence of additional perturbations. Other candidate materials where the Hamiltonian in equation (1) may be explicitly relevant include Nd2B2O7 (where B=Zr and Sn), rare earth spinels like CdEr2Se4, and Dy pyrochlores, though in the latter the effect of dipolar interactions need be considered21. In light of recent experiments48 that suggest the oft-studied classical spin ice state is only metastable in Dy2Ti2O7, it would seem prudent to re-examine the kagome ice state of this material using similar long-timescale techniques, to ascertain whether evidence of a QSL state may be present yet dynamically inhibited in the short-timescale studies performed to date.
Finally, we note that recent work by Glaetzle et al. have demonstrated that precisely our Hamiltonian (equation (1)) can be realized experimentally with cold alkali atoms stored in optical or magnetic trap arrays49. Such a proposal suggests that Quantum Kagome Ice may actually be realized in engineered systems of laser-dressed Rydberg atoms in the very near future.
Methods
Computational details
We developed a Stochastic Series Expansion34 (SSE) QMC algorithm in the global Sz basis designed to study the Hamiltonian equation (1) with J±=0 at finite temperature, using a 2+1-dimensional simulation cell. Within the SSE, the Hamiltonian was implemented with a triangular plaquette breakup36, which helps ergodicity in the regime where Jz/J±± is large. Using this Hamiltonian breakup, the standard SSE-directed loop equations35 were modified to include sampling of off-diagonal operators of the type  . The resulting algorithm is highly efficient, scaling linearly in the number of lattice sites V and the inverse temperature β. This scaling is modified to V2β in the cases where a full q-dependent structure factor measurement is required. The program was implemented in Fortran and verified by comparing results for small clusters with exact diagonalization data (See Supplementary Fig. 11 for an energy comparisons with ED and temperature convergence of the energy for larger system sizes). For each set of parameters in equation (1), the simulation typically requires 107 QMC steps, with ∼10% additional equilibration steps. The data presented in this paper required computational resources equivalent to 155 CPU core-years, run on a high-performance computing (HPC) cluster with Intel Xeon CPUs running at 2.83 GHz clock speed.
. The resulting algorithm is highly efficient, scaling linearly in the number of lattice sites V and the inverse temperature β. This scaling is modified to V2β in the cases where a full q-dependent structure factor measurement is required. The program was implemented in Fortran and verified by comparing results for small clusters with exact diagonalization data (See Supplementary Fig. 11 for an energy comparisons with ED and temperature convergence of the energy for larger system sizes). For each set of parameters in equation (1), the simulation typically requires 107 QMC steps, with ∼10% additional equilibration steps. The data presented in this paper required computational resources equivalent to 155 CPU core-years, run on a high-performance computing (HPC) cluster with Intel Xeon CPUs running at 2.83 GHz clock speed.
Additional information
How to cite this article: Carrasquilla, J. et al. A two-dimensional spin liquid in quantum kagome ice. Nat. Commun. 6:7421 doi: 10.1038/ncomms8421 (2015).
References
Anderson, P. W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198 (1987).
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: Physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Ioffe, L. B. et al. Topologically protected quantum bits using Josephson junction arrays. Nature 415, 503–506 (2002).
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
Yan, S., Huse, D. A. & White, S. R. Spin-liquid ground state of the S=1/2 Kagome Heisenberg antiferromagnet. Science 332, 1173–1176 (2011).
Pratt, F. L. et al. Magnetic and non-magnetic phases of a quantum spin liquid. Nature 471, 612–616 (2011).
Han, T.-H. et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 492, 406–410 (2012).
Gingras, M. J. P. & McClarty, P. A. Quantum spin ice: a search for gapless quantum spin liquids in pyrochlore magnets. Rep. Prog. Phys. 77, 056501 (2014).
Pauling, L. The structure and entropy of ice and of other crystals with some randomness of atomic arrangement. J. Am. Chem. Soc. 57, 2680–2684 (1935).
Bramwell, S. T. & Gingras, M. J. P. Spin ice state in frustrated magnetic pyrochlore materials. Science 294, 1495–1501 (2001).
Gingras, M. Spin Ice. Springer Series in Solid-State Sciences Vol. 164, 293-329 (Springer, 2011).
Hermele, M., Fisher, M. P. A. & Balents, L. Pyrochlore photons: The U(1) spin liquid in a S = 1/2 three-dimensional frustrated magnet. Phys. Rev. B 69, 064404 (2004).
Banerjee, A., Isakov, S. V., Damle, K. & Kim, Y. B. Unusual Liquid state of hard-core bosons on the pyrochlore lattice. Phys. Rev. Lett. 100, 047208 (2008).
Shannon, N., Sikora, O., Pollmann, F., Penc, K. & Fulde, P. Quantum ice: A Quantum Monte Carlo Study. Phys. Rev. Lett. 108, 067204 (2012).
Molavian, H. R., Gingras, M. J. P. & Canals, B. Dynamically induced frustration as a route to a quantum spin ice state in Tb2Ti2O7 via virtual crystal field excitations and quantum many-body effects. Phys. Rev. Lett. 98, 157204 (2007).
Kimura, K. et al. Quantum fluctuations in spin-ice-like Pr2Zr2O7 . Nat Commun 4, 1934 (2013).
Fennell, T. et al. Magnetoelastic excitations in the pyrochlore spin liquid Tb2Ti2O7 . Phys. Rev. Lett. 112, 017203 (2014).
Onoda, S. Effective quantum pseudospin-1/2 model for Yb pyrochlore oxides. J. Phys. 320, 012065 (2011).
Savary, L. & Balents, L. Coulombic quantum liquids in spin-1/2 pyrochlores. Phys. Rev. Lett. 108, 037202 (2012).
Lee, S., Onoda, S. & Balents, L. Generic quantum spin ice. Phys. Rev. B 86, 104412 (2012).
Huang, Y.-P., Chen, G. & Hermele, M. Quantum spin ices and topological phases from dipolar-octupolar doublets on the pyrochlore lattice. Phys. Rev. Lett. 112, 167203 (2014).
Matsuhira, K., Hiroi, Z., Tayama, T., Takagi, S. & Sakakibara, T. A new macroscopically degenerate ground state in the spin ice compound Dy2Ti2O7 under a magnetic field. J. Phys. Condens. Matter 14, L559–L565 (2002).
Moessner, R. & Sondhi, S. L. Theory of the [111] magnetization plateau in spin ice. Phys. Rev. B 68, 064411 (2003).
Isakov, S. V., Raman, K. S., Moessner, R. & Sondhi, S. L. Magnetization curve of spin ice in a [111] magnetic field. Phys. Rev. B 70, 104418 (2004).
Macdonald, A. J., Holdsworth, P. C. W. & Melko, R. G. Classical topological order in kagome ice. J. Phys. Condens. Matter 23, 164208 (2011).
Wills, A. S., Ballou, R. & Lacroix, C. Model of localized highly frustrated ferromagnetism: The kagomé spin ice. Phys. Rev. B 66, 144407 (2002).
Hiroi, Z., Matsuhira, K., Takagi, S., Tayama, T. & Sakakibara, T. Specific Heat of Kagomé Ice in the Pyrochlore Oxide Dy2Ti2O7. J. Phys. Soc. Jpn 72, 411–418 (2003).
Sakakibara, T., Tayama, T., Hiroi, Z., Matsuhira, K. & Takagi, S. Observation of a liquid-gas-type transition in the pyrochlore spin ice compound Dy2Ti2O7 in a magnetic field. Phys. Rev. Lett. 90, 207205 (2003).
Tabata, Y. et al. Kagomé ice state in the dipolar spin ice Dy2Ti2O7 . Phys. Rev. Lett. 97, 257205 (2006).
Molavian, H. R. & Gingras, M. J. P. Proposal for a [111] magnetization plateau in the spin liquid state of Tb2Ti2O7 . J. Phys. Condens. Matter 21, 172201 (2009).
Isakov, S. V., Wessel, S., Melko, R. G., Sengupta, K. & Kim, Y. B. Hard-core bosons on the Kagome lattice: valence-bond solids and their quantum melting. Phys. Rev. Lett. 97, 147202 (2006).
Damle, K. & Senthil, T. Spin nematics and magnetization plateau transition in anisotropic Kagome magnets. Phys. Rev. Lett. 97, 067202 (2006).
Fradkin, E. & Shenker, S. H. Phase diagrams of lattice gauge theories with Higgs fields. Phys. Rev. D 19, 3682–3697 (1979).
Sandvik, A. W. Stochastic series expansion method with operator-loop update. Phys. Rev. B 59, R14157–R14160 (1999).
Syljuåsen, O. F. & Sandvik, A. W. Quantum Monte Carlo with directed loops. Phys. Rev. E 66, 046701 (2002).
Melko, R. G. Simulations of quantum XXZ models on two-dimensional frustrated lattices. J. Phys. Condens. Matter 19, 145203 (2007).
Dorneich, A. & Troyer, M. Accessing the dynamics of large many-particle systems using the stochastic series expansion. Phys. Rev. E 64, 066701 (2001).
Penrose, O. & Onsager, L. Bose-Einstein condensation and liquid helium. Phys. Rev. 104, 576–584 (1956).
Giamarchi, T., Ruegg, C. & Tchernyshyov, O. Bose-Einstein condensation in magnetic insulators. Nat. Phys. 4, 198–204 (2008).
Kitaev, A. & Preskill, J. Topological Entanglement Entropy. Phys. Rev. Lett. 96, 110404 (2006).
Levin, M. & Wen, X.-G. Detecting topological order in a ground state wave function. Phys. Rev. Lett. 96, 110405 (2006).
Isakov, S. V., Hastings, M. B. & Melko, R. G. Topological entanglement entropy of a Bose-Hubbard spin liquid. Nat. Phys. 7, 772–775 (2011).
Tang, Y. & Sandvik, A. W. Method to characterize spinons as emergent elementary particles. Phys. Rev. Lett. 107, 157201 (2011).
Oshikawa, M. Commensurability, excitation gap, and topology in quantum many-particle systems on a periodic lattice. Phys. Rev. Lett. 84, 1535–1538 (2000).
Hastings, M. B. Lieb-Schultz-Mattis in higher dimensions. Phys. Rev. B 69, 104431 (2004).
Nachtergaele, B. & Sims, R. A multi-dimensional Lieb-Schultz-Mattis theorem. Commun. Math. Phys. 276, 437–472 (2007).
Ross, K., Savary, L., Gaulin, B. & Balents, L. Quantum excitations in quantum spin ice. Phys. Rev. X 1, 021002 (2011).
Pomaranski, D. et al. Absence of Pauling's residual entropy in thermally equilibrated Dy2Ti2O7 . Nat. Phys. 9, 353–356 (2013).
Glaetzle, A. W. et al. Frustrated Quantum Magnetism with Laser-Dressed Rydberg Atoms. Preprint at http://arxiv.org/abs/1410.3388 (2014).
Acknowledgements
We thank F. Becca, A. Burkov, L. Cincio, T. Senthil, M. Stoudenmire and W. Witczak-Krempa for enlightening discussions, and M. Gingras for critical reading of the manuscript. We are particularly indebted to Gang Chen for bringing the models discussed in ref. 21 to our attention and for stimulating discussions motivating this study. In addition, we are grateful to M. Heremele and A. Lauchli for emphasizing the role of perturbation theory. This research was supported by NSERC of Canada, the Perimeter Institute for Theoretical Physics, and the John Templeton Foundation. R.G.M. acknowledges support from a Canada Research Chair. Research at Perimeter Institute is supported through Industry Canada and by the Province of Ontario through the Ministry of Research & Innovation. Numerical simulations were carried out on the Shared Hierarchical Academic Research Computing Network (SHARCNET).
Author information
Authors and Affiliations
Contributions
J.C. and R.M. conceived the numerical strategy. J.C. designed and coded the algorithm, ran the computations, and performed the data analysis. Z.H. conceived the gauge theory mapping on the dual lattice. All the authors contributed to the interpretation of results, and the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-11, Supplementary Notes 1-5 and Supplementary References. (PDF 1899 kb)
Rights and permissions
About this article
Cite this article
Carrasquilla, J., Hao, Z. & Melko, R. A two-dimensional spin liquid in quantum kagome ice. Nat Commun 6, 7421 (2015). https://doi.org/10.1038/ncomms8421
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms8421
This article is cited by
-
Fragmentation in Frustrated Magnets: A Review
Journal of Low Temperature Physics (2020)
-
Evidence for dynamic kagome ice
Nature Communications (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.