Abstract
Systems driven out of equilibrium experience large fluctuations of the dissipated work. The same is true for wavefunction amplitudes in disordered systems close to the Anderson localization transition. In both cases, the probability distribution function is given by the large-deviation ansatz. Here we exploit the analogy between the statistics of work dissipated in a driven single-electron box and that of random multifractal wavefunction amplitudes, and uncover new relations that generalize the Jarzynski equality. We checked the new relations theoretically using the rate equations for sequential tunnelling of electrons and experimentally by measuring the dissipated work in a driven single-electron box and found a remarkable correspondence. The results represent an important universal feature of the work statistics in systems out of equilibrium and help to understand the nature of the symmetry of multifractal exponents in the theory of Anderson localization.
Similar content being viewed by others
Introduction
Unlike the adiabatic processes where the work W done on the system is equal to the difference in the free energy ΔF, the non-adiabatic drive protocols are associated with work that depends not only on the parameters of the system and details of the drive protocol but also experiences fluctuations relative to its average value1,2,3,4,5,6,7,8. Statistics of work can be described by the probability distribution function (PDF), Pw(W), and it is an important goal to find universal features in Pw(W) that remain unchanged within certain universality classes9. The best known relations of this kind are the Jarzynski equality10,11,12 and the Crooks relation13. The former one states that the exponent  averaged over repeated identical driving protocols is equal to 1, where T is the temperature of the single bath and kB is the Boltzmann constant. This necessarily implies that during some drive realizations the dissipated work W −ΔF must be negative in a naive (and wrong) contradiction with the second law, which only states that the average dissipated work remains positive. The Crooks relation
averaged over repeated identical driving protocols is equal to 1, where T is the temperature of the single bath and kB is the Boltzmann constant. This necessarily implies that during some drive realizations the dissipated work W −ΔF must be negative in a naive (and wrong) contradiction with the second law, which only states that the average dissipated work remains positive. The Crooks relation

concerns the PDFs of work in the direct (Pw(W)) and time-reversed ( ) processes. This relation has many important consequences (with the Jarzynski equality being one of them) and practical applications, for example, in the determination of free energy of folding proteins1,5.
) processes. This relation has many important consequences (with the Jarzynski equality being one of them) and practical applications, for example, in the determination of free energy of folding proteins1,5.
We use the Crooks relation to find a correspondence between statistics of work in a broad class of systems driven by time-reversal symmetric protocols and statistics of random multifractal wavefunctions in disordered quantum systems close to the Anderson localization transition14,15,16. The unifying principle of this correspondence17 is the so-called large-deviation principle18 according to which the PDF of a large variety of systems takes the form of the large-deviation ansatz (LDA),

where G(y) is a system-specific function. The LDA can be viewed as a generalization of the Central Limit Theorem of statistics according to which the sum S of a large number n of identically distributed independently fluctuating quantities sk has a limiting Gaussian distribution with the variance σ2∝n. Indeed, if we require that G(y) in equation (2) has a minimum, the expansion of this function near this minimum immediately results in the correct Gaussian PDF. The significance of the LDA is that it also describes the non-Gaussian tails of the distribution. Different realizations of LDA are characterized by different functions G(y) and different effective number n of independently fluctuating quantities. For example, in the discrete Markov process (or Markov chain) driving time t plays the role of large parameter n for steady-state distributions of dissipated work19 and heat20.
Critical eigenfunctions  (i=1, ... N) near the Anderson localization transition and in certain random matrix ensembles have multifractal statistics14,15,16. A characteristic feature of such statistics is that the eigenfunction amplitude
(i=1, ... N) near the Anderson localization transition and in certain random matrix ensembles have multifractal statistics14,15,16. A characteristic feature of such statistics is that the eigenfunction amplitude  takes a broad set of values (at different sites i or in different realizations of disorder) that scale like
takes a broad set of values (at different sites i or in different realizations of disorder) that scale like  (α>0) with the total number of sites N in a disordered tight-binding lattice (or the matrix size). The number of sites on a lattice where scaling is characterized by a certain α is M∼Nf(α) , where f(α) is known as the spectrum of fractal dimensions. Where α is taking only one single value α0, the set of ‘occupied’ sites on the d-dimensional lattice would be a fractal with the Hausdorff dimension dh=d·f(α0). Multifractality implies that there is a range of possible values of α with the corresponding range of fractal dimensions f(α). In the language of LDA, this implies that PDF of the amplitude
(α>0) with the total number of sites N in a disordered tight-binding lattice (or the matrix size). The number of sites on a lattice where scaling is characterized by a certain α is M∼Nf(α) , where f(α) is known as the spectrum of fractal dimensions. Where α is taking only one single value α0, the set of ‘occupied’ sites on the d-dimensional lattice would be a fractal with the Hausdorff dimension dh=d·f(α0). Multifractality implies that there is a range of possible values of α with the corresponding range of fractal dimensions f(α). In the language of LDA, this implies that PDF of the amplitude  has a form equation (2) with
has a form equation (2) with  and n=ln N. The function G(y) is related with the multifractality spectrum f(α) as G(y)=1−f(1+y)14. It depends on parameters of the system such as the dimensionality or the bandwidth of the random matrix ensemble, and has a non-trivial limit at N→∞. There is a remarkable symmetry14,17,21,
and n=ln N. The function G(y) is related with the multifractality spectrum f(α) as G(y)=1−f(1+y)14. It depends on parameters of the system such as the dimensionality or the bandwidth of the random matrix ensemble, and has a non-trivial limit at N→∞. There is a remarkable symmetry14,17,21,

whose physical origin is perhaps deeper than a current understanding22 based on ‘full chaotization’ of particle dynamics in a random potential, which leads to the homogeneous distribution of the scattering phase off the disordered system.
An important observation17 with potentially very far-reaching consequences is that within the LDA the symmetry; equation (3) is equivalent to the Crooks-like relation,

In this work, we formulate a generalization, equation (7), of the Jarzynski equality for the work-generating function. This generalization has been proven theoretically by a stochastic calculus using the rate equations and experimentally for a driven single-electron box (SEB) in the Coulomb blockade regime.
Results
The large-deviation parameter and the temperature
To formulate a dictionary between the statistics of work in driven systems and that of random multifractal eigenfunctions, we compare equations (1) and (4) assuming that the drive protocol in equation (1) is time-reversal symmetric, therefore  . Using this comparison and the definition of S and n for multifractal wavefunctions, we obtain
. Using this comparison and the definition of S and n for multifractal wavefunctions, we obtain

where the subscript w stands for the distribution of work fluctuations. To determine the yet undefined parameter nw, we use the following heuristic argument based on the above analogy. We note that for a normalized eigenfunction on a lattice obeying  we have
we have  . This means that y≥−1. A similar restriction for yw implies (W−ΔF)/kBT ≥ − nw, that is
. This means that y≥−1. A similar restriction for yw implies (W−ΔF)/kBT ≥ − nw, that is

where (−E0) is the lower bound of the dissipated work. This result for the large-deviation parameter nw can be proven by a usual stochastic approach (see equation (15) in the Supplementary Note 1) for the SEB governed by rate equations obeying detailed balance. However, we believe that it is valid generically for all driven systems with the dissipated work bounded from below. Thus the effective number (equation (6)) of independent random variables in such driven systems is inversely proportional to temperature T and is easily controllable experimentally. This result is crucially important for experimental verification of our extension of the Jarzynski equality.
Work-generating function and extension of the Jarzynski equality
With the established physical meaning of nw, the analogy between the work distribution in driven systems and the multifractal statistics of random eigenfunctions becomes complete. It is illustrated in Figs 1 and 2.
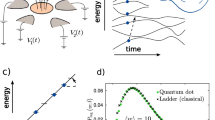
(a) Distribution of the measured normalized dissipated work (W−ΔF)/E0 on the logarithmic scale. The width of the distributions increases with increasing drive frequency f=1 (red), 2 (green) and 4 Hz (violet) at temperature T=214 mK. (b) Multifractality spectrum f(α) of critical eigenfunctions in disordered systems close to the Anderson localization transition versus normalized logarithm of wavefunction intensity  for the power-law random banded matrix model with the bandwidth b=0.1, 0.3, 1, 4 (adapted with permission from ref. 21. Copyrighted by the American Physical Society). This parameter is known to mimic the dimensionality of space in which the Anderson transition happens: b→0 corresponds to the limit of infinite dimensionality d→∞, or the Bethe lattice limit, while b→∞ corresponds to d=2+ɛ, where ɛ →+0. In both a and b, solid and dashed lines correspond to G(y), G(−y)−y and f(α), f(2−α)+α−1, respectively, to demonstrate the symmetry (equation (3)). (c) Evolution of distribution of the normalized dissipated work (W−ΔF)/E0 on the logarithmic scale with decreasing drive frequency f in a SEB with a superconducting external electrode for experimental system parameters and T=214 mK obtained theoretically from the rate equations (equations (3) and (4) in the Supplementary Note 1). The width of the distributions decreases with decreasing driving frequency f (from red to violet curve). The similar calculations for the SEB with the normal electrode give
for the power-law random banded matrix model with the bandwidth b=0.1, 0.3, 1, 4 (adapted with permission from ref. 21. Copyrighted by the American Physical Society). This parameter is known to mimic the dimensionality of space in which the Anderson transition happens: b→0 corresponds to the limit of infinite dimensionality d→∞, or the Bethe lattice limit, while b→∞ corresponds to d=2+ɛ, where ɛ →+0. In both a and b, solid and dashed lines correspond to G(y), G(−y)−y and f(α), f(2−α)+α−1, respectively, to demonstrate the symmetry (equation (3)). (c) Evolution of distribution of the normalized dissipated work (W−ΔF)/E0 on the logarithmic scale with decreasing drive frequency f in a SEB with a superconducting external electrode for experimental system parameters and T=214 mK obtained theoretically from the rate equations (equations (3) and (4) in the Supplementary Note 1). The width of the distributions decreases with decreasing driving frequency f (from red to violet curve). The similar calculations for the SEB with the normal electrode give  , where τ0 is the characteristic relaxation time of the circuit. Thus an effective bandwidth b of the equivalent random matrix theory depends on the equivalent size of the matrix N=exp(E0/kBT). While the limit T→0 always corresponds to the limit b→0, the limit f→0 at a fixed T corresponds to the adiabatic limit b→∞.
, where τ0 is the characteristic relaxation time of the circuit. Thus an effective bandwidth b of the equivalent random matrix theory depends on the equivalent size of the matrix N=exp(E0/kBT). While the limit T→0 always corresponds to the limit b→0, the limit f→0 at a fixed T corresponds to the adiabatic limit b→∞.
 for dissipated work and multifractal critical exponents Δq.
for dissipated work and multifractal critical exponents Δq.(a) The measured function  in equation (7) at drive frequencies f=1 (red), 2 (green) and 4 Hz (violet) and temperature T=214 mK. (Inset) A plot of the exponent of the dissipative work
in equation (7) at drive frequencies f=1 (red), 2 (green) and 4 Hz (violet) and temperature T=214 mK. (Inset) A plot of the exponent of the dissipative work  versus the drive realization number j at a drive frequency f=1 Hz and temperature T=214 mK. In most of the drives the exponent is smaller than 1, which corresponds to W>ΔF, as the second law requires for averages. However, there are rare events seen as high spikes when ΔF−W>kBT. (b) Multifractal exponents Δq for the same model and parameters as in Fig. 1b (adapted with permission from ref. 21. Copyrighted by the American Physical Society). In both a and b small difference between Δq (solid lines) and Δ1 − q (dashed lines) violating the symmetry (equation (8)) is due to experimental (in a) or numerical (in b) errors. (Bottom inset) A plot of a typical amplitude
versus the drive realization number j at a drive frequency f=1 Hz and temperature T=214 mK. In most of the drives the exponent is smaller than 1, which corresponds to W>ΔF, as the second law requires for averages. However, there are rare events seen as high spikes when ΔF−W>kBT. (b) Multifractal exponents Δq for the same model and parameters as in Fig. 1b (adapted with permission from ref. 21. Copyrighted by the American Physical Society). In both a and b small difference between Δq (solid lines) and Δ1 − q (dashed lines) violating the symmetry (equation (8)) is due to experimental (in a) or numerical (in b) errors. (Bottom inset) A plot of a typical amplitude  of the critical wavefunction in a two-dimensional lattice with N sites cut at a certain level
of the critical wavefunction in a two-dimensional lattice with N sites cut at a certain level  (adapted with permission from ref. 39. Copyrighted by the American Physical Society). (Top inset) The map of the region in space where
(adapted with permission from ref. 39. Copyrighted by the American Physical Society). (Top inset) The map of the region in space where  is a fractal of the Haussdorf dimension dh(α)=2f(α)<2. Multifractality implies a dependence of dh on α, or on the cutoff level N−α (adapted with permission from ref. 40. Copyrighted by the American Physical Society).
is a fractal of the Haussdorf dimension dh(α)=2f(α)<2. Multifractality implies a dependence of dh on α, or on the cutoff level N−α (adapted with permission from ref. 40. Copyrighted by the American Physical Society).
A remarkable property of the LDA (equation (2)) is that the average of  is an exponential function of n≫1, where
is an exponential function of n≫1, where  18,19. Given that n=lnN, this implies a power-law scaling with N of the moments
18,19. Given that n=lnN, this implies a power-law scaling with N of the moments  (with
(with  ) of random wavefunctions near the critical point of the Anderson localization transition. When applied to the statistics of work, the exponential dependence on nw=E0/kBT results in the following relation for the work-generating function
) of random wavefunctions near the critical point of the Anderson localization transition. When applied to the statistics of work, the exponential dependence on nw=E0/kBT results in the following relation for the work-generating function  :
:

where the limit  is independent of temperature. Equation (7) is the main theoretical result of our work, where we claim that the logarithm of the work-generating function is linear in E0/kBT≫1, with
is independent of temperature. Equation (7) is the main theoretical result of our work, where we claim that the logarithm of the work-generating function is linear in E0/kBT≫1, with  being a non-trivial function of a real q. It generalizes the Jarzynski equality, which corresponds to q=1 and
being a non-trivial function of a real q. It generalizes the Jarzynski equality, which corresponds to q=1 and  . Apparently, we have also
. Apparently, we have also  . One can easily show using equation (3) and the definition of
. One can easily show using equation (3) and the definition of  that the symmetry
that the symmetry

holds both for  and for
and for  . This symmetry has its counterpart for the critical exponents Δq that determine the scaling with N of the moments of random critical wavefunctions. The limit
. This symmetry has its counterpart for the critical exponents Δq that determine the scaling with N of the moments of random critical wavefunctions. The limit  of
of  at E0/kBT→∞ (at a fixed drive frequency f) is expected to be robust to changing the details of the driven system and the drive protocol. For a driven two-level system, described by rate equations (equations (3) and (4)) in the Supplementary Note 1) and obeying detailed balance
at E0/kBT→∞ (at a fixed drive frequency f) is expected to be robust to changing the details of the driven system and the drive protocol. For a driven two-level system, described by rate equations (equations (3) and (4)) in the Supplementary Note 1) and obeying detailed balance  for the up (down) transition rates Γ+ (Γ−), standard stochastic dynamics calculus confirms the main result equations (6) and (7), with
for the up (down) transition rates Γ+ (Γ−), standard stochastic dynamics calculus confirms the main result equations (6) and (7), with  having always the same asymptotic behaviour
having always the same asymptotic behaviour  at large enough |q|≫qc (see equation (18) in the Supplementary Note 1). This form of
at large enough |q|≫qc (see equation (18) in the Supplementary Note 1). This form of  corresponds to the limit of infinite dimensions, or the Bethe lattice limit23, in the problem of the random critical wavefunctions. Note that the universal behaviour of
corresponds to the limit of infinite dimensions, or the Bethe lattice limit23, in the problem of the random critical wavefunctions. Note that the universal behaviour of  (and the corresponding behaviour of Pw(W)) is reached only in the limit T→0, with all other parameters of the system and drive being fixed. If, however, the temperature is low but fixed, then there always exists a sufficiently low drive frequency f such that the dissipated work distribution tends to a δ-function, as the adiabatic limit requires24. For a SEB with a superconducting electrode, the range of such frequencies could be extremely low at temperatures kBT<<ΔS, with ΔS being a superconducting gap in the island (see Fig. 1c).
(and the corresponding behaviour of Pw(W)) is reached only in the limit T→0, with all other parameters of the system and drive being fixed. If, however, the temperature is low but fixed, then there always exists a sufficiently low drive frequency f such that the dissipated work distribution tends to a δ-function, as the adiabatic limit requires24. For a SEB with a superconducting electrode, the range of such frequencies could be extremely low at temperatures kBT<<ΔS, with ΔS being a superconducting gap in the island (see Fig. 1c).
Experimental verification for a SEB
The general theory above can be applied to a driven SEB, which is a small metallic island connected to an external electrode with a tunnel junction. The free electrons on the SEB island and the electrode form a particle bath, assumed to be at thermal equilibrium at temperature T (refs 6, 25). A standard rate equation approach26,27, which is essentially classical and based on the picture of sequential tunnelling of electrons, confirms our main result (equation (7)) and the symmetry (equation (8)) (see Supplementary Notes 1 and 2). This theory gives a linear in T−1 low-temperature behaviour of the cumulant generating function (left-hand side of equation (7)), as shown in Fig. 3a,b. We consider two different cases as examples belonging to different universality classes marked by a drastically different dependence of the tunnelling rate Γ+(U) on the drive voltage U≫kBT: a SEB with normal island and (a) a superconducting external electrode ( , ΔS>U) or (b) a normal external electrode (
, ΔS>U) or (b) a normal external electrode ( ). The evolution of
). The evolution of  with temperature in both cases is shown in Fig. 4. The limiting
with temperature in both cases is shown in Fig. 4. The limiting  appears to be of triangular shape in case (a), and of trapezoidal shape in case (b).
appears to be of triangular shape in case (a), and of trapezoidal shape in case (b).
In a and b, the theoretical T−1 dependence obtained from the rate equations for a SEB with (a) a superconducting and (b) a normal external electrode is shown. (c) Demonstration of the experimental test of this dependence. In all panels the dependencies become linear at large values of T−1. The dashed (solid) lines correspond to the pairs of moments {q,1−q} related by symmetry. The curves from bottom to top correspond to {4, −3}, {3, −2}, {2, −1}, {1,0} and  . In c, the dashed (solid) lines of the same colour are linear fits of the experimental data shown by open (solid) circles corresponding to q (1−q). (Inset) The linear in T extrapolation for the function
. In c, the dashed (solid) lines of the same colour are linear fits of the experimental data shown by open (solid) circles corresponding to q (1−q). (Inset) The linear in T extrapolation for the function  . The notations are the same as in c.
. The notations are the same as in c.
 with decreasing temperature T in a single-electron box.
with decreasing temperature T in a single-electron box.(a,b) The theoretical evolution for a SEB with (a) a superconducting external electrode for ΔS=EC and (b) a normal external electrode obtained from the rate equations. The limiting  is of (a) triangular, (b) trapezoidal form. Experimental data are shown in c and d. (c) Experimentally obtained
is of (a) triangular, (b) trapezoidal form. Experimental data are shown in c and d. (c) Experimentally obtained  for temperatures T=111, 123, 133, 144, 153 and 175 mK are plotted as functions of q (coloured solid lines). The solid black curve
for temperatures T=111, 123, 133, 144, 153 and 175 mK are plotted as functions of q (coloured solid lines). The solid black curve  is obtained by linear in T extrapolation of the experimental data to zero temperature. The thin grey curves and dotted arrows demonstrate the linear extrapolation. (d) The verification of the symmetry (equation (8)). Here the dashed grey curve shows
is obtained by linear in T extrapolation of the experimental data to zero temperature. The thin grey curves and dotted arrows demonstrate the linear extrapolation. (d) The verification of the symmetry (equation (8)). Here the dashed grey curve shows  , the other notations are the same as in c.
, the other notations are the same as in c.
The main quantum effects, which are beyond the rate equation approach, are the elastic co-tunnelling28 and the Andreev tunnelling29. Estimations show (see equation (3) and the Supplementary Note 3) that for SEB at our experimental conditions, they may become relevant at low temperatures T<T*∼60 mK. We believe that these effects merely renormalize the parameter E0 and the function  and do not change the 1/T behaviour in equation (7). Further investigations are necessary to check the validity of this conjecture.
and do not change the 1/T behaviour in equation (7). Further investigations are necessary to check the validity of this conjecture.
For an experimental verification of our main result (equation (7)) and the symmetry (equation (8)), we use a SEB formed by two metallic islands, of which one is normal and the other one is superconducting with energy gap ΔS. As a two-island SEB is only capacitively coupled to the environment, it is less influenced by external noise from higher temperature stages of the set-up. Otherwise its behaviour is identical to a normal one-island SEB with a superconducting ‘external electrode’. The measured structure is described in refs 6, 30, 31. We used aluminium and copper as a superconductor and a normal metal, respectively, and apply magnetic field to increase the tunnelling rates through the junction by suppressing the gap ΔS, see the Supplementary Note 4 for details. The Hamiltonian H(n,ng)=EC(n2−2n ng) of the SEB consists of the charging energy of the island with an integer number of excess electrons n and the interaction with the source of the gate voltage Vg controlling the gate charge ng=CgVg/e through the capacitance Cg. The energy required to charge the island with a single electron −e is EC=e2/2CΣ, where CΣ is the total capacitance of the island. In this experiment, we apply a sinusoidal modulation  and consider a monotonous segment of ng(t) from 0 to 1 as a single realization of the process 0<t<(2f)−1. We focus on the large Coulomb energy limit EC≫kBT, in which n is restricted to two values, n=0 and n=1. In this case, the dissipated work is determined from the trajectory of n(t) by24,32
and consider a monotonous segment of ng(t) from 0 to 1 as a single realization of the process 0<t<(2f)−1. We focus on the large Coulomb energy limit EC≫kBT, in which n is restricted to two values, n=0 and n=1. In this case, the dissipated work is determined from the trajectory of n(t) by24,32

Like in the textbook example of a moving piston where the volume V(t) of the gas is controlled deterministically and the pressure p(t) experiences fluctuations due to collisions of gas atoms with the piston, the gate voltage ng(t) is a deterministic function, whereas n(t) experiences telegraph fluctuations. These fluctuations are detected by a nearby charge-sensitive single-electron transistor. The dissipated work is computed from equation (9) and its statistics over repeated identical driving protocols is studied. Here the lower bound −E0 of the dissipated work is determined by the Coulomb energy E0=EC.
The experimental PDFs of work for few different drive frequencies are presented in Fig. 1. This plot demonstrates the dependence of the PDF on the frequency, which is reminiscent of the dependence on the bandwidth b of the corresponding PDF for random multifractal wavefunctions for the power-law banded random matrices14. Using this PDF one can compute the qth moments of  for different values of the parameter q and find the function
for different values of the parameter q and find the function  from equation (7) (see Fig. 2). In both figures the charging energy of the SEB determining the dissipated work equation (9) is EC=167±4 μeV, while the bath temperature is T=214 mK. The drive frequencies are indicated in the figures.
from equation (7) (see Fig. 2). In both figures the charging energy of the SEB determining the dissipated work equation (9) is EC=167±4 μeV, while the bath temperature is T=214 mK. The drive frequencies are indicated in the figures.
Next, we check experimentally the linear in E0/kBT low-temperature dependence in equation (7) and the symmetry of equation (8). The results are presented in Fig. 3c. The corresponding theoretical curves are given in Fig. 3a,b. Note a good linearity of experimental data for the negative q (full circles, solid lines) and a much larger scatter of it (open circles) for the large positive q, which corresponds to rare events with W−ΔF<0. The linear in T evolution of  is demonstrated experimentally in Fig. 4c. Its counterpart for the random eigenfunction problem is the evolution with the system size N linear in 1/lnN, which was used recently in ref. 23 to find the spectrum of fractal dimensions f(α) extrapolated to the infinite system size. Similarly to this work, the limiting function
is demonstrated experimentally in Fig. 4c. Its counterpart for the random eigenfunction problem is the evolution with the system size N linear in 1/lnN, which was used recently in ref. 23 to find the spectrum of fractal dimensions f(α) extrapolated to the infinite system size. Similarly to this work, the limiting function  is obtained by the linear in T extrapolation to T→0 (see the inset in Fig. 3c). In both figures, the charging energy is EC=111±4 μeV, the drive frequency is f=4 Hz, while the temperatures are indicated in the figures. The estimated33,34,35 value of the superconducting energy gap ΔS=96±11 μeV in applied magnetic field is rather close to EC in this case. The corresponding extrapolated function
is obtained by the linear in T extrapolation to T→0 (see the inset in Fig. 3c). In both figures, the charging energy is EC=111±4 μeV, the drive frequency is f=4 Hz, while the temperatures are indicated in the figures. The estimated33,34,35 value of the superconducting energy gap ΔS=96±11 μeV in applied magnetic field is rather close to EC in this case. The corresponding extrapolated function  shown in Fig. 4c is close to the triangular form obtained theoretically from the rate equations in the ideal case ΔS=EC and shown in Fig. 4a, albeit it is somewhat rounded on the top following a trend towards the trapezoidal form shown in Fig. 4b. The asymptotic behaviour of the extrapolated function
shown in Fig. 4c is close to the triangular form obtained theoretically from the rate equations in the ideal case ΔS=EC and shown in Fig. 4a, albeit it is somewhat rounded on the top following a trend towards the trapezoidal form shown in Fig. 4b. The asymptotic behaviour of the extrapolated function  at q>1 or q<0 is close to the theoretically predicted asymptotics
at q>1 or q<0 is close to the theoretically predicted asymptotics  , linear in q with unit slope, supporting the linear in T extrapolation.
, linear in q with unit slope, supporting the linear in T extrapolation.
Discussion
In conclusion, we have shown that the analogy between the statistics of random critical wavefunctions and that of the work dissipated in driven systems is very suggestive. Its predictions are fully confirmed theoretically and experimentally by studying stochastic dynamics in a driven SEB described by rate equations obeying detailed balance. Thus one of the most difficult problems in quantum mechanics of disordered systems turns out to be analogous to one of the simplest problem in classical stochastic Markovian dynamics. In particular, the physical origin of the symmetry (equation (8)) is somewhat unclear in the problem of Anderson localization (but see ref. 22). At the same time, the corresponding symmetry for driven systems is a consequence of the Crooks relation or, equivalently, of detailed balance for rate equations. This might suggest that there would be a stochastic description for the critical random eigenfunction problem by an equivalent Markovian process with detailed balance. One can see a remote analogy of such correspondence in the Schramm–Loewner evolution, which maps fractal phase boundaries in two-dimensional critical systems onto a simple random walk on a line36,37,38.
Additional information
How to cite this article: Khaymovich, I. M. et al. Multifractality of random eigenfunctions and generalization of Jarzynski equality. Nat. Commun. 6:7010 doi: 10.1038/ncomms8010 (2015).
References
Liphardt, J., Dumont, S., Smith, S. B., Tinoco, I. Jr & Bustamante, C. Equilibrium information from nonequilibrium measurements in an experimental test of Jarzynski's equality. Science 296, 1832–1835 (2002).
Wang, G. M., Sevick, E. M., Mittag, E., Searles, D. J. & Evans, D. J. Experimental demonstration of violations of the second law of thermodynamics for small systems and short time scales. Phys. Rev. Lett. 89, 050601 (2002).
Collin, D. et al. Verification of the Crooks fluctuation theorem and recovery of RNA folding free energies. Nature 437, 231–234 (2005).
Blickle, V., Speck, T., Helden, L., Seifert, U. & Bechinger, C. Thermodynamics of a colloidal particle in a time-dependent nonharmonic potential. Phys. Rev. Lett. 96, 070603 (2006).
Junier, I., Mossa, A., Manosas, M. & Ritort, F. Recovery of free energy branches in single molecule experiments. Phys. Rev. Lett. 102, 070602 (2009).
Saira, O.-P. et al. Test of the Jarzynski and Crooks fluctuation relations in an electronic system. Phys. Rev. Lett. 109, 180601 (2012).
Utsumi, Y. et al. Bidirectional single-electron counting and the fluctuation theorem. Phys. Rev. B 81, 125331 (2010).
Küng, B. et al. Irreversibility on the level of single-electron tunneling. Phys. Rev. X 2, 011001 (2012).
Polkovnikov, A., Sengupta, K., Silva, A. & Vengalattore, M. Colloquium: nonequilibrium dynamics of closed interacting quantum systems. Rev. Mod. Phys. 83, 863 (2011).
Bochkov, G. N. & Kuzovlev, I. E. General theory of thermal fluctuations in nonlinear systems. Sov. Phys. JETP 45, 125 (1977).
Bochkov, G. N. & Kuzovlev, I. E. Nonlinear fluctuation-dissipation relations and stochastic models in nonequilibrium thermodynamics: I. generalized fluctuation-dissipation theorem. Physica A106, 443 (1981).
Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 78, 2690–2693 (1997).
Crooks, G. E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 60, 2721–2726 (1999).
Evers, F. & Mirlin, A. D. Anderson transitions. Rev. Mod. Phys. 80, 1355 (2008).
Kravtsov, V. E. & Muttalib, K. A. New class of random matrix ensembles with multifractal eigenvectors. Phys. Rev. Lett. 79, 1913 (1997).
Kravtsov, V. E. in: The Oxford Handbook of Random Matrix Theory eds Akemann G., Baik J., Di Francesco P. 250–269Oxford Univ. Press (2011).
Monthus, C., Berche, B. & Chatelain, C. Symmetry relations for multifractal spectra at random critical points. J. Stat. Mech. P12002 (2009).
Touchette, H. The large deviation approach to statistical mechanics. Phys. Rep. 478, 1 (2009).
Verley, G., Van den Broeck, C. & Esposito, M. Modulated two-level system: exact work statistics. Phys. Rev. E 88, 032137 (2013).
Fogedby, H. C. & Imparato, A. A bound particle coupled to two thermostats. J. Stat. Mech. P05015 (2011).
Mirlin, A. D., Fyodorov, Y. V., Mildenberger, A. & Evers, F. Exact relations between multifractal exponents at the Anderson transition. Phys. Rev. Lett. 97, 046803 (2006).
Fyodorov, Y. V. & Savin, D. V. Statistics of impedance, local density of states, and reflection in quantum chaotic systems with absorption. JETP Lett. 80, 725–729 (2004).
De Luca, A., Altshuler, B. L., Kravtsov, V. E. & Scardicchio, A. Anderson localization on the Bethe lattice: nonergodicity of extended states. Phys. Rev. Lett. 113, 046806 (2014).
Averin, D. V. & Pekola, J. P. Statistics of the dissipated energy in driven single-electron transitions. Europhys. Lett. 96, 67004 (2011).
Koski, J. V. et al. Distribution of entropy production in a single-electron box. Nat. Phys. 9, 644–648 (2013).
Averin, D. V. & Likharev, K. K. Coulomb blockade of single-electron tunneling, and coherent oscillations in small tunnel-junctions. J. Low Temp. Phys. 62, 345–373 (1986).
Likharev, K. K. Single-electron transistors: electrostatic analogs of the DC SQUIDS. IEEE Trans. Magn. 23, 1142–1145 (1987).
Averin, D. V. & Nazarov, Y. u. V. Virtual electron diffusion during quantum tunneling of the electric charge. Phys. Rev. Lett. 65, 2446–2449 (1990).
Averin, D. V. & Pekola, J. P. Nonadiabatic charge pumping in a hybrid single-electron transistor. Phys. Rev. Lett. 101, 066801 (2008).
Koski, J. V., Maisi, V. F., Sagawa, T. & Pekola, J. P. Experimental observation of the role of mutual information in the nonequilibrium dynamics of a Maxwell demon. Phys. Rev. Lett. 113, 030601 (2014).
Koski, J. V., Maisi, V. F., Pekola, J. P. & Averin, D. V. Experimental realization of a Szilard engine with a single electron. Proc. Natl Acad. Sci. USA 111, 13786–13789 (2014).
Pekola, J. P. & Saira, O.-P. Work, free energy and dissipation in voltage driven single-electron transitions. J. Low Temp. Phys. 169, 70–76 (2012).
Skalski, S., Betbeder-Matibet, O. & Weiss, P. R. Properties of superconducting alloys containing paramagnetic impurities. Phys. Rev 136, A1500–A1518 (1964).
Maki, K. & Fulde, P. Equivalence of different pair-breaking mechanisms in superonductors. Phys. Rev. 140, A1586–A1592 (1965).
Anthore, A., Pothier, H. & Esteve, D. Density of states in a superconductor carrying a supercurrent. Phys. Rev. Lett. 90, 127001 (2003).
Schramm, O. Scaling limits of loop-erased random walks and uniform spanning trees. Isr. J. Math. 118, 221–288 (2000).
Lawler, G. F. Conformally invariant processes in the plane American Mathematical Society (2005).
Werner, W. in Lecture Notes in Mathematics 1840, Springer (2004).
Obuse, H. & Yakubo, K. Critical level statistics and anomalously localized states at the Anderson transition. Phys. Rev. B 71, 035102 (2005).
Cuevas, E. & Kravtsov, V. E. Two-eigenfunction correlation in a multifractal metal and insulator. Phys. Rev. B 76, 235119 (2007).
Acknowledgements
We thank Professor F. Hekking, Professor B.L. Altshuler for useful discussions and Professor A.S. Mel'nikov for advice in improving the manuscript. This work has been supported in part by the Academy of Finland (projects nos 250280 and 272218), the European Union Seventh Framework Programme INFERNOS (FP7/2007–2013) under grant agreement no. 308850, the Russian president foundation (project no. SP-1491.2012.5) and the Väisälä Foundation. V.E.K. acknowledges the hospitality of LPTMS of University of Paris Sud at Orsay and support under the CNRS grant ANR-11-IDEX-0003-02 Labex PALM, project MultiScreenGlass. We acknowledge the availability of the facilities and technical support by Otaniemi research infrastructure for Micro and Nanotechnologies (OtaNano).
Author information
Authors and Affiliations
Contributions
J.V.K., O.-P.S. and J.P.P. conceived and designed the experiments. J.V.K. and O.-P.S. performed the experiments. I.M.K., J.V.K. and O.-P.S. analysed the data. I.M.K., V.E.K. and J.P.P. contributed with materials/analysis tools. I.M.K., J.V.K., V.E.K. and J.P.P. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Notes 1-4 and Supplementary References (PDF 240 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Khaymovich, I., Koski, J., Saira, OP. et al. Multifractality of random eigenfunctions and generalization of Jarzynski equality. Nat Commun 6, 7010 (2015). https://doi.org/10.1038/ncomms8010
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms8010
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.