Abstract
SrCu2(BO3)2 is the archetypal quantum magnet with a gapped dimer-singlet ground state and triplon excitations. It serves as an excellent realization of the Shastry–Sutherland model, up to small anisotropies arising from Dzyaloshinskii–Moriya interactions. Here we demonstrate that these anisotropies, in fact, give rise to topological character in the triplon band structure. The triplons form a new kind of Dirac cone with three bands touching at a single point, a spin-1 generalization of graphene. An applied magnetic field opens band gaps resulting in topological bands with Chern numbers ±2. SrCu2(BO3)2 thus provides a magnetic analogue of the integer quantum Hall effect and supports topologically protected edge modes. At a threshold value of the magnetic field set by the Dzyaloshinskii–Moriya interactions, the three triplon bands touch once again in a spin-1 Dirac cone, and lose their topological character. We predict a strong thermal Hall signature in the topological regime.
Similar content being viewed by others
Introduction
Topological phases of bosons have steadily gained interest, driven by the goal of realizing protected edge states that do not suffer from dissipation. As bosonic carriers (phonons, magnons and so on) are electrically neutral, they are weakly interacting and show good coherent transport. As a first step in this direction, analogues of the integer quantum Hall effect have been proposed using photons1,2,3,4, magnons5,6,7,8,9, phonons10,11,12 and skyrmionic textures13, with the thermal Hall effect14 as the experimental probe of choice. It would be very interesting to observe this phenomenon in quantum magnets, where the quantization of spin produces a new class of bosonic excitations called triplons.
The archetypal quantum magnet is SrCu2(BO3)2, a layered material consisting of Cu S=1/2 moments arranged in orthogonal dimers15,16. To a very good approximation, this arrangement conforms to the Shastry–Sutherland model17,18. Low-energy excitations correspond to breaking a singlet to form a triplet. Such excitations are called triplons and can be thought of as spin-1 bosonic particles19. Indeed, triplons undergo Bose condensation in many systems20,21,22. If SrCu2(BO3)2 were an exact realization of the Shastry–Sutherland model, the triplons would be local excitations forming a threefold-degenerate flat band23. However, electron spin resonance (ESR)24, infrared absorption25, neutron scattering26 and Raman scattering27 measurements show a weak dispersion that has been attributed to small Dzyaloshinskii–Moriya (DM) anisotropies28,29,30. Nuclear magnetic resonance measurements also support the presence of DM couplings31.
Here, we show that DM couplings give rise to topological character in the triplon energy spectrum of SrCu2(BO3)2. A small magnetic field suffices to induce phases with Chern bands and topologically protected edge states. As triplons carry energy but no electrical charge, we predict a thermal Hall effect of triplons.
Results
Microscopic model
Figure 1a illustrates the lattice geometry and the interactions between the spins in SrCu2(BO3)2. The Hamiltonian is given by
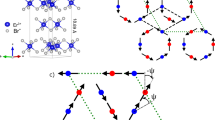
(a) Heisenberg and DM couplings in SrCu2(BO3)2. The red and blue arrows on dimers represent the intra-dimer DM vectors D (black arrows indicate the order of spins in the DM term). The inter-dimer coupling D′ has in-plane and out-of-plane components. Following the circular arrows as indicated, the out-of-plane DM component points out of the plane (purple circles). The ‘staggered’ in-plane component is shown by magenta arrows. The green rectangle indicates the structural unit cell. (b) The new reduced unit cell upon taking the two dimers to be equivalent is shown in the yellow square. The dimers form a square lattice as shown.

J is the strength of the exchange coupling on intra-dimer bonds. The intra-dimer DM coupling D is allowed by symmetry below a structural phase transition at T∼395 K (refs 32, 33; see Supplementary Figs 1 and 2, Supplementary Table 1 and Supplementary Note 1). We have included a small magnetic field hz perpendicular to the SrCu2(BO3)2 plane, with the g-factor denoted as gz. On the inter-dimer bonds, J′ and D′ are the exchange and DM couplings, respectively, with the dominant DM component being out-of-plane. As seen in Fig. 1a, the out-of-plane  couplings encode a sense of clockwise rotation; this ultimately drives a Hall effect of triplon excitations as we report below.
couplings encode a sense of clockwise rotation; this ultimately drives a Hall effect of triplon excitations as we report below.
Triplon description
A thorough bond operator treatment of the Hamiltonian in equation 1 has been presented in ref. 30. We present a simplified treatment suitable for SrCu2(BO3)2 in a weak magnetic field. Previous studies have largely focused on plateau phases at high fields(ref. 34 and references therein). In contrast, we show that the low-field regime has exotic topological properties.
In a given dimer, the Hilbert space is spanned by a singlet  and three triplets:
and three triplets:  and
and  . In the pure Shastry–Sutherland model, the ground state is a direct product of singlets |s〉 over the dimers as long as J′≲0.675 J (refs 18, 35, 36). In SrCu2(BO3)2, as the DM anisotropies are small compared with J, we assume that the ground state remains a product wavefunction. Minimizing the overall energy, we find that the ground state has the wavefunction
. In the pure Shastry–Sutherland model, the ground state is a direct product of singlets |s〉 over the dimers as long as J′≲0.675 J (refs 18, 35, 36). In SrCu2(BO3)2, as the DM anisotropies are small compared with J, we assume that the ground state remains a product wavefunction. Minimizing the overall energy, we find that the ground state has the wavefunction  and
and  on horizontal and vertical dimers, respectively; the direction of D on each dimer determines whether |ty〉 or |tx〉 is admixed. The triplet admixture is proportional to the intra-dimer DM coupling |D| with
on horizontal and vertical dimers, respectively; the direction of D on each dimer determines whether |ty〉 or |tx〉 is admixed. The triplet admixture is proportional to the intra-dimer DM coupling |D| with  . Here, as in the rest of this article, we only retain terms up to linear order in D,D′, and hz, which are small compared with the J′s.
. Here, as in the rest of this article, we only retain terms up to linear order in D,D′, and hz, which are small compared with the J′s.
On each dimer, we choose a new Hilbert space by rotating  to
to  using
using

on horizontal and vertical dimers, respectively. In the ground state, each dimer is in the  state given by the first row in the corresponding W matrix. We have three local excitations given by the mutually orthogonal triplon states
state given by the first row in the corresponding W matrix. We have three local excitations given by the mutually orthogonal triplon states  ,
,  and
and  .
.
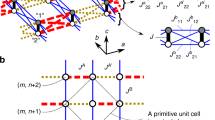
At low-magnetic fields, the low-energy excitations are spanned by single-triplon states with their dynamics captured by hopping processes of the form  . Introducing a bosonic representation for triplons, we obtain a Hamiltonian with purely hopping-like terms. By defining Wv as above with complex entries, the Hamiltonian takes on a convenient form, viz., the two dimers in the unit cell become equivalent (see Supplementary Note 2 for details). We may henceforth drop v/h indices and work with the reduced unit cell in Fig. 1b. In momentum space, the Brillouin zone (BZ) is enlarged as shown in Fig. 2b.
. Introducing a bosonic representation for triplons, we obtain a Hamiltonian with purely hopping-like terms. By defining Wv as above with complex entries, the Hamiltonian takes on a convenient form, viz., the two dimers in the unit cell become equivalent (see Supplementary Note 2 for details). We may henceforth drop v/h indices and work with the reduced unit cell in Fig. 1b. In momentum space, the Brillouin zone (BZ) is enlarged as shown in Fig. 2b.
(a) A spin-1 Dirac cone with three bands touching. (b) Triplon dispersion for hz=0. The basal plane shows the enlarged BZ corresponding to one dimer per unit cell, with k=(π,π) at the M and k=(π,0) and (π,0) at the X points. The smaller structural BZ is shown in green. The band structure hosts spin-1 Dirac cones at the BZ edge centres X. (c–e) Evolution of triplon bands and Chern numbers upon tuning magnetic field. Bands with non-zero Chern number appear for 0<hz<hc and are shown in colour. At hz=hc (d), the bands touch at a spin-1 Dirac cone at Γ. For hz>hc as in e, the Chern numbers remain zero.
For a more complete treatment, we may include pairing-like terms ( ) within a bond operator formalism as in ref. 30. We ignore such terms as they do not change the triplon energies to linear order in D, D′ and hz; we have checked that their inclusion does not alter the results presented here.
) within a bond operator formalism as in ref. 30. We ignore such terms as they do not change the triplon energies to linear order in D, D′ and hz; we have checked that their inclusion does not alter the results presented here.
Spin-1 Dirac cone physics
The triplon Hamiltonian in momentum space is given by

where the Hamiltonian matrix is given by

with γ1(k)=sin kx, γ2(k)=sin ky and  (see Supplementary Note 2 for details). Only two components of the inter-dimer DM coupling enter the Hamiltonian, viz., the out-of-plane component
(see Supplementary Note 2 for details). Only two components of the inter-dimer DM coupling enter the Hamiltonian, viz., the out-of-plane component  and the ‘staggered’ component shown in Fig. 1a. A third non-staggered component is allowed by symmetry, but does not appear at this level (see Supplementary Fig. 2 and Supplementary Note 1). Intra-dimer D and in-plane inter-dimer
and the ‘staggered’ component shown in Fig. 1a. A third non-staggered component is allowed by symmetry, but does not appear at this level (see Supplementary Fig. 2 and Supplementary Note 1). Intra-dimer D and in-plane inter-dimer  act in consonance so that only the linear combination
act in consonance so that only the linear combination  appears in the Hamiltonian similar to the analysis in ref. 29. In the following, we use the values J=722 GHz,
appears in the Hamiltonian similar to the analysis in ref. 29. In the following, we use the values J=722 GHz,  ,
,  and gz=2.28 in the M(k) matrix, which reproduce the ESR data in ref. 24. The parameter J is not the microscopic exchange strength, but rather the measured spin gap, which determines the effective coupling in the presence of quantum fluctuations.
and gz=2.28 in the M(k) matrix, which reproduce the ESR data in ref. 24. The parameter J is not the microscopic exchange strength, but rather the measured spin gap, which determines the effective coupling in the presence of quantum fluctuations.
The M(k) matrix is of the form

where 1 is the 3 × 3 identity matrix and

is a vector of 3 × 3 matrices satisfying the [Lξ, Lη]=iɛξηζ Lζ SU(2) algebra. Thus, in momentum space, the triplons behave as (pseudo)spin-1 objects coupled to a pseudomagnetic field

We now draw an analogy with the usual two-band physics wherein the 2 × 2 Hamiltonian takes the same form as equation (5) but with spin-1/2 Pauli matrices instead of spin-1 L matrices. There, we obtain two bands corresponding to eigenvalues J±d(k)/2 (we denote d(k)=|d(k)|). If d(k) is non-zero throughout the BZ, we obtain two well-separated bands whose Chern numbers are ±Ns, where Ns is the number of skyrmions in the d(k) field over the BZ37. The d(k) field contains all information about the band structure; its skyrmion count determines the topological character of bands. We emphasize here that topological properties will not change with small corrections to the Hamiltonian such as next-nearest neighbour hopping (see Supplementary Figs 3 and 4, and Supplementary Note 3).
Likewise, in our spin-1 realization, we read off the eigenvalues as {J+d(k),J,J−d(k)}. Note that the band in the middle is always flat with energy J, irrespective of the value of d(k). If the pseudomagnetic field d(k) vanishes at some k, all three bands touch in a ‘spin-1 Dirac cone’, resembling graphene but with an additional flat band passing through the band touching point. If d(k) is non-zero throughout the BZ, the spectrum consists of three well-separated triplon bands with well-defined Chern numbers {−2Ns,0,+2Ns}, where Ns is again the skyrmion number. More generally, for the arbitrary spin-S generalization of equation (5), we have (2S+1) bands with Chern numbers {−2SNs,−2(S−1)Ns,…, 2(S−1), 2SNs} (see Supplementary Table 2 and Supplementary Note 4).
Magnetic field-tuned topological transitions
The magnetic field hz provides a handle to tune topological transitions in SrCu2(BO3)2, as shown in Fig. 2. With small magnetic fields, even though the ground state remains a product of dimer singlets, the band structure of excitations shows topological transitions. When hz=0, the three bands touch at the edge centres of the BZ (corresponding to corners in the structural BZ). A small applied field opens a non-trivial band gap, allowing for three well-separated bands with Chern numbers {−2,0,+2} or {+2,0,−2}, depending on the sign of hz. When the field reaches a threshold strength  , the three bands touch at the Γ point. Indeed, this band touching has already been seen in ESR24 and infrared absorption25 spectra at hz≈1.4 T; however, its significance as a spin-1 Dirac point was not appreciated. As hz is increased further, a trivial band gap opens with all three Chern numbers being zero.
, the three bands touch at the Γ point. Indeed, this band touching has already been seen in ESR24 and infrared absorption25 spectra at hz≈1.4 T; however, its significance as a spin-1 Dirac point was not appreciated. As hz is increased further, a trivial band gap opens with all three Chern numbers being zero.
The topology of triplon bands can be understood in terms of the d(k) field. To every point in the two-dimensional (2D) BZ (an  torus), we assign the 3D vector d(k): this gives us a closed 2D surface embedded in three dimensions. If the bands are to remain well-separated, the surface cannot touch the origin, that is, d(k)≠0 anywhere in the BZ. The origin is thus special and acts as a monopole for Berry phase. The topology of the band structure reduces to whether or not the 2D surface encloses the origin; if it does, how many times does it wrap around the origin? This defines a skyrmion number
torus), we assign the 3D vector d(k): this gives us a closed 2D surface embedded in three dimensions. If the bands are to remain well-separated, the surface cannot touch the origin, that is, d(k)≠0 anywhere in the BZ. The origin is thus special and acts as a monopole for Berry phase. The topology of the band structure reduces to whether or not the 2D surface encloses the origin; if it does, how many times does it wrap around the origin? This defines a skyrmion number  , that is related to the Chern number.
, that is related to the Chern number.
To see the role of hz, we note that it enters solely as an additive contribution in the z-component of d(k). As shown in Fig. 3, the BZ maps to a closed surface of width  and height proportional to
and height proportional to  , which is composed of an upper and a lower chamber. The chambers are disconnected, but touch along line nodes. The surface is orientable: the outer surface of the lower chamber smoothly connects to the inner surface of the upper chamber and vice versa. When |hz|>hc, neither chamber encloses the origin; we have Ns=0 with all Chern numbers zero (Fig. 3a,d). When −hc<hz<0, the origin lies inside the upper chamber (Fig. 3b), the net Berry flux is positive and Chern numbers are {+2,0,−2}. When 0<hz<hc, the origin lies inside the lower chamber (Fig. 3c), the Berry flux is negative and Chern numbers are {−2,0,+2}.
, which is composed of an upper and a lower chamber. The chambers are disconnected, but touch along line nodes. The surface is orientable: the outer surface of the lower chamber smoothly connects to the inner surface of the upper chamber and vice versa. When |hz|>hc, neither chamber encloses the origin; we have Ns=0 with all Chern numbers zero (Fig. 3a,d). When −hc<hz<0, the origin lies inside the upper chamber (Fig. 3b), the net Berry flux is positive and Chern numbers are {+2,0,−2}. When 0<hz<hc, the origin lies inside the lower chamber (Fig. 3c), the Berry flux is negative and Chern numbers are {−2,0,+2}.
The key ingredient that gives rise to topological properties is the DM interaction that originates from relativistic spin-orbit coupling. The threshold magnetic field hc is proportional to the coupling  . The intra-dimer DM coupling D also plays a role: we do not find any Chern bands upon setting D=0, as is appropriate for T>395 K, above a structural transition in SrCu2(BO3)2.
. The intra-dimer DM coupling D also plays a role: we do not find any Chern bands upon setting D=0, as is appropriate for T>395 K, above a structural transition in SrCu2(BO3)2.
Edge states
The topological character of bands is revealed when edges are introduced. For 0<hz<hc (and for −hc<hz<0), edge states connecting the Chern bands appear within the bulk band gap, as shown in Fig. 4a for a strip geometry. Apart from recovering the bulk bands, we clearly see four edge states consistent with bulk boundary correspondence38 for Chern numbers ±2. The edge states constitute two ‘right-movers’ and two ‘left-movers’ (with group velocity pointing right/left), localized on the opposite edges of the strip. The wave functions of the edge states decay exponentially into the bulk, as shown in Fig. 4b.
(a) Band structure of SrCu2(BO3)2 on a cylindrical strip periodic in x, but with open edges along y. The width along y is taken to be very large. We recover the bulk states corresponding to three triplon bands. In addition, four edge states appear, connecting the Chern bands. Edge modes shown in blue and cyan (red and brown) are left-movers (right-movers). (b) Wavefunctions of the four edge states for an arbitrary kx on a strip of width W=8 dimers. The colour of the dimer bond represents the triplon weight with black corresponding to zero. Right-moving edge states are localized on the bottom edge, whereas left-movers are localized on the top edge.
Thermal Hall effect
Chern bands in electronic systems can be easily probed by doping the system so that the Fermi level lies in the band gap. This gives a transverse electrical conductivity quantized to integer values. In bosonic systems where this is not possible, the thermal Hall effect provides an alternative. Semi-classical analysis shows that a wave packet in a Chern band undergoes rotational motion39,40. To exploit this, a temperature gradient is used to populate the band differently at the system’s edges. The rotational motion of the triplons is then unbalanced, leading to a transverse triplon current. As triplons carry energy, this leads to a measurable transverse thermal current.
An expression for thermal Hall conductivity was derived using the Kubo formula in ref. 5. Subsequently, Matsumoto et al.7 showed that there is an extra contribution from the orbital motion of excitations. Figure 5a shows the thermal Hall conductivity as a function of external magnetic field calculated using the expression in ref. 7. SrCu2(BO3)2 is quasi-2D and the Hall response in each layer is in the same direction. Therefore, we add the contribution from each layer to get κxy for a three-dimensional sample (see Supplementary Note 5). As the magnetic field is tuned away from hz=0, a non-zero Hall signal develops with the sign of κxy depending on the direction of magnetic field. When the threshold magnetic field strength hc is reached, the topological nature of triplon bands is lost and the Hall signal is diminished. Figure 5b shows the peak thermal Hall conductivity increasing monotonically with background temperature. Our calculation assumes that the temperature is low enough that the triplon bands are weakly populated, allowing us to neglect triplon–triplon interactions. We expect this assumption to hold atleast until ∼5 K where the filling of bosons is ∼0.2%. Neutron scattering data show that the intensity of the single triplet excitations is essentially unchanged up to 5 K showing no damping26.
(a) Thermal Hall conductivity versus external magnetic field at different temperatures. The threshold fields hz=±hc are shown as vertical dashed lines. (b) Thermal Hall signal at hz=hc/2 versus temperature. The circles are direct evaluation of the formula, the line is an approximation applicable to SrCu2(BO3)2 in the limit where bandwidths are much smaller than the gap. (c) The filling fraction (boson occupation number) for the three bands, indexed by Chern numbers. It grows much slower with temperature than κxy.
Discussion
We have demonstrated that SrCu2(BO3)2 hosts a Hall effect of triplons. A small external magnetic field of the order of a few Tesla suffices to tune topological transitions in the band structure. The triplons form novel spin-1 Dirac cones with threefold band touching. Such a feature has been seen in various contexts41,42,43,44,45. Our study elucidates its implications for band structure topology; the spin-1 structure naturally gives Chern numbers ±2 instead of the more common ±1. Similar topological phases could exist in dimer compounds such as Rb2Cu3SnF12 (refs 46, 47) with non-zero DM couplings, and possibly in ZnCu3(OH)6Cl2 (Herbertsmithite)48.
We predict a thermal Hall signature in SrCu2(BO3)2 that can be verified by transport measurements. We also suggest neutron scattering experiments to study the evolution of band structure in low-magnetic fields (≲2 T). Such measurements can see the spin-1 Dirac cone features at hz=0 and hz=hc. It may even be possible to directly probe the edge states using precise low-angle scattering measurements.
Additional information
How to cite this article: Romhányi, J. et al. Hall effect of triplons in a dimerized quantum magnet. Nat. Commun. 6:6805 doi: 10.1038/ncomms7805 (2015).
References
Raghu, S. & Haldane, F. D. M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 78, 033834 (2008) .
Petrescu, A., Houck, A. A. & Le Hur, K. Anomalous Hall effects of light and chiral edge modes on the Kagomé lattice. Phys. Rev. A 86, 053804 (2012) .
Rechtsman, M. C. et al. Photonic floquet topological insulators. Nature 496, 196–200 (2013) .
Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J. M. Imaging topological edge states in silicon photonics. Nat. Photonics 7, 1001–1005 (2013) .
Katsura, H., Nagaosa, N. & Lee, P. A. Theory of the thermal Hall effect in quantum magnets. Phys. Rev. Lett. 104, 066403 (2010) .
Shindou, R., Matsumoto, R., Murakami, S. & Ohe, J-I. Topological chiral magnonic edge mode in a magnonic crystal. Phys. Rev. B 87, 174427 (2013) .
Matsumoto, R. & Murakami, S. Theoretical prediction of a rotating magnon wave packet in ferromagnets. Phys. Rev. Lett. 106, 197202 (2011) .
Ideue, T. et al. Effect of lattice geometry on magnon Hall effect in ferromagnetic insulators. Phys. Rev. B 85, 134411 (2012) .
Zhang, L., Ren, J., Wang, J.-S. & Li, B. Topological magnon insulator in insulating ferromagnet. Phys. Rev. B 87, 144101 (2013) .
Zhang, L., Ren, J., Wang, J.-S. & Li, B. Topological nature of the phonon Hall effect. Phys. Rev. Lett. 105, 225901 (2010) .
Zhang, L., Ren, J., Wang, J.-S. & Li, B. The phonon Hall effect: theory and application. J. Phys. Condens. Matter 23, 305402 (2011) .
Qin, T., Zhou, J. & Shi, J. Berry curvature and the phonon Hall effect. Phys. Rev. B 86, 104305 (2012) .
van Hoogdalem, K. A., Tserkovnyak, Y. & Loss, D. Magnetic texture-induced thermal Hall effects. Phys. Rev. B 87, 024402 (2013) .
Onose, Y. et al. Observation of the magnon Hall effect. Science 329, 297–299 (2010) .
Smith, R. W. & Keszler, D. A. Syntheses and crystal structures of the α- and Î2-forms of the orthoborate SrCu2(BO3)2 . J. Solid State Chem. 81, 305–313 (1989) .
Kageyama, H. et al. Exact dimer ground state and quantized magnetization plateaus in the two-dimensional spin system SrCu2(BO3)2 . Phys. Rev. Lett. 82, 3168–3171 (1999) .
Shastry, B. S. & Sutherland, B. Exact ground state of a quantum mechanical antiferromagnet. Physica B+C 108, 1069–1070 (1981) .
Miyahara, S. & Ueda, K. Exact dimer ground state of the two dimensional Heisenberg spin system SrCu2(BO3)2 . Phys. Rev. Lett. 82, 3701–3704 (1999) .
Sachdev, S. & Bhatt, R. N. Bond-operator representation of quantum spins: mean-field theory of frustrated quantum Heisenberg antiferromagnets. Phys. Rev. B 41, 9323–9329 (1990) .
Giamarchi, T., Ruegg, C. & Tchernyshyov, O. Bose-Einstein condensation in magnetic insulators. Nat. Phys. 4, 198–204 (2008) .
Schmidt, K. P. & Uhrig, G. S. Excitations in one-dimensional quantum antiferromagnets. Phys. Rev. Lett. 90, 227204 (2003) .
Knetter, C. & Uhrig, G. S. Dynamic structure factor of the two-dimensional Shastry-Sutherland model. Phys. Rev. Lett. 92, 027204 (2004) .
Momoi, T. & Totsuka, K. Magnetization plateaus of the Shastry-Sutherland model for SrCu2(BO3)2: spin-density wave, supersolid, and bound states. Phys. Rev. B 62, 15067–15078 (2000) .
Nojiri, H., Kageyama, H., Ueda, Y. & Motokawa, M. ESR study on the excited state energy spectrum of SrCu2(BO3)2 –a central role of multiple-triplet bound states–. J. Phys. Soc. Jpn 72, 3243–3253 (2003) .
Rõõm, T. et al. Far-infrared spectroscopy of spin excitations and Dzyaloshinskii-Moriya interactions in the Shastry-Sutherland compound SrCu2(BO3)2 . Phys. Rev. B 70, 144417 (2004) .
Gaulin, B. D. et al. High-resolution study of spin excitations in the singlet ground state of SrCu2(BO3)2 . Phys. Rev. Lett. 93, 267202 (2004) .
Gozar, A., Dennis, B. S., Kageyama, H. & Blumberg, G. Symmetry and light coupling to phononic and collective magnetic excitations in SrCu2(BO3)2 . Phys. Rev. B 72, 064405 (2005) .
Cépas, O. et al. Dzyaloshinskii-Moriya interaction in the 2D spin gap system SrCu2(BO3)2 . Phys. Rev. Lett. 87, 167205 (2001) .
Cheng, Y. F., Cépas, O., Leung, P. W. & Ziman, T. Magnon dispersion and anisotropies in SrCu2(BO3)2 . Phys. Rev. B 75, 144422 (2007) .
Romhányi, J., Totsuka, K. & Penc, K. Effect of Dzyaloshinskii-Moriya interactions on the phase diagram and magnetic excitations of SrCu2(BO3)2 . Phys. Rev. B 83, 024413 (2011) .
Miyahara, S. et al. The effects of intra-dimer Dzyaloshinsky–Moriya interaction on the properties of SrCu2(BO3)2 in an external magnetic field. J. Phys. Condens. Matter 16, S911–S916 (2004) .
Smith, R. W. & Keszler, D. A. Synthesis, structure, and properties of the orthoborate SrCu2(BO3)2 . J. Solid State Chem. 93, 430–435 (1991) .
Sparta, K. et al. Structural phase transition in the 2D spin dimer compound SrCu2(BO3)2 . Eur. Phys. J. B 19, 507–516 (2001) .
Matsuda, Y. H. et al. Magnetization of SrCu2(BO3)2 in ultrahigh magnetic fields up to 118T. Phys. Rev. Lett. 111, 137204 (2013) .
Koga, A. & Kawakami, N. Quantum phase transitions in the Shastry-Sutherland model for SrCu2(BO3)2 . Phys. Rev. Lett. 84, 4461–4464 (2000) .
Corboz, P. & Mila, F. Tensor network study of the Shastry-Sutherland model in zero magnetic field. Phys. Rev. B 87, 115144 (2013) .
Bernevig, B. A. & Hughes, T.L. in Topological Insulators and Topological Superconductors Ch. 8, Princeton Univ. (2013) .
Hatsugai, Y. Chern number and edge states in the integer quantum Hall effect. Phys. Rev. Lett. 71, 3697–3700 (1993) .
Sundaram, G. & Niu, Q. Wave-packet dynamics in slowly perturbed crystals: gradient corrections and berry-phase effects. Phys. Rev. B 59, 14915–14925 (1999) .
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010) .
Apaja, V., Hyrkäs, M. & Manninen, M. Flat bands, Dirac cones, and atom dynamics in an optical lattice. Phys. Rev. A 82, 041402 (2010) .
Huang, X., Lai, Y., Zheng, H. & Chan, C. T. Dirac cones induced by accidental degeneracy in photonic crystals and zero-refractive-index materials. Nat. Mater. 10, 582–586 (2011) .
Asano, K. & Hotta, C. Designing Dirac points in two-dimensional lattices. Phys. Rev. B 83, 245125 (2011) .
Dóra, B., Kailasvuori, J. & Moessner, R. Lattice generalization of the Dirac equation to general spin and the role of the flat band. Phys. Rev. B 84, 195422 (2011) .
Yamashita, Y., Tomura, M., Yanagi, Y. & Ueda, K. SU(3) Dirac electrons in the 1/5-depleted square-lattice Hubbard model at 1/4 filling. Phys. Rev. B 88, 195104 (2013) .
Matan, K. et al. Pinwheel valence-bond solid and triplet excitations in the two-dimensional deformed Kagomé lattice. Nat. Phys. 6, 865–869 (2010) .
Hwang, K., Park, K. & Kim, Y. B. Influence of Dzyaloshinskii-Moriya interactions on magnetic structure of a spin-1/2 deformed Kagomé lattice antiferromagnet. Phys. Rev. B 86, 214407 (2012) .
Tovar, M., Raman, K. S. & Shtengel, K. Dzyaloshinskii-moriya interactions in valence-bond systems. Phys. Rev. B 79, 024405 (2009) .
Acknowledgements
We thank R. Shankar (Chennai), A. Paramekanti and M. Daghofer for useful discussions. This work was supported by the Hungarian OTKA Grant No. 106047.
Author information
Authors and Affiliations
Contributions
All authors contributed to all aspects of this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-4, Supplementary Tables 1-2, Supplementary Notes 1-5 and Supplementary References (PDF 770 kb)
Rights and permissions
About this article
Cite this article
Romhányi, J., Penc, K. & Ganesh, R. Hall effect of triplons in a dimerized quantum magnet. Nat Commun 6, 6805 (2015). https://doi.org/10.1038/ncomms7805
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms7805
This article is cited by
-
Discovery of quantum phases in the Shastry-Sutherland compound SrCu2(BO3)2 under extreme conditions of field and pressure
Nature Communications (2022)
-
Thermally populated versus field-induced triplon bound states in the Shastry-Sutherland lattice SrCu2(BO3)2
npj Quantum Materials (2021)
-
Quantum Tunneling in the \(\alpha -T_3\) Model with an Effective Mass Term
Journal of Low Temperature Physics (2020)
-
Triplon band splitting and topologically protected edge states in the dimerized antiferromagnet
Nature Communications (2019)
-
Photoinduced Topological Phase Transitions in Topological Magnon Insulators
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.