Abstract
Recently discovered relativistic spin torques induced by a lateral current at a ferromagnet/paramagnet interface are a candidate spintronic technology for a new generation of electrically controlled magnetic memory devices. The focus of our work is to experimentally disentangle the perceived two model physical mechanisms of the relativistic spin torques, one driven by the spin-Hall effect and the other one by the inverse spin-galvanic effect. Here, we show a vector analysis of the torques in a prepared epitaxial transition-metal ferromagnet/semiconductor-paramagnet single-crystal structure by means of the all-electrical ferromagnetic resonance technique. By choice of our structure in which the semiconductor paramagnet has a Dresselhaus crystal inversion asymmetry, the system is favourable for separating the torques due to the inverse spin-galvanic effect and spin-Hall effect mechanisms into the field-like and antidamping-like components, respectively. Since they contribute to distinct symmetry torque components, the two microscopic mechanisms do not compete but complement each other in our system.
Similar content being viewed by others
Introduction
The two considered microscopic origins of the relativistic spin torques observed at a ferromagnet/paramagnet interface1,2 have the following basic characteristics: in one picture, a spin current generated in the paramagnet via the relativistic spin-Hall effect3 (SHE) is absorbed in the ferromagnet and induces the spin transfer torque4 (STT). In the other picture, a non-equilibrium spin-density is generated via the relativistic inverse spin-galvanic effect5 (ISGE) and induces the spin–orbit torque6,7,8 (SOT) in the ferromagnet. From the early observations in paramagnetic semiconductors, SHE and ISGE are known as companion phenomena that can both allow for electrically aligning spins in the same structure9,10,11. It is therefore both challenging and desirable for our basic physical understanding of the spin torques at the ferromagnet/paramagnet interface to experimentally disentangle the SHE and ISGE contributions.
The splitting of the two microscopic mechanisms between the field-like and the antidamping-like torque components has not been previously achieved for several conceptual reasons. The original theoretical proposals12,13,14 and experimental observations10,11,15,16 of the ISGE were made in paramagnets with no ferromagnetic component in the structure. The corresponding non-equilibrium spin density, generated in the ISGE by inversion-asymmetry terms in the relativistic Hamiltonian, has naturally no dependence on magnetization. Hence, in the context of magnetic semiconductors6,8,17,18 or ferromagnet/paramagnet structures1,7,19,20,21, the ISGE may be expected to yield only the field-like component of the torque ~M × ζ, where the vector ζ is independent of the magnetization vector M (see Fig. 1a). However, when carriers experience both the spin–orbit coupling and magnetic exchange coupling, the inversion asymmetry can generate a non-equilibrium spin density component of extrinsic, scattering-related22,23 or intrinsic Berry-curvature24,25,26 origin, which is magnetization dependent and yields an antidamping-like torque ~M × (M × ζ). Experiments in (Ga,Mn)As confirmed the presence of the ISGE-based mechanism8,17,18 and demonstrated that the field-like and the Berry-curvature antidamping-like SOT components can have comparable magnitudes25.
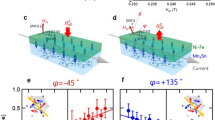
(a) In the paramagnetic GaAs layer (PM), as charge carriers are accelerated by an applied electric field in the inversion-asymmetric crystal potential, scattering events lead to a non-equilibrium spin polarization. The spin polarization depends on the direction of the current with respect to crystal direction. Through exchange coupling at the interface, the magnetization, M, in the ferromagnetic layer (FM) experiences an effective field, hISGE, parallel to the spin polarization. (b) In the GaAs layer, when a longitudinal charge current, Jc, is applied, a transverse spin current, Js, is induced by the SHE, which flows into the Fe layer. The spin current exerts a torque that depends on the magnetization angle. For an in-plane magnetization this is described by an out-of-plane effective field, hSHE. (c) In transition-metal bilayers, only a Rashba-symmetry spin polarization may be generated by the structural inversion asymmetry. (d) In GaAs, the spin polarization of the ISGE has the Dresselhaus symmetry for carrier momentum in different crystal directions.
The STT is dominated by the antidamping-like component4 in weakly spin–orbit-coupled ferromagnets with τex≪τs, where τex is the precession time of the carrier spins in the exchange field of the ferromagnet and τs is the spin lifetime in the ferromagnet. This, in principle, applies also to the case when the spin current is injected to the ferromagnet from a paramagnet via the SHE (see Fig. 1b). However, at finite τs, the STT also acquires a field-like component4. Experiments in W/Hf/CoFeB structures confirmed the presence of the SHE-based mechanism in the observed torques and showed that the SHE–STT can have both antidamping-like and field-like components of comparable magnitudes27.
In the commonly studied polycrystalline transition-metal ferromagnet/heavy-metal paramagnet samples, the dependence of the torques on the angle of the driving in-plane current also does not provide the direct means to disentangle the two microscopic origins. The lowest-order inversion-asymmetry spin–orbit terms in the Hamiltonian have the Rashba form (see Fig. 1c) for which the vector ζ is in the plane parallel to the interface and perpendicular to the current, independent of the current direction. The same applies to the spin polarization of the SHE spin current propagating from the paramagnet to the ferromagnet. The M and ζ functional form of the field-like and antidamping-like SHE–STTs is the same as of the corresponding SOT components. In the observed lowest-order torque terms in Pt/Co and Ta/CoFeB structures28, the ISGE-based and the SHE-based mechanism remained, therefore, indistinguishable. The simultaneous observation of higher-order torque terms in these samples pointed to SOTs due to structural inversion-asymmetry terms beyond the basic Rashba model. From the Ta thickness dependence measurements in the Ta/CoFeB structure, it was concluded that in these samples both the ISGE-based and the SHE-based mechanisms contributed to both the field-like and the antidamping-like torques29.
The SHE and ISGE were originally discovered in III–V semiconductors9,10,11,15,16 but for maximizing the relativistic spin torques in common transition-metal ferromagnets, it turned out to be more suitable to interface them with the highly conductive heavy-metal paramagnets such as Pt, Ta or W1,2,27,28,29. To clearly separate the two microscopic origins of the torques, returning to III–V semiconductor paramagnets is instrumental as the leading inversion-asymmetric term is played by the broken inversion symmetry in the crystal structure. Independent of the interface, holes in the strained zinc-blende lattice of a III–V semiconductor experience a linear-in-wavevector Dresselhaus spin–orbit coupling. The ISGE of the corresponding symmetry (see Fig. 1d) generated in the semiconductor should induce a SOT in an adjacent ferromagnetic film with ζ perpendicular to the current for current along [110] or  crystal axes of the semiconductor, while ζ should be parallel to the current for the [100] or [010] current directions.
crystal axes of the semiconductor, while ζ should be parallel to the current for the [100] or [010] current directions.
In the following, we measure the relativistic spin torques in a single crystal Fe (2 nm)/(Ga,Mn)As (20 nm) bilayer using an electrically induced and detected ferromagnetic resonance (FMR) technique18,30 (for growth details see Methods). We dope the GaAs host with ~3% of substitutional MnGa acceptors to increase the semiconductor conductivity, while not providing a sizeable exchange splitting within the semiconductor at room temperature. From magnetization angle dependence measurements of the FMR voltages, we find the field-like and antidamping torques have similar magnitudes. By measuring devices where the current is along different crystal directions of the semiconductor, we show that the ISGE with a characteristic Dresselhaus symmetry induces only the field-like torque in the adjacent Fe, whereas the SHE spin current, generated inside the paramagnetic p-doped GaAs layer, is absorbed in the weakly spin–orbit-coupled Fe in the form of the antidamping-like STT. Therefore in this bilayer, we show that the ISGE and SHE mechanisms are separated into distinct symmetry components of the current-induced torque.
Results
Electrically-induced FMR measurements
Current-induced torques were measured in patterned bars of width 10μm and length 200μm using an all-electrical FMR technique (see Fig. 2a). In this method, a microwave current flowing in the device induces FMR when the externally applied magnetic field matches the resonant condition. The resonance of the Fe magnetization is detected in the d.c. voltage induced across the bar, Vd.c.. This is due to the homodyne mixing of the microwave current with the oscillating component of magnetoresistance caused by the magnetization precession. In these measurements, we increase the microwave current coupled into the sample, with a typical resistance of 8 kΩ, using an impedance matching network30 (see Methods and Supplementary Note 1).
(a) Schematic of the measurement showing magnetization precession. A microwave current passes through the capacitor of the bias-T and into the Fe/GaAs bilayer sample where the current-induced torques causes the magnetization of the Fe (purple arrow) to precess around the external field (black arrow). The precession is detected in the d.c. voltage measured across the device by a magnetoresistance mixing effect. (b) A typical FMR curve is detected in Vd.c. (data points) as a function of external field, induced by a 16.245GHz microwave current. Vd.c. is fitted (solid green line) by a combination of symmetric (red dotted line) and antisymmetric (blue dashed line) Lorentzians. (c) The in-plane magnetization angle dependence of the fitted Lorentzian amplitudes for a device with current in the [010] crystal direction.
For a series of external magnetic field directions in the plane of the sample, FMR sweeps were recorded using a microwave frequency of close to 16 GHz. From the magnetization angle dependence of the resonance field, we obtained the magnetization amplitude value of μ0Ms=1.85±0.03 T, which is close to the literature value of 1.7 T for Fe31, and we found an in-plane uniaxial anisotropy of μ0HU=0.101±0.001 T, which is typical for thin films of Fe grown on GaAs32. By solving the Landau–Lifshitz–Gilbert equation for a small current-induced excitation field, (hx, hy, hz)ejωt, Vd.c. is found to be comprised of symmetric and antisymmetric Lorentzian functions with coefficients Vsym and Vasy, respectively. Here hx is the excitation field component parallel to the current and hy is the component perpendicular to the current. hz is the component perpendicular to the plane of the bilayer. The coefficients depend on the angle, θ, of the magnetization vector relative to the current and are given by

Here, Vmix is the sensitivity of the mixing detection and is given by  , where I0 (ejωt, 0, 0) is the microwave current in the device and ΔR is the coefficient of the anisotropic magnetoresistance of the sample. Ayy and Ayz are the diagonal and off-diagonal components of the a.c. magnetic susceptibility, which depend on the magnetic anisotropies and Gilbert damping of the sample. In our devices, ΔR is typically 17 Ω which, assuming Fe carries the majority of the current in the bilayer, is consistent in sign and magnitude with literature values of 0.2% anisotropic magnetoresistance in Fe33. We estimate the proportion of total bilayer current in the Fe layer to be 79% by resistance measurements of Hall bars before and after removing the Fe and capping Al (see Supplementary Note 2).
, where I0 (ejωt, 0, 0) is the microwave current in the device and ΔR is the coefficient of the anisotropic magnetoresistance of the sample. Ayy and Ayz are the diagonal and off-diagonal components of the a.c. magnetic susceptibility, which depend on the magnetic anisotropies and Gilbert damping of the sample. In our devices, ΔR is typically 17 Ω which, assuming Fe carries the majority of the current in the bilayer, is consistent in sign and magnitude with literature values of 0.2% anisotropic magnetoresistance in Fe33. We estimate the proportion of total bilayer current in the Fe layer to be 79% by resistance measurements of Hall bars before and after removing the Fe and capping Al (see Supplementary Note 2).
FMR measurements were made using devices patterned in four crystal directions. The microwave power for all devices, incident on the impedance matching network, was 24 dBm. For each angle, the resonances were fitted by symmetric and antisymmetric Lorentzian functions. A typical curve is shown in Fig. 2b. The in-plane uniaxial magnetic anisotropy of Fe implies that, in general, the magnetization does not lie along the external field. The actual magnetization angles and uniaxial anisotropy are self-consistently calculated from the dependence of the resonant field on the external magnetic field angle34. This also allows the susceptibilities, Ayz and Ayy, to be calculated. The magnetization angle dependence of Vsym/Ayz and Vasy/Ayy is plotted in Fig. 2c for a bar patterned in the [010] crystal direction. The full expression for the angle dependence of the fitted data is given in Supplementary Note 3.
Validity of FMR analysis
Our analysis of the current-induced torques using equation (1) is not necessarily valid if the torques do not act in phase with the microwave current. In comparison with electrically detected FMR measurements where the microwave current is capacitively or inductively coupled into the sample35, we do not expect a phase-shift between the microwave current and induced fields as the current is conducted ohmically. Nevertheless, we might worry that some part of our microwave resonator circuit leads to a phase shift. To test this, we repeated our measurements with a [100] device over a frequency range (11.8–14.4 GHz) using a microstrip resonator with a fundamental frequency close to 13 GHz (Fig. 3a). If there were some frequency-dependent phase shift, we would expect the lineshape to oscillate between an antisymmetric and symmetric Lorentzian over this frequency range. However, the ratio of Vsym to Vasy remains constant in this frequency range to within experimental error (Fig. 3b), confirming that our analysis is correct.
(a) Normalized, fitted, resonant peaks for a series of microwave frequencies detected in Vd.c.. The lineshape is dominated by an antisymmetric Lorentzian for every frequency. (b) The ratio of Vsym to Vasy (blue circles) is constant to within the standard error (red shaded region) of a linear fit (red dashed line) for the measured frequency range. The error in the ratio is bigger away from the impedance-matched frequency (13 GHz) of the microstrip resonator used, as the detected peak in Vd.c. is smaller.
Analysis of the current-induced torques
As shown in Fig. 4a, the in-plane current-induced field depends strongly on the crystal direction of the current and can be well fitted by the Dresselhaus symmetry ISGE field, hISGE~(cos 2φ[100], −sin 2φ[100], 0), where φ[100] is the angle between the current and the [100] crystal direction. This is the expected symmetry of the current-induced non-equilibrium spin polarization of carriers in the semiconductor due to the inversion-asymmetric crystal structure of the strained zinc-blende lattice of (Ga,Mn)As. The interface exchange coupling of these polarized carriers with the adjacent Fe moments induces the field-like SOT in Fe with the Dresselhaus symmetry. We note that other torque terms with the symmetry common to the Rashba ISGE, the field-like component of the SHE–STT or the torque due to an Oersted field have only a minor contribution to the total measured field-like torque.
(a) The fitted in-plane field coefficients for a set of devices in different crystal directions. (b) The fitted out-of-plane field coefficient (representing the antidamping torque) for the same devices. Error bars shown are calculated by estimating the standard deviation in Vmix due to the variance in the calibration of the microwave current.
To highlight that carriers in the semiconductor layer are responsible for the Dresselhaus symmetry ISGE field, we compare Fig. 4a with previous measurements in which the in-plane current-induced fields were measured in a bare (Ga,Mn)As epilayer25 without the Fe film. To observe the corresponding SOT in this sample, a larger concentration of magnetic Mn moments was used, and the measurements were performed at low temperatures where the Mn moments are ferromagnetic in equilibrium. Instead of the interfacial exchange coupling to Fe, the current-induced non-equilibrium spin polarization of carriers in the semiconductor due to the Dresselhaus symmetry ISGE is exchange-coupled directly to the ferromagnetic moments on which it exerts the field-like SOT. In both the Fe/(Ga,Mn)As and the (Ga,Mn)As samples the same crystal-symmetry field-like SOT is observed, which confirms their common Dresselhaus ISGE origin.
In contrast to the in-plane field, the out-of-plane current-induced field is independent of the crystal direction of the current but depends on the magnetization angle. It is dominated by a term hSHE~M × y (y is the direction transverse to the current), which generates the antidamping-like torque. As shown in Fig. 4b, the amplitudes of the field-like and antidamping-like torques are comparable in our Fe/(Ga,Mn)As structure. The underlying microscopic mechanism of the antidamping component can only be of the SHE–STT origin. The experimental error shown in Fig. 4b is greater than any crystal-dependent variation in the spin-Hall angle.
In previous measurements in the bare (Ga,Mn)As epilayer25, the antidamping-like SOT was dominated by the counterpart microscopic mechanism to the Dresselhaus ISGE. This Dresselhaus-symmetry antidamping-like SOT is clearly missing in our measured data. It is suppressed in our Fe/(Ga,Mn)As structure by design, because carriers in the semiconductor are not sufficiently magnetized at equilibrium due to the low Mn moment density and high temperature of the experiment. In principle, one might also consider that the spin accumulation induced by the Dresselhaus ISGE could cause a diffusive spin current to flow into the ferromagnet and exert an antidamping-like STT. This would have the Dresselhaus symmetry that is, however, not seen in our antidamping-like torque data.
A Rashba-symmetry antidamping-like SOT due to the carriers in the Fe experiencing the inversion asymmetry of the interface could in principle also explain the symmetry of our data; however, we do note the lack of a corresponding strong Rashba-symmetry field-like SOT. This antidamping SOT would have the same symmetry as the antidamping SHE–STT. This possibility is, however, ruled out by our control experiment in which we perform electrically detected FMR in a similar molecular beam epitaxy-grown Fe (1 nm)/insulating GaAs structure at room temperature. In this case, we do not observe the antidamping torque in the rectification effect, despite the sample possessing a similar magnetoresistance ratio (~0.2%) to our Fe/(Ga,Mn)As. This is consistent with the carriers being removed from the semiconductor, which eliminates the SHE source of the spin current. We note that also consistently with the absence of carriers in the semiconductor in the Fe/insulating GaAs structure, we do not observe the Dresselhaus-symmetry field-like SOT in this control sample.
Determining the magnitudes of the ISGE and SHE
To calibrate the microwave current in the sample we used a bolometric technique (see Supplementary Fig. 1 and Supplementary Note 4). Using this calibration, we estimate amplitudes of |μ0hISGE/JGaAs|=16±10 μT per 106 A cm−2 and |μ0hSHE/JGaAs|=20±9 μT per 106 A cm−2. The error is found from the statistical variation of all of the devices measured. To verify the bolometric calibration, we also perform an additional check with a single device by measuring the change in Q-factor of the microstrip resonator loaded with and without a sample (see Supplementary Figs 2 and 3 and Supplementary Note 5). This calibration yields values of |μ0hISGE/JGaAs|=37 μT per 106 A cm−2 and |μ0hSHE/JGaAs|=47 μT per 106 A cm−2, close to the values of the bolometric technique.
From the measured hSHE in our Fe/(Ga,Mn)As structure we can infer the room-temperature spin-Hall angle, θSH, in the paramagnetic (Ga,Mn)As using the expression based on the antidamping-like STT2,

Here it is assumed that the thickness of the semiconductor is much larger than its spin diffusion length (5.6 nm in p-GaAs36) and dFe is the thickness of the Fe layer. Equation (2) yields values of θSH=1.7±0.9% (bolometric calibration) and 4% (Q-factor calibration), similar to spin-Hall angles previously reported for carriers with a p-orbital character in GaAs36,37. This agreement with previously measured spin-Hall angles is further evidence that the antidamping-like torque does not have a significant Rashba-symmetry SOT contribution. To check these spin-Hall values, we compare our torque efficiencies in terms of field per total current density with those of transition metal/ferromagnet bilayers. For instance, Garello et al.28 measured an antidamping-like torque of |μ0h/J|=690 μT per 106 A cm−2 in layers with 0.6 nm Co and 3 nm Pt and an equivalent spin-Hall angle of 16%. Although our spin-Hall angle is only 4–8 times smaller, the field per total current density is 85–170 times smaller because the total magnetic moment of our Fe layer is ~4 times higher than of the Co and ~80% of the total current is shunted through the Fe.
To conclude, we have experimentally disentangled the two archetype microscopic mechanisms that can drive relativistic current-induced torques in ferromagnet/paramagnet structures. In our epitaxial Fe/(Ga,Mn)As bilayer we simultaneously observed ISGE-based and SHE-based torques of comparable amplitudes. Designed magnetization-angle and current-angle symmetries of our single-crystal structure allowed us to split the two microscopic origins between the field-like and the antidamping-like torque components. Experimentally establishing the microscopic physics of the relativistic spin torques should stimulate both the fundamental and applied research of these intriguing and practical spintronic phenomena.
Methods
Thin-film growth
To obtain measurable torques in a metal-ferromagnet/semiconductor-paramagnet structure requires at least partially matched conductances of the semiconductor and metal layers, which we achieved by doping a GaAs host with ~3% of substitutional MnGa acceptors. Mn allows us to achieve this exceptionally high charge-doping. The semiconductor (Ga,Mn)As layer of thickness 20 nm was deposited on a GaAs(001) substrate by molecular beam epitaxy at a temperature of 260 °C. The substrate temperature was then reduced to 0 °C, before depositing a 2-nm Fe layer, plus a 2-nm Al capping layer without breaking vacuum. In situ reflection high-energy electron diffraction and ex situ X-ray reflectivity and diffraction measurements confirmed that the layers are single crystalline with sub-nm interface roughness.
Impedance matching
To improve the sensitivity of the FMR measurement, the sample is embedded in a microstrip resonator circuit30, which acts to impedance match the ~8-kΩ sample to the external 50-Ω transmission line at the fundamental frequency (in this case ~8 GHz) or harmonic frequencies of the resonator (see Supplementary Note 1). To allow measurement of Vd.c., the resonator contains an on-board bias-T. In this experiment, FMR measurements are made at the the 2nd harmonic frequency of the resonator (~16 GHz).
Additional information
How to cite this article: Skinner, T. D. et al. Complementary spin-Hall and inverse spin-galvanic effect torques in a ferromagnet/semiconductor bilayer. Nat. Commun. 6:6730 doi: 10.1038/ncomms7730 (2015).
References
Miron, I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011) .
Liu, L. et al. Spin-torque switching with the giant spin hall effect of tantalum. Science 336, 555–558 (2012) .
Jungwirth, T., Wunderlich, J. & Olejnk, K. Spin hall effect devices. Nat. Mater. 11, 382–390 (2012) .
Ralph, D. & Stiles, M. D. Spin transfer torques. J. Magn. Magn. Mater. 320, 1190–1216 (2008) .
Ivchenko, E. & Ganichev, S. in Spin Physics in Semiconductors (ed Dyakonov, M. I.) Ch. 9 Springer (2008) .
Bernevig, B. A. & Vafek, O. Piezo-magnetoelectric effects in p-doped semiconductors. Phys. Rev. B 72, 033203 (2005) .
Manchon, A. & Zhang, S. Theory of nonequilibrium intrinsic spin torque in a single nanomagnet. Phys. Rev. B 78, 212405 (2008) .
Chernyshov, A. et al. Evidence for reversible control of magnetization in a ferromagnetic material by means of spin-orbit magnetic field. Nat. Phys. 5, 656–659 (2009) .
Kato, Y. K., Myers, R. C., Gossard, A. C. & Awschalom, D. D. Observation of the spin Hall effect in semiconductors. Science 306, 1910–1913 (2004) .
Kato, Y., Myers, R. C., Gossard, A. C. & Awschalom, D. D. Current induced electron spin polarization in strained semiconductors. Phys. Rev. Lett. 93, 176601 (2004) .
Wunderlich, J., Kaestner, B., Sinova, J. & Jungwirth, T. Experimental observation of the spin Hall effect in a two dimensional spin-orbit coupled semiconductor system. Phys. Rev. Lett. 94, 047204 (2005) .
Aronov, A. G. & Lyanda-Geller, Y. B. Nuclear electric resonance and orientation of carrier spins by an electric field. JETP Lett. 50, 431 (1989) .
Edelstein, V. M. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun. 73, 233–235 (1990) .
Mal'shukov, A. G. & Chao, K. A. Optoelectric spin injection in semiconductor heterostructures without a ferromagnet. Phys. Rev. B 65, 241308 (2002) .
Silov, A. Y. et al. Current-induced spin polarization at a single heterojunction. Appl. Phys. Lett. 85, 5929–5931 (2004) .
Ganichev, S. D. et al. Can an electric current orient spins in quantum wells? Preprint at http://arxiv.org/abs/cond-mat/0403641 (2004) .
Endo, M., Matsukura, F. & Ohno, H. Current induced effective magnetic field and magnetization reversal in uniaxial anisotropy (Ga,Mn)As. Appl. Phys. Lett. 97, 222501 (2010) .
Fang, D. et al. Spin-orbit driven ferromagnetic resonance: a nanoscale magnetic characterisation technique. Nat. Nanotechnol. 6, 413–417 (2011) .
Miron, I. M. et al. Current-driven spin torque induced by the Rashba effect in a ferromagnetic metal layer. Nat. Mater. 9, 230–234 (2010) .
Pi, U. H. et al. Tilting of the spin orientation induced by Rashba effect in ferromagnetic metal layer. Appl. Phys. Lett. 97, 162507 (2010) .
Suzuki, T. et al. Current-induced effective field in perpendicularly magnetized Ta/CoFeB/MgO wire. Appl. Phys. Lett. 98, 142505 (2011) .
Pesin, D. A. & MacDonald, A. H. Quantum kinetic theory of current-induced torques in rashba ferromagnets. Phys. Rev. B 86, 014416 (2012) .
Wang, X. & Manchon, A. Diffusive spin dynamics in ferromagnetic thin films with a Rashba interaction. Phys. Rev. Lett. 108, 117201 (2012) .
Garate, I. & MacDonald, A. H. Influence of a transport current on magnetic anisotropy in gyrotropic ferromagnets. Phys. Rev. B 80, 134403 (2009) .
Kurebayashi, H. et al. An anti-damping spin-orbit torque originating from the berry curvature. Nat. Nanotechnol. 9, 211–217 (2014) .
Freimuth, F., Blügel, S. & Mokrousov, Y. Spin-orbit torques in Co/Pt(111) and Mn/W(001) magnetic bilayers from first principles. Phys. Rev. B 90, 174423 (2014) .
Pai, C. et al. Enhancement of perpendicular magnetic anisotropy and transmission of spin-hall-effect-induced spin currents by a Hf spacer layer in W/Hf/CoFeB/MgO layer structures. Appl. Phys. Lett. 104, 082407 (2014) .
Garello, K. et al. Symmetry and magnitude of spin-orbit torques in ferromagnetic heterostructures. Nat. Nanotechnol. 8, 587–593 (2013) .
Kim, J. et al. Layer thickness dependence of the current-induced effective field vector in Ta|CoFeB|MgO. Nat. Mater. 12, 240–245 (2013) .
Fang, D. et al. Electrical excitation and detection of magnetic dynamics with impedance matching. Appl. Phys. Lett. 101, 182402 (2012) .
Danan, H., Herr, A. & Meyer, A. J. P. New determinations of the saturation magnetization of nickel and iron. J. Appl. Phys. 39, 669–670 (1968) .
Brockmann, M., Zolfl, M., Miethaner, S. & Bayreuther, G. In-plane volume and interface magnetic anisotropies in epitaxial Fe films on GaAs(001). J. Magn. Magn. Mater. 198-199, 384–386 (1999) .
McGuire, T. & Potter, R. Anisotropic magnetoresistance in ferromagnetic 3d alloys. IEEE Trans. Magn. 11, 1018–1038 (1975) .
Ando, K. et al. Angular dependence of inverse spin-Hall effect induced by spin pumping investigated in a NiFe/Pt thin film. Phys. Rev. Lett. 78, 014413 (2008) .
Harder, M., Cao, Z. X., Gui, Y. S., Fan, X. L. & Hu, C. M. Analysis of the line shape of electrically detected ferromagnetic resonance. Phys. Rev. B 84, 054423 (2011) .
Chen, L., Matsukura, F. & Ohno, H. Direct-current voltages in (Ga,Mn)As structures induced by ferromagnetic resonance. Nat. Commun. 4, 2055 (2013) .
Okamoto, N. et al. Electric control of the spin hall effect by intervalley transitions. Nat. Mater. 13, 932–937 (2014) .
Acknowledgements
We acknowledge support from the EU European Research Council advanced grant no. 268066, from the Ministry of Education of the Czech Republic grant no. LM2011026, from the Grant Agency of the Czech Republic grant no. 14-37427G and the Academy of Sciences of the Czech Republic Praemium Academiae. A.J.F. acknowledges support from a Hitachi research fellowship. H.K. acknowledges financial support from the Japan Science and Technology Agency.
Author information
Authors and Affiliations
Contributions
K.O., R.P.C., B.L.G. and H.K. grew the materials. K.O. and H.K. prepared the samples. T.D.S., L.K.C. and H.K. performed the experiments and T.D.S. analysed the data. T.D.S., T.J. and A.J.F. prepared the manuscript. T.D.S. and A.J.F. planned the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-3, Supplementary Table 1, Supplementary Notes 1-5 and Supplementary References (PDF 295 kb)
Rights and permissions
About this article
Cite this article
Skinner, T., Olejník, K., Cunningham, L. et al. Complementary spin-Hall and inverse spin-galvanic effect torques in a ferromagnet/semiconductor bilayer. Nat Commun 6, 6730 (2015). https://doi.org/10.1038/ncomms7730
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms7730
This article is cited by
-
Dependence of spin-orbit torque effective fields on magnetization uniformity in Ta/Co/Pt structure
Scientific Reports (2019)
-
Control of spin–orbit torques through crystal symmetry in WTe2/ferromagnet bilayers
Nature Physics (2017)
-
Room-temperature spin–orbit torque in NiMnSb
Nature Physics (2016)
-
Robust spin-orbit torque and spin-galvanic effect at the Fe/GaAs (001) interface at room temperature
Nature Communications (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.