Abstract
Sufficiently strong interactions promote coherent quantum transitions in spite of thermalization and losses, which are the adversaries of delicate effects such as reversibility and correlations. In atomic Bose–Einstein condensates (BECs), strong atom–atom interactions can eject atoms from the BEC to the normal component, yielding quantum depletion instead of temperature depletion. A recent experiment has already been verified to overcome losses. Here I show that it also achieves coherent quantum-depletion dynamics in a BEC swept fast enough from weak to strong atom–atom interactions. The elementary coherent process first excites the normal component into a liquid state that evolves into a spherical shell state, where the atom occupation peaks at a finite momentum to shield 50% of the BEC atoms from annihilation. The identified coherent processes resemble ultrafast semiconductor excitations expanding the scope of BEC explorations to many-body non-equilibrium studies.
Similar content being viewed by others
Introduction
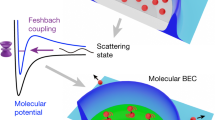
Strong interactions1,2,3 are prerequisite for efficient quantum-state manipulations hindered by dissipation and thermalization. For ultracold atoms, thermalization4 itself is advantageous because it creates the Bose–Einstein condensate (BEC) from the normal component, whereas quantum depletion5,6 ejects atoms from the BEC via interactions. However, coherent quantum depletion is reversible because it is driven by a distinct coherent transition amplitude between the BEC and normal-component atoms, unlike losses and thermal depletion4. Atom–atom interactions may also bind atoms to clusters within a range defined by the atomic scattering length7, ascatt, that can be substantially larger than the atom size; a large (small) |ascatt| implies strong (weak) interactions. The ascatt can be systematically changed by applying an external magnetic field B to tune the atom coupling in the vicinity of a Feshbach resonance8. A fast B sweep can then jump the system from weak to strong interactions on a timescale much faster than the three-atom loss9 and thermalization. Figure 1 illustrates how an abrupt change in ascatt changes atoms’ sphere of influence, with radius ascatt, from weak to strong interaction at time t=0. The strongest interaction is found at so-called unitarity7,10 where ascatt diverges. Unitarity can be detrimental for the BEC because atoms can then scatter over large distances, as indicated by the overlapping spheres. Fast changes in ascatt have been shown to induce, for example, Sakharov oscillations11 and Bogoliubov excitations12,13,14.
An important milestone was reached in the fast-sweep experiment by Makotyn et al.15 (f-s experiment) with a 85Rb BEC swept to unitarity in just 5 μs. Beating the expectations16,17, the BEC survived the sudden jump to unitarity by evolving into a new quasiequilibrium in roughly 100 μs, which was much faster than the three-body loss rate. Earlier analyses of the f-s experiment identified a two18- and three19-body contact in the high-momentum tail of an atom distribution, which explained13,20 the momentum-dependent relaxation of the distribution tail, and assigned9 the unexpectedly long lifetime of the BEC at unitarity to a long-lived three-body state. In addition, the possibility of observing coherent oscillations has been predicted21 in an interacting Bose gas. Using full many-body computations22,23,24,25, I show that the f-s experiment has also established another landmark—coherent quantum depletion dominated by atom-cluster excitations resembling ultrafast excitations in semiconductors23,26,27.
Results
Atom-cluster dynamics in quantum depletion
Conceptually, an abrupt change in ascatt brings the BEC to a non-equilibrium in the same manner as an ultrafast laser excites solids23,26 or molecules28 to a non-equilibrium state. Ultrafast spectroscopy is renown for exciting both transient coherences22,26,29 and relaxation oscillations27 towards equilibrium. Therefore, one may expect that the f-s experiment accessed very similar effects. In semiconductors, ultrafast lasers can also excite a family of quasiparticles ranging from individual electrons and holes to correlated particle clusters25 such as the dropleton30. Analogously, it clearly is interesting to explore what kind of many-body states the f-s experiment has excited.
Solving fast-sweep generated excitations is challenging because a full quantum-kinetic description must resolve how interactions break up the BEC atoms, clustered to all orders25, into normal-component atoms that typically form independent clusters containing only few atoms. I apply a cluster-expansion approach22,23 in the excitation picture25. The BEC is then presented completely and exactly25 in terms of few atom clusters generated into the normal component; the approach is summarized in Supplementary Notes 1–4. Especially, both quantum-depletion and ultrafast semiconductor excitations share exactly the same cluster-dynamics structure where clusters are generated sequentially23,24 from small to large ones. I utilize this fundamental connection to systematically determine both the formally exact atom-cluster dynamics and a systematic truncation scheme, presented in Supplementary Note 1.
The coherence itself is identified by the transition amplitude  to move two BEC atoms into the normal component. Microscopically,
to move two BEC atoms into the normal component. Microscopically,  removes two atoms from the BEC and
removes two atoms from the BEC and  is the usual boson-creation operator for a normal-component atom with a wave vector k≠0. For large atom traps, the momentum of the BEC atoms vanishes such that
is the usual boson-creation operator for a normal-component atom with a wave vector k≠0. For large atom traps, the momentum of the BEC atoms vanishes such that  conserves the momentum by creating the atoms to momenta +ħ k and −ħ k. The accumulation of the normal component is determined by the atom occupation
conserves the momentum by creating the atoms to momenta +ħ k and −ħ k. The accumulation of the normal component is determined by the atom occupation  .
.
In the excitation picture25,24, fk and sk define the relevant two-atom clusters excited by the coherent quantum depletion. To focus the analysis on the possible coherent effects, I assume that the atom trap is closed, preventing thermalization because energy and particle exchange out of the trap is excluded. Consequently, the BEC atom number  is the difference of total atom number
is the difference of total atom number  and the number of atoms in the normal component. The resulting (sk, fk, NC) group forms a closed set of two-particle cluster dynamics, constituting the hyperbolic Bloch equations (HBEs)24. As demonstrated in Supplementary Note 4, the HBEs describe gapless BEC excitations also at unitarity and the total atom distribution becomes
and the number of atoms in the normal component. The resulting (sk, fk, NC) group forms a closed set of two-particle cluster dynamics, constituting the hyperbolic Bloch equations (HBEs)24. As demonstrated in Supplementary Note 4, the HBEs describe gapless BEC excitations also at unitarity and the total atom distribution becomes

when no distinction is made between the BEC (k=0) and normal-component atoms.
Connection of ultrafast semiconductor and BEC excitations
The HBEs resemble the semiconductor Bloch equations27,31 (SBEs) describing how ultrafast lasers drive coherent semiconductor polarization and the quantum kinetics22,23 that follows it, cf. Supplementary Note 2. In the HBEs, the coherent sk is analogously driven by a Vk NC source containing the Fourier transformation Vk of the pairwise atom–atom interaction. In analogy to the SBEs, the Vk NC source is renormalized by a ∑k′Vk′−ksk′ sum that describes the possibility of forming bound atom pairs called dimers7. Furthermore, Vk yields a hierarchical coupling to three- and four-atom-cluster dynamics, which introduces, for example, dephasing and energy shift to sk (ref. 24). Three-atom-cluster dynamics also contains the possibility of forming Efimov trimers24,32.
Since atomic BECs and semiconductors are physically very different, it is clear that HBEs and SBEs yield also distinct differences. For example, the SBEs describe the dynamics of two kinds of fermions—electrons and holes—with different effective masses, which often produces different dynamics for the respective distributions; the HBEs used contain only one class of density distributions. The fermion character itself appears in the SBEs as Pauli blocking of transitions, contrasted by the bosonic stimulation in the HBEs. At the same time, Vk is a long-range interaction in the SBEs, whereas it has a short range in an atomic Bose gas. The long range and magnitude of Vk drives the relevant interaction timescales of the SBEs to be much faster (ultrafast sub-ps scale) than in the HBEs (μs scale).
In general, the semiconductors exhibit more possibilities of binding clusters due to stronger interactions and participation of more particles classes. Nevertheless, the cluster classes and phenomenology are often strikingly similar. For example, recently found dropletons30 emerge close to the pair-ionization threshold (corresponding to unitarity), have quantized energy and are spatially extended clusters with more than three electron—hole pairs. Similar to Efimov trimers, the dropleton is significantly larger (roughly 20 times) than a bound electron—hole pair, while its energy scaling is different.
Most important, the sk drives coherent quantum depletion in the same way as the polarization embodies the coherences of the ultrafast semiconductor excitations. In semiconductors, the polarization determines the extent, symmetries and timescales of ultrafast excitations, whereas higher-order clusters, such as the dropletons, modify ‘only’ the quantitative details33. Since including additional hierarchical levels in the SBEs is numerically tedious, systematic and accurate methods have been developed to reduce it to few-parameter scattering models22 that satisfy the essential symmetries. Analogously, sk dynamics must determine central aspects of the coherent quantum depletion, whereas the formation of, for example, Efimov trimers should yield ‘only’ quantitative modifications. When the hierarchical coupling is reduced to a dephasing γ and an energy-renormalization constant μ for sk, it must24 be accompanied by an excitation-dependent relaxation for the fk, based on symmetry; the explicit systematic model is presented in Supplementary Note 2.
The capabilities of this level HBEs is thoroughly tested by matching the computational parameters exactly with the conditions of the f-s experiment as given in ref. 15. The atom mass is that of 85Rb, the spherical trap has  atoms and the average density is ‹ρ›=5.5 μm−3. The interaction is ramped from weak (ascatt=150 a0, a0 being the hydrogen Bohr radius) to unitarity (ascatt=∞) within 5 μs, which leaves γ and μ as the only free parameters chosen to match frequencies 0.761 and 0.475 kHz, respectively. The f-s experiment recorded the column distribution,
atoms and the average density is ‹ρ›=5.5 μm−3. The interaction is ramped from weak (ascatt=150 a0, a0 being the hydrogen Bohr radius) to unitarity (ascatt=∞) within 5 μs, which leaves γ and μ as the only free parameters chosen to match frequencies 0.761 and 0.475 kHz, respectively. The f-s experiment recorded the column distribution,

which is the marginal distribution of all atoms. In the f-s experiment,  was broadened15 below k=3 μm−1 and included in the computations by using a broadened BEC distribution
was broadened15 below k=3 μm−1 and included in the computations by using a broadened BEC distribution  to replace NC δk,0 in equation (1) with klim=1.1342 μm−1.
to replace NC δk,0 in equation (1) with klim=1.1342 μm−1.
Quantum kinetics of quantum depletion
Figure 2a presents  of the HBE computations for the same times as those recorded in the f-s experiment (Fig. 2 in ref. 15) where t is the evolution time at unitarity. At t=0 (shaded area),
of the HBE computations for the same times as those recorded in the f-s experiment (Fig. 2 in ref. 15) where t is the evolution time at unitarity. At t=0 (shaded area),  peaks at the origin because the system is still dominated by the BEC formed at the regime of weak interactions. Already t=15 μs evolution at unitarity (dashed line) produces an extended tail in
peaks at the origin because the system is still dominated by the BEC formed at the regime of weak interactions. Already t=15 μs evolution at unitarity (dashed line) produces an extended tail in  . After that, the tail becomes steeper and evolves towards a steady state, while the BEC peak drops significantly. One also observes that the steady state is reached faster at high momenta (roughly above k=15 μm−1) while residual deviations remain in the vicinity of k=5 μm−1, even 170 μs after the switch is on. As shown in Supplementary Note 5, this computation explains quantitatively (γ and μ being the only free parameters) the f-s experiment timescales, overall excitation levels and distribution shapes, which confirms that the f-s experiment is indeed dominated by the coherent quantum depletion. To explain more quantitative details, one also needs to include the excitation-induced effects22,33,34,35,36,37 beyond a constant μ, as shown later.
. After that, the tail becomes steeper and evolves towards a steady state, while the BEC peak drops significantly. One also observes that the steady state is reached faster at high momenta (roughly above k=15 μm−1) while residual deviations remain in the vicinity of k=5 μm−1, even 170 μs after the switch is on. As shown in Supplementary Note 5, this computation explains quantitatively (γ and μ being the only free parameters) the f-s experiment timescales, overall excitation levels and distribution shapes, which confirms that the f-s experiment is indeed dominated by the coherent quantum depletion. To explain more quantitative details, one also needs to include the excitation-induced effects22,33,34,35,36,37 beyond a constant μ, as shown later.
(a) Computed column distributions (2) for five representative t. (b) The corresponding actual nk distributions. The interactions are switched to unitarity at t=0 and homogeneous 85Rb-atom density is ρ=5.5 μm−3. (c) Normal-component fraction for two representative ρ. The vertical lines identify the snapshots analysed in a,b with matching colour coding.
The computed  also exhibits slight oscillations for 100 μs (black line) and 170 μs (red line), which seem to be only indicative in the f-s experiment; this minor difference is probably related to the experimental resolution. The actual nk distribution is plotted as in Fig. 2b using a very narrow klim=0.3781 μm−1 for the BEC. A clear BEC peak is observed in nk for all times, which shows that the BEC indeed exists even at unitarity, and that nk and
also exhibits slight oscillations for 100 μs (black line) and 170 μs (red line), which seem to be only indicative in the f-s experiment; this minor difference is probably related to the experimental resolution. The actual nk distribution is plotted as in Fig. 2b using a very narrow klim=0.3781 μm−1 for the BEC. A clear BEC peak is observed in nk for all times, which shows that the BEC indeed exists even at unitarity, and that nk and  resemble each other. The projection in equation (2) simply smoothens the oscillatory features.
resemble each other. The projection in equation (2) simply smoothens the oscillatory features.
The level of quantum depletion is defined by the fraction of normal-component atoms  , presented in Fig. 2b as function of time for ρ=5.5 μm−3 (line); the vertical lines identify the
, presented in Fig. 2b as function of time for ρ=5.5 μm−3 (line); the vertical lines identify the  snapshots of Fig. 2a. For comparison, FN is also shown for ρ=22 μm−3 (shaded area). As a general trend, FN increases as ρ becomes larger. However, the coherent quantum depletion cannot completely exhaust the BEC (NC→0) because the Vk NC source would become zero, which would reverse the coherent quantum depletion not sustained by its source. Instead, the steady-state FN saturates towards 50% for large atom densities, for example, ρ=22 μm−3 yields pronounced relaxation oscillations towards 50% after peaking FN to 72%. Also the ρ=5.5 μm−3 case shows some relaxation oscillations, but with a very long oscillation period.
snapshots of Fig. 2a. For comparison, FN is also shown for ρ=22 μm−3 (shaded area). As a general trend, FN increases as ρ becomes larger. However, the coherent quantum depletion cannot completely exhaust the BEC (NC→0) because the Vk NC source would become zero, which would reverse the coherent quantum depletion not sustained by its source. Instead, the steady-state FN saturates towards 50% for large atom densities, for example, ρ=22 μm−3 yields pronounced relaxation oscillations towards 50% after peaking FN to 72%. Also the ρ=5.5 μm−3 case shows some relaxation oscillations, but with a very long oscillation period.
The ρ dependence of relaxation oscillations is studied in Fig. 3a by comparing the peak FN (dashed line) with the final FN (red-solid line) evaluated at t=700 μs; the vertical lines identify the densities of Fig. 2b. The final FN saturates towards 50% from below at high densities, which shows that the coherent quantum depletion cannot collapse the BEC at the unitarity. For low densities, the peak and final FN are identical while they deviate significantly above ρ=10 μm−3 due to the relaxation oscillations. Even though the f-s experiment does not show pronounced relaxation oscillations, they should become visible when ρ is increased by a factor of two.
(a) Peak (dashed line) and final (solid line, t=700 μs) fraction FN of normal-component atoms generated by quantum depletion as function of density. The vertical lines indicate the densities analysed in b,c and Fig. 2. (b) Quantum kinetics of normal-component distribution for (b) ρ=5.5 μm−3 and (c) ρ=22 μm−3; the white line shows the shape of the final fk at t=700 μs.
Shell-state formation
Quantum kinetics of normal-component fk is presented in Fig. 3b,c as function of t for ρ=5.5 and 22 μm−3, respectively. The final distribution is indicated by the white line. Just after the switch is on (t=0), fk is excited to large momenta and then focuses towards the origin, as in Fig. 2a. For ρ=5.5 μm−3, fk evolves smoothly towards a monotonically decaying steady-state distribution. For ρ=22 μm−3, fk dynamics does not only show the relaxation oscillations but it approaches an unexpected form; fk peaks roughly at k=2.8 μm−1 and not at the origin. In other words, the normal-component atoms prefer to occupy a shell around the BEC due to the coherent sk; I will call this many-body configuration a shell state.
As validity checks, I show in Supplementary Note 4 that the shell state survives three-body loss, the excitation energies are indeed gapless and the results depend only slightly on the atom-trap density profile when the excitation-induced μ-shift moves the position of the shell state as function of density. Supplementary Note 3 also shows analytically that the shell state limits the coherently driven FN to 50%. Therefore, the coherent quantum depletion alone cannot annihilate the BEC—one needs additional losses38,39 or thermalization to execute that. The unexpected survival of the BEC in the f-s experiment15 was assigned to build-up of long-living (1 ms) Efimov states9. The presented results also demonstrate that the BEC is additionally shielded by the shell state. The presence of the identified coherences is also expected to reduce the losses, as shown for semiconductors33.
The spatial extent of quantum depletion can be determined by analysing the atom–atom pair correlation function g(r) that defines the normalized probability of finding an atom at position r when another one is held at the origin. The normalization is chosen to produce g(r)=1 for uncorrelated atoms, and r2(g(r)−1) determines deviations with a radial weight, as discussed in Supplementary Note 3. Figure 4 shows the r2(g(r)−1) dynamics for ρ=5.5 μm−3 in Fig. 4a and ρ=22 μm−3 in Fig. 4b, studied also in Fig. 3b and Fig. 3c, respectively. Switching to unitarity at t=0 excites a long-range order extending beyond 4 μm and shows rapid oscillations that are typical for a liquid40 where atoms are arranged into shells. At later times, the atom–shell separation increases, indicated by the fan-like expansion of the peaks and dips. In addition, the height of large-distance shells diminishes leaving only one dominant peak and dip for ρ=5.5 μm−3, indicating transition to a short-range order. For ρ=22 μm−3, the steady-state r2(g(r)−1) has about three clear peaks and dips separated roughly by 2.1 μm matching well with the 2.2-μm wave length predicted to be the shell-state peak in fk. Therefore, the relaxation observed in Figs 2 and 3 is connected with coherent quantum kinetics from long-range-order liquid to a short-range-order configuration whose range can be extended by forming the shell state.
Excitation-induced effects
To determine how quantitatively the computations already reproduce the f-s experiment, Fig. 5 compares  of the f-s experiment (filled circles) with the constant-(μ,γ) computation (solid line). When the column distribution is multiplied by k3, the so-called two-body contact19,41,42 is observed as an asymptotically constant
of the f-s experiment (filled circles) with the constant-(μ,γ) computation (solid line). When the column distribution is multiplied by k3, the so-called two-body contact19,41,42 is observed as an asymptotically constant  . A similar asymptotic behaviour is expected in the actual k4nk distribution when multiplier k4 is used instead of k3 due to dimensionality difference of nk and
. A similar asymptotic behaviour is expected in the actual k4nk distribution when multiplier k4 is used instead of k3 due to dimensionality difference of nk and  .
.
Figure 5 shows that the constant-(μ,γ) computation already explains the experiment in great detail for the early times. However, it slightly underestimates nk and  at late times, close to k=7 μm−1. Such quantitative differences are not unexpected because the excitation-induced shift (EIS) in μ and the excitation-induced dephasing (EID) in γ should modify the quantitative distribution/spectral shapes, as in semiconductors33.
at late times, close to k=7 μm−1. Such quantitative differences are not unexpected because the excitation-induced shift (EIS) in μ and the excitation-induced dephasing (EID) in γ should modify the quantitative distribution/spectral shapes, as in semiconductors33.
To verify this explanation, I have also performed EIS computations that include the three-body loss, main features of EID/EIS and calculated the distributions using a local density approximation (LDA) average; details are given in Supplementary Note 5. Both EIS and EID are generated by the hierarchical coupling to three- and four-atom clusters that are induced by nonlinear source terms containing products of fk and sk. As shown in ref. 24, such sources yield at least a quadratic density dependence for both γ and μ, in analogy to the three-body loss. To capture these excitation-induced aspects, I use the simplest functional form μ=211.4 Hz+628.9(ρn/μm−3)2Hz and γ=21.14 Hz+10.48(ρn/μm−3)2Hz, where ρn is the density of normal-component atoms. Many combinations of constant and quadratic coefficients produce qualitatively similar  results; the used specific values yield roughly the best quantitative agreement with the experiment. The three-body loss model is defined in Supplementary Note 4 and its time constant is chosen to produce a 630-μs decay at ‹ρ›=5.5 μm−3, as in the experiment15. Owing to density dependence of the three-atom loss, μ and γ, the shape of
results; the used specific values yield roughly the best quantitative agreement with the experiment. The three-body loss model is defined in Supplementary Note 4 and its time constant is chosen to produce a 630-μs decay at ‹ρ›=5.5 μm−3, as in the experiment15. Owing to density dependence of the three-atom loss, μ and γ, the shape of  depends so strongly on the local density that the LDA average of Supplementary Note 4 needs to be implemented for a precise comparison.
depends so strongly on the local density that the LDA average of Supplementary Note 4 needs to be implemented for a precise comparison.
The shaded areas in Fig. 5 present the LDA-averaged  of the EIS/EID computation. At early times (t=15 μs), the EIS/EID and constant-(μ, γ) computation (solid line) distributions are essentially the same, both explaining the experiment very well. However, only the EIS/EID computation agrees with the experiment quantitatively at t=100 μs. In other words, this analysis verifies that the quantitative deviations between the experiment and constant-(μ, γ) computation stem from the excitation-induced effects. Both computations explain the presence of weak oscillations in the experiment as relaxation oscillations. While the oscillation period agrees well, there are some differences in the experimental versus theoretical oscillation amplitude. However, the deviation is close to the experimental noise level such that one would need to measure these oscillations with a finer resolution and probably compute the excitation-induced effects fully quantum kinetically to explain all quantitative details; both studies are beyond the scope of the present investigation.
of the EIS/EID computation. At early times (t=15 μs), the EIS/EID and constant-(μ, γ) computation (solid line) distributions are essentially the same, both explaining the experiment very well. However, only the EIS/EID computation agrees with the experiment quantitatively at t=100 μs. In other words, this analysis verifies that the quantitative deviations between the experiment and constant-(μ, γ) computation stem from the excitation-induced effects. Both computations explain the presence of weak oscillations in the experiment as relaxation oscillations. While the oscillation period agrees well, there are some differences in the experimental versus theoretical oscillation amplitude. However, the deviation is close to the experimental noise level such that one would need to measure these oscillations with a finer resolution and probably compute the excitation-induced effects fully quantum kinetically to explain all quantitative details; both studies are beyond the scope of the present investigation.
Discussion
Quantum depletion can be partially described in terms of the Bogoliubov excitations24, but they alone destroy the BEC at high densities13 because one needs the shell state to shield the BEC. The HBEs include the Bogoliubov excitations as a substructure24, while the shell state as well as dimers result from the additional coupling among them. In fact, the coherent quantum depletion drives many dimer resonances, especially just after the jump to unitarity, based on the time–energy uncertainty. All of the initially generated dimer components in sk evolve with their own eigen frequency, which generates quantum beats as the system evolves further, explaining the observed nk oscillations and the transient long-range order. The relaxation oscillations appear through the nonlinear modulation in the quantum-depletion source.
The presented quantum-kinetic theory explains how an atomic BEC generates the normal component via sequential atom clustering when the atom–atom interactions are switched fast to unitarity. The resulting kinetics is initiated by a transition amplitude describing a coherent ejection of two BEC atoms to the normal component. This process is shown to explain the recent f-s experiment15 in great detail, which connects quantum depletion with coherent non-equilibrium processes in semiconductors.
The coherent quantum depletion identified should exhibit partial reversibility when switched back to weak interactions. Coherent control should also become possible when a sequence of Feshbach-resonance modulations is implemented. For atom densities that are roughly two times higher than in the Makotyn et al.15 experiment, the coherent quantum-depletion process is shown to form a shell state faster than 50 μs even when three-body losses are present, which prevents quantum depletion beyond 50% normal-component fraction at quasiequilibrium.
The identification of the shell state is simplest if one can experimentally access the normal-component distribution fk of a homogeneous density. However, current measurements detect the overall distribution nk including both the BEC and the normal component, and measure its density average. In a realistic experiment, the BEC contribution of nk spreads around k=0 due to finite-size effects15. The visibility of the shell state can, therefore, be enhanced by decreasing the BEC spreading and/or by having a flatter atom trap, which makes the density profile more homogeneous. Therefore, further experiments and/or analyses are needed for an unambiguous identification of the shell state. The computations suggest that the shell state should become appreciable at atom densities that are roughly two times higher than in ref. 15, and that the excitation-induced effects can be accessed by comparing experiment and theory  distributions quantitatively; an analogous analysis has delivered very precise insights into the many-body states involved in semiconductor excitations33.
distributions quantitatively; an analogous analysis has delivered very precise insights into the many-body states involved in semiconductor excitations33.
The predicted non-equilibrium dynamics as well as shell-state formation can be experimentally accessed by measuring the evolution of atom distribution nk, which also provides direct information of the normal-component fraction and its shape. I also expect that the effect of higher-order clusters (such as Efimov trimers) can be identified through quantitative shape changes in the nk, in analogy to the cluster-based studies in semiconductors30,33. Experiments with multiple switch-on/off sequences may access analogous coherent non-equilibrium quantum kinetics as in ultrafast semiconductor excitations. Through this connection, one may extend the future fast-sweep experiments to utilize novel concepts such as coherent control43 and quantum spectroscopy30,44,45 to access unexpected many-body states.
Methods
General aspects
Coherent quantum depletion is solved with the HBEs24 that establish a new method to study an interacting Bose gas. The HBEs are presented in Supplementary Note 1 while the actual cluster-expansion22,23 derivation is performed in ref. 24. The HBEs are analogous to the SBEs that govern the physics of ultrafast excitations in semiconductors22,23,27. Using the formal HBE–SBE connection, the quantum-kinetics insights of semiconductor studies are applied to reduce the hierarchical many-body coupling to a dephasing and energy shift that conserve the energy and maintain the BEC excitation as a minimum uncertainty state of the Heisenberg uncertainty relation. At this level, the method studies exclusively coherent quantum depletion because it deliberately omits atom loss, energy loss and thermalization. Atom losses can be included straightforwardly as explained in Supplementary Note 4.
Numerical aspects
The HBEs couple the coherent transition amplitude sk with the normal component and BEC occupations fk and NC, respectively. Owing to the radial symmetry, one needs to consider only the radial k dependency for both sk and fk. The resulting HBE computations are performed by discretizing k into 800 intervals and the atom–atom interactions are modelled with a realistic Morse potential. In order to resolve both the short- and long-range quantum kinetics of the interacting atoms, the k grid is divided into two parts: the low-k grid extends up to 76 μm−1 and the high-k grid reaches 6.0 × 104 μm−1, both containing 400 points. This grid covers k values for over 5 orders of magnitude, which is sufficient to reveal how the atom–atom interactions exhibit repulsion <100 pm and unitarity interaction extending to macroscopic distances. The HBE dynamics is then solved with a fourth-order Runge–Kutta method.
Additional information
How to cite this article: Kira, M. Coherent quantum depletion of an interacting atom condensate. Nat. Commun. 6:6624 doi: 10.1038/ncomms7624 (2015).
References
Raimond, J. M., Brune, M. & Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 73, 565–582 (2001) .
Khitrova, G., Gibbs, H. M., Kira, M., Koch, S. W. & Scherer, A. Vacuum Rabi splitting in semiconductors. Nat. Phys. 2, 81–90 (2006) .
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008) .
Gardiner, C. W., Lee, M. D., Ballagh, R. J., Davis, M. J. & Zoller, P. Quantum kinetic theory of condensate growth: comparison of experiment and theory. Phys. Rev. Lett. 81, 5266–5269 (1998) .
Xu, K. et al. Observation of strong quantum depletion in a gaseous Bose—Einstein condensate. Phys. Rev. Lett. 96, 180405 (2006) .
Wüster, S. et al. Quantum depletion of collapsing Bose—Einstein condensates. Phys. Rev. A 75, 043611 (2007) .
Giorgini, S., Pitaevskii, L. & Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 80, 1215–1274 (2008) .
Chin, C., Grimm, R., Julienne, P. & Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 82, 1225–1286 (2010) .
Sykes, A. G. et al. Quenching to unitarity: quantum dynamics in a three-dimensional Bose gas. Phys. Rev. A 89, 021601 (2014) .
Braaten, E. & Hammer, H.-W. Universality in few-body systems with large scattering length. Phys. Rep. 428, 259–390 (2006) .
Hung, V., Gurarie, C.-L. & Chin, C. From cosmology to cold atoms: observation of Sakharov oscillations in a quenched atomic superfluid. Science 341, 1213–1215 (2013) .
Natu, S. & Mueller, E. Dynamics of correlations in a dilute Bose gas following an interaction quench. Phys. Rev. A 87, 053607 (2013) .
Yin, X. & Radzihovsky, L. Quench dynamics of a strongly interacting resonant Bose gas. Phys. Rev. A 88, 063611 (2013) .
Kain, B. & Ling, H. Y. Nonequilibrium states of a quenched Bose gas. Phys. Rev. A 90, 063626 (2014) .
Makotyn, P., Klauss, C., Goldberger, D., Cornell, E. & Jin, D. Universal dynamics of a degenerate unitary Bose gas. Nat. Phys. 10, 116–119 (2014) .
Papp, S. B. et al. Bragg spectroscopy of a strongly interacting Rb85 Bose–Einstein condensate. Phys. Rev. Lett. 101, 135301 (2008) .
Navon, N. et al. Dynamics and thermodynamics of the low-temperature strongly interacting Bose gas. Phys. Rev. Lett. 107, 135301 (2011) .
Corson, J. & Bohn, J. Bound-state signatures in quenched Bose—Einstein condensates. Phys. Rev. A 91, 013616 (2014) .
Smith, D., Braaten, E., Kang, D. & Platter, L. Two-body and three-body contacts for identical bosons near unitarity. Phys. Rev. Lett. 112, 110402 (2014) .
Rançon, A. & Levin, K. Equilibrating dynamics in quenched Bose gases: characterizing multiple time regimes. Phys. Rev. A 90, 021602 (2014) .
Holland, M., Park, J. & Walser, R. Formation of pairing fields in resonantly coupled atomic and molecular Bose—Einstein condensates. Phys. Rev. Lett. 86, 1915–1918 (2001) .
Kira, M. & Koch, S. W. Many-body correlations and excitonic effects in semiconductor spectroscopy. Prog. Quant. Electron. 30, 155–296 (2006) .
Kira, M. & Koch, S. W. Semiconductor Quantum Optics 1st edn Cambridge University Press (2011) .
Kira, M. Hyperbolic Bloch equations: atom-cluster kinetics of an interacting Bose gas. Preprint at http://arxiv.org/abs/1407.4927 (2014) .
Kira, M. Excitation picture of an interacting Bose gas. Ann. Phys. 351, 200–249 (2014) .
Shah, J. Ultrafast Spectroscopy of Semiconductors and Semiconductor Nanostructures 2nd edn Springer (1999) .
Haug, H. & Koch, S. Quantum Theory of the Optical and Electronic Properties of Semiconductors 5th edn World Scientific (2009) .
Zewail, A. Laser femtochemistry. Science 242, 1645–1653 (1988) .
Chemla, D. & Shah, J. Many-body and correlation effects in semiconductors. Nature 411, 549–557 (2001) .
Almand-Hunter, A. et al. Quantum droplets of electrons and holes. Nature 506, 471–475 (2014) .
Lindberg, M. & Koch, S. W. Effective bloch equations for semiconductors. Phys. Rev. B 38, 3342–3350 (1988) .
Hammer, H.-W., Nogga, A. & Schwenk, A. Colloquium: three-body forces: from cold atoms to nuclei. Rev. Mod. Phys. 85, 197–217 (2013) .
Smith, R. P. et al. Extraction of many-body configurations from nonlinear absorption in semiconductor quantum wells. Phys. Rev. Lett. 104, 247401 (2010) .
Peyghambarian, N. et al. Blue shift of the exciton resonance due to exciton-exciton interactions in a multiple-quantum-well structure. Phys. Rev. Lett. 53, 2433–2436 (1984) .
Wang, H. et al. Transient nonlinear optical response from excitation induced dephasing in gaas. Phys. Rev. Lett. 71, 1261–1264 (1993) .
Wang, H. et al. Transient four-wave-mixing line shapes: effects of excitation-induced dephasing. Phys. Rev. A 49, R1551–R1554 (1994) .
Shacklette, J. M. & Cundiff, S. T. Role of excitation-induced shift in the coherent optical response of semiconductors. Phys. Rev. B 66, 045309 (2002) .
Burt, E. A. et al. Coherence, correlations, and collisions: what one learns about Bose—Einstein condensates from their decay. Phys. Rev. Lett. 79, 337–340 (1997) .
Donley, E. et al. Dynamics of collapsing and exploding Bose—Einstein condensates. Nature 412, 295–299 (2001) .
Jorgensen, W. L., Chandrasekhar, J., Madura, J. D., Impey, R. W. & Klein, M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79, 926–935 (1983) .
Tan, S. Energetics of a strongly correlated Fermi gas. Ann. Phys. 323, 2952–2970 (2008) .
Tan, S. Large momentum part of a strongly correlated Fermi gas. Ann. Phys. 323, 2971–2986 (2008) .
Warren, W., Rabitz, H. & Dahleh, M. Coherent control of quantum dynamics: the dream is alive. Science 259, 1581–1589 (1993) .
Kira, M. & Koch, S. W. Quantum-optical spectroscopy of semiconductors. Phys. Rev. A 73, 013813 (2006) .
Kira, M., Koch, S. W., Smith, R. P., Hunter, A. E. & Cundiff, S. T. Quantum spectroscopy with Schrödinger-cat states. Nat. Phys. 7, 799–804 (2011) .
Acknowledgements
I thank Deborah Jin, JILA, for fruitful discussions about the fast-switch experiment and Renate Schmid for careful proof reading of the manuscript.
Author information
Authors and Affiliations
Contributions
M.K. is solely responsible for the scientific content of this work.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-6, Supplementary Notes 1-5 and Supplementary References (PDF 346 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kira, M. Coherent quantum depletion of an interacting atom condensate. Nat Commun 6, 6624 (2015). https://doi.org/10.1038/ncomms7624
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms7624
This article is cited by
-
Lightwave electronics in condensed matter
Nature Reviews Materials (2023)
-
On the survival of the quantum depletion of a condensate after release from a magnetic trap
Scientific Reports (2022)
-
Attosecond clocking of correlations between Bloch electrons
Nature (2022)
-
Lightwave valleytronics in a monolayer of tungsten diselenide
Nature (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.







 is compared with constant-(μ, γ) (solid line) and full EIS/EID (shaded area) HBE computations for (a) t=15 μs, (b) t=35 μs and (c) t=100 μs after switching to unitarity. The experimental points are read from the inset to
is compared with constant-(μ, γ) (solid line) and full EIS/EID (shaded area) HBE computations for (a) t=15 μs, (b) t=35 μs and (c) t=100 μs after switching to unitarity. The experimental points are read from the inset to