Abstract
Bismuth chalcogenides and lead telluride/selenide alloys exhibit exceptional thermoelectric properties that could be harnessed for power generation and device applications. Since phonons play a significant role in achieving these desired properties, quantifying the interaction between phonons and electrons, which is encoded in the Eliashberg function of a material, is of immense importance. However, its precise extraction has in part been limited due to the lack of local experimental probes. Here we construct a method to directly extract the Eliashberg function using Landau level spectroscopy, and demonstrate its applicability to lightly doped thermoelectric bulk insulator PbSe. In addition to its high energy resolution only limited by thermal broadening, this novel experimental method could be used to detect variations in mass enhancement factor at the nanoscale level. This opens up a new pathway for investigating the local effects of doping and strain on the mass enhancement factor.
Similar content being viewed by others
Introduction
The effects of interactions between electrons and phonons can be ubiquitously observed in systems ranging from simple metals1, to more exotic materials such as graphene2,3, high-temperature superconductors4,5,6,7,8,9 and topological insulators10,11,12,13,14,15,16. In general, electron–phonon interactions give rise to quasiparticles of decreased mobility and increased effective mass. This process is theoretically captured by the Eliashberg function α2F(ω;k,E) (ref. 17), which encodes the scattering of quasiparticles by coupling to a bosonic mode of frequency ω. The Eliashberg function is related to the complex self-energy of the system (Σ(k,E)) (ref. 17), an experimentally accessible quantity that contains both the quasiparticle energy shift due to interactions (Σ′(k,E)=Re{Σ(k,E)}) and its lifetime (Σ″(k,E)=Im{Σ(k,E)}). Σ′(k,E) and Σ″(k,E) are related to one another by Kramers–Kronig relations, so knowing only one of them should, in principle, be sufficient to determine the total self-energy Σ(k,E), and thus the Eliashberg function itself18. Since many fundamental properties, such as the electron mass enhancement factor (λ), can be calculated from the Eliashberg function, its precise experimental determination is of immense importance.
In topological materials, there are clear instances where electron–phonon coupling (EPC) has measurable physical effects10,19. Although relatively well described within the framework of non-interacting Dirac theory, surface state Dirac fermions in topological materials are experimentally found to interact with lattice excitations10,11,12,13,14,15,16, leading to the renormalization of the underlying surface state band structure. The role and magnitude of this interaction are still under debate, as vastly different results have been obtained not only across different techniques, but also using the same experimental probe on nominally identical compounds13,14. For example, the measured λ in a typical three-dimensional topological insulator Bi2Se3 is found to range from as low as λ~0.17 (ref. 13) (measured at 20 K) to λ~3 (ref. 14) (measured at 7 K) in recent laser-based angle-resolved photoemission spectroscopy (ARPES) studies reported by two different groups. Careful analysis by Howard and El-Batanouny showed that different acquisition temperatures (7 K vs 20 K) would account for some of the discrepancy, but only less than a factor of 2 between the two studies20. Possible reasons for this discrepancy may be the resolution of the technique or the inability to detect the 3-meV phonon peak in ref. 13, which was reported by Kondo et al.14 Another contributing factor might lie in the intrinsic structural inhomogeneity (local chemical potential variation, step-edges, defects, strain/stress, and so on) present on the surface of these materials, either as an inevitable consequence of the cleavage process or the varying sample quality. Thus, developing a high-resolution technique for local determination of EPC on nanometre length scales with simultaneous imaging of the surface and the local density of states would be of tremendous importance not only for obtaining λ with a measure of reliability, but also for a deeper understanding of the factors affecting EPC, and ultimately for measuring the Eliashberg function for interacting systems such as superconductors or charge density wave materials where the EPC plays an important role in determining their ground state.
To illustrate subtle self-energy effects present due to the interaction of phonons and electrons, let us use a single electronic band crossing the Fermi level as an example (Fig. 1). In the absence of EPC, this band is expected to smoothly cross the Fermi level. However, when EPC is turned on, an antisymmetric kink develops in the dispersion near the Fermi level. To reliably extract this band renormalization, high-resolution experimental determination of the electronic band structure is crucial. Scanning tunnelling microscopy (STM) has been successfully applied to nanoscale band structure mapping using either the method of quasiparticle interference (QPI)21,22 or Landau level (LL) spectroscopy23,24,25. In relatively simple systems such as Ag(111), QPI imaging has proven effective for the detection of small kinks in the electronic dispersion, which allowed the approximation of the electron mass enhancement λ (ref. 26). Applying the same technique to Fe-based high-temperature superconductors has revealed the momentum–space anisotropy in self-energy likely originating from antiferromagnetic spin fluctuations9. Therefore, this method could naturally be extended to other materials. However, it cannot be used in many three-dimensional topological materials as the fundamental nature of the topological surface states prohibits quasiparticle backscattering27 and therefore prevents the observation of QPI in the desired energy range28,29. Furthermore, the extracted band structure from QPI measurements is often noisier25, requires longer time acquisition and provides lower energy resolution compared with the band mapping using LL spectroscopy.
In the following, we will describe the first utilization of LL band mapping to extract the self-energy, the Eliashberg function and λ in a trivial bulk insulator Pb1-xSnxSe with x~0.09.
Results
Surface characterization
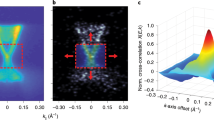
Single crystals of Pb1−xSnxSe are prepared using the self-selecting vapour growth method, cleaved at ~77 K in ultra-high-vacuum, and immediately inserted into the STM where they are held at 4 K during data acquisition. Although the process of cleaving can result in multiple surface step-edges and even distinct cleavage planes, we are able to find microscopically large, atomically flat regions characterized to be the (001) surface based on the square atomic lattice observed in STM topographs (Fig. 2a). The average conductance dI/dV spectrum, which is directly proportional to the local density of states, exhibits a clear gap of ~50 meV (Fig. 2b), confirming that this composition would be a band insulator without the intrinsic doping due to defects that moves the Fermi energy into the conduction band. Although Pb1-xSnxSe is non-topological at the alloying composition studied, it hosts distinct trivial surface states that can be observed and studied using STM30. We note here that the gap measured by us sets a lower limit for the band gap; the actual value may be larger but masked due to the surface state. We proceed to describe the utilization of LL spectroscopy to map an electronic band crossing the Fermi level for the purposes of quantifying many-body interactions.
(a) Typical STM topograph of the (001) surface showing a clear square lattice. (b) Average dI/dV spectrum obtained over the region of the sample in a, showing an integrated density of states gap of ~50 meV that sets a minimum value for the band gap at this composition. Setup conditions in: (a) Iset=10 pA, Vset=−100 mV; (b) Iset=100 pA, Vset=−100 mV.
Electronic band structure mapping using LL spectroscopy
When a magnetic field is applied perpendicular to the surface of a sample, LLs emerge as peaks in dI/dV spectra on top of the U-shaped background, which signal the quantization of the two-dimensional surface states (Fig. 3a,b). Using a semi-classical approximation, it can be shown that for an isotropic Fermi surface, the magnitude of the momentum vector (k) at any given energy E is proportional to (NB)0.5, where N is the LL index, B is the applied magnetic field and E is the energy of the LL peak. For a non-isotropic Fermi surface, the Fermi surface area is proportional to NB, which can be mapped to an effective (angle-integrated average) momentum given by (NB)0.5. In either case, this allows us to use LLs to measure the angle-integrated dispersion with high precision.
(a) Average dI/dV spectra, vertically offset for clarity, obtained at different applied magnetic fields. Each spectrum is determined by averaging 64 point-spectra, spaced equally along a 20-nm line cut across the region of the sample shown in Fig. 2a. (b) Normalized dI/dV spectra, vertically offset for clarity (see Supplementary Note 1 for normalization details). (c) Average-integrated momentum k versus bias dispersion of a single SS band crossing the Fermi level (circles) and the bare quasiparticle dispersion (red) (Supplementary Note 2). Different colours of circles indicate different LL indices. Setup condition in a are: Iset=100 pA, Vset=−100 mV.
Our first task is to plot the LL energy as a function of (NB)0.5. Since precise determination of LL peak positions is of extreme importance for our study, we normalize each dI/dV spectrum acquired in a magnetic field (Fig. 3b) before fitting a Lorentzian curve to locate the position of each LL peak (see Supplementary Fig. 1 and Supplementary Note 1). We note that this process is only possible if all dI/dV spectra are acquired over the ‘identical’ region of the sample with ‘no tip changes’. Next, we index the LLs with integer numbers as shown in Fig. 3b and plot their positions as a function of average-integrated momentum to obtain a continuous dispersion (Fig. 3c and Supplementary Fig. 2). Since the data were acquired in small magnetic field increments of 0.1 T, we are able to obtain nearly 100 data points within the narrow energy range of ±30 meV around the Fermi level. The energy resolution of our experiments is only limited by thermal broadening (~4kBT, where kB is the Boltzmann constant and T is the temperature) and is ~1.5 meV at 4 K.
Extracting the Eliashberg function and mass enhancement factor
The real part of the self-energy of the electrons Σ′(k,E) can be calculated as the difference between the measured dispersion ε(k) shown in Fig. 3c and the bare quasiparticle dispersion ε0(k) (Fig. 4a). To get a physical intuition on the bare quasiparticle dispersion, we perform tight-binding calculations on x~0.09 Pb1−xSnxSe to obtain the theoretically predicted surface state (SS) dispersion. As expected, this dispersion is nearly linear with a very small quadratic correction. It can be approximated as a second-degree polynomial in the form of ε0(k)=α(k−kf)+β(k−kf)2, where kf is the momentum wave vector at the Fermi level (Supplementary Note 2). Using coefficients α and β (adjusted by <6% to match our experimental data at energies away from the Fermi level), we can determine Σ′(k,E) (Fig. 4a). The extracted Σ′(k,E) is antisymmetric with respect to the Fermi level, with positive values for the occupied states and negative values for the unoccupied states. Σ′(k,E) and the Eliashberg function α2F(ω) are related by the integral equation:  , where
, where  and f(x) is the Fermi distribution function. The inversion of this integral to calculate α2F(ω) is mathematically unstable and results in unphysical solutions18. However, this problem can be circumvented by the application of the maximum entropy method (MEM) (ref. 18) to fit Σ′(k,E) and calculate the α2F(ω) of our system (Fig. 4b and Supplementary Notes 3 and 4). In contrast to the use of this method on real self-energy obtained from ARPES18,31, our measurements allow access to both occupied and unoccupied states, and we can use the whole energy range of these to calculate α2F(ω), thus using more information to converge to the correct α2F(ω). The mass enhancement factor λ is easily calculated from α2F(ω) as
and f(x) is the Fermi distribution function. The inversion of this integral to calculate α2F(ω) is mathematically unstable and results in unphysical solutions18. However, this problem can be circumvented by the application of the maximum entropy method (MEM) (ref. 18) to fit Σ′(k,E) and calculate the α2F(ω) of our system (Fig. 4b and Supplementary Notes 3 and 4). In contrast to the use of this method on real self-energy obtained from ARPES18,31, our measurements allow access to both occupied and unoccupied states, and we can use the whole energy range of these to calculate α2F(ω), thus using more information to converge to the correct α2F(ω). The mass enhancement factor λ is easily calculated from α2F(ω) as  . From our data in Fig. 4a, we get λ to be 0.11±0.05. Our measurements reveal weak EPC in this material, which may play a role in the high thermoelectric power observed by other techniques32. We note that surface λ measured in our experiments is comparable to the bulk λ reported on similar compounds obtained using Shubnikov–de Haas oscillations33.
. From our data in Fig. 4a, we get λ to be 0.11±0.05. Our measurements reveal weak EPC in this material, which may play a role in the high thermoelectric power observed by other techniques32. We note that surface λ measured in our experiments is comparable to the bulk λ reported on similar compounds obtained using Shubnikov–de Haas oscillations33.
To demonstrate the validity of our method, we perform the following tests. Both α2F(ω) and λ determined separately using the dispersion of the occupied electronic states (α2F−(ω); λ−) and the unoccupied states (α2F+(ω); λ+) are expected to yield identical results. To check this, we first calculate and directly compare α2F−(ω) and α2F+(ω) functions. Remarkably, these two provide an excellent match within our experimental resolution as the principle phonon modes in both are at nearly identical energies (Supplementary Fig. 3), which further confirms the high quality of our experimental data. Moreover, λ− and λ+ extracted from curves in Supplementary Fig. 3 are the same within the measurement error.
Finally, we apply our method to a second system, Bi2Se3, to search for the expected signatures of EPC (Supplementary Note 5). Although the reported magnitudes of λ in Bi2Se3 vary widely across different experiments as discussed in the introductory paragraphs, even the smallest detected λ (~0.17 in ref. 13) should in principle result in band renormalization large enough to be detected by our novel experimental method. In this endeavour, we use the data from one of the pioneering LL studies in Bi2Se3 acquired in ref. 34. The extracted SS band dispersion shows a prominent deviation from the smooth evolution noticeable near the Fermi level that clearly signals the presence of EPC (Supplementary Fig. 4a). Furthermore, by calculating the real part of the self-energy (Supplementary Fig. 4b) we determine λ to be ~0.26, which is within the range of reported values on this material. We note that although the analysis presented here on Bi2Se3 suggests EPC weaker than some of the other studies14,15,16, we cannot exclude the presence of ~3 meV peak reported by Kondo et al.14 or ~8 meV peak reported by Sobota et al.16, and higher resolution future studies may be needed. Nevertheless, the available data and analysis presented here demonstrate yet another confirmation of the validity of our methodology.
Discussion
We expect that this newly developed method of determining EPC by LL spectroscopy will be especially useful for two-dimensional systems like graphene or ultra-thin films as well as in materials where surface states play an important role in determining the electronic properties. In many topological insulators, bulk and surface state electronic bands lie close to each other in energy and momentum and disentangling the two using ARPES can be challenging. Our method provides a natural solution to this problem as the strongly kz-dispersing bulk bands would not be observed using STM, which allows us to examine the effect of phonons exclusively on the topological surface states. Furthermore, phonon modes and EPC itself are likely sensitive to the presence of inhomogeneous structural distortions, and our work provides a way to probe this. For example, ‘stripe’-like inhomogeneity in Bi2Te3 single crystals28 and surface dislocations in Bi2Se3 thin films35 have already shown to result in a prominent change in the local density of states, but the evidence of any resulting modification in the phonon spectrum is still lacking. Our new method could provide further insight into the electron–phonon dynamics in these materials at the nanoscale level and could facilitate engineering other novel systems with more desirable properties.
Additional information
How to cite this article: Zeljkovic, I. et al. Nanoscale determination of the mass enhancement factor in the lightly doped bulk insulator lead selenide. Nat. Commun. 6:6559 doi: 10.1038/ncomms7559 (2015).
References
McMillan, W. L. & Rowell, J. M. Lead phonon spectrum calculated from superconducting density of states. Phys. Rev. Lett. 14, 108–112 (1965) .
Bostwick, A., Ohta, T., Seyller, T., Horn, K. & Rotenberg, E. Quasiparticle dynamics in graphene. Nat. Phys. 3, 36–40 (2006) .
Bostwick, A. et al. Observation of plasmarons in quasi-freestanding doped graphene. Science 328, 999–1002 (2010) .
Lanzara, A. et al. Evidence for ubiquitous strong electron-phonon coupling in high-temperature superconductors. Nature 412, 510–514 (2001) .
Lee, J. et al. Interplay of electron-lattice interactions and superconductivity in superconductivity in Bi2Sr2CaCu2O8+δ . Nature 442, 546–550 (2006) .
Niestemski, F. C. et al. A distinct bosonic mode in an electron-doped high-transition-temperature superconductor. Nature 450, 1058–1061 (2007) .
Shan, L. et al. Evidence of a spin resonance mode in the iron-based superconductor Ba0.6K0.4Fe2As2 from scanning tunneling spectroscopy. Phys. Rev. Lett. 108, 227002 (2012) .
Chi, S. et al. Scanning tunneling spectroscopy of superconducting LiFeAs single crystals: evidence for two nodeless energy gaps and coupling to a Bosonic mode. Phys. Rev. Lett. 109, 087002 (2012) .
Allan, M. P. et al. Identifying the ‘fingerprint’ of antiferromagnetic spin-fluctuations in iron-pnictide Cooper pairing. Preprint at http://arxiv.org/abs/1402.3714.
Zhu, X. et al. Interaction of phonons and Dirac Fermions on the surface of Bi2Se3: a strong Kohn anomaly. Phys. Rev. Lett. 107, 186102 (2011) .
Zhu, X. et al. Electron-phonon coupling on the surface of the topological insulator Bi2Se3 determined from surface-phonon dispersion measurements. Phys. Rev. Lett. 108, 185501 (2012) .
Howard, C., El-Batanouny, M., Sankar, R. & Chou, F. C. Anomalous behavior in the phonon dispersion of the (001) surface of Bi2Te3 determined from helium atom-surface scattering measurements. Phys. Rev. B 88, 035402 (2013) .
Chen, C. et al. Tunable Dirac fermion dynamics in topological insulators. Sci. Rep. 3, 2411 (2013) .
Kondo, T. et al. Anomalous dressing of Dirac Fermions in the topological surface state of Bi2Se3, Bi2Te3, and Cu-doped Bi2Se3 . Phys. Rev. Lett. 110, 217601 (2013) .
Costache, M. V. et al. Fingerprints of inelastic transport at the surface of the topological insulator Bi2Se3: role of electron-phonon coupling. Phys. Rev. Lett. 112, 086601 (2014) .
Sobota, J. A. et al. Distinguishing bulk and surface electron-phonon coupling in the topological insulator Bi2Se3 using time-resolved photoemission spectroscopy. Phys. Rev. Lett. 113, 157401 (2014) .
Grimvall, G. The Electron-Phonon Interaction in Metals (Selected Topics in Solid State Physics XVI) Elsevier Science Ltd (1981) .
Shi, J. et al. Direct extraction of the Eliashberg function for electron-phonon coupling: a case study of . Phys. Rev. Lett. 92, 186401 (2004) .
Delaire, O. et al. Giant anharmonic phonon scattering in PbTe. Nat. Mater. 10, 614–619 (2011) .
Howard, C. & El-Batanouny, M. Connecting electron and phonon spectroscopy data to consistently determine quasiparticle-phonon coupling on the surface of topological insulators. Phys. Rev. B 89, 075425 (2014) .
Hoffman, J. E. et al. Imaging quasiparticle interference in Bi2Sr2CaCu2O8+δ . Science 297, 1148–1151 (2002) .
McElroy, K. et al. Relating atomic-scale electronic phenomena to wave-like quasiparticle states in superconducting Bi2Sr2CaCu2O8+δ . Nature 422, 592–596 (2003) .
Hashimoto, K. et al. Quantum Hall transition in real space: from localized to extended states. Phys. Rev. Lett. 101, 256802 (2008) .
Li, G. & Andrei, E. Y. Observation of Landau levels of Dirac fermions in graphite. Nat. Phys. 3, 623–627 (2007) .
Soumyanarayanan, A. et al. Imaging the nanoscale band structure of topological Sb. Preprint at http://arxiv.org/abs/1311.1758.
Grothe, S. et al. Quantifying many-body effects by high-resolution Fourier transform scanning tunneling spectroscopy. Phys. Rev. Lett. 111, 246804 (2013) .
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010) .
Okada, Y. et al. Ripple-modulated electronic structure of a 3D topological insulator. Nat. Commun. 3, 1158 (2012) .
Zhang, T., Levy, N., Ha, J., Kuk, Y. & Stroscio, J. A. Scanning tunneling microscopy of gate tunable topological insulator Bi2Se3 thin films. Phys. Rev. B 87, 115410 (2013) .
Zeljkovic, I. et al. Dirac mass generation from crystal symmetry breaking on the surfaces of topological crystalline insulators. Nat. Mater. 14, 318–324 (2015) .
Zhou, X. et al. Multiple Bosonic mode coupling in the electron self-energy of (La2-xSrx)CuO4 . Phys. Rev. Lett. 95, 117001 (2005) .
Wang, H., Pei, Y., LaLonde, A. D. & Snyder, G. J. Weak electron-phonon coupling contributing to high thermoelectric performance in n-type PbSe. Proc. Natl Acad. Sci. USA 109, 9705–9709 (2012) .
Yusheng, H., Grassie, A. D. C. & Hong-Chang, F. The variation of the electron-phonon mass enhancement through the structural phase transition. J. Phys. F Met. Phys. 15, 877–882 (1985) .
Cheng, P. et al. Landau quantization of topological surface states in Bi2Se3 . Phys. Rev. Lett. 105, 076801 (2010) .
Liu, Y. et al. Tuning Dirac states by strain in the topological insulator Bi2Se3 . Nat. Phys. 10, 294–299 (2014) .
Acknowledgements
V.M. gratefully acknowledges funding from the US Department of Energy, Scanned Probe Division under award number DE-FG02-12ER46880 for the support of I.Z., K.L.S., Y.O., W.Z. and D.W. for this project. Z.W. acknowledges the DOE, Office of Science, Basic Energy Sciences grants DE-SC0002554 and DE-FG02-99ER45747. H.L. acknowledges the Singapore National Research Foundation under NRF award number NRF-NRFF2013-03. F.C. acknowledges the support provided by MOST-Taiwan under project number NSC-102-2119-M-002-004. The work at Northeastern University is supported by the US Department of Energy grant number DE-FG02-07ER46352 and benefited from Northeastern University’s Advanced Scientific Computation Center (ASCC) and the allocation of time at the NERSC supercomputing centre through DOE grant number DE-AC02-05CH11231.
Author information
Authors and Affiliations
Contributions
I.Z., Y.O., D.W., Z.W. and V.M. designed the experiments. STM experiments were carried out by I.Z., D.W. and W.Z. I.Z., K.L.S., D.W., Z.W. and V.M. analysed the data and wrote the paper. F.C. and R.S. contributed to the single crystal growth and structural analysis. H.L. and A.B. supervised the band structure calculations, which was performed by G.C., Y.J.W. and H.L.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-4, Supplementary Table 1, Supplementary Notes 1-5, and Supplementary References (PDF 812 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Zeljkovic, I., Scipioni, K., Walkup, D. et al. Nanoscale determination of the mass enhancement factor in the lightly doped bulk insulator lead selenide. Nat Commun 6, 6559 (2015). https://doi.org/10.1038/ncomms7559
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms7559
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.