Abstract
Stimulated Brillouin scattering is a fundamental interaction between light and travelling acoustic waves and arises primarily from electrostriction and photoelastic effects, with an interaction strength several orders of magnitude greater than that of other relevant non-linear optical processes. Here we report an experimental demonstration of Brillouin-scattering-induced transparency in a high-quality whispering-gallery-mode optical microresonantor. The triply resonant Stimulated Brillouin scattering process underlying the Brillouin-scattering-induced transparency greatly enhances the light–acoustic interaction, enabling the storage of light as a coherent, circulating acoustic wave with a lifetime up to 10 μs. Furthermore, because of the phase-matching requirement, a circulating acoustic wave can only couple to light with a given propagation direction, leading to non-reciprocal light storage and retrieval. These unique features establish a new avenue towards integrated all-optical switching with low-power consumption, optical isolators and circulators.
Similar content being viewed by others
Introduction
Stimulated Brillouin Scattering (SBS) in fibres and waveguides has attracted strong interest in a variety of photonic applications during past decades1,2, such as light storage3, slow light4,5, lasers6 and optical isolators7,8. SBS can be incorporated into photonic integrated circuits9, where the tight confinement of the optical fields greatly enhances the SBS interaction10. Giant enhancement of SBS in the subwavelength scales due to radiation pressures or boundary-induced non-linearities has been demonstrated recently10,11. SBS has also been realized in optical microresonators, such as silica microspheres12 and disks13, crystalline cylinders14. In these whispering gallery resonators, optical and acoustic waves circulate along the equatorial surface, forming optical and mechanical whispering-gallery modes (WGMs) with ultrahigh-quality (Q) factor. The SBS process can become triply resonant when the control field, the Stokes or anti-Stokes field and the acoustic wave are all resonant with the relevant optical and mechanical modes. The triply resonant SBS process, along with the ultrahigh Q-factors and the small mode volume, provides new opportunities for exploring coherent light–acoustic interactions. Over the past few years, low-threshold Brillouin lasers14, Brillouin optomechanics15,16 and Brillouin cooling17,18 have been reported in such triply resonant WGMs.
Here we report the experimental demonstration of Brillouin-scattering-induced transparency (BSIT) and non-reciprocal light storage in a silica microsphere resonator. In contrast to the optomechanically induced transparency that has been observed in a variety of optomechanical systems19,20, two optical modes couple resonantly to an acoustic mode via forward Brillouin scattering in BSIT. A strong optical control field near the lower-frequency optical WGM drives a coherent interaction between the acoustic and the higher-frequency optical WGMs, inducing a transparency window for a probe field near the higher-frequency optical WGM. A number of remarkable coherent optical phenomena and potential applications are possible, such as light storage, dark modes and frequency conversions21,22,23. In addition, due to the phase-matching requirement for travelling waves in SBS, the coherent photon–phonon conversion is only allowed for waves propagating in certain directions. We have taken advantage of this property to demonstrate the non-reciprocal storage and retrieval of a coherent optical field. These results indicate that SBS is an excellent candidate for applications in photonic integrated circuits. With the acoustic vibrations cooled to their motional ground states, applications in a quantum regime, such as single-photon storage and frequency conversion, also become possible24,25,26.
Results
Stimulated Brillouin scattering
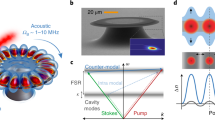
In a silica microsphere resonator, there are optical and acoustic WGMs that propagate along the surface (Fig. 1a). Both optical and acoustic WGMs are characterized by the orbital angular momentum mode number, m. When the acoustic WGM (a) and two optical WGMs (c and d) satisfy the energy and momentum conservations, such that ωa=ωd−ωc and ma=md−mc, photons can be scattered between the two optical resonances through Brillouin scattering15. In this work, we focus on the forward SBS, in which mc and md have the same sign and both optical modes are coupled to travelling waves in the same direction through the tapered fibre, as depicted in Fig. 1a,c. As schematically illustrated in Fig. 1b (more detailes in Supplementary Fig. 1 and Supplementary Note 1), the SBS process, for which the control laser pumps on the lower-frequency optical mode, leads to phonon absorption and anti-Stokes photon generation, whereas the Stokes process is inhibited.
(a) Schematic illustration of the light–acoustic wave interaction in a microsphere. The optical modes of the microsphere are excited by the control and probe lasers through the tapered fibre. These modes interact with the travelling acoustic wave via the forward Brillouin scattering. (b) Spectrum diagram of the coherent photon–phonon interaction: the control laser is near resonance with the lower-frequency mode, and the probe field is on resonance with another cavity mode, whereas the Stokes process is suppressed. (c) The experimental set-up. EOM, electro-optical modulator; FPC, fibre polarization controller. (d) The spectrum of a typical acoustic mode at 42.3 MHz in the microsphere when only the control laser was fixed on resonance with ωc. Inset: simulated deformation of microsphere at the equator for acoustic WGM with ma=6.
Triply resonant SBS was observed for a control laser wavelength near 1,562 nm in a silica microsphere with a radius of 98 μm. We detected the scattered anti-Stokes light by measuring its beating signal with the control laser field. The corresponding power density spectrum was monitored with a spectrum analyser, as shown in Fig. 1d. The Lorentzian lineshape observed indicates an acoustic WGM with a frequency of ωa/2π=42.3 MHz and a linewidth of γa/2π=4 kHz (acoustic Qa≈10,600). The acoustic WGM was also further verified by measuring directly the scattered Stokes light (Supplementary Fig. 2). Using the acoustic velocity in silica, we determined the orbital angular momentum mode number of the acoustic WGM to be ma=6 (inset of Fig. 1d).
Brillouin-scattering-induced transparency
The triply resonant Brillouin scattering discussed above can lead to coherent optical phenomena, such as BSIT, which is an analogue to the well-known electromagnetically induced transparency in atomic system. In a simple and intuitive picture, the control and probe induce a coherent vibration of the acoustic mode. BSIT arises from the destructive interference between the probe field and the anti-Stokes optical field generated by scattering of the control laser from the coherent acoustic vibration. For our system, this destructive interference prevents the excitation of the higher-frequency optical mode. For a detailed theoretical description of BSIT, we consider the system Hamiltonian including the non-linear photon–phonon interaction

where a is Boson operator of the acoustic mode and c,d are Boson operators of the optical modes (see Fig. 1b), g is the single-photon Brillouin coupling rate, which is non-zero only when the phase-matching condition is satisfied. The energy diagram of the system is schematically illustrated in Fig. 2a, where the energy levels are described by phonon and photon Fock states |na, nc, nd›, where na(c,d) is the number of phonons (photons) and Brillouin scattering induces transitions between |na, nc, nd +1› and |na+1, nc+1, nd›. For a strong control laser such as  , the energy diagram can be simplified as Fig. 2b, which has resemblance to the Λ-type system in atomic electromagnetically induced transparency.
, the energy diagram can be simplified as Fig. 2b, which has resemblance to the Λ-type system in atomic electromagnetically induced transparency.
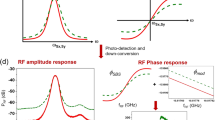
(a–b) Energy diagram for the triply resonant Brillouin scattering discussed in the text. (c–e) Emission power from the higher-frequency optical mode obtained when we scanned the probe frequency by sweeping the modulation frequency Ω of the control laser for several values of control detuning, Δ=1.3,0,−1.3 MHz. Although the peak of the cavity resonance shifts with Δ, the sharp BSIT dip was always observed at δ=0. The incident control power used was 0.3 mW. The insets show the spectral response near δ=0 with an expanded frequency scale. The short-dashed lines are the results of calculations using the parameters kd/2π=3.5 MHz, γa/2π=0.004 MHz and  , 0.05, 0.03 MHz, respectively. (f) The emission power from the higher-frequency optical mode near δ=0 for five different powers of the control beam from 0.18 mW up to 0.35 mW. (g) The spectral linewidth and depth of the BSIT dip as a functions of the cooperativity C, as derived from f. The solid lines in g represent the theoretically expected values.
, 0.05, 0.03 MHz, respectively. (f) The emission power from the higher-frequency optical mode near δ=0 for five different powers of the control beam from 0.18 mW up to 0.35 mW. (g) The spectral linewidth and depth of the BSIT dip as a functions of the cooperativity C, as derived from f. The solid lines in g represent the theoretically expected values.
Under the strong control laser driving, the Hamiltonian is effectively simplified to (see Supplementary Note 2)

where the acoustic mode and the higher-frequency optical mode (mode d) are coupled linearly, with the effective coupling rate determined by the photon number of lower-frequency optical mode. Here, εp denotes the weak probe field with a frequency of ωp coupling to mode d (see Fig. 1b), Δ=ωa+ωl−ωd and δ=ωp−ωl−ωa are relevant frequency detunings, where ωl is the frequency of the control laser. The steady-state intracavity power spectrum is given by,

The intracavity power of mode d is modified by the coherent photon–phonon interaction, giving rise to significant changes in the intracavity power when  is comparable to κd. It is convenient to introduce the cooperativity defined as
is comparable to κd. It is convenient to introduce the cooperativity defined as  , a dimensionless parameter that characterizes the relative strength of the coherent photon–phonon interaction. C also characterizes quantitatively the BSIT process.
, a dimensionless parameter that characterizes the relative strength of the coherent photon–phonon interaction. C also characterizes quantitatively the BSIT process.
To observe BSIT in our system, we probed the intracavity power spectrum in the higher-frequency optical mode using a heterodyne detection technique, with the control laser serving as the local oscillator. We generated the probe field by phase modulating the control laser with an EOM, with modulation frequency Ω. Using a network analyser, the intracavity power can be extracted from the heterodyne signal with modulation frequency Ω. As shown in Fig. 2c–e, we investigated the dependence of the BSIT response on detuning Δ by adjusting ωl with a fixed control power of P=300 μW. The transparency window was observed when the two-photon detuning is near the mechanical resonance frequency, ωp−ωl≈ωa. The lineshapes of the BSIT response, as shown in the expanded spectra in Fig. 2c–e, demonstrate directly the optical interference between the intracavity probe field and the anti-Stokes field. A theoretical calculation of the BSIT response based on equation (3) leads to estimated values of C=5.6, 0.71 and 0.26 for Δ=1.3, 0 and −1.3 MHz, respectively. The triply resonant Brillouin Scattering system enables us to achieve a cooperativity near 6 with a control laser power about 300 μW. Much greater control powers are needed for the achievement of similar cooperativity in WGM-type optomechanical resonantors that do not satisfy the triple resonant conditions.
The strongest cooperativity was not observed at Δ=0, because the triply resonant condition was not exactly satisfied in the experiment, as we estimated ωd−ωc−ωa≈1.3 MHz. Further studies of the BSIT dip at Δ=0 are presented in Fig. 2f, for which the control laser power was varied from 180 to 350 μW. BSIT dips of increasing depths and widths were observed, which can be fitted numerically with a simple Lorentzian lineshape. As shown in equation (3), the linewidth of the BSIT dip is given by (1+C)γa and the relative depth of the BSIT dip is given by  . However, we found that C derived from the numerical fits was not proportional to the input control power because of the thermal effect, which slightly changes the triply resonant condition.
. However, we found that C derived from the numerical fits was not proportional to the input control power because of the thermal effect, which slightly changes the triply resonant condition.
Non-reciprocal light storage
Owing to the coherent Brillouin interaction, the coherent conversion between photons and acoustic phonons can be used for light storage23. In contrast to the previously studied optomechanics driven by radiation pressure and gradient forces, in which the mechanical vibrations can couple to a variety of optical modes, Brillouin scattering is possible only for specific modes that satisfy the energy and momentum conservation conditions. The input control laser coupling to clockwise (CW) optical mode only permits interactions between CW acoustic phonons and photons, whereas the counter-clockwise (CCW) probe field or acoustic wave is decoupled from the control field. Therefore, the requirement of phase matching for the Brillouin scattering process gives rise to the breaking of the relevant reversal symmetry, leading to non-reciprocal non-linear optical processes that are switchable by the control laser.
To demonstrate this non-reciprocity, we studied the light storage of CW or CCW signal fields with a fixed CW control laser. As shown in Fig. 3a, the control and signal fields are switched and frequency shifted by two acousto-optic modulators (AOM 1 and 2), with frequency difference matching ωa. The control laser pulses, including writing and readout, are coupled to the CW mode only. The signal pulse is coupled to either CW or CCW mode by moving a flip mirror. The sequences of writing, readout and signal pulses are shown in the inset of Fig. 3b. When the triply resonant condition is satisfied, the CW signal pulse will be converted to a CW acoustic wave coherently via the beam-splitter-type Brillouin coupling shown in equation (2). The coherence nature of the interconversion between optical and mechanical excitations have been demonstrated in an earlier study of mechanical breathing modes21,27. As shown in Fig. 3b, the CW signal (black line) was stored during the writing pulse and retrieved during the readout pulse after a delay of 3 μs, which is much longer than the cavity photon lifetime. The exponential decay of the signal intensity during the writing pulse results from the underlying dynamical BSIT process. A similar phenomenon has also been reported for mechanical breathing modes in a silica microsphere in ref. 28. The decay time of the converted signal is 14 μs, as determined from an exponential fit (green dashed line in Fig. 3b). In addition, the bandwidth for light storage is determined by the transparency bandwidth of BSIT, (1+C)γa, where C is proportional to the input control power (see Fig. 2f).
(a) The experimental set-up for the non-reciprocal light storage. The CW signal is combined with the CW control laser through a beam splitter (BS2). The CCW signal is launched into the fibre through a circulator. (b) The measured intracavity signal power during the storage and retrieval processes. The black and blue lines correspond to the input signal with different input directions. Inset: the pulse sequences for writing, readout and signal, with the arrows indicating the propagation direction. (c) Schematic diagram of single-bit quantum memory based on circulating acoustic phonons. PBS, polarization beam splitter; PR, polarization rotator.
In comparison, for the CCW-launched signal (blue line), there was no light retrieval during the readout pulse. It should be noted that the flat background signal during the writing pulse originated from the beating between the writing field and the reflected signal field from the end facet of the circulator.
Discussion
In the previous section, we provided experimental evidences of coherent and non-reciprocal photon–phonon interconversion arising from Brillouin scattering in a silica microsphere, though the experiments at room temperature are affected by the thermal acoustic phonons. Since the interaction between the signal field and the acoustic wave with a strong control field is in the form of  (equation (2)), the coherent interconversion should persist even when the signal field is at the single-photon level25. In particular, single-photon storage becomes possible when the relevant acoustic modes are cooled down to their ground states. For ωa/2π=1 GHz and at T=0.5 K, the thermal phonon occupation is near 10. In this case, the ground state cooling requires a cooperativity C >10, which is achievable for silica microspheres, given the reduced thermal bistability and improved mechanical Q factor at the low temperature. Note that the state transfer between a motional state and a microwave field in the quantum regime has already been demonstrated recently in an electromechanical system24.
(equation (2)), the coherent interconversion should persist even when the signal field is at the single-photon level25. In particular, single-photon storage becomes possible when the relevant acoustic modes are cooled down to their ground states. For ωa/2π=1 GHz and at T=0.5 K, the thermal phonon occupation is near 10. In this case, the ground state cooling requires a cooperativity C >10, which is achievable for silica microspheres, given the reduced thermal bistability and improved mechanical Q factor at the low temperature. Note that the state transfer between a motional state and a microwave field in the quantum regime has already been demonstrated recently in an electromechanical system24.
Because of the momentum conservation required for SBS, the degenerate CW and CCW acoustic modes can be written and readout independently by the corresponding CW and CCW control laser. Assuming degenerate CW and CCW optical WGMs in a high-quality whispering gallery microresonator, we can treat a pair of WGMs as one bit of binary information carriers. Here we also proposed a design of quantum memory for polarization-encoded photon state. As illustrated in Fig. 3c, with the use of the polarization beam splitter and the polarization rotator, horizontally and vertically polarized input photon states can individually couple to CW and CCW optical modes. These states can be stored as the CW and CCW acoustic waves and be readout, separately. In principle, the input state, a superposition of polarization state α|H›+β|V›, can be stored as a superposition of circulating acoustic state α|›+β|›. In the reversal of the storage process, the states can be readout by being converted to the photon state α|V›+β|H› after tens of microseconds.
Brillouin scattering in whispering-gallery microresonators is promising in several aspects. (a) Brillouin scattering enables the optical coupling to acoustic waves with frequency ranging from a few MHz to 11 GHz, thereby providing a diverse platform for coherent light-matter interactions. (b) The triply resonant configuration can greatly enhance the Brillouin scattering, thereby reducing the power consumptions15,17. (c) Phase matching for the travelling waves enables non-reciprocal optical processes, thus offering potential application in an all-optical integrated isolator and circulator devices29,30. Our studies pave the way towards the coherent coupling between photons and acoustic phonons and should stimulate further investigations of non-reciprocity and memory at the quantum level.
During the preparation of this manuscript, a similar work has been reported on the arXiv31.
Methods
Experiment method
The experimental set-up is schematically illustrated in Fig. 1c. All experiments were performed at room temperature and at atmospheric pressure. Silica microspheres were fabricated by melting a tapered fibre with a CO2 laser. Optical WGMs in the microsphere were excited through the evanescent field of a tapered optical fibre with a tunable narrow-linewidth (<300 kHz) external-cavity laser at the 1,550-nm band. The coupling strength between the tapered fibre and the optical WGMs can be adjusted by changing the air gap between the fibre and microsphere, which was controlled by a high-resolution translation stage. The optical output was detected using a low-noise photoreceiver, connected to a digital oscilloscope for the measurement of the transmission spectra or to a spectrum analyser for the identification and characterization of the acoustic modes. For the BSIT experiment, an acoustic mode with ωa/2π=42.3 MHz and γa/2π=4 kHz (acoustic Qa≈10,600) was used. The probe field was generated by modulating the control laser through an EOM. A network analyser provided the modulation signal for the EOM and also measured the power spectral density of the beating signal between the control and probe field.
The experiment on optical non-reciprocity was carried out in another silica microsphere with ωa/2π=152.7 MHz and γa/2π=15 kHz (acoustic Qa≈10,180). As shown in Fig. 3a, the control and probe field are generated by two separate acousto-optic modulators (AOM 1 and 2). The writing and readout control pulse sequence was generated by AOM 1, in which a laser beam was frequency shifted by −80 MHz. The signal pulse, which was in synchronization with the writing pulse, was obtained with the use of AOM 2, which frequency shifted the laser beam +72.7 MHz. The peak powers of the writing and readout pulses were both 1 mW, and the peak power of the signal pulse was 20 nW. The durations of writing and reading pulse were 50 and 80 μs, respectively. The two pulses were separated by 3 μs. The forward and backward going signal pulses were separately coupled into the fibre. The power of the optical output was measured with a spectrum analyser operating in a gated-detection mode. The resolution bandwidth was set to 10 MHz.
Additional information
How to cite this article: Dong, C.-H. et al. Brillouin-scattering-induced transparency and non-reciprocal light storage. Nat. Commun. 6:6193 doi: 10.1038/ncomms7193 (2015).
References
Kobyakov, A., Sauer, M. & Chowdhury, D. Stimulated Brillouin scattering in optical fibers. Adv. Opt. Photon. 2, 1 (2009).
Eggleton, B., Poulton, C. & Pant, R. Inducing and harnessing stimulated Brillouin scattering in photonic integrated circuits. Adv. Opt. Photon. 6, 536–587 (2013).
Zhu, Z., Gauthier, D. J. & Boyd, R. W. Stored light in an optical fiber via stimulated Brillouin scattering. Science 318, 1748–1750 (2007).
Okawachi, Y. et al. Tunable all-optical delays via Brillouin slow light in an optical fiber. Phys. Rev. Lett. 94, 153902 (2005).
Pant, R. et al. Photonic-chip-based tunable slow and fast light via stimulated Brillouin scattering. Opt. Lett. 37, 969–971 (2012).
Abedin, K. S. et al. Single-frequency Brillouin distributed feedback fiber laser. Opt. Lett. 37, 605–607 (2012).
Huang, X. & Fan, S. Complete all-optical silica fiber isolator via stimulated Brillouin scattering. J. Lightwave Technol. 29, 2267–2275 (2011).
Poulton, C. G. et al. Design for broadband on-chip isolator using stimulated Brillouin scattering in dispersion-engineered chalcogenide waveguides. Opt. Express 20, 21235–21246 (2012).
Pant, R. et al. On-chip stimulated Brillouin scattering. Opt. Express 19, 8285–8290 (2011).
Shin, H. et al. Tailorable stimulated Brillouin scattering in nanoscale silicon waveguides. Nat. Commun. 4, 1944 (2013).
Rakich, P. T., Reinke, C., Camacho, R., Davids, P. & Wang, Z. Giant enhancement of stimulated Brillouin Scattering in the subwavelength limit. Phys. Rev. X 2, 011008 (2012).
Tomes, M. & Carmon, T. Photonic micro-electromechanical systems vibrating at X-band (11-GHz) rates. Phys. Rev. Lett. 102, 113601 (2009).
Li, J., Lee, H. & Vahala, K. J. Microwave synthesizer using an on-chip Brillouin oscillator. Nat. Commun. 4, 2097 (2013).
Grudinin, I. S., Matsko, A. B. & Maleki, L. Brillouin lasing with a CaF2 whispering gallery mode resonator. Phys. Rev. Lett. 102, 043902 (2009).
Bahl, G., Zehnpfennig, J., Tomes, M. & Carmon, T. Stimulated optomechanical excitation of surface acoustic waves in a microdevice. Nat. Commun. 2, 403 (2011).
Bahl, G. et al. Brillouin cavity optomechanics with microfluidic devices. Nat. Commun. 4, 1994 (2013).
Bahl, G., Tomes, M., Marquardt, F. & Carmon, T. Observation of spontaneous Brillouin cooling. Nat. Phys. 8, 203–207 (2012).
Tomes, M., Marquardt, F., Bahl, G. & Carmon, T. Quantum-mechanical theory of optomechanical Brillouin cooling. Phys. Rev. A 84, 063806 (2011).
Weis, S. et al. Optomechanically induced transparency. Science 330, 1520–1523 (2010).
Safavi-Naeini, H. et al. Electromagnetically induced transparency and slow light with optomechanics. Nature 472, 69–73 (2011).
Dong, C., Fiore, V., Kuzyk, M. C. & Wang, H. Optomechanical dark mode. Science 338, 1609–1613 (2012).
Hill, J. T., Safavi-Naeini, A. H., Chan, J. & Painter, O. Coherent optical wavelength conversion via cavity optomechanics. Nat. Commun. 3, 1196 (2012).
Fiore, V. et al. Storing optical information as a mechanical excitation in a silica optomechanical resonator. Phys. Rev. Lett. 107, 133601 (2011).
Palomaki, T. A., Harlow, J. W., Teufel, J. D., Simmonds, R. W. & Lehnert, K. W. Coherent state transfer between itinerant microwave fields and a mechanical oscillator. Nature 495, 210–214 (2013).
Galland, C., Sangouard, N., Piro, N., Gisin, N. & Kippenberg, T. J. Heralded single-phonon preparation, storage, and readout in cavity optomechanics. Phys. Rev. Lett. 112, 143602 (2014).
Tian, L. & Wang, H. Optical wavelength conversion of quantum states with optomechanics. Phys. Rev. A 82, 053806 (2010).
Qu, K., Dong, C., Wang, H. & Agarwal, G. S. Optomechanica ramsey interferometry. Phys. Rev. A 90, 053809 (2014).
Dong, C., Fiore, V., Kuzyk, M. C. & Wang, H. Transient optomechanically induced transparency in a silica microsphere. Phys. Rev. A 87, 055802 (2013).
Yu, Z. & Fan, S. Complete optical isolation created by indirect interband photonic transitions. Nat. Photonics 3, 91 (2009).
Li, E., Eggleton, B. J., Fang, K. & Fan, S. Photonic Aharonov-Bohm effect in photon-phonon interactions. Nat. Commun. 5, 4225 (2014).
Kim, J., Kuzyk, M., Han, K., Wang, H. & Bahl, G. Non-reciprocal Brillouin scattering induced transparency Preprint at http://arXiv.org/abs/1408.1739 (2014).
Acknowledgements
The work was supported by the National Basic Research Program of China (Grant No.2011CB921200), the Knowledge Innovation Project of Chinese Academy of Sciences (Grant No.60921091), the National Natural Science Foundation of China (Grant No.61308079) and the Fundamental Research Funds for the Central Universities.
Author information
Authors and Affiliations
Contributions
C.-H.D. and Z.S. contribute equally to this work. C.-H.D. and Z.S. prepared the microsphere and carried out the experiment measurements. C.-L.Z., Y.-L.Z. and W.F. provided the theoretical support and analysis. C.-L.Z. and C.-H.D. wrote the manuscript. C.-H.D, C.-L.Z. and G.-C.G. supervised the project. All authors contributed extensively to the work presented in this paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-3, Supplementary Table 1, Supplementary Notes 1-4 (PDF 259 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Dong, CH., Shen, Z., Zou, CL. et al. Brillouin-scattering-induced transparency and non-reciprocal light storage. Nat Commun 6, 6193 (2015). https://doi.org/10.1038/ncomms7193
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms7193
This article is cited by
-
Direct extraction of topological Zak phase with the synthetic dimension
Light: Science & Applications (2023)
-
Long-lifetime coherent storage for microwave photons in the magnomechanical resonator
Quantum Frontiers (2023)
-
Sub-megahertz spectral dip in a resonator-free twisted gain medium
Nature Photonics (2022)
-
Highly efficient acousto-optic modulation using nonsuspended thin-film lithium niobate-chalcogenide hybrid waveguides
Light: Science & Applications (2022)
-
All-fiber optical nonreciprocity based on parity-time-symmetric Fabry-Perot resonators
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.