Abstract
Quantum computation requires a qubit-specific measurement capability to readout the final state of individual qubits. Promising solid-state architectures use external readout electrometers but these can be replaced by a more compact readout element, an in situ gate sensor. Gate-sensing couples the qubit to a resonant circuit via a gate and probes the qubit’s radiofrequency polarizability. Here we investigate the ultimate performance of such a resonant readout scheme and the noise sources that limit its operation. We find a charge sensitivity of 37 μe Hz−1/2, the best value reported for this technique, using the example of a gate sensor strongly coupled to a double quantum dot at the corner states of a silicon nanowire transistor. We discuss the experimental factors limiting gate detection and highlight ways to optimize its sensitivity. In total, resonant gate-based readout has advantages over external electrometers both in terms of reduction of circuit elements as well as absolute charge sensitivity.
Similar content being viewed by others
Introduction
High-fidelity quantum state readout is a requirement for the implementation of a quantum computer. In semiconductor architectures, readout is typically performed via a separate, proximal charge sensor, in contrast to in situ gate-based readout1. To date, the most sensitive electrometers are the radiofrequency quantum point contact (rf-QPC)2,3,4 and the radiofrequency single-electron transistor (rf-SET)5,6,7, providing charge sensitivities at the μe Hz−1/2 level8,9,10. However, the integration of these detectors add additional elements to the architecture, complicating scalability.
Circuit quantum electrodynamics describes an alternative method to readout the state of a quantum system. The self-resonance of a high-frequency resonator is modified by the state-dependent polarizability of the quantum systems coupled to it. It allows readout via the dispersive and dissipative interaction between resonator and qubit. This technique has been demonstrated for superconducting qubits11,12,13,14 and semiconductor charge15,16 and spin qubits17,18. Outside the strong coupling limit of circuit quantum electrodynamics, resonant LC circuits have been coupled directly to the ohmic contacts of double quantum dots to readout their charge and spin state19,20, and to determine their complex admittance21. Furthermore, it has recently been demonstrated that the gates defining these quantum systems can also act as fast and sensitive readout elements, using the state-dependent polarizability as detection mechanism1.
While the high-frequency polarizability of quantum systems is well understood in terms of Sisyphus resistance22, and state-dependent quantum or tunnelling capacitance22,23,24,25, the sensitivity of gate detection has only been reported at the me Hz−1/2 range for GaAs19,26. In other semiconductor materials, charge and spin readout have been achieved27,28,29,30,31,32 and fast detectors have been demonstrated33,34,35 but little progress has been made towards gate-based sensing36. More generally, the noise inherent to any fast-driven two-level system, akin to the cyclostationary noise37 needs to be addressed in order to determine the fundamental limits of charge and phase sensitivity of resonant readout techniques.
In the following, we demonstrate and benchmark a high-sensitivity gate-based charge sensor and calculate the sensitivity limits of resonant readout. The sensor alleviates the need for an external electrometer and simplifies the qubit architecture. It performs at unprecedented levels of sensitivity for gate-based readout, improving on previous semiconductor designs by two orders of magnitude1. The sensor is implemented on the gate electrode of a silicon tri-gate nanowire field-effect transistor (NWFET). By connecting the gate to a radiofrequency resonator we probe the charge state of a few-electron double quantum dot formed at the two top corners of the square NWFET channel. We obtain a charge sensitivity of δq=37 μe Hz−1/2, owing to the strong capacitive coupling between the resonator and the quantum dots (α=Cg/CΣ=0.92, where Cg is the gate and CΣ is the total capacitance, respectively), which could be achieved in any nanowire geometry (for example, InAs or carbon nanotubes). Moreover, we explore the noise sources that limit resonant charge detection in the dispersive and dissipative regime and develop a model of the noise arising from the stochastic nature of electron tunnelling in fast-driven two-level systems. Our calculations show that the sensitivity is limited by a type of noise, which we call Sisyphus noise, that couples to the resonator’s natural frequency of oscillation. We use our model to determine the ultimate charge and phase sensitivity of gate-based detectors and predict that the latter have the potential to outperform rf-SETs.
Results
Device and measurement technique
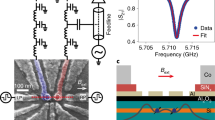
The device used here is a narrow channel silicon-on-insulator (SOI) nanowire transistor. A polycrystalline silicon top gate (length l=64 nm) wraps around three faces of the nanowire and is separated from the channel (width w=30 nm) by an oxide of 1.3 nm equivalent thickness offering a strong control over the channel electrostatics. The electric field exerted by the gate is strongest at the top most corners, where two gate faces meet. Owing to this so-called corner effect, electron accumulation in silicon NWFETs38 happens first at the top most corners. In addition, potential irregularities along the transport direction39,40 confine these corner channels creating a parallel double quantum dot as schematically displayed in Fig. 1a. We couple the double-dot to a resonant LC circuit via the top gate electrode as depicted in Fig. 1b and measure the reflected radiofrequency signal6,19,41. At the resonant frequency ( , CP is the detector’s stray capacitance) the magnitude (γ) and phase (φ) components of the reflected signal are sensitive to admittance changes of the device (Fig. 1c). Changes in the power dissipation in the system are captured in γ, whereas φ reflects susceptance changes because of tunnelling or quantum capacitance1,21,24.
, CP is the detector’s stray capacitance) the magnitude (γ) and phase (φ) components of the reflected signal are sensitive to admittance changes of the device (Fig. 1c). Changes in the power dissipation in the system are captured in γ, whereas φ reflects susceptance changes because of tunnelling or quantum capacitance1,21,24.
(a) Sketch of the cross-section of the device perpendicular to the transport direction. Owing to the corner effect in silicon nanowire FETs and potential irregularities, a parallel few-electron double quantum dot system forms when Vg is biased just below threshold. (b) Electron micrograph of an equivalent device (l=64 nm, w=30 nm) embedded in a resonant tank circuit. Cp is the parasitic capacitance to ground and L a surface mount inductor. Vsd, Vg and Vbg are the DC voltages applied to the source, top gate and back gate, respectively. (c) Characterization of the reflectometry response in magnitude (top frame) and phase (bottom frame) for the OFF (Vg=0 V) and ON (Vg=1 V) state of the transistor. (d) Top panel: energy band diagram as a function of reduced gate voltage ng. The initial detuning position is set by  and δng is the amplitude of the RF excitation. Γ+(−) represents the tunnelling into (out of) the dot. Bottom panel: 3D–0D tunnel rates as a function of ng calculated for EC=15 meV and T=100 mK.
and δng is the amplitude of the RF excitation. Γ+(−) represents the tunnelling into (out of) the dot. Bottom panel: 3D–0D tunnel rates as a function of ng calculated for EC=15 meV and T=100 mK.
The origin of the gate-sensor signal can be understood in terms of electronic transitions in a fast-driven tunnel-coupled two-level system42. Here we consider inelastic charge tunnelling between the quantum dots and the leads. The levels E0 (dot empty) and E1 (dot full) are aligned at ng=0.5 as shown in Fig. 1d. The system is driven cyclically around a DC bias point  with frequency (f0) comparable to the tunnel rate and amplitude
with frequency (f0) comparable to the tunnel rate and amplitude  . Here Cg is the gate capacitance and Vg and
. Here Cg is the gate capacitance and Vg and  are the DC and RF gate voltage, respectively. Starting from the ground state at
are the DC and RF gate voltage, respectively. Starting from the ground state at  , the fast RF excitation δng moves the system out of equilibrium to the right of the degeneracy point. The system is now in the excited state until it inelastically tunnels. The excess dissipated energy ΔE=E0−E1 is then captured as a change in the total reflected power of the device. The dispersive signal may be detected when electrons on average tunnel out-of-phase with the rf cycle, generating an additional tunnelling capacitance contribution Ct=α∂‹ne›/∂Vg, where ‹ne› is the average charge in the island.
, the fast RF excitation δng moves the system out of equilibrium to the right of the degeneracy point. The system is now in the excited state until it inelastically tunnels. The excess dissipated energy ΔE=E0−E1 is then captured as a change in the total reflected power of the device. The dispersive signal may be detected when electrons on average tunnel out-of-phase with the rf cycle, generating an additional tunnelling capacitance contribution Ct=α∂‹ne›/∂Vg, where ‹ne› is the average charge in the island.
The mechanism has previously been studied in the context of Sisyphus dissipation for three-dimensional (3D) metallic islands24,42. Here we transfer the concept to confined systems with a 0D density of states coupled to 3D electron reservoirs. The corresponding tunnel rates are shown in the lower panel of Fig. 1d. A Fermi’s golden rule calculation yields the 3D–0D tunnel rates,

where kB is the Boltzmann constant, T the temperature, ΔE(t)=Ec(1−2ng(t)) the time-dependent energy difference and  is the normalized gate voltage. Γ0 is the constant tunnel rate that establishes away from the degeneracy.
is the normalized gate voltage. Γ0 is the constant tunnel rate that establishes away from the degeneracy.
In order to evaluate the performance of the gate sensor we first compare the results to standard direct current measurements. Fig. 2a shows the characteristic Coulomb diamonds where the electron occupancy is well defined. The onset of current happens at the diagonal lines marked by the green and red arrows indicating the alignment of the electrochemical levels of QD1 to the source and drain reservoirs, respectively (see Fig. 2b). Moreover, we observe a shift of the high-current regions at the orange lines, which can be understood as a capacitive shift of the QD1 transport characteristics because of the loading of an electron on QD2. However, QD2 is only coupled to the source reservoir as depicted in Fig. 2b and cannot be measured in transport.
(a) Source-drain current Isd as a function of Vg and Vsd for Vbg=2.4 V. The numbers (n,m) indicate the electron occupancy in in QD1 (n) and QD2 (m). The coloured arrows point to the onset of the transitions depicted in b. (b) Schematic diagram of a top view of the double-dot configuration. QD1 is tunnel-coupled to the drain (source) indicated by the magenta (green) arrows, while QD2 is only coupled to the source (orange arrow). Gate sensor magnitude response Δγ (c) and phase response Δφ (d) in the same bias region as a. Arrows indicate the same transitions as in a.
The magnitude response of the gate sensor in the same voltage region as the DC transport experiment is presented in Fig. 2c. The signal outlines the edges of the charge-stable regions previously observed in the DC transport measurements. An important difference between the DC and RF measurements is observed, for example, at the QD2 charge transitions (orange arrows). The gate sensor magnitude response is enhanced when the electrochemical levels of dot QD2 and the source reservoir are aligned, demonstrating the possibility to detect charge transitions without the need of current flow or external charge sensors. The detector maintains its sensitivity at high Vsd, as opposed to what is observed in 3D charge islands24. This additional feature stems from the independence of Γ± on Vsd (equation 1).
In Fig. 2d we extract the dispersive contributions by analysing the phase response of the sensor. A change in the effective capacitance of the system because of electron tunnelling modifies the resonator’s resonant frequency and hence causes a phase shift at the sampling frequency (f0). The phase response relates to an effective change in the capacitance, ΔC, of the system given by Δφ≈−πQΔC/CP, where Q is the quality factor of the resonator. Analogously to the magnitude response, we observe this phase shift Δφ at the edges of the conductive regions demonstrating dispersive readout of the charge state of a few-electron quantum dot system. Phase changes of the order of 1 mrad are easily resolved, translating into capacitance detection of ~1 aF, smaller than the ~fF quantum capacitance of strongly coupled quantum systems25.
Experimental charge sensitivity
We now move on to the experimental characterization of the gate sensor’s charge sensitivity. In Fig. 3a we show a typical transfer curve Δγ−Vg of the device comprising two charge transitions. We quantify the sensitivity by applying a small sinusoidal voltage (frequency fs) to the top gate and monitoring the height of the sidebands in the frequency spectrum at f0±fs. We perform this characterization at the point of maximum transconductance of the QD2 transition (red star) since there Γ0 and f0 are well matched. The inset i shows the optimal sideband signal obtained with an equivalent voltage amplitude Δq=0.01e at fs=20 kHz. This results in a signal-to-noise ratio of 15.6 dB and a charge sensitivity of δq=37 μe Hz−1/2 given by  (10), where BSA is the bandwidth of the spectrum analyser used to capture the signal. Owing to the strong capacitive coupling between the radiofrequency resonator and the quantum system (α=0.92), our detector shows an improvement of two orders of magnitude as compared with recent GaAs gate sensors (6.3 me Hz−1/2)1.
(10), where BSA is the bandwidth of the spectrum analyser used to capture the signal. Owing to the strong capacitive coupling between the radiofrequency resonator and the quantum system (α=0.92), our detector shows an improvement of two orders of magnitude as compared with recent GaAs gate sensors (6.3 me Hz−1/2)1.
(a) Typical transfer curve Δγ−Vg showing two electron transitions. Vg=0.5125 V is the first electron on QD1 and Vg=0.5157 V is the first electron on QD2. Inset (i) Sidebands at the point of maximum transconductance (Vg=0.5155 V) at 20 kHz and equivalent excitation amplitude of 0.01 e (solid black line) and fitted curve (dashed orange line). The measurement bandwidth is BSA=1 kHz. Charge sensitivity as a function of carrier frequency (b) and carrier power (c). The 3-dB bandwidth, equivalent to 8 MHz, is indicated by the blue arrow. (d) Top panel: source-drain current (Isd) as a function of source-drain voltage Vsd through a blockaded region at Vg=0.58 V. Bottom panel: noise temperature as a function of source-drain voltage measured at the resonant frequency with a resolution bandwidth of 1 MHz (red solid line). No rf excitation is applied during this measurement. The grey band indicates the calibrated noise temperature of the cryogenic amplifier, TN=7.5±0.2 K. Lossless (e) and lossy (f) impedance matching circuits. Rsis is the Sisyphus resistance of the device, Rs is the inductor equivalent series resistance and Rε is the equivalent dielectric loss of the resonator.
In addition, we study the dependence of δq on carrier frequency and carrier power. Figure 3b shows an optimal δq for a carrier at 335 MHz with a detection bandwidth B of 8 MHz (blue arrow) implying a loaded Q-factor of 42. The optimal excitation power is found to be −85 dBm, which is equivalent to  and a RF amplitude δng=0.03 (Fig. 3c) 50 times larger larger than kBT/EC.
and a RF amplitude δng=0.03 (Fig. 3c) 50 times larger larger than kBT/EC.
Combined with the broad detection bandwidth, the two order of magnitude improvement of sensitivity will now allow single-shot readout of electron spins in semiconductor nanostructures, where T2 times are at least of the order of μs31,43,44. In fact, our gate-based sensor allows submicrosecond detection with an rms charge noise  (ref. 6) of ≃0.1 e. As a whole, these results demonstrate that gate-based readout is a sensitive alternative to the best reported rf-QPCs
(ref. 6) of ≃0.1 e. As a whole, these results demonstrate that gate-based readout is a sensitive alternative to the best reported rf-QPCs  (ref. 9, and normal and superconducting rf-SETs (1 and 0.9 μe Hz−1/2) (refs 8, 10).
(ref. 9, and normal and superconducting rf-SETs (1 and 0.9 μe Hz−1/2) (refs 8, 10).
The sensitivity of rf-SETs is limited by shot noise because of the stochastic nature of the current through the tunnel barriers45. Similarly, resonant readout techniques are in theory limited in their sensitivity by the noise that arises because of the fast drive exerted on the system. A discussion of this type of cyclostationary noise follows in the next section. Here we discuss external factors limiting the gate sensor performance. In Fig. 3d we experimentally characterize the noise temperature of the system at the resonant frequency as a function of Vsd: The top panel shows the source-drain current across a Coulomb blockade region; the bottom panel displays the system’s noise temperature, TN in the same region. TN remains constant independent of the device’s current level and coincides with the noise temperature of the cryogenic amplifier, 7.5±0.2 K highlighted in grey (The amplifier noise was calibrated using shot noise thermometry according to ref. 46.). We conclude that the noise, and hence also the sensitivity of the gated-based charge sensor presented here, is experimentally limited by the noise level of the first amplification stage and is independent of Isd as opposed to shot-noise-limited rf-SET detectors45,47.
Furthermore, degradation of the detector’s sensitivity can arise from external sources of dissipation such as losses in the resonator components. We model these effects using an equivalent lumped-element circuit (see Fig. 3e,f) consisting of the device’s typical Sisyphus resistance (Rsis=300 kΩ), the equivalent series resistance of the inductor (Rs=5.2 Ω) and the equivalent dielectric loss (Rε=16 kΩ) because of losses in the PCB board and the geometrical capacitance of the device (see Supplementary Fig. 1 and Supplementary Note 1). Losses because of the inductor account for a detrimental 10% on sensitivity, which could be improved by the use of a superconducting on-chip inductor. Dielectric losses account for 67% reduction, which could be alleviated by using lower loss PCB boards and optimizing the sample geometry to minimize the parasitic geometrical capacitance. For a lossless circuit as shown in Fig. 3e, we predict that the measured sensitivity could be lowered to 10 μe Hz−1/2.
Finally, an improvement of δq could be achieved if the resonant circuit were designed to match the high Sisyphus impedance of the device, for example, using superconducting transmission lines to make a stub matching network48. We estimate that using this technique a minimum charge sensitivity of 0.9 μe Hz−1/2 could be achieved.
Sisyphus model and comparison to experiment
We now turn to a theoretical description of resonant charge readout. It is substantially different from rf-SETs where the largest contribution to the reflected power comes from the modulation of its differential conductance. In resonant readout schemes single-electron tunnelling is directly coupled to the frequency of the rf-drive and therefore a frequency-dependent noise spectrum is expected. To calculate the fundamental noise that limits resonant charge detection we develop a model of the correlation of the power and phase fluctuations in a fast-driven two-level system. In the following we neglect the back action of photon shot noise since our coupled resonator-qubit system is in the weak-coupling regime49.
We first focus on the dissipative components associated with fast electronic transitions. We present in the following a numerical calculation of the instantaneous dissipated power, P(t), due to the rf excitation, the corresponding spectral density of the fluctuations in dissipated power, Spp, and the charge sensitivity, δq, using experimental parameters obtained earlier.
The dynamics of power dissipation are given by a master equation42. For the 0D–3D tunnel rates (equation (1)) it reduces to solving the differential equation,

where P1 is the probability of the electron being in the dot. Solving equation (2) for P1(t) we obtain the instantaneous dissipated power

as well as its average, ‹P›, over one period  , which is shown in Fig. 4a as a function of DC offset
, which is shown in Fig. 4a as a function of DC offset  . It is displayed for several tunnel rates, using the optimal RF excitation δng=0.03. The most power is dissipated when the system is biased at the charge instability and no dissipation occurs for
. It is displayed for several tunnel rates, using the optimal RF excitation δng=0.03. The most power is dissipated when the system is biased at the charge instability and no dissipation occurs for  , as expected. The change in average power dissipation,
, as expected. The change in average power dissipation,  , is maximum at
, is maximum at  .
.
(a) Calculated average power dissipation as a function of reduced gate voltage  for different tunnel rates Γ0 and reduced rf amplitude δng=0.03. (b) Power spectral density of the power noise, Spp, as a function of normalized frequency f/f0 for several tunnel rates at
for different tunnel rates Γ0 and reduced rf amplitude δng=0.03. (b) Power spectral density of the power noise, Spp, as a function of normalized frequency f/f0 for several tunnel rates at  . (c) Gate-based noise-limited charge sensitivity as a function of tunnel rate (blue line). rf-SET ultimate sensitivity as a function of the ratio between the quantum RQ and tunnel resistance RT (red trace) from ref. 47. RT=2kBT/e2Γ0 at ΔE=0. Inset: zoom-in close to the resonant frequency. The best sensitivity is achieved at the resonant frequency f0. T=100 mK and EC=15 meV throughout the calculations. (d) Experimental (black dots) and simulated data (red solid line, δng=0.0125, T=1 K and Γ0=1 GHz) of the ratio of dissipated power due to the cyclical exchange of electrons ‹P› and total power dissipated by the resonator P0 as a function of Vg. (e) Maximum ‹P›/P0 as a function of tunnel rate Γ0 for the transition indicated by the magenta arrow in Fig. 2c. (Inset) Zoom-in to the region Γ0≈ω0. The red solid line is a fit according to equation 4. Schematic diagrams referring to the no tunnelling (f), inelastic tunnelling (g) and elastic tunnelling regimes (h).
. (c) Gate-based noise-limited charge sensitivity as a function of tunnel rate (blue line). rf-SET ultimate sensitivity as a function of the ratio between the quantum RQ and tunnel resistance RT (red trace) from ref. 47. RT=2kBT/e2Γ0 at ΔE=0. Inset: zoom-in close to the resonant frequency. The best sensitivity is achieved at the resonant frequency f0. T=100 mK and EC=15 meV throughout the calculations. (d) Experimental (black dots) and simulated data (red solid line, δng=0.0125, T=1 K and Γ0=1 GHz) of the ratio of dissipated power due to the cyclical exchange of electrons ‹P› and total power dissipated by the resonator P0 as a function of Vg. (e) Maximum ‹P›/P0 as a function of tunnel rate Γ0 for the transition indicated by the magenta arrow in Fig. 2c. (Inset) Zoom-in to the region Γ0≈ω0. The red solid line is a fit according to equation 4. Schematic diagrams referring to the no tunnelling (f), inelastic tunnelling (g) and elastic tunnelling regimes (h).
With respect to tunnel rates, ‹P› peaks at Γ0=2πf0 showing a way to maximize the detector response. This can be understood from the analytical approximation given in equation (4), where Γ± is expanded around  to the first order of δng.
to the first order of δng.

Note that this approximation is only valid for excitations δng≪kBT/EC. The numerical solution P1(t) of equation (2) (see Supplementary Note 3), furthermore, allows us to calculate the power fluctuations around the mean value and subsequently their power spectral density, Spp (see Supplementary Note 2). The results are shown in Fig. 4b as a function of reduced frequency f/f0 for several Γ0 at  . At the point of maximum sensitivity the power noise is maximum at frequencies that match the excitation frequency f0 and its harmonics. As a whole, these calculations show a new type of frequency-periodic noise, the Sisyphus noise, in which the stochastic nature of electron tunnelling is directly coupled to the resonator’s natural frequency of oscillation. However, signal and noise frequency decoupling could be achieved at the degeneracy point
. At the point of maximum sensitivity the power noise is maximum at frequencies that match the excitation frequency f0 and its harmonics. As a whole, these calculations show a new type of frequency-periodic noise, the Sisyphus noise, in which the stochastic nature of electron tunnelling is directly coupled to the resonator’s natural frequency of oscillation. However, signal and noise frequency decoupling could be achieved at the degeneracy point  (See Supplementary Fig. 2).
(See Supplementary Fig. 2).
Knowledge of the Sisyphus noise and the change in average power dissipation allows us now to calculate the charge sensitivity

in units of e Hz−1/2. The result is presented in Fig. 4c (main panel and inset). In blue we show the charge sensitivity as a function of tunnel rate for Spp(ω)=Spp(2πf0) and  , which corresponds to the experimental situation presented earlier. For our experimental set-up and a range of tunnel rates, the fundamental limit of dissipative rf charge read-out is δq≲70 ne Hz−1/2. As can be seen from the inset of Fig. 4c, the best charge sensitivity occurs for matching tunnel rate and excitation frequency. Adjusting Γ0 and f0 may thus be a route to obtain the best sensitivity, although experimental constraints such as the resonant circuit, that is, f0, will set a practical limit.
, which corresponds to the experimental situation presented earlier. For our experimental set-up and a range of tunnel rates, the fundamental limit of dissipative rf charge read-out is δq≲70 ne Hz−1/2. As can be seen from the inset of Fig. 4c, the best charge sensitivity occurs for matching tunnel rate and excitation frequency. Adjusting Γ0 and f0 may thus be a route to obtain the best sensitivity, although experimental constraints such as the resonant circuit, that is, f0, will set a practical limit.
We benchmark our detector’s ultimate sensitivity against that of rf-SETs predicted in ref. 47 (red trace in Fig. 4c). A direct comparison is made considering the tunnel resistance equivalent RT=2kBT/e2Γ0, which sets the same tunnel rate at ΔE=0 for both cases. Comparing both curves, we find that rf-SETs exhibit a better fundamental charge sensitivity at high tunnel rates, whereas our rf gate sensor performs favourably at low Γ0, that is, for highly resistive tunnel barriers, which is the usual scenario of quantum dots in the few-electron regime.
We confirm the accuracy of our simulations by comparing them to experimental data. In Fig. 4d we plot the ratio of power dissipated in the device, ‹P›, and total dissipated power in the resonator, P0, as a function of Vg across a charge transition point. The lineshape of the peak presents a cosh2 dependence (see equation 4) and is reproduced by our numerical simulations. Furthermore, we compare the experimental and theoretical dependence of ‹P› on tunnel rates. In the cyclical exchange of electrons between dot and electron reservoirs, ‹P› depends on the ratio of the drive frequency ω0=2πf0 and the tunnel rate Γ0, as seen in equation 4. While ω0 is fixed in the experiment, Γ0 can be tuned by changing the profile of the tunnel barriers. This is controlled electrostatically by means of the back gate voltage Vbg. The effect of changing tunnel rates on the detector’s response is demonstrated in Fig. 4e, where we plot the maximum ‹P›/P0 arising from an exchange of electrons between QD1 and the drain reservoir (magenta arrow in Fig. 2c) as a function of Γ0 (see Supplementary Fig. 3). The data are well fitted by our model (red line), and may be understood as follows. At low tunnel rates no additional power is dissipated in the device since there is insufficient time for electrons to tunnel at the rf-drive timescale (Fig. 4f). Equally, at high tunnel rates no power is dissipated as electron tunnelling is elastic (Fig. 4h). However, when Γ0≈0.75ω0, power dissipation is maximized as on average tunnelling happens inelastically at the end of the rf cycle (Fig. 4g). The deviation from the expected Γ0=ω0 at which the dissipated power is maximized (see equation 4) could be a results of a small coupling asymmetry to the source and drain reservoirs of QD1 (see Supplementary Note 4).
Dispersive readout
We now move on to the analysis of dispersive readout and the limits of gate-based phase sensing. Here the change in the probability of the electron being in the dot because of the rf-drive generates a tunnelling capacitance term given by,

which in turn generates a phase shift Δφ(t)∝−Ct(t). We confirm our calculations in Fig. 5a by comparing experimental data to the theoretical average phase shift ‹Δφ›. Similarly to the average power dissipation, the phase response peaks at the degeneracy point and the change  is maximum close to
is maximum close to  . Ct is always positive independently of T and Γ0 and hence ‹Δφ› remains negative, which indicates that on average electron tunnelling leads the rf excitation unless the transient behaviour of the system is probed (see Supplementary Note 2). An analytical solution of equation (6) for δng≪kBT/EC confirms this result,
. Ct is always positive independently of T and Γ0 and hence ‹Δφ› remains negative, which indicates that on average electron tunnelling leads the rf excitation unless the transient behaviour of the system is probed (see Supplementary Note 2). An analytical solution of equation (6) for δng≪kBT/EC confirms this result,
(a) Experimental data (black dots) and simulation (red solid line) of the average phase shift because of the cyclical exchange of electrons ‹ΔΦ› as a function of Vg. The simulation was performed at δng=0.0125, T=1.4 K and Γ0=380 MHz. (b) Power spectral density of the phase noise, Sφφ, as a function of normalized frequency f/f0 for several tunnel rates at  . (c) Noise-limited phase sensitivity as a function of reduced tunnel rate. Lowest phase sensitivity is found for high tunnel rates Γ0>>f0. For all calculations leading to results in b,c T=100 mK and EC=15 meV.
. (c) Noise-limited phase sensitivity as a function of reduced tunnel rate. Lowest phase sensitivity is found for high tunnel rates Γ0>>f0. For all calculations leading to results in b,c T=100 mK and EC=15 meV.

In contrast to the average power dissipation, ‹Δφ› does not peak at the resonant frequency and tends to a constant value for large Γ0. This offers a way to maximize the dispersive signal while reducing the excess power dissipation.
The phase noise spectral density associated with the phase fluctuations is presented in Fig. 5b. It is maximum at multiple of 2f0 with odd harmonics predominantly contributing to the noise spectrum. This can be explained from the time symmetry of the tunnelling capacitance: Ct≈tan(ω0t) is an odd function of time and periodic in 1/2f0 (see Supplementary Note 3). Signal and noise are hence decoupled in frequency space offering an opportunity for high-sensitivity phase detection.
The detector’s ultimate phase sensitivity, δφ, is calculated in the same way as its charge counterpart (see equation (5)) as the ratio of phase noise  and change in average phase
and change in average phase  . It is plotted in Fig. 5c as a function of reduced tunnel rate at bias
. It is plotted in Fig. 5c as a function of reduced tunnel rate at bias  and frequency ω=2πf0. In tune with ‹φ› the phase sensitivity has no minimum at f0 but approaches a low constant value at high tunnel rate. For parameters corresponding to our set-up the fundamental limit of phase sensitivity is δφ≲0.04 μrad Hz−1/2 for tunnel rates Γ0>>f0. Fast gate-based phase detection is thus suitable for systems with transparent tunnel barriers, but performs also well at moderate tunnel rates. This result compares favourably to phase detection based on cooper-pair transistors, which provides sensitivities of the order of 1 μrad Hz−1/2 (ref. 50).
and frequency ω=2πf0. In tune with ‹φ› the phase sensitivity has no minimum at f0 but approaches a low constant value at high tunnel rate. For parameters corresponding to our set-up the fundamental limit of phase sensitivity is δφ≲0.04 μrad Hz−1/2 for tunnel rates Γ0>>f0. Fast gate-based phase detection is thus suitable for systems with transparent tunnel barriers, but performs also well at moderate tunnel rates. This result compares favourably to phase detection based on cooper-pair transistors, which provides sensitivities of the order of 1 μrad Hz−1/2 (ref. 50).
Discussion
In conclusion, we have reported the high-sensitivity resonant charge readout of a few-electron double quantum dot in silicon and studied its experimental and theoretical limits. The ultimate sensitivity of resonant readout, set by the Sisyphus noise arising in fast-driven two-level systems, is comparable to the best rf-SET charge sensors at an equivalent measurement bandwidth. Resonant gate-sensing can be introduced in all semiconductor materials where a strong coupling between gate and qubit can be engineered. A high-sensitivity in situ readout can then be achieved by eliminating sources of excess dissipation such as losses in the inductor and substrate, providing a resonant circuit matching the high-gate impedance, and matching rf-excitation frequency to the electron tunnel rates. Resonant gate-sensing therefore offers a competitive alternative to external charge detectors. The combination of high sensitivity and large bandwidth will allow for single-shot readout of electron spins in semiconductors. Moreover, the flexibility of this technique, which eliminates the need for external sensor elements, opens up a window for high-fidelity, high-integration qubit architectures.
Methods
Device fabrication
The nanowire transistors used in this study were fabricated on SOI substrates with a 145-nm buried oxide. The silicon layer is patterned to create the nanowires by means of optical lithography, followed by a resist trimming process. For the gate stack, 1.9-nm HfSiON capped by 5 nm TiN and 50 nm polycrystalline silicon were deposited, leading to a total equivalent oxide thickness of 1.3 nm. The Si thickness under the HfSiON/TiN gate is 11 nm. After gate etching, a SiN layer (thickness 10 nm) was deposited and etched to form a first spacer on the sidewalls of the gate. 18-nm-thick Si raised source and drain contacts were selectively grown before the source/drain extension implantation and activation annealing. Then a second spacer was formed and followed by source/drain implantations, activation spike anneal and salicidation (NiPtSi).
Measurement set-up
Measurements were performed at the base temperature of a dilution refrigerator. Radiofrequency reflectometry was performed at 335 MHz by embedding the sample in a resonant LC circuit formed by a surface mount inductor (390 nH) and the device’s parasitic capacitance to ground (500 fF). After low temperature and room temperature amplification, the reflected signal was fed into a quadrature demodulator, yielding the signal’s quadrature and in-phase component from which magnitude γ and phase φ are calculated.
Numerical calculations
P1(t) and all subsequent derivatives such as P(t) or Δφ(t) are finite time series in the numerical calculations. P1(t) was obtained by solving equation (2) numerically for a range of parameters corresponding to experimental constraints, namely f0=335 MHz, T=100 mK, EC=15 meV and δng=0.03, at equal time steps in the interval  . The averages ‹P› and ‹Δφ› are taken over one full period. Owing to the finite time series nature of all variables no autocorrelation is necessary, but Spp (Sφφ) can be calculated immediately from the power (phase) fluctuations: SXX(ω)=(Δt)2f0|∑n(X(nΔt)−‹X›) × e−iωn|2.
. The averages ‹P› and ‹Δφ› are taken over one full period. Owing to the finite time series nature of all variables no autocorrelation is necessary, but Spp (Sφφ) can be calculated immediately from the power (phase) fluctuations: SXX(ω)=(Δt)2f0|∑n(X(nΔt)−‹X›) × e−iωn|2.
Additional information
How to cite this article: Gonzalez-Zalba, M. F. et al. Probing the limits of gate-based charge sensing. Nat. Commun. 6:6084 doi: 10.1038/ncomms7084 (2015).
References
Colless, J. I. et al. Dispersive readout of a few-electron double quantum dot with fast rf gate sensors. Phys. Rev. Lett. 110, 046805 (2013).
van Wees, B. J. et al. Quantized conductance of point contacts in a two-dimensional electron gas. Phys. Rev. Lett. 60, 848–850 (1988).
Reilly, D. J., Marcus, C. M., Hanson, M. P. & Gossard, A. C. Fast single-charge sensing with a rf quantum point contact. App. Phys. Lett. 91, 162101 (2007).
Cassidy, M. C. et al. Single shot charge detection using a radio-frequency quantum point contact. App. Phys. Lett. 91, 222104 (2007).
Kastner., M. A. The single-electron transistor. Rev. Mod. Phys. 64, 849–858 (1992).
Schoelkopf, R. J., Wahlgren, P., Kozhevnikov, A. A., Delsing, P. & Prober., D. E. The radio-frequency single-electron transistor (rf-set): a fast and ultrasensitive electrometer. Science 280, 1238–1242 (1998).
Lu, W., Ji, Z., Pfeiffer, L., West, K. W. & Rimberg, A. J. Real-time detection of electron tunnelling in a quantum dot. Nature 423, 422–425 (2003).
Aassime, A., Johansson, G., Wendin, G., Schoelkopf, R. J. & Delsing., P. Radio-frequency single-electron transistor as readout device for qubits: charge sensitivity and backaction. Phys. Rev. Lett. 86, 3376–3379 (2001).
Mason, J. D. et al. A high speed radio-frequency quantum point contact charge detector for time resolved readout applications of spin qubits. Phys. E 42, 813–816 (2010) 18th International Conference on Electron Properties of Two-Dimensional Systems).
Brenning, H., Kafanov, S., Duty, T., Kubatkin, S. & Delsing., P. An ultrasensitive radio-frequency single-electron transistor working up to 4.2 K. J. Appl. Phys. 100, 114321 (2006).
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162 (2004).
Blais, A., Huang, R., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: an architecture for quantum computation. Phys. Rev. A 69, 062320 (2004).
Niemczyk, T. et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat. Phys. 6, 772 (2010).
Barends, R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500 (2014).
Frey, T. et al. Dipole coupling of a double quantum dot to a microwave resonator. Phys. Rev. Lett. 108, 046807 (2012).
Viennot, J. J., Delbecq, M. R., Dartiailh, M. C., Cottet, A. & Kontos, T. Out-of-equilibrium charge dynamics in a hybrid circuit quantum electrodynamics architecture. Phys. Rev. B 89, 165404 (2014).
Petersson, K. D. et al. Circuit quantum electrodynamics with a spin qubit. Nature 490, 380–383 (2012).
Kubo, Y. et al. Strong coupling of a spin ensemble to a superconducting resonator. Phys. Rev. Lett. 105, 140502 (2010).
Petersson, K. D. et al. Charge and spin state readout of a double quantum dot coupled to a resonator. Nano Lett. 10, 2789–2793 (2010).
Schroer, M. D., Jung, M., Petersson, K. D. & Petta, J. R. Radio frequency charge parity meter. Phys. Rev. Lett. 109, 166804 (2012).
Chorley, S. J. et al. Measuring the complex admittance of a carbon nanotube double quantum dot. Phys. Rev. Lett. 108, 036802 (2012).
Persson, F., Wilson, C. M., Sandberg, M. & Delsing, P. Fast readout of a single cooper-pair box using its quantum capacitance. Phys. Rev. B 82, 134533 (2010).
Ashoori, R. C. et al. Single-electron capacitance spectroscopy of discrete quantum levels. Phys. Rev. Lett. 68, 3088–3091 (1992).
Ciccarelli, C. & Ferguson, A. J. Impedance of the single-electron transistor at radio-frequencies. New J. Phys. 13, 093015 (2011).
Lambert, N. J., Edwards, M., Ciccarelli, C. & Ferguson., A. J. A charge parity ammeter. Nano. Lett. 14, 1148–1152 (2014).
Johansson, G., Tornberg, L. & Wilson, C. M. Fast quantum limited readout of a superconducting qubit using a slow oscillator. Phys. Rev. B 74, 100504 (2006).
Maune, B. M. et al. Coherent singlet-triplet oscillations in a silicon-based double quantum dot. Nature 481, 344–347 (2012).
Shi, Z. et al. Fast coherent manipulation of three-electron states in a double quantum dot. Nat. Commun. 5, 3020 (2014).
Morello, A. et al. Single-shot readout of an electron spin in silicon. Nature 467, 687–691 (2010).
Pla, J. J. et al. A single-atom electron spin qubit in silicon. Nature 489, 541–545 (2012).
Pla, J. J. et al. High-fidelity readout and control of a nuclear spin qubit in silicon. Nature 496, 334–338 (2013).
Yin, C. et al. Optical addressing of an individual erbium ion in silicon. Nature 497, 91–94 (2013).
Angus, S. J., Ferguson, A. J., Dzurak, A. S. & Clark., R. G. A silicon radio-frequency single electron transistor. App. Phys. Lett. 92, 112103 (2008).
Manoharan, M., Tsuchiya, Y., Oda, S. & Mizuta, H. Silicon-on-insulator-based radio frequency single-electron transistors operating at temperatures above 4.2 k. Nano. Lett. 8, 4648–4652 (2008).
Nishiguchi, K., Yamaguchi, H., Fujiwara, A., van der Zant, H. S. J. & Steele, G. A. Wide-bandwidth charge sensitivity with a radio-frequency field-effect transistor. App. Phys. Lett. 103, 143102 (2013).
Verduijn, J., Vinet, M. & Rogge, S. Radio-frequency dispersive detection of donor atoms in a field-effect transistor. App. Phys. Lett. 104, 102107 (2014).
Roschier, L. et al. Noise performance of the radio-frequency single-electron transistor. J. App. Phys. 95, 1274–1286 (2004).
Sellier, H. et al. Subthreshold channels at the edges of nanoscale triple-gate silicon transistors. App. Phys. Lett. 90, 073502 (2007).
Betz, A. C. et al. High-frequency characterization of thermionic charge transport in silicon-on-insulator nanowire transistors. App. Phys. Lett. 104, 043106 (2014).
Voisin, B. et al. Few-electron edge-state quantum dots in a silicon nanowire field-effect transistor. Nano Lett. 14, 2094–2098 (2014).
Gonzalez-Zalba, M. F. et al. An exchange-coupled donor molecule in silicon. Nano Lett. 14, 5672–5676 (2014).
Persson, F., Wilson, C. M., Sandberg, M., Johansson, G. & Delsing, P. Excess dissipation in a single-electron box: the Sisyphus resistance. Nano Lett. 10, 953–957 (2010).
Kawakami, E. et al. Electrical control of a long-lived spin qubit in Si/SiGe quantum dot. Nat. Nanotech. 9, 666–670 (2014).
Bluhm, H. et al. Dephasing time of gaas electron-spin qubits coupled to a nuclear bath exceeding 200 μs. Nat. Phys. 7, 109–113 (2011).
Korotkov, A. N. Intrinsic noise of the single-electron transistor. Phys. Rev. B 49, 10381–10392 (1994).
Spietz, L., Lehnert, K. W., Siddiqi, I. & Schoelkopf, R. J. Primary electronic thermometry using the shot noise of a tunnel junction. Science 300, 1929–1932 (2003).
Korotkov, Alexander N. & Paalanen, Mikko A. Charge sensitivity of radio frequency single-electron transistor. App. Phys. Lett. 74, 4052–4054 (1999).
Puebla-Hellmann, G. & Wallraff, A. Realization of gigahertz-frequency impedance matching circuits for nano-scale device. App. Phys. Lett. 101, 053108 (2012).
Schuster, D. I. et al. ac stark shift and dephasing of a superconducting qubit stronly coupled to a cavity field. Phys. Rev. Lett. 94, 123602 (2005).
Roschier, Leif, Sillanpää, Mika & Hakonen, Pertti Quantum capacitive phase detector. Phys. Rev. B 71, 024530 (2005).
Acknowledgements
We thank D.A. Williams for fruitful discussion. The research leading to these results has been supported by the European Community’s seventh Framework under the Grant Agreement No. 318397. The samples presented in this work were designed and fabricated by the TOLOP project partners, http://www.tolop.eu. A.J.F. was supported by a Hitachi Research Fellowship. A.J.F. acknowledges funding from EPSRC under the grant EP/K027018/1.
Author information
Authors and Affiliations
Contributions
A.C.B. and M.F.G.-Z. contributed equally to this work. A.C.B. and M.F.G.-Z. devised and performed the experiments; S.B. fabricated the sample; A.C.B. performed the calculations; M.F.G.-Z. and A.C.B. co-wrote the paper; A.J.F. contributed to the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-3, Supplementary Notes 1-4, Supplementary Methods and Supplementary References. (PDF 2070 kb)
Rights and permissions
About this article
Cite this article
Gonzalez-Zalba, M., Barraud, S., Ferguson, A. et al. Probing the limits of gate-based charge sensing. Nat Commun 6, 6084 (2015). https://doi.org/10.1038/ncomms7084
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms7084
This article is cited by
-
Compilation and scaling strategies for a silicon quantum processor with sparse two-dimensional connectivity
npj Quantum Information (2023)
-
Pulse-controlled qubit in semiconductor double quantum dots
Scientific Reports (2023)
-
Review of performance metrics of spin qubits in gated semiconducting nanostructures
Nature Reviews Physics (2022)
-
Gate reflectometry of single-electron box arrays using calibrated low temperature matching networks
Scientific Reports (2022)
-
Scaling silicon-based quantum computing using CMOS technology
Nature Electronics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.