Abstract
Top predators are a critical part of healthy ecosystems. Yet, these species are often absent from spatially isolated habitats leading to the pervasive view that fragmented ecological communities collapse from the top down. Here we study reef fish from coral reef communities across the Pacific Ocean. Our analysis shows that species richness of reef fish top predators is relatively stable across habitats that vary widely in spatial isolation and total species richness. In contrast, species richness of prey reef fish declines rapidly with increasing isolation. By consequence, species-poor communities from isolated islands have three times as many predator species per prey species as near-shore communities. We develop and test a colonization–extinction model to reveal how larval dispersal patterns shape this ocean-scale gradient in trophic structure.
Similar content being viewed by others
Introduction
Top predators are often conspicuously absent from isolated habitats1,2,3,4,5,6,7,8. Explanations for such spatial variation in trophic structure are numerous: predators often have greater resource requirements9,10,11, larger body sizes12, smaller population sizes13 and slower population growth rates14 than species lower in the food web. Moreover, in some ecosystems, predators are poorer dispersers than their prey, making it less likely that they will colonize isolated habitats, let alone persist there1,15. In marine systems, however, genetic estimates of dispersal distances provide some evidence that species higher in the food web disperse more widely than species in lower trophic levels16. If predators disperse widely, serial influx of colonists could rescue isolated predator populations from extinction. An immediate question, then, is how do differences in the dispersal patterns of predators and their prey affect geographic patterns of community trophic structure?
To answer this question, we analysed a database of published species lists from 35 major coral reef fish communities across the Pacific Ocean consisting of 1,350 total species. Using diet and life history information, we classified each species as either a piscivorous top predator (hereafter predator) or as a species lower on the food chain (hereafter prey). The ratio of the number of predator species to the number of prey species (predator–prey ratio17, R; Fig. 1, circle colour) and total reef fish species richness (circle size) vary widely among Pacific coral reef communities. Total reef fish species richness decreases with increasing isolation as in other systems18,19 and predator–prey ratio varies among islands by a factor of 3 (range: 0.34–1.1 predator species per prey species; Fig. 1). However, in stark contrast to patterns reported from other ecosystems20, the coral reef communities with the highest predator–prey ratios are species-poor communities from the most isolated habitats (for example, Midway, Tuvalu; Fig. 1 inset), whereas communities located near large landmasses (for example, Palau, Vanuatu) have high total species richness and low predator–prey ratios.
Two features of Pacific coral reef communities are at odds with theory and observations from other systems. First, predator–prey ratio is high in isolated communities and low in proximate ones. Second, predator–prey ratio is negatively correlated with total reef fish species richness (Fig. 1, inset) instead of being positively correlated with, or invariant of total richness as in many terrestrial and aquatic ecosystems20. These findings contradict theoretical predictions13,21 and empirical studies of other ecosystems, which suggest that species highest in the food web should be most sensitive to habitat isolation4,10,12,22. Here we develop a mathematical dispersal–colonization–extinction framework that resolves both of these discrepancies. The framework models species composition in a given habitat as an equilibrium between colonization of new species and extinction of those already present23, but builds on this concept by incorporating a basic life history trait of reef fish, the duration of pelagic (open ocean) larval dispersal, which can influence species’ dispersal distances24. We model larval dispersal to predict colonization rate at focal reefs, and use colonization rate to predict how species richness and predator–prey ratio vary across space.
Results
Modelling framework
Most reef fishes exhibit a multi-stage lifecycle involving a dispersive larval stage, followed by a non-dispersive adult stage. The length of time larvae spend in the dispersive stage is known as pelagic larval duration (PLD). Limited dispersal due to limited PLD has been proposed to explain why total reef fish species richness is lower in more isolated habitats and why species that do occur in isolated habitats have higher mean PLD than those inhabiting near-shore habitats18,25. In general, short-term estimates of dispersal distance are positively correlated with PLD among marine species, although the strength of this relationship varies across the range of PLDs26. In this study, we are most interested in dispersal that allows species to colonize new habitats over long ecological timescales (that is, hundreds to thousands of fish generations). Genetic estimates of dispersal distances may provide the best available indices of dispersal distance on such timescales. Genetic estimates of dispersal distance are strongly correlated with PLD, and also agree reasonably well with dispersal distance estimates from computational Lagrangian particle models, which assume that marine larvae disperse like passive particles through the plankton24. Here we take an analytical approach that includes PLD along with other basic features of the larval dispersal process.
To relate PLD to dispersal and colonization rates of predators and prey, we use a diffusion–advection–mortality model27, which describes dispersal of fish larvae from large source populations (Figs 2, 3; full model described in Supplementary Methods). The ratio of predator colonization rate (Cpred) to prey colonization rate (Cprey) at a given location obeys
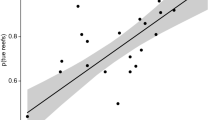
(a) Larval duration data indicate that predators (red) have longer mean PLD than prey (blue; τprey=(28.3, 29.5) days, τpred=38.1 (35.6, 40.7) days, mean number of days (lower, upper s.e.m.); t-test: t=3.92, P<0.001, n prey=347, n predators=35, means and s.e. back-transformed from log scale). (b) Model predicts that predators’ longer larval durations (τpred>τprey) will cause a relatively shallow decay of predator richness (red) compared with relatively rapid decay of prey richness (blue) with increasing habitat isolation. (c) Mechanistic model of predator–prey ratio fitted to data. Model predicts that the predator–prey ratio (R) increases with habitat isolation, measured as squared distance from the focal site to the nearest landmass with area >104 km2 (see Methods for statistics). Predictions are robust to other metrics of isolation.
Larval concentration of a species of predator (red) and prey (blue) at different distances from a source population (dashed vertical white line), given that predator spends more time dispersing than prey. Larval dispersal is modelled using a diffusion–advection–mortality model. Larvae originate at a source location and larval concentration, Ii of prey (i=1) or predators (i=2) is governed by the equation,  , in two dimension (2D; Δ is 2D Laplacian, u and v are mean speeds of advective currents in x and y directions, respectively, σ represents the effective diffusivity of larvae and μi is mortality rate)27.
, in two dimension (2D; Δ is 2D Laplacian, u and v are mean speeds of advective currents in x and y directions, respectively, σ represents the effective diffusivity of larvae and μi is mortality rate)27.

where τpred is predator PLD, τprey is prey PLD, d is the distance between the source of larvae and the focal habitat and σ (σ>0) is the effective diffusivity of predator and prey larvae during dispersal. The ratio of predator larvae to prey larvae colonizing a site will increase with increasing habitat isolation if predators spend more time drifting in the plankton than their prey (that is, τpred>τprey). This is because a longer PLD causes predator larvae to spread farther from their point of release (Fig. 3), creating a distribution of predator larvae that is spread more uniformly over space than the distribution of prey larvae (Supplementary Methods section 4.1 and Supplementary Fig. 2 discuss multiple larval sources). Data from 382 species of Indo–Pacific reef-associated fish from a recently published database28 (Supplementary Data 1; n prey=347, n predators=35) indicate that mean predator PLD is 28% longer than mean prey PLD (Fig. 2a). Equation (1) therefore predicts that the ratio of predator to prey colonization rates should increase with increasing habitat isolation.
To connect colonization rates with standing species richness and predator–prey ratio, we use a colonization–extinction model23 (Fig. 2b,c). In keeping with classical models13, we assume that species within each trophic level colonize and go extinct from habitats identically and independently. We calculate the predator–prey ratio R in a focal habitat as the ratio of the equilibrium number of predator species (Spred) to the equilibrium number of prey species (Sprey),  , where
, where  and
and  are the equilibrium probabilities that any given predator or prey species occur in the community (Supplementary Methods). The dynamics of ppred and pprey can be modelled by the differential equations,
are the equilibrium probabilities that any given predator or prey species occur in the community (Supplementary Methods). The dynamics of ppred and pprey can be modelled by the differential equations,  and
and  , with equilibrium
, with equilibrium  , where the subscript i denotes predators or prey and Ci and Ei denote colonization and extinction rates, respectively13 (we discuss coupling between predators and prey in Supplementary Methods). When the equilibrium occurrence probability of any given species is small,
, where the subscript i denotes predators or prey and Ci and Ei denote colonization and extinction rates, respectively13 (we discuss coupling between predators and prey in Supplementary Methods). When the equilibrium occurrence probability of any given species is small,

Predator–prey ratio is proportional to the ratio of predator to prey colonization rates, which may vary with habitat isolation, and proportional to the ratio of extinction rates, which will not generally depend directly on habitat isolation.
Combining the model of larval dispersal described above (equation (1)) with the equilibrium model for predator–prey ratio (equation (2)) shows how predator–prey ratio depends on habitat isolation:

where r0 and r1 are positive constants that capture factors that do not depend on isolation (for example, differential larval production, differential extinction rates and larval mortality rates). Equation (3) states that predator–prey ratio should increase with increasing isolation distance when predator PLD is longer than prey PLD (that is, τpred>τprey). It also predicts the form of the function relating isolation distance, d, to predator–prey ratio, R. Below we describe how this predicted functional form can be fit to data, and explore whether the model developed above can account for patterns evident in the Pacific reef fish data.
Fitting models to data
By log (ln) transforming both sides of equation (3), we can fit the predicted function of ln(R) as a linear function of d2 directly to the predator–prey ratio data shown in Fig. 1 (fit shown in Fig. 2c, statistical models and spatial autocorrelation discussed in Methods). In what follows, we will refer to d2 as ‘habitat isolation’ and d as ‘isolation distance’. Figure 2c shows that predator–prey ratio increases with increasing habitat isolation as predicted by our model (P=1.8 × 10−4; habitat isolation measured as squared distance to nearest landmass with area >104 km2; other isolation metrics yield similar results; Supplementary Methods). This occurs because predator richness (Fig. 2b, red circles, dashed line) is less sensitive to habitat isolation than is prey richness (Fig. 2b, blue squares, solid line, P=9.5 × 10−6, r2=0.78) as our model predicts, given that predators have longer PLDs than prey (Fig. 2a). The model thus resolves the first discrepancy between observations from other ecosystems and our observations from coral reef communities, that isolated reef communities have the highest predator–prey ratios. Isolated communities have high predator–prey ratios because at their times of settlement, predator larvae are spread more uniformly across space than prey larvae. This makes predator larval supply (Fig. 3), colonization rate and, consequently, species richness (Fig. 2b) relatively insensitive to habitat isolation. Prey richness falls more rapidly with increasing habitat isolation causing predator–prey ratio to rise as isolation increases (Fig. 2c).
A second prediction follows from the form of the functions relating Spred and Sprey to habitat isolation. When currents spread larvae but directional advection is weak, our model predicts that the richness of species in trophic group i is  , where Ki is a trophic level-specific constant (Supplementary Methods). Substituting this expression for prey richness into the corresponding expression for predator richness reveals that
, where Ki is a trophic level-specific constant (Supplementary Methods). Substituting this expression for prey richness into the corresponding expression for predator richness reveals that  ; predator richness should be a power function of prey richness with exponent λ=τprey/τpred. Figure 4 shows this predicted function fitted to the Pacific reef fish data. Communities with higher total richness (that is, points closer to the upper right corner of Fig. 4) are farther from the dashed one-to-one line. As predicted, the relationship between Spred and Sprey is described well by a power function (exponent=0.59, 95% confidence interval (CI)=(0.5, 0.68), P=4.9 × 10−16, r2=0.89); a power function provides better prediction of the data than the linear function that would result if predator–prey ratio were constant (Akaike’s Information Criterion (AIC) power model: 313; AIC linear model: 317), which is consistent with the observation that predator–prey ratio declines as total species richness increases (Fig. 1, inset). Because the power function exponent λ is determined solely by predator and prey PLDs, we can independently estimate λ from the PLD data shown in Fig. 2a. Dividing mean prey PLD by mean predator PLD indicates that λ=0.77 (delta method 95% CI=(0.65, 0.88)), close to the fitted value of 0.59 (0.5, 0.68), particularly considering that the former ignores effects of prevailing directional currents on dispersal patterns. Critically, both predicted and observed exponents are less than 1. The model correctly predicts that communities with low overall richness will have the highest predator–prey ratios, resolving the second discrepancy between patterns of predator–prey ratio in other ecosystems and patterns in Pacific coral reef communities.
; predator richness should be a power function of prey richness with exponent λ=τprey/τpred. Figure 4 shows this predicted function fitted to the Pacific reef fish data. Communities with higher total richness (that is, points closer to the upper right corner of Fig. 4) are farther from the dashed one-to-one line. As predicted, the relationship between Spred and Sprey is described well by a power function (exponent=0.59, 95% confidence interval (CI)=(0.5, 0.68), P=4.9 × 10−16, r2=0.89); a power function provides better prediction of the data than the linear function that would result if predator–prey ratio were constant (Akaike’s Information Criterion (AIC) power model: 313; AIC linear model: 317), which is consistent with the observation that predator–prey ratio declines as total species richness increases (Fig. 1, inset). Because the power function exponent λ is determined solely by predator and prey PLDs, we can independently estimate λ from the PLD data shown in Fig. 2a. Dividing mean prey PLD by mean predator PLD indicates that λ=0.77 (delta method 95% CI=(0.65, 0.88)), close to the fitted value of 0.59 (0.5, 0.68), particularly considering that the former ignores effects of prevailing directional currents on dispersal patterns. Critically, both predicted and observed exponents are less than 1. The model correctly predicts that communities with low overall richness will have the highest predator–prey ratios, resolving the second discrepancy between patterns of predator–prey ratio in other ecosystems and patterns in Pacific coral reef communities.
Discussion
The qualitative predictions of our model are robust to changes in our assumptions about reef fish dispersal and colonization. For example, the simplified model of colonization–extinction dynamics of equation (2) does not account for the dependence of predators on the presence of their prey9,10,11. Incorporating this prey dependence (Supplementary Methods) shows that the predator–prey ratio R can still increase with habitat isolation in a manner consistent with equation (3) for a range of habitat isolation values. The coupled predator–prey colonization–extinction model developed in Supplementary Methods reveals that predator diet specialization also affects the relationship between predator–prey ratio and habitat isolation. If predators are highly specialized, predator–prey ratio will initially increase as habitat isolation increases, but will quickly begin to decline as the prey of specialist predators disappear from isolated habitats, and predators are thereby driven extinct. However, when predators are generalists as in the case of many reef fish predators29, R will continue to increase with habitat isolation over a wide range of isolation values as observed in the Pacific reef fish data. Intuitively, this is because generalist predators can persist on a wide range of different prey and the absence or loss of prey from isolated habitats only affects a predator if all of that predator’s prey species are simultaneously absent. The coupling between predator and prey richness will be even weaker if predators can persist by eating juvenile conspecifics and juveniles of other piscivorous species29. In the extreme case where predators eat juveniles of all species, the coupling between predator and prey equations becomes very weak and the uncoupled equations presented above are approximately recovered (Supplementary Methods).
Processes other than those described by our model undoubtedly contribute to the variation present in Figs 1, 2b,c and 4. We do not consider effects of predators on prey extinction30,31,32, effects of complex trophic structure10, local speciation33, other life history characteristics such as body size, diurnal or nocturnal activity and schooling behaviour28, nor do we consider complex ocean currents34. The amount of population self-recruitment, post-arrival establishment success and species body sizes may differ among predators and prey28, leading to differences in predator and prey extinction rates (equation (2)). However, these differences will not affect the isolation dependence of predator–prey ratio (that is, they affect r1 only in equation (3)) unless they generate a correlation between extinction rate and habitat isolation. Because we are interested in the isolation dependence of the predator–prey ratio, we do not consider these factors explicitly. Previous studies have noted that selective overharvesting of top predators may compound effects of habitat loss on predator richness8. In marine ecosystems, disproportionate fishing pressure on top predators (that is, ‘fishing down food webs’) is well documented35,36,37, although local anthropogenic extinctions are seldom described in reef fish systems. In Supplementary Methods, we explore whether fishing pressure on top predators alone can account for the patterns of reef fish predator–prey ratio described above. Statistical models that contain indices of fishing pressure but lack the functional relationship between predator–prey ratio and habitat isolation derived above provide a poor fit to data. Overfishing of top predators alone does not account for the patterns reported here.
Mounting evidence suggests that species’ dispersal patterns shape community and food web structure in many ecosystems38,39,40,41,42. For example, competing reef fish species in the Great Barrier Reef ecosystem appear to have different dispersal abilities, and this difference may explain the complex patterns of species coexistence observed across the Great Barrier Reef40. Dispersal has also been implicated as a potential cause of geographic variation in the structure of species interactions within local communities (for example, seed dispersal networks on insular versus mainland habitats41). On shorter timescales, it is possible to show experimentally that differences in colonization rates among local habitats cause differences in community structure across a landscape38. For example, invertebrate predators and prey colonize experimental pond habitats at different rates. This differential colonization generates a spatial gradient in the relative abundances of species occupying different positions in a food web38. Variation in colonization rates across a landscape can also create spatial variation in functional structures within local food webs and the rate at which these structures develop during community assembly39,43. The results presented here suggest that effects of dispersal on community trophic structure can extend over a very large spatial scale.
Our study reveals that marine predator species richness is less sensitive than prey richness to habitat isolation, and that this asymmetry causes major variation in trophic structure across Pacific coral reefs. The modelling framework developed here moves from individuals to ecosystems, illustrating how attributes of individual predator and prey larvae influence the dispersal of larval populations, and ultimately create standing variation in predator and prey species richness at an oceanic scale. These results add to a growing body of evidence suggesting that careful consideration of organismal movement may help explain the structure of the ecological communities in ecosystems across the globe. Given the suite of anthropogenic threats facing reef ecosystems44 and top predators more generally45, a renewed focus on the mechanisms that govern community structure is essential.
Methods
Habitat isolation and coastal length
For each of the 35 focal sites, we measured the great circle distance from the centroid of the site to the nearest large potential source of larvae, defined as any landmass >104 km2 (landmass size computed using a global equal area Behrmann projection) that contained coral reef habitat (alternative isolation metrics are discussed in Supplementary Methods). We used coastal length as a measure of habitat size for each focal habitat. Coastal length was computed as the total length of the coastline of each island or set of islands at each of the 35 sites in our database. Lengths of coastlines were measured using SRTM30 PLUS bathymetry (Shuttle Radar Topography Mission) available at http://topex.ucsd.edu/WWW.html/srtm30plus.html.
Species lists and assignment of trophic position
Our data set included species lists from 35 islands/archipelagos with coral reef habitat and included 1,350 shallow-water reef fish species compiled in a recently published reef fish species incidence database46. Seventy-five percent of fish species fell into 23 families that are readily detected during surveys: Gobiidae, Labridae, Pomacentridae, Apogonidae, Serranidae, Muraenidae, Chaetodontidae, Scorpaenidae, Syngnathidae, Ophichthidae, Tripterygiidae, Callionymidae, Carangidae, Pseudochromidae, Lutjanidae, Bothidae, Pomacanthidae, Engraulidae, Soleidae, Ptereleotridae, Monacanthidae, Clupeidae and Lethrinidae. We restricted our analyses to these common families. Including species from all families did not qualitatively change our results. We defined the adult trophic position (that is, predator or prey) of each species using diet, morphology and behaviour information from fishbase ( http://www.fishbase.org) and the primary literature, acknowledging that predation risk in coral reef fishes is high during the early life stage for nearly all species regardless of their trophic position as adults29. Predators were defined as species that consumed fish as ≥50% of their diets as adults. We scored each potential prey species with a palatability score. Palatability 1 is preferred prey (that is, prey that are most heavily targeted by predators); palatability 2 is occasional prey (that is, prey that are not specifically targeted by predators but are eaten occasionally); palatability 3 is rare prey that are seldom targeted by predators; and palatability 4 is non-targeted species that are avoided by predators due to anti-predator traits such as toxins, spines, morphology or behaviour. For the purposes of our analyses, prey were defined as species smaller than 20 cm in total length with palatability scores of 1 or 2. We used this designation because many marine predators are gape limited and avoid consuming heavily armed and otherwise unpalatable species29,47. We also excluded mesopredators that were categorized as both prey and predators. In Supplementary Methods, we explore the sensitivity of our results to the choice of prey designation criteria (that is, palatability and size cut-offs). Our results do not change if alternative criteria are used to define which species are considered prey.
Statistical analysis
As described above, we fitted functions predicted by our theoretical framework to the Pacific reef fish data. For each predicted relationship, we accounted for spatial autocorrelation by using generalized least squares to fit a set of models with different spatial autocorrelation functions. Since we had no a priori expectation about the form of the spatial autocorrelation among sites, we used AIC to compare four commonly used models of spatial autocorrelation: spherical, exponential, Gaussian and rational quadratic. For each analysis, we report statistics from the fit that included the spatial autocorrelation function yielding the lowest AIC value. The linearized model of predator–prey ratio (R) had the form: ln(R)=α1+α2d2+α3ln(coastal length)+Ω, where αj are regression coefficients and Ω includes spatial autocorrelation and normally distributed errors (data and model plotted in Fig. 2c). We included coastal length (a metric of habitat size) as a predictor because habitat size is known to affect species richness, and coastal length varied among the habitats included in our analysis. The Gaussian spatial autocorrelation model had the lowest AIC (AIC=−2.5, r2=0.44). The analysis revealed a significant positive effect of isolation (P=1.8 × 10−4) on log (ln) predator–prey ratio and a significant negative effect of ln coastal length on ln predator–prey ratio (P=4.2 × 10−2).
The linearized model of predator and prey species richness had the same form as the model of predator–prey ratio, but included interactions between predictors and trophic level to allow for the possibility that predator and prey richness were affected differently by isolation and habitat size (Fig. 2b). The linearized model had the form ln(S)=α1+α2d2+α3ln(coastal length)+α4[i]+α5[i × d2]+α6[i × ln(coastal length)]+Ω, where αj are regression coefficients and i is an indicator variable denoting whether each datum was a predator or prey. The statistical fit with Gaussian spatial autocorrelation had the lowest AIC (AIC=5.2, r2=0.78). There was a significant negative effect of isolation on ln richness (P=1.6 × 10−4) and an interaction between trophic level and isolation, such that the ln prey richness-isolation relationship declined more steeply with increasing isolation than the ln predator richness-isolation relationship (P=9.5 × 10−6; Fig. 2b). The effect of ln coastal length on ln richness was also significant (P=7.4 × 10−8), as was the ln coastal length × trophic level interaction (P=3.3 × 10−2), which indicated that ln prey richness increased more rapidly with increasing coastal length than did ln predator richness.
To display data on bivariate plots, we defined habitat size-corrected R=ln(R)−α3ln(coastal length), where α3 is the fitted coastal length dependence of ln(R). For the species richness analysis, we defined habitat size-corrected predator richness=ln(Spred)−α3 ln(coastal length), where α3 is the fitted coastal length dependence for predators, and we defined habitat size-corrected prey richness=ln(Sprey)−(α3+α6)ln(coastal length), where (α3+α6) is the fitted coastal length dependence for prey. All analyses were conducted using the nlme package48 in the R statistical programing language49.
To determine the relationship between the number of predator and prey species at a given site, we modelled the predator richness as a function of prey richness using generalized nonlinear least squares to account for spatial autocorrelation among sites. As predicted, a power function relationship of the form, y=axb provided a good fit to data (Fig. 4). Spatial autocorrelation was best described by a spherical spatial autocorrelation model (AIC=313.3). The power function relationship between prey and predator richness accounted for most of the variation in predator richness (r2=0.89, P=4.9 × 10−16).
Additional information
How to cite this article: Stier, A. C. et al. Larval dispersal drives trophic structure across Pacific coral reefs. Nat. Commun. 5:5575 doi: 10.1038/ncomms6575 (2014).
References
Kruess, A. & Tscharntke, T. Habitat fragmentation, species loss, and biological control. Science 264, 1581–1584 (1994).
Chase, J. M. & Shulman, R. S. Wetland isolation facilitates larval mosquito density through the reduction of predators. Ecol. Entomol. 34, 741–747 (2009).
Didham, R. K., Hammond, P. M., Lawton, J. H., Eggleton, P. & Stork, N. E. Beetle species responses to tropical forest fragmentation. Ecol. Monogr. 68, 295–323 (1998).
Chase, J. M., Bergett, A. A. & Biro, E. G. Habitat isolation moderates the strength of top-down control in experimental pond food webs. Ecology 91, 637–643 (2010).
Laurance, W. F. et al. Ecosystem decay of Amazonian forest fragments: a 22-year investigation. Conserv. Biol. 16, 605–618 (2002).
Terborgh, J. et al. Ecological meltdown in predator-free forest fragments. Science 294, 1923–1926 (2001).
Schoener, T. W. Food webs from the small to the large: the Robert H MacArthur lecture. Ecology 70, 1559–1589 (1989).
Duffy, J. E. Biodiversity loss, trophic skew, and ecosystem functioning. Ecol. Lett. 6, 680–687 (2003).
Holt, R. D., Lawton, J. H., Polis, G. A. & Martinez, N. D. Trophic rank and the species-area relationship. Ecology 80, 1495–1504 (1999).
Gravel, D., Massol, F., Canard, E., Mouillot, D. & Mouquet, N. Trophic theory of island biogeography. Ecol. Lett. 14, 1010–1016 (2011).
Lafferty, K. & Dunne, J. Stochastic ecological network occupancy (SENO) models: a new tool for modeling ecological networks across spatial scales. Theor. Ecol. 3, 123–135 (2010).
Srivastava, D. S., Trzcinski, M. K., Richardson, B. A. & Gilbert, B. Why are predators more sensitive to habitat size than their prey? Insights from bromeliad insect food webs. Am. Nat. 172, 761–771 (2008).
Holt, R. D. inThe Theory of Island Biogeography Revisited eds Losos J. B., Ricklefs R. E. Princeton Univ. Press (2010).
Wilbur, H. M., Tinkle, D. W. & Collins, J. P. Environmental certainty, trophic level, and resource availability in life history evolution. Am. Nat. 108, 805–817 (1974).
Lomolino, M. V. Immigrant selection, predation, and the distributions of Microtus pennsylvanicus and Blarina brevicauda on islands. Am. Nat. 123, 468–483 (1984).
Kinlan, B. P. & Gaines, S. D. Propagule dispersal in marine and terrestrial environments: a community perspective. Ecology 84, 2007–2020 (2003).
Cohen, J. E. Ratio of prey to predators in community food webs. Nature 270, 165–166 (1977).
Mora, C., Chittaro, P. M., Sale, P. F., Kritzer, J. P. & Ludsin, S. A. Patterns and processes in reef fish diversity. Nature 421, 933–936 (2003).
Bellwood, D. R., Hughes, T. P., Connolly, S. R. & Tanner, J. Environmental and geometric constraints on Indo-Pacific coral reef biodiversity. Ecol. Lett. 8, 643–651 (2005).
Warren, P. H. & Gaston, K. J. Predator-prey ratios—a special case of a general pattern. Phil. Trans. R. Soc. Lond. B Biol. Sci. 338, 113–130 (1992).
Nachman, G. Systems analysis of acarine predator-prey interactions. II. The role of spatial processes in system stability. J. Anim. Ecol. 56, 267–281 (1987).
Holyoak, M. & Sharon, P. L. The role of dispersal in predator--prey metapopulation dynamics. J. Anim. Ecol. 65, 640–652 (1996).
MacArthur, R. H. & Wilson, E. O. The Theory of Island Biogeography Princeton Univ. Press (1967).
Siegel, D., Kinlan, B., Gaylord, B. & Gaines, S. Lagrangian descriptions of marine larval dispersion. Mar. Ecol. Prog. Ser. 260, 83–96 (2003).
Hobbs, J.-P. A., Jones, G. P., Munday, P. L., Connolly, S. R. & Srinivasan, M. Biogeography and the structure of coral reef fish communities on isolated islands. J. Biogeogr. 39, 130–139 (2012).
Shanks, A. L. Pelagic larval duration and dispersal distance revisited. Biol. Bull. 216, 373–385 (2009).
Cowen, R. K., Lwiza, K. M. M., Sponaugle, S., Paris, C. B. & Olson, D. B. Connectivity of marine populations: open or closed? Science 287, 857–859 (2000).
Luiz, O. J. et al. Adult and larval traits as determinants of geographic range size among tropical reef fishes. Proc. Natl Acad. Sci. USA 110, 16498–16502 (2013).
Hixon, M. A. inThe Ecology of Fishes on Coral Reefs ed. Sale P. F. Academic Press (1991).
Ryberg, W. A. & Chase, J. M. Predator-dependent species-area relationships. Am. Nat. 170, 636–642 (2007).
Stier, A. C., Hanson, K. M., Holbrook, S. J., Schmitt, R. J. & Brooks, A. J. Predation and landscape characteristics independently affect reef fish community organization. Ecology 95, 1294–1307 (2014).
Stier, A. C., Geange, S. W., Hanson, K. M. & Bolker, B. M. Predator density and timing of arrival affect reef fish community assembly. Ecology 94, 1057–1068 (2013).
Paulay, G. & Meyer, C. Dispersal and divergence across the greatest ocean region: do larvae matter? Integr. Comp. Biol. 46, 269–281 (2006).
Kool, J. T., Paris, C. B., Barber, P. H. & Cowen, R. K. Connectivity and the development of population genetic structure in Indo-West Pacific coral reef communities. Glob. Ecol. Biogeogr. 20, 695–706 (2011).
Pauly, D., Christensen, V., Dalsgaard, J., Froese, R. & Torres, F. J. Fishing down marine food webs. Science 279, 860–863 (1998).
Branch, T. A. et al. The trophic fingerprint of marine fisheries. Nature 468, 431–435 (2010).
Tolimieri, N., Samhouri, J. F., Simon, V., Feist, B. E. & Levin, P. S. Linking the trophic fingerprint of groundfishes to ecosystem structure and function in the California Current. Ecosystems 16, 1216–1229 (2013).
Hein, A. M. & Gillooly, J. F. Predators, prey, and transient states in the assembly of spatially structured communities. Ecology 92, 549–555 (2011).
Fahimipour, A. K. & Hein, A. M. The dynamics of assembling food webs. Ecol. Lett. 17, 606–613 (2014).
Bode, M., Bode, L. & Armsworth, P. R. Different dispersal abilities allow reef fish to coexist. Proc. Natl Acad. Sci. USA 108, 16317–16321 (2011).
Schleuning, M., Böhning-Gaese, K., Dehling, D. M. & Burns, K. C. At a loss for birds: insularity increases asymmetry in seed-dispersal networks. Glob. Ecol. Biogeogr. 23, 385–394 (2014).
Salomon, Y., Connolly, S. R. & Bode, L. Effects of asymmetric dispersal on the coexistence of competing species. Ecol. Lett. 13, 432–441 (2010).
Martinson, H. M., Fagan, W. F. & Denno, R. F. Critical patch sizes for food-web modules. Ecology 93, 1779–1786 (2012).
Pandolfi, J. M. et al. Global trajectories of the long-term decline of coral reef ecosystems. Science 301, 955–958 (2003).
Estes, J. A. et al. Trophic downgrading of planet Earth. Science 333, 301–306 (2011).
Kulbicki, M. et al. Global biogeography of reef fishes: a hierarchical quantitative delineation of regions. PLoS ONE 8, e81847 (2013).
Gill, A. The dynamics of prey choice in fish: the importance of prey size and satiation. J. Fish Biol. 63, 105–116 (2003).
Pinheiro, J., Bates, D., DebRoy, S. & Sarkar, D. Linear and nonlinear mixed effects models. R Package Version 3.1-117, 57 (2014).
R Development Core Team. R: a Language and Environment for Statistical Computing R 3.0 ednR Foundation for Statistical Computing (2013).
Acknowledgements
The paper benefitted from discussion with C. Osenberg, M. McCoy, B. Bolker, M. O’Connor, K. Lafferty, S. McKinley, J. Samhouri, O. Shelton, R. Fletcher, T. Palmer and R. Holt and from R. Becheler’s contribution to the PLD database. This work was supported by the Ocean Bridges program funded by the French American Cultural Exchange, GASPAR and RESICOD programs from Fondation pour la Recherche en Biodiversité, the National Science Foundation (Grant No. DGE-0802270 to A.M.H. and Grant No. 0801544 in the Quantitative Spatial Ecology, Evolution and Environment Program at the University of Florida), a Killam Postdoctoral Fellowship to A.C.S. at University of British Columbia and the support of the Gordon and Betty Moore Foundation to the Ocean Tipping Points project.
Author information
Authors and Affiliations
Contributions
A.C.S., A.M.H. and M.K. designed the study and wrote the manuscript. V.P. gathered geospatial data. A.M.H. performed statistical and mathematical analyses and V.P. and M.K. contributed the database of fish biodiversity and larval durations in the South Pacific.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Figures, Table, Methods, and References
Supplementary Figures 1-3, Supplementary Table 1, Supplementary Methods and Supplementary References (PDF 966 kb)
Supplementary Dataset 1
Larval durations for each of the Indo-Pacific predator and prey species considered in this study (DOCX 288 kb)
Rights and permissions
About this article
Cite this article
Stier, A., Hein, A., Parravicini, V. et al. Larval dispersal drives trophic structure across Pacific coral reefs. Nat Commun 5, 5575 (2014). https://doi.org/10.1038/ncomms6575
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms6575
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.