Abstract
The energetics of metal/molecular semiconductor interfaces plays a fundamental role in organic electronics, determining the performance of very diverse devices. So far, information about the energy level alignment has been most commonly gained by spectroscopy techniques that typically require experimental conditions far from the real device operation. Here we demonstrate that a simple three-terminal device allows the acquisition of spectroscopic information about the metal/molecule energy alignment in real operative condition. As a proof of principle, we employ the proposed device to measure the energy barrier height between different clean metals and C60 molecules and we recover typical results from photoemission spectroscopy. The device is designed to inject a hot electron current directly into the molecular level devoted to charge transport, disentangling the contributions of both the interface and the bulk to the device total resistance, with important implications for spintronics and low-temperature physics.
Similar content being viewed by others
Introduction
The energetics of metal/molecule interfaces has been the subject of intensive study over the past two decades1,2. Significant energy barriers build up between the metal Fermi energy and the molecular levels devoted to charge transport, limiting the charge injection from the metals to the molecular semiconductors. These energy barriers have a deep impact on the performances of devices, determining the operation voltage in organic light emitting diodes3, the threshold voltage of field-effect transistors4 and the open circuit voltages in photovoltaic devices5. Therefore, an accurate knowledge of the energetics is necessary for the engineering of metal–molecule interfaces and the consequent optimization of the device performances. Different approaches have been applied to the study of metal/molecule interfaces, such as electron photoemission spectroscopy1,2 and Kelvin probe measurements6. In such experiments the energy level alignment is typically extracted by monitoring the change in the work function when thin molecular layers are evaporated on to the surface of a metal. Therefore, it is not possible to monitor directly how the measured energy level alignment reflects on to the electrical charge injection. In this sense, it is of major interest to gain the same spectroscopic information from direct electrical measurements in a device. As the energy level alignment determines the charge injection, it ultimately lies hidden in the current–voltage characteristics of metal/molecular semiconductor/metal stacks. However, by performing direct current (I)–voltage (V) measurements, it is generally difficult to discern between two different contributions to the device resistance: the contact resistance (connected to the interfacial energy barrier) and the resistance of the bulk semiconductor1.
In this communication we demonstrate precise measurement of the barrier for charge injection in a device in which the contribution of the contact and the bulk resistance are well separated. As a proof of principle, we focus on the interfaces between C60 and different metals. Several reports show that significant charge transfer takes place at such interfaces, resulting in strong interfacial dipoles and band bending7,8,9,10,11,12,13. Here we directly measure the metal/C60 energy barriers for carrier injection in a vertical device geometry, and study how these barriers determine the in-device electrical resistance. Furthermore, our approach allows the injection of carriers into molecular semiconductors above the energy barrier, thus free from the contact resistance, with interesting implications for spintronics and low-temperature physics.
Results
Device scheme and fabrication
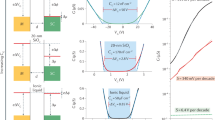
Our device is based on ballistic electron emission14,15. This principle has been first applied in microscopy, where a scanning tunnelling microscope tip is used to inject a hot electron current into a thin metal layer deposited on to a semiconductor. An analysis of the current flowing through the semiconductor allows one to obtain information on the interfacial energy barrier. This technique was first applied to the study of the energy barrier at metal/inorganic semiconductor interface14,15, and only recently it has been applied to metal/molecule systems16,17. Here we perform ballistic electron emission spectroscopy in a solid-state device by replacing the electron injection from the scanning tunnelling microscope tip with a large-area tunnel barrier. More specifically, our device is composed of an emitter, a base and a collector (as shown in Fig. 1a,b). The emitter and the base are two metallic electrodes separated by a tunnel junction. The emitter is a 13-nm-thick Al contact that is plasma-oxidized in situ to create a thin AlOx barrier. As a base we employ different metals for the determination of the energy level alignment between them and the adjacent C60 molecules. A 200-nm-thick C60 layer serves as a semiconducting collector. A 15-nm-thick Al top electrode is used for the actual electrical contact to C60. The energy alignment between the Fermi level of emitter and base is externally controlled with the external bias VEB (see Fig. 1a), while the energy alignment at the base/collector interface is naturally given by the metal/C60 energy barrier Δ.
This working principle is used to measure the energy barrier at metal/C60 interfaces. (a,b) Scheme of the energetics of the device. EF represents the Fermi energy of the metals. The tunnelling current IE flows when a bias VEB is applied at the emitter/base terminals. When the bias VEB is lower than the energy barrier Δ at the metal/C60 interface, IE flows into the base where it is measured as base current IB. In this case, no current is measured into the C60 (a). When the bias VEB is higher than Δ, part of the tunnelling current IE flows into the C60 and is measured as collector current IC-hot even in the absence of an external voltage directly applied across C60 (VBC=0) (b). (c) Hot electron current IC-hot as a function of the applied bias between emitter and base VEB measured at the collector in a device with a 10-nm-thick Cu base at 245 K. The barrier height is Δ=0.95 V, as obtained by interpolating the linear fit of the growth and the I=0 line.
When the bias VEB is applied, a current IE is injected from the emitter into the device as electrons tunnel through the AlOx barrier. These injected electrons are regarded as ‘hot’ in the base, because their energy level is well above the Fermi energy level of the metal base. A fraction of these electrons go through the base ballistically with no energy attenuation, provided that the base is sufficiently thin (in a few nanometre range). If the external voltage VEB is lower than the barrier Δ, these ballistic electrons are reflected at the metal/C60 interface and flow as the base current IB. In this case, all the emitted current IE flows in the base terminal (IE=IB) and no collector current is measured (IC=0, Fig. 1a). Instead, if VEB>Δ, then some of the hot electrons enter the C60 layer and diffuse towards the top Al electrode, where they are collected as IC. Since IC generates from the hot electrons in the base, we refer to it as IC-hot. In this case, a part of the emitted current flows into the base and the other part into the collector (IE=IB+IC-hot, Fig. 1b). The information about the energy barrier lies in IC-hot(VEB), since it is IC-hot=0 for VEB<Δ and IC-hot≠0 for VEB>Δ (ref. 14). A typical measurement of IC-hot versus VEB is shown in Fig. 1c for a device with a 10-nm-thick Cu metal base. Clearly, IC-hot=0 is fulfilled when VEB is below a certain threshold, and then increases roughly linearly15. To obtain the barrier height, we employ a simple and visual method as shown in Fig. 1c. We fit the rise of IC-hot above VEB by a linear function over some hundreds of mV and we use the voltage at which the fitting line intercepts I=0 as an approximation of the barrier height. In the case of Fig. 1c, we obtain Δ=0.93 V.
We highlight that since C60 is an n-type semiconductor, we measure the energy barrier between the Fermi level of the metal base and the lowest unoccupied molecular orbital (LUMO) of C60, which is the orbital devoted to the charge transport. This also implies that if the base is kept at ground potential (Fig. 1a,b), VEB must be negative to inject hot electrons into the base and then into the C60 layer. Moreover, the current IC-hot is measured without external VBC applied across the C60 terminals; thus IC-hot can be regarded as a purely diffusive current steaming exclusively from the emitter. Two factors make possible the current flow into the C60 layer without any externally applied bias. First, the electrons that are injected into the C60 layer possess a component of the momentum directed perpendicular to the metal/C60 interface14,15, with which they diffuse towards the top electrode. Second, inside the C60 layer there is an internal electric field due to the difference between the work function of the two metals sandwiching the C60 layer18. Since the top Al electrode has the highest work function between all metals of this study (see below), the electric field is always directed to accelerate the electrons towards it. For trap-free inorganic semiconductors, analogous factors—the initial velocity and the acceleration of the electric field present at the metal/semiconductor Schottky barrier—are sufficient for the electrons to diffuse and be collected as current. For this reason, the analysis of the wide majority of the ballistic electron emission experiments based on inorganic semiconductor does not take into account the bulk resistance of the collector14,15,19,20,21. The electrons allowed to enter into the collector thermalize quickly in the semiconductor21, but they are considered free to diffuse into the semiconductor, where they are collected as hot electron current. This assumption is justified in inorganic band-like semiconductors, where the extremely low-defect concentration allows an almost ideal trap-free transport. Indeed, only at very low temperatures (below 10 K) the resistance of inorganic semiconductors was found to play a role in the determination of the magnitude of IC-hot (ref. 22). For C60, the assumption of trap-free transport is not justified, and we found that the bulk resistance of C60 has a strong impact on the magnitude of the current IC-hot, as shown in the next section.
Electrical characterization
When the base material is ferromagnetic, the hot electron current injected in the semiconductor possesses a very high spin polarization21, with interesting implications for spintronics23. For this reason, throughout this article we mainly focus on the electrical characterization of devices based on a ferromagnetic Ni80Fe20 (NiFe) base. Figure 2 shows the typical electrical characterization of a device with a 7-nm-thick NiFe base at three different temperatures. The I–V characteristics of the tunnel junctions are shown in Fig. 2a. The resistance slightly increases when lowering the temperature, as expected for continuous tunnel junctions. Figure 2b shows the IBC-2t–VBC characteristics of NiFe/C60/Al stack. In this case the current flowing in the C60 is driven by a sweep of the voltage VBC directly at the NiFe/C60/Al electrodes, so it is a conventional two-terminal measurement comprising the contribution of the contact and the bulk resistance. To avoid confusion with IC-hot, we refer to this as IBC-2t. The temperature evolution of the IBC-2t–VBC traces shows the thermally activated behaviour typical of transport through thick-layer molecular semiconductor24. At every temperature, the IBC-2t–VBC characteristics show a diode-like shape. More current flows into the device when electrons are injected by the top Al layer (VBC<0), while the current injected by the NiFe electrode (VBC>0) is extremely low below 1 V, suggesting the formation of a high energy barrier at the NiFe/C60 interface.
(a) Current IE measured at two terminals in the Al/AlOx/NiFe tunnel junction as a function of the applied bias. (b) Current IBC-2t measured at two terminals in the NiFe/C60/Al stack as a function of the applied bias. Negative and positive polarity correspond to electron injection by the top Al and the bottom NiFe electrodes, respectively. (c) Hot electron current IC-hot measured in the NiFe/C60/Al stack as a function of the applied bias between emitter and base. The barrier height Δ is obtained by interpolating the linear fit of the growth to I=0. (d) Temperature dependence of IC-hot measured at VEB=−1.5 V and VBC=0.
Figure 2c shows the IC-hot–VEB characteristics of the device at the same temperatures. Interestingly, the temperature dependence of IC-hot and IBC-2t are very different.
In Fig. 2c, we observe that IC-hot at 210 K is higher than that at 240 K, even though IBC-2t of the NiFe/C60/Al stack at 210 K is one order of magnitude lower than that at 240 K. This result is explained by the fact that the two-terminal measurement of Fig. 2b is a sum of the contribution of the interface resistance plus the bulk resistance. For a device with a 200-nm-thick molecular layer, the resistance is interface dominated24 and the current decrease is due to the unfavourable carrier injection.
Instead, the current IC-hot flowing in Fig. 2c is not affected by the interface resistance since the electrons are injected above the energy barrier. IC-hot increases because in this temperature range electrons undergo less scattering with phonons in the base, so more electrons are allowed to travel ballistically and reach the collector20.
The variation of the current IC-hot measured at VEB=−1.5 V in a device with a NiFe base is shown in Fig. 2d. Below 210 K, IC-hot begins to drop as a result of the decreasing mobility of the C60 film. As in ordinary molecular semiconductors, the mobility of C60 becomes very low with decreasing temperature25, so that the injected electrons cannot diffuse through the whole C60 film. Instead, they get trapped into shallow traps of the molecular layer, effectively causing the decrease in IC-hot. In this respect, while the ‘onset’ of IC-hot is related to the barrier height, its ‘magnitude’ is related to the electron transport through the bulk C60 layer. The one-order-of-magnitude decrease in IC-hot between 240 and 10 K is very limited when compared with the variation in IBC-2t, which decreases five orders of magnitude in the same temperature range (the current IBC-2t at 10 K is shown below). Thus, the temperature dependence of the current is a good criterion to confirm the ‘hot electron’ origin of the current IC-hot.
An analogous temperature dependence was observed in silicon at much lower temperatures, with the hot electron current decreasing below 10 K22. Compared with Si (ref. 22), the current in C60 starts to decrease at much higher temperature. This result is due to the higher numbers of traps of our disordered C60 layer as compared with Si and it is expected on the basis of the different transport mechanisms in the two materials. In a similar device based on Alq3, the hot electron current could not be measured without externally applied bias since the mobility of Alq3 is too low to allow electrons to diffuse through it even at room temperature26. In that case, the electrical characteristics of the device were explained by considering that all the injected electrons would get trapped into the first molecular layer.
Effect of the external bias voltage VBC
The current IC-hot injected into the C60 layer at 10 K is shown in Fig. 3a. Following the discussion above, the magnitude of IC-hot is lower at 10 K than at 210 K (compare Figs 2c and 3a). However, IC-hot can be increased by applying an external bias at the base–collector directed as to accelerate the hot electrons towards the Al collector. As shown in Fig. 3b, when an external bias voltage VBC=3 V is applied the magnitude of IC-hot reaches 300 nA, two orders of magnitude higher than for the case VBC=0. Such an increase can be explained considering that an electric field is capable of removing electrons from shallow traps27 so that more electrons can contribute to IC-hot.
Current IC-hot as a function of the applied bias between emitter and base VEB measured at 10 K for the same device with different applied bias across the C60 film: (a) VBC=0 and (b) VBC=3 V. (c) The two-terminal current IBC-2t as a function of the bias VBC applied across the C60 at the same temperature.
We note that at 10 K the two-terminal resistance of C60 is extremely high, as shown in Fig. 3c. In particular, the current flowing into C60 driven by the external voltage VBC=3 V is well below 1 nA. Therefore, the current introduced by the direct voltage VBC would not explain the increase in IC-hot. This same experiment could not be performed at temperatures above 200 K, since in that case the current introduced by directly biasing the C60 film would be higher than the increase in the current IC-hot. We mention that at 10 K it would not be possible to inject a 300-nA current by directly biasing the C60 layer since one should apply a bias voltage higher than the breakdown voltage of the layer (which was found to be below 6 V). For this reason, we believe that this method could be employed to obtain sizable current intensity flowing in semiconductors at very low temperatures, in a range where the contact resistance usually prevents an efficient carrier injection.
Energy barriers at different metal/C60 interfaces
A direct comparison of the measurements of the energy barrier for different base materials (Au, Cu, and NiFe) is shown in Fig. 4. The work functions of these materials are shown in Fig. 4a compared with the energy levels of C60 and with the work function of Al, which is used as top electrode in the C60 collector. Al has the lowest work function, which is quite well matched with the LUMO of C60. All the other metals have a work function between the highest occupied molecular orbital (HOMO) and the LUMO. The IBC-2t–VBC traces of all the metal/C60/Al present a diode-like I–V characteristic similar to those shown in Fig. 2b for the NiFe base (Supplementary Fig. 1).
(a) Comparison between the work functions ϕ of the different materials used in this study and the molecular levels of C60. The values are taken from ref. 1,2. (b) Hot electron current IC-hot as a function of the applied bias between emitter and base VEB measured in devices with different metal bases: Au, Cu and NiFe. The measurements are carried out at 210 K. The barrier height Δ is obtained by interpolating the linear fit of the growth to I=0.
In Fig. 4b we show the IC-hot–VEB characteristics measured in the devices with the different metal bases. The thickness of the three bases was chosen to be different to account for the different attenuation length in the different metals. In particular, the energy attenuation length is shorter in ferromagnetic metals, so that we employed a 7-nm-thick NiFe base and 10-nm-thick Cu and Au bases to measure comparable currents. Indeed, the order of magnitude of the currents is the same in the three cases described in Fig. 4. By contrast, we find that the voltage dependence of the IC-hot turns out to be different. In particular, the slope of the line fitting the experimental data for VEB<Δ is different in the three cases. This is explained as follows. The current reaching the top Al electrode is a fraction of the current flowing into the tunnel junction. Therefore, higher current flowing into the tunnel junction corresponds to higher current getting to the top Al electrode. In the case of Fig. 4b, the resistance of the tunnel junction based on NiFe and Cu are comparable, while the resistance of the Au tunnel junction is one order of magnitude higher (Supplementary Fig. 2), explaining why the increase of IC-hot in the Au device is less steep than the increase in the other two devices. Furthermore, although the C60 layer was grown always at the same substrate temperature and at the same deposition rate, its transport properties were reproducible only within one order of magnitude, thus introducing some variability on the shape of the IC-hot–VEB trace.
Separation of contact and bulk resistance
We show now that the device allows distinguishing between the contribution of the interface and of the bulk to the total resistance of C60. To do so we measure a device before and after annealing (performed at 10−6 mbar and 200 °C for 1 h). Again, we focus on a device with a NiFe base.
Figure 5a shows the current IBC-2t as a function of VBC at 150 K before (red) and after (blue) annealing. Clearly, the two-terminal resistance of the NiFe/C60/Al stack decreases during the annealing step: before annealing the current IBC-2t at 150 K is extremely low (below the detection limit between −1 V and 1 V), while a significant current amount of flows at the same temperature after the annealing. By considering only the data in Fig. 5a, it would be difficult to understand whether the conductivity change is connected to a modification of the injection barrier or rather to a change in the conductivity of the bulk C60. In fact, an interpretation based on a modified barrier was put forward to explain the increase in conductivity measured in a similar structure28. In the present case, we could directly measure the barrier height before and after the annealing. Figure 5b shows IC-hot versus VEB before and after the annealing. In both cases, we obtain the barrier height Δ=1.21 V. Thus, the change in the two-point conductivity of the NiFe/C60/Al stack is not related to a change in the barrier height, so that it must be due to an improved conductance through the bulk C60. Indeed, the annealing improves the ordering of the molecular layer and thus its mobility. Furthermore, we notice that after annealing also the magnitude of the current IC-hot increases. As discussed above, we relate such an increase to the improved conductance of the bulk C60.
(a) Current IBC-2t measured at two terminals in the NiFe/C60/Al stack as a function of the applied bias VBC at 150 K for the same device before and after an annealing process. (b) Hot electron current IC-hot as a function of the applied bias between emitter and base VEB measured at 150 K for the same device before and after the annealing. In both I–V traces a voltage VBC=1 V is applied during the measurement to increase the measured hot electron current.
Discussion
The energy level alignment is ultimately determined by the electric dipoles that build up at the metal/molecule interfaces1,2. A ubiquitous contribution to the interface dipole at metal/organic interfaces arises from a rearrangement of the metal electron density on the deposition of the organic layer. At the metal surface, the tail of the electronic density protruding into vacuum is reduced because of the Coulomb repulsion with the molecules. This effect, called push-back or pillow effect, has been reported in different metal/organic surfaces29,30,31 and contributes to explain the results of our metal/C60 interfaces.
On the other hand, the energy barrier at the NiFe/C60 interfaces (Δ=1.2 V) is substantially higher than the energy barriers at Au/C60 (Δ=0.89 V) and Cu/C60 (Δ=0.93 V). This result would not be expected on the basis of just the different work functions of the various metals. In particular, Au has the highest work function, so one would expect it to form the highest barrier for electron injection with C60. Instead, we find that its barrier is the lowest. This result shows that the work function is not the only important factor for the determination of the interfacial energetics. In fact, in addition to the push-back effect, the amount of transferred charge depends on the material hardness, defined as the derivative of the chemical potential with respect to the number of electrons32. The hardness is an indication of the ease of a metal to transfer charge, and it is inversely proportional to the density of states at the Fermi level. Au and Cu have density of state at the Fermi level lower than NiFe, so that they are harder, that is, less prone to donate charge29. The interfacial dipoles are expected to be lower than those which build up at the NiFe/C60 molecule interfaces, nicely explaining the measured differences in energy barriers. Our results are in agreement with spectroscopy data, showing highest hybridization at the C60/Ni interface as compared with Au and Cu (refs 10, 11).
Furthermore, additional information can be extracted by studying the shape of the increase of IC-hot close to the energy barrier. From Fig. 4b, it is known that the IC-hot–VEB for NiFe is far from the linear fitting we employ to extract the barrier height. This effect can be explained taking into account the density of states of the molecular semiconductor. At the interface, the molecular levels broaden because of the interaction with the metal surface, with a broadening that can be approximated by a Gaussian or a Lorentzian distribution1,2,24. Therefore, the electrons can enter into the semiconductor before reaching the LUMO since they find available states in the tail of the LUMO energy broadening, as schematically shown in Supplementary Fig. 3a. The energy broadening of the LUMO of the C60 is expected to be quite different in the three cases since it depends on the degree of interaction between the molecules and the metal surface.1,24 Therefore, since NiFe is the metal that interacts the most, the NiFe/C60 has not only the highest energy barrier, but also the highest energy broadening. In this regard, we believe that the shape of the current increase at the cut-off returns information on the shape of the density of states in the molecular film. In Supplementary Note 1 we develop a detailed model that takes into account the density of states of the molecular semiconductor to fit the data of Fig. 4. By employing such model, we can closely reproduce the shape of the curves as shown in Supplementary Fig. 3.
Finally, we discuss how this device scheme can be further extended to other experimental situations. From a technical point of view, the device production and measurement does not present particular complications and can be readily reproduced. Basically, the structure of our device is nothing but a metal/semiconductor/metal stack grown on an Al/AlOx contact, which serves as electron injector. The Al/AlOx contact is in turn easy to produce since Al is widely used in organic electronics and the AlOx thin barrier can be obtained by exposing the Al layer to oxygen plasma, which is available in the vast majority of physical/chemical laboratories. To obtain the information about the energy barrier, one needs to adopt a conventional three-terminal measurement in which one bias voltage is kept fixed and another one is swept—analogous to the basic measurements of any kind of transistors. Furthermore, in Supplementary Figs 4 and 5 we show the results of devices produced ex situ. If gold is employed as the base material, the barrier height can be measured even in a device that was exposed to air for 20 min before the C60 deposition (see also Supplementary Note 2). Without the requirement of in situ deposition, a large variety of metal/semiconductor interfaces can be studied with the present method, including small molecules and polymers deposited via wet methods and solution-processable perovskites. Even lateral geometries for the devices are conceivable and have been demonstrated for inorganic semiconductors33, paving the way to the study of two-dimensional layered systems. Only semiconductors with very low mobility are not suitable in devices similar to those presented since the hot electron current would not diffuse through them. However, the materials of interest for applications in electronics possess relatively high mobility, so even this requirement does not represent a limitation. Furthermore, whereas in this communication we demonstrate only the measurement of the energy barriers for electrons, information on the injection barrier for holes can also be obtained34, extending even further the range of applicability of this method.
In conclusion, we have shown that the energy alignment at metal/molecule interfaces can be measured in a chip by the fabrication of a simple three-terminal device. As a proof of principle, we measured the energy barriers at the interfaces between C60 and different metals. Furthermore, such a device can be used to inject carriers in the organic layer overcoming the contact resistance. This property allows the injection of a highly spin-polarized current into a molecular layer, which would be a breakthrough in the field of spintronics, or studying its conduction properties at very low temperatures, in a range where the contact resistance usually prevents any carrier injection. We anticipate that this scheme for charge injection free from the contact resistance is not limited to bulk semiconductors but can be extended in principle to any semiconductor, including solution-processable and two-dimensional layered semiconductors.
Methods
Device preparation
All the devices described in this communication were fabricated in situ in a UHV dual chamber evaporator (base pressure <10−9 mbar) with a shadow mask system. In the Supplementary Information, we show that even a device produced ex situ has the same electrical behaviour. The sample size is 10 × 10 mm2, and six devices were produced in every sample. Typical device area is 300 × 300 μm2. The measurements were very much reproducible between devices produced in the same evaporation.
Metals were e-beam evaporated in one of the chambers at a rate of 0.1 nm s−1, while C60 was evaporated in the second one from a Knudsen cell at a rate of 2 nm min−1. Metals were 99.95% purity (Lesker), while C60 was of triple-sublimed quality (99.9%) (Sigma Aldrich) and used without further purification.
Electrical characterization
Electrical characterization was performed under vacuum in a variable-temperature probe station (Lakeshore) after the samples had been exposed to air for ~1 min. A Keithley 4200 semiconductor analyser system was used to record I–V.
Additional information
How to cite this article: Gobbi, M. et al. Determination of energy level alignment at metal/molecule interfaces by in-device electrical spectroscopy. Nat. Commun. 5:4161 doi: 10.1038/ncomms5161 (2014).
References
Hwang, J., Wan, A. & Kahn, A. Energetics of metal–organic interfaces: new experiments and assessment of the field. Mater. Sci. Eng. R Rep. 64, 1–31 (2009).
Braun, S., Salaneck, W. R. & Fahlman, M. Energy-level alignment at organic/metal and organic/organic interfaces. Adv. Mater. 21, 1450–1472 (2009).
Friend, R. H. et al. Electroluminescence in conjugated poymers. Nature 397, 121–128 (1999).
Sirringhaus, H. Device physics of solution-processed organic field-effect transistors. Adv. Mater. 17, 2411–2425 (2005).
Lo, M. F. et al. Limits of open circuit voltage in organic photovoltaic devices. Appl. Phys. Lett. 96, 113303 (2010).
Pfeiffer, M., Leo, K. & Karl, N. Fermi level determination in organic thin films by the Kelvin probe method. J. Appl. Phys. 80, 6880 (1996).
Ohno, T. R. et al. C60 bonding and energy-level alignment on metal and semiconductor surfaces. Phys. Rev. B 44, 13747–13755 (1991).
Chase, S. J., Bacsa, W. S., Mitch, M. G., Pilione, L. J. & Lannin, J. S. Surface-enhanced Raman scattering and photoemission of C60 on noble-metal surfaces. Phys. Rev. B 46, 7873–7877 (1992).
Tsuei, K.-D. et al. Photoemission and photoabsorption study of C60 adsorption on Cu(111) surfaces. Phys. Rev. B 56, 15412–15420 (1997).
Maxwell, A. J. et al. Electronic and geometric structure of C60 on Al(111) and A (110). Phys. Rev. B 57, 7312–7326 (1998).
Pedio, M. et al. C60/metal surfaces: adsorption and decomposition. Surf. Sci. 437, 249–260 (1999).
Hayashi, N., Ishii, H., Ouchi, Y. & Seki, K. Examination of band bending at buckminsterfullerene (C[sub 60])/metal interfaces by the Kelvin probe method. J. Appl. Phys. 92, 3784 (2002).
Osikowicz, W., de Jong, M. P. & Salaneck, W. R. Formation of the interfacial dipole at organic-organic interfaces: C60/polymer interfaces. Adv. Mater. 19, 4213–4217 (2007).
Kaiser, W. J. & Bell, L. D. Direct investigation of subsurface interface electronic structure by ballistic-electron-emission microscopy. Phys. Rev. Lett. 60, 1406 (1988).
Bell, L. D. & Kaiser, W. J. Observation of interface band structure by ballistic-electron-emission microscopy. Phys. Rev. Lett. 61, 2368–2371 (1988).
Troadec, C., Kunardi, L. & Chandrasekhar, N. Ballistic emission spectroscopy and imaging of a buried metal/organic interface. Appl. Phys. Lett. 86, 072101 (2005).
Li, W. et al. Ballistic electron emission microscopy studies of Au/molecule/n-GaAs diodes. J. Phys. Chem. B 109, 6252–6256 (2005).
Peumans, P., Yakimov, A. & Forrest, S. R. Small molecular weight organic thin-film photodetectors and solar cells. J. Appl. Phys. 93, 3693 (2003).
Ventrice, C., LaBella, V., Ramaswamy, G., Yu, H. & Schowalter, L. Measurement of hot-electron scattering processes at Au/Si(100) Schottky interfaces by temperature-dependent ballistic-electron-emission microscopy. Phys. Rev. B. Condens. Matter 53, 3952–3959 (1996).
Jansen, R. The spin-valve transistor: a review and outlook. J. Phys. D: Appl. Phys. 36, R289–R308 (2003).
Appelbaum, I., Huang, B. & Monsma, D. J. Electronic measurement and control of spin transport in silicon. Nature 447, 295–298 (2007).
Henderson, G. N., First, P. N., Gaylord, T. K. & Glytsis, E. N. Quantum transmittance from low-temperature ballistic electron emission spectroscopy of Au/Si(100) Schottky interfaces. Phys. Rev. Lett. 71, 2999 (1993).
Gobbi, M. et al. C60-based hot-electron magnetic tunnel transistor. Appl. Phys. Lett. 101, 102404 (2012).
Baldo, M. & Forrest, S. Interface-limited injection in amorphous organic semiconductors. Phys. Rev. B 64, 085201 (2001).
Coropceanu, V. et al. Charge transport in organic semiconductors. Chem. Rev. 107, 926–952 (2007).
Jiang, J., Pearson, J. & Bader, S. Direct determination of energy level alignment and charge transport at metal-Alq3 interfaces via ballistic-electron-emission spectroscopy. Phys. Rev. Lett. 106, 156807 (2011).
Sakanoue, T. & Sirringhaus, H. Band-like temperature dependence of mobility in a solution-processed organic semiconductor. Nat. Mater. 9, 736–740 (2010).
Ma, L., Ouyang, J. & Yang, Y. High-speed and high-current density C60 diodes. Appl. Phys. Lett. 84, 4786 (2004).
Crispin, X. et al. Characterization of the interface dipole at organic/metal interfaces. J. Am. Chem. Soc. 124, 8131–8141 (2002).
Osikowicz, W. et al. Energetics at Au top and bottom contacts on conjugated polymers. Appl. Phys. Lett. 88, 193504 (2006).
Wan, A., Hwang, J., Amy, F. & Kahn, A. Impact of electrode contamination on the α-NPD/Au hole injection barrier. Org. Electron. 6, 47–54 (2005).
Parr, R. G. & Pearson, R. G. Absolute hardness: companion parameter to absolute electronegativity. J. Am. Chem. Soc. 105, 7512–7516 (1983).
Jang, H. & Appelbaum, I. Spin polarized electron transport near the Si/SiO2 interface. Phys. Rev. Lett. 103, 117202 (2009).
Banerjee, T., Haq, E., Siekman, M., Lodder, J. & Jansen, R. Spin filtering of hot holes in a metallic ferromagnet. Phys. Rev. Lett. 94, 027204 (2005).
Acknowledgements
The authors acknowledge Dr S. Parui for fruitful discussions. This work is supported by the European Union 7th Framework Programme under the European Research Council (Grant 257654-SPINTROS), the Marie Curie Actions (PIRG06-GA-2009-256470) and the NMP project (NMP3-SL-2011-263104- HINTS); the Spanish Ministry of Economy under Project No. MAT2012-37638 as well as by the Basque Government through Project No. PI2011-1.
Author information
Authors and Affiliations
Contributions
M.G. designed, carried out and analysed the experiments; L.P. contributed to the data analysis, A.A., A.B.-P., X.S., F.G. and R.L. contributed to the sample preparation and measurement; all the authors participated in the discussion of results and commented on the manuscript. M.G. wrote the paper and L.E.H. supervised the entire study.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-5, Supplementary Notes 1-2 and Supplementary References (PDF 496 kb)
Rights and permissions
About this article
Cite this article
Gobbi, M., Pietrobon, L., Atxabal, A. et al. Determination of energy level alignment at metal/molecule interfaces by in-device electrical spectroscopy. Nat Commun 5, 4161 (2014). https://doi.org/10.1038/ncomms5161
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms5161
This article is cited by
-
Molecular design for enhanced spin transport in molecular semiconductors
Nano Research (2023)
-
Tuning the charge flow between Marcus regimes in an organic thin-film device
Nature Communications (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.