Abstract
Since Shannon derived the seminal formula for the capacity of the additive linear white Gaussian noise channel, it has commonly been interpreted as the ultimate limit of error-free information transmission rate. However, the capacity above the corresponding linear channel limit can be achieved when noise is suppressed using nonlinear elements; that is, the regenerative function not available in linear systems. Regeneration is a fundamental concept that extends from biology to optical communications. All-optical regeneration of coherent signal has attracted particular attention. Surprisingly, the quantitative impact of regeneration on the Shannon capacity has remained unstudied. Here we propose a new method of designing regenerative transmission systems with capacity that is higher than the corresponding linear channel, and illustrate it by proposing application of the Fourier transform for efficient regeneration of multilevel multidimensional signals. The regenerative Shannon limit—the upper bound of regeneration efficiency—is derived.
Similar content being viewed by others
Introduction
Shannon capacity1 defines the maximum amount of error-free information that can be transmitted through a communication channel. Although the linear Shannon limit1 was calculated in 1948, there is no unique nonlinear Shannon limit, as nonlinearity can occur and can be designed and modified in various ways. However, the current existing estimations for lower bounds2,3,4,5 on the Shannon capacity are still referenced as the nonlinear Shannon limit. The calculation of the Shannon capacity for different nonlinear channels is an open and challenging problem.
The existing optical communication systems and technologies, which are primarily responsible for the global data traffic, are facing serious challenges due to nonlinear properties of fibre channels2,3,4,5. It is fair to say that the optical communication sector has reached a bifurcation point and a number of fundamentally new methods to improve information transmission are under investigation around the world (see, for example, refs 6, 7, 8 and references therein). All-optical regeneration, being energy efficient and effective mitigation of noise impairments, attracts attention as a powerful tool for improving quality of signal transmission9,10,11,12,13,14,15,16,17,18,19.
In the current study, we develop a theoretical framework for calculating the Shannon capacity (mutual information optimized over input signal distribution, as defined by Shannon) for nonlinear regenerative channels illustrating it on the example of the proposed regenerative Fourier transform (RFT). Moreover, the maximum gain in Shannon capacity due to regeneration (that is, the Shannon capacity of a system with ideal regenerators—the upper bound on all regenerative schemes) is calculated analytically; thus, the regenerative limit to which the capacity of any regenerative system can be compared, as analogue of the seminal linear Shannon limit, is derived for constructive nonlinearity.
Results
Regenerative mapping
We propose a new technique—the regenerative mapping (see Fig. 1a,b)—for designing the classes of nonlinear communication channels with capacity exceeding the Shannon capacity of the linear additive white Gaussian noise (AWGN) channel. An important new feature introduced by the considered nonlinear mapping is the potential for continuous nonlinear filtering with signal regeneration without requiring a hard decision. This differs from traditional approaches based on ideal regenerators19, which are characterized by step-like piecewise transfer function. The proposed practical example of regenerative mapping incorporates experimentally verified regenerative models12,20 and enables analytical optimization. Whenever the nonlinear transformation has multiple fixed points (Fig. 1c), the consequent interleaving of the accumulating noise with the nonlinear filter produces effective suppression of the noise (see Fig. 1d). The created washboard potential (Fig. 1c) quantizes the signal and improves transmission, with a consequent increase in capacity. A similar idea has been discussed in multiple contexts, ranging from physical systems21 to the interpretation of biological memory effects in terms of potentials with multiple minima22. In quantum theory, a qualitatively similar phenomenon is known as the Zeno effect, where continuous measurement of the quantum system and associated von Neumann collapse of wave function prevents the natural dispersion of the wave function and causes the quantum system to remain in the same state23.
y=T(x)=x+α sin(βx) (a) plotted with fixed β=π shows periodic washboard potential with the slope defined by the parameters; (b) transfer function (TF) with varying α and β at x=π higher intensity is shown by a lighter colour, the optimal values are shown by dashed lines; (c) y=T(x) for the parameters β=π and α=1/β—the optimal set of parameters defines zero slope at the stationary points (maximum noise suppression); (d) Gaussian conditional PDF P(y|x) for the channel with one filter with TF, y=x+π−1 sin(πx) illustrates the regeneration effect at the points defining the signal alphabet.
Consider a regenerative channel with R identical nonlinear filters placed along the transmission line. The cascaded regeneration was demonstrated for various regenerative schemes16,17,18. The signal transmission (for simplicity, signal propagation between the regenerators is assumed to be linear) is distorted by an AWGN that is uniformly distributed along the line, which can be considered as an analogue of the random force in the time-continuous case or noise mixing with the signal during transmission through the media. The regenerative map has a set of special points that are optimal for the nonlinear filtering. The nonlinear transformations y=T(x) (see Fig. 2) result in the effective potential, which creates attraction regions in the signal mapping. When the points are ‘attracted’ to the alphabet, the alphabet should remain stable. This leads to the following set of conditions imposed on the transfer function:
(a) The regenerative transfer functions, plotted for the ideal regenerator and RFT: y=x+α sin(βx) with the alphabet shown by vertical lines; (b) the graphical interpretation of the stability analysis; (c) the scheme with regenerative filters (denoted by F) placed equidistantly along the line; noise distortions are effectively filtered by the ideal regenerators (see constellations before and after noisy transmission with attraction regions shown by straight lines); and (d) numerically calculated Shannon capacity and gain (compared with the linear AWGN channel) for RFT channel with R=20 and R=10 filters (showed by red and green colours, respectively) for both the superstable (dashed-dotted) αβ=1 and stable (dotted) αβ=0.5 mapping. The upper bounds of regeneration efficiency for the given number of the ideal filters R=10 and R=20 are shown by solid green and red curves, respectively.



The first condition means that the alphabet is defined by the stationary points x* of the mapping. Next, the transfer function should change curvature at the alphabet; in other words, the alphabet point is the centre of the attraction region. The third expression reflects the stability condition; that is, the distortion of the signal points is effectively suppressed (see geometry in Fig. 2b). When the first derivative is equal to zero, the alphabet is called superstable.
Regenerative Fourier transform
As an illustration, we propose the regenerative Fourier transform (RFT). The concept of RFT (see Supplementary Fig. 1, Supplementary Note 1) may be generalized to any complete orthogonal system of functions. Without any loss of generality, we use sine functions as the basis for the expansion. The input signal is described by the waveform:  , here summation is performed over the number of symbols, f(t) is a carrier pulse shape and Ts is a symbol period. We apply RFT to each quadrature and add the original and transformed signals:
, here summation is performed over the number of symbols, f(t) is a carrier pulse shape and Ts is a symbol period. We apply RFT to each quadrature and add the original and transformed signals:

Integrated optics-based realization makes FT practically available for numerous emerging applications in optics24,25,26,27,28,29. We show that FT can be used for efficient signal regeneration: RFT. Being the FT of the ideal regenerator, described by the stepwise transfer function, RFT represents the highest achievable regeneration efficiency and can be applied to multilevel multidimensional signals. The RFT mapping is shown in Fig. 2a. According to the previously described optimization procedure, in the considered example the alphabet is placed at the points π(2k+1)/β, where kεZ, that are stable if and only if αβ≤1. In particular, the system is superstable when αβ=1, this gives the optimum parameter values, whereas inequality defines the suboptimal parameters range.
As indicated in ref. 30, it is challenging to regenerate high-order constellations (higher than 32) using the conventional approach of regenerating phase and amplitude, as such constellations have tight phase packing due to energy efficiency requirements. Therefore, a new approach for regenerating separately the two signal quadratures will be required. The proposed RFT is the first scheme to operate on both quadratures and enable an infinite number of regenerative levels. In this sense, this scheme will also potentially enable regeneration of the conventional modulation formats (like, for example, rectangular quadrature amplitude modulation). Moreover, RFT enables the high regeneration efficiency without making a hard decision. The calculated corresponding Shannon capacity shows that such a channel can provide a capacity above the classical Shannon capacity of the linear AWGN channel.
Shannon capacity
The definition of the Shannon capacity for an arbitrary channel (in what follows, capacity C is per unit bandwidth) involves maximizing the mutual information functional1:

over all valid input probability distributions P(x) subject to the power constraint ∬DxP(x)|x|2≤S. Here, the statistical properties of the channel are given by the conditional output–input probability density function (PDF) P(y|x).
Shannon capacity (equation (4)) of the considered systems is a function of the signal-to-noise ratio (SNR), the number of nonlinear filters R and the parameters of nonlinear mapping. SNR is defined here as the ratio of the input signal power S to the noise added linearly to the signal during transmission at each node k=1,…, R: SNR=S/N, where the accumulated noise is given by N=Σ Nk with k being a temporal31,32 or spatial index.
Note that in the nonlinear communication system the definition of the in-line SNR is a nontrivial issue, due to the mixing of signal with noise during propagation. The introduced SNR has the meaning of the signal-to-noise ratio in the respective linear system in the absence of nonlinear in-line elements. This enables the comparison between the performance of the considered system and the corresponding linear AWGN channel with the same noise level. Evidently, the effect of noise squeezing is enhanced as the number of regenerators/nonlinear filters increases (see Fig. 3). To quantify the overall effect, we studied the capacity of the source-destination transmission as a function of the SNR that incorporates the resulting power of all added noise at the source-destination link, which is fundamentally different from the decode-and-forward channel model.
Rectangular M=4 constellations after R consequent RFT transformations interleaved with noise shown (a) at the output of the Rth filter (after RFT transformation) and (b) at the receiving end (when the noise of the last span is added) for the transmission lines having fixed AWGN distortion of SNR=3 dB. The level of noise suppression is more pronounced for the higher number of in-line RFT filters characterized by TF: y=x+π−1 sinπx. Linear unregenerated case R=0 is shown for reference.
The numerically calculated Shannon capacity (mutual information optimized over all input PDF P(x)) is shown in Fig. 2d, which demonstrates visible capacity gain over the Shannon capacity of the linear AWGN channel. In the limit of a large SNR and/or large number of nonlinear filters, all regenerative schemes tend towards asymptotic behaviour, when the gain gap between regenerative and linear AWGN channel capacity is constant. Using the method of steepest descent, we derive the capacity increase for the n-dimensional channel with the RFT transfer function for the suboptimal parameters’ relation (see equation (3)) q=αβ<1:

Regenerative limit
The capacity analysis of the system with the ideal regenerators defines the upper bound of regeneration efficiency. The ideal regenerators assign each transmitted symbol to the closest element of the given alphabet (the corresponding stepwise transfer function is plotted in Fig. 2a by the dashed blue line).
At low SNR range, the Shannon capacity is well approximated by the following expression:

with the transition matrix elements (denote SNR as ρ):  and m±=1−m+.
and m±=1−m+.
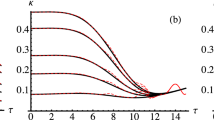
As the SNR increases, the distance between the closest neighbours reaches the optimal cell size, which is defined by the noise variance and the number of in-line regenerators,  , with κ=1+10R−1 and W is the so-called Lambert W function (further, we use normalized value
, with κ=1+10R−1 and W is the so-called Lambert W function (further, we use normalized value  ). Therefore, with the growing signal power, the amplitude distribution remains equidistant, whereas the maximum entropy principle defines Maxwell–Boltzmann distribution as the optimal PDF for a fixed average energy constraint (which is in agreement with performed numerical optimization). Thus, with the growing SNR, a constant gap (that quantifies improvement) can be seen between the regenerative channel and linear AWGN channel capacities (see Supplementary Note 2). The capacity improvement is defined by the noise variance and the number of regenerators:
). Therefore, with the growing signal power, the amplitude distribution remains equidistant, whereas the maximum entropy principle defines Maxwell–Boltzmann distribution as the optimal PDF for a fixed average energy constraint (which is in agreement with performed numerical optimization). Thus, with the growing SNR, a constant gap (that quantifies improvement) can be seen between the regenerative channel and linear AWGN channel capacities (see Supplementary Note 2). The capacity improvement is defined by the noise variance and the number of regenerators:

An additional noise induced from a device itself NT can be incorporated in equation (6), by substituting: N→N+RNT. Moreover, one can estimate a critical value for the noise variance, which can be squeezed by the transformation. By using regenerative mapping technique, it is possible to define a half-width Δ of a plateau (superstable choice of parameters: T′(x*)=0) around an alphabet point x* by solving: T′(x*+Δ)=1 (in particular, for RFT the condition defines:  ). Therefore, the noise is reduced if N/R+NT≤Δ.
). Therefore, the noise is reduced if N/R+NT≤Δ.
The maximum capacity gain due to regeneration (that is, the maximum regeneration efficiency) is observed for the binary channel. The capacity gain reflects the trade-off between the system complexity and capacity improvement. As the number of regenerators increases, the peak of the capacity gain shifts to a smaller SNR. Therefore, employing a low SNR regime and using regeneration, one can achieve high transmission performance with low energy consumption. The minimum SNR value, when dopt is achieved, defines the maximum capacity ratio to its linear analogue; that is,  . At this SNR value, both analytic formulae equations (5) and (6) can be interpolated to describe capacity at the full range of the SNR.
. At this SNR value, both analytic formulae equations (5) and (6) can be interpolated to describe capacity at the full range of the SNR.
Numeric validation
The analytical approximations shown by the black lines in Fig. 4a demonstrate an excellent agreement with the result of numerical computations of the Shannon capacity that exceeds the linear Shannon limit for different number of regenerators (here numerical optimization over input PDF was performed). Figure 4b shows the mutual information (here all symbols were assumed to be equiprobable) for rectangular (left panel) and ring (right panel) packing. Moreover, here we stress the importance of input signal optimization for capacity calculations in nonlinear regenerative channels; otherwise, nonlinearity (even constructive one) will degrade system capacity.
(a) Gain, the regenerative Shannon capacity ratio to the Shannon formula CL=log2(1+ρ), for the different number of regenerators. The analytical results shown by black (dashed) equation 5 and dotted using equation 6) lines demonstrate an excellent agreement with numerics (solid coloured lines). The inset shows mutual information gain for M2—rectangular constellations approaching capacity gain. (b) Capacity and mutual information for discrete M2—rectangular (left panel) and M—points in the ring (right panel) alphabets. The arrows show the constant capacity increase. Constellations and associated attraction regions are shown.
Discussion
Note that the nonlinear regenerative channel is a fundamentally different (to linear AWGN channel) information channel with the constructive use of nonlinearity. In such nonlinear channels, the derived regenerative limit can be considered as the analogue of the Shannon linear limit—it is the maximum error-free transmission rate in regenerative channels. In fibre-optic channels, one can incorporate the impact of Kerr nonlinearity and dispersion on the channel capacity as first-order perturbation, whereas the main order is given by equations (5) and (6). The developed capacity calculation model can generally be applied to various regenerative schemes, where methodology (in Supplementary Note 3, further illustrated on RFT Supplementary Note 4) can be adapted accordingly.
The introduced class of regenerative channels has information capacity that exceeds the Shannon capacity of the linear AWGN channel. The gain is achieved by noise squeezing due to the introduced mapping filter that creates attraction regions around the stable alphabet. The model is generic and the obtained results can be applied to a wide range of physical problems. The results reveal a fascinating new aspect of the interplay between stochastic processes and system nonlinearity, stressing the impact on the channel capacity.
Methods
The Shannon capacity is calculated by defining the conditional PDF, which is expressed through Onsager–Machlup functional or action of the path given by the stochastic map—a discrete version of the Langevin equation for the stochastic processes at each node (see Supplementary Note 3). The detailed description of the capacity functional optimization is given in the Supplementary Note 5.
Additional information
How to cite this article: Sorokina, M. A. and Turitsyn, S. K. Regeneration limit of classical Shannon capacity. Nat. Commun. 5:3861 doi: 10.1038/ncomms4861 (2014).
References
Shannon, C. E. A mathematical theory of communication. Bell Syst. Tech. J. 27, 623–656 (1948).
Mitra, P. P. & Stark, J. B. Nonlinear limits to the information capacity of optical fibre communications. Nature 411, 1027–1030 (2001).
Essiambre, R. J., Foschini, G. J., Kramer, G. & Winzer, P. J. Capacity limits of information transport in fiber-optic networks. Phys. Rev. Lett. 101, 163901 (2008).
Ellis, A. D., Zhao, J. & Cotter, D. Approaching the non-linear Shannon limit. J. Lightwave Technol. 28, 423–433 (2010).
Richardson, D. J. Filling the light pipe. Science 330, 327–328 (2010).
Liu, X. et al. Phase-conjugated twin waves for communication beyond the Kerr nonlinearity limit. Nat. Photon. 7, 560–568 (2013).
Hillerkuss, D. et al. 26 Tbit/s line-rate super-channel transmission utilizing all-optical fast Fourier transform processing. Nat. Photon. 5, 364–371 (2011).
Wang, J. et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photon. 6, 488–496 (2012).
Parmigiani, F. et al. Progress in multichannel all-optical regeneration based on fiber technology. IEEE J. Sel. Top. Quantum Electron. 18, 689–700 (2012).
Vasilyev, M. & Lakoba, T. I. All-optical multichannel 2R regeneration in a fiber-based device. Opt. Lett. 30, 1458–1460 (2005).
Lakoba, T. I. & Vasilyev, M. A new robust regime for a dispersion-managed multichannel regenerator. Opt. Express 15, 10061–10074 (2007).
Boscolo, S., Blow, K. J. & Turitsyn, S. K. All-optical passive 2R regeneration for N × 40 Gbit/s WDM transmission using NOLM and novel filtering technique. Opt. Commun. 217, 227–232 (2003).
Croussore, K., Kim, C. & Li, G. All-optical regeneration of differential phase shift keying signals based on phase-sensitive amplification. Opt. Lett. 29, 2357–2359 (2004).
Slavik, R. et al. All-optical phase and amplitude regenerator for next generation telecommunications systems. Nat. Photon. 4, 690–695 (2010).
Kakande, J. et al. Multilevel quantization of optical phase in a novel coherent parametric mixer architecture. Nat. Photon. 5, 748–752 (2011).
Nakazawa, M., Yamada, E., Kubota, H. & Suzuki, K. 10 Gbit/s soliton data transmission over one million kilometres. Electron. Lett. 27, 1270–1272 (1991).
Matsumoto, M. Fiber-based all-optical signal regeneration. IEEE J. Sel. Top. Quantum Electron. 18, 738–752 (2012).
Umeki, T. et al. Multi-span transmission using phase and amplitude regeneration in PPLN-based PSA. Opt. Express 21, 18170–18177 (2013).
Turitsyn, K. S. & Turitsyn, S. K. Nonlinear communication channels with capacity above the linear Shannon limit. Opt. Lett. 37, 3600–3602 (2012).
Sorokina, M. A., Sygletos, S. & Turitsyn, S. K. Optimization of cascaded regenerative links based on phase sensitive amplifiers. Opt. Lett. 38, 4378–4381 (2013).
Martinis, J. M., Devoret, M. H. & Clarke, J. Energy-level quantization in the zero-voltage state of a current-biased Josephson junction. Phys. Rev. Lett. 55, 1543–1546 (1985).
Angeli, D., Ferrell, J. F. & Sontag, E. D. Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. Proc. Natl Acad. Sci. USA 101, 1822–1827 (2004).
Koshino, K. & Shimizu, A. Quantum Zeno effect by general measurements. Phys. Rep. 412, 191–275 (2005).
Siegman, A. E. Fiber Fourier optics. Opt. Lett. 26, 1215–1217 (2001).
Nakazawa, M. et al. Ideal distortion-free transmission using optical Fourier transformation and Fourier transform-limited optical pulses. IEEE Photon. Technol. Lett. 16, 1059–1061 (2004).
Guan, P. et al. Single-channel 1.28 Tbit/s-525 km DQPSK transmission using ultrafast time-domain optical Fourier transformation and nonlinear optical loop mirror. IEICE Trans. Commun. 94-b, 430–436 (2011).
Hillerkuss, D. et al. Simple all-optical FFT scheme enabling Tbit/s real-time signal processing. Opt. Express 18, 9324–9340 (2010).
Mulvad, H. C. H. et al. Ultra-high-speed optical serial-to-parallel data conversion by time-domain optical Fourier transformation in a silicon nanowire. Opt. Express 19, B825–B835 (2011).
Chen, H. et al. 5 × 200 Gbit/s all-optical OFDM transmission using a single optical source and optical Fourier transform real-time detection. Opt. Express 19, 21199–21204 (2011).
Sorokina, M. A. Design of multilevel amplitude regenerative system. Opt. Lett. 39, 2499–2502 (2014).
Crutchfield, J. R., Nauenberg, M. & Rudnick, J. Scaling for external noise at the onset of chaos. Phys. Rev. Lett. 46, 933–935 (1981).
Reimann, P. & Talkner, P. Probability densities for discrete dynamical systems with weak noise. Helv. Phys. Acta 63, 845–846 (1991).
Acknowledgements
We are grateful to K.S. Turitsyn, E. Narimanov, S. Sygletos and A.D. Ellis for fruitful discussions. The support under the UK EPSRC Programme Grant UNLOC EP/J017582/1 is acknowledged.
Author information
Authors and Affiliations
Contributions
S.K.T. initiated the project. M.A.S. and S.K.T. derived the results, contributed to manuscript preparation and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figure 1, Supplementary Notes 1-5 and Supplementary References (PDF 662 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Sorokina, M., Turitsyn, S. Regeneration limit of classical Shannon capacity. Nat Commun 5, 3861 (2014). https://doi.org/10.1038/ncomms4861
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms4861
This article is cited by
-
All-optical regenerator of multi-channel signals
Nature Communications (2017)
-
Spectral correlations in a random distributed feedback fibre laser
Nature Communications (2017)
-
Stochasticity, periodicity and localized light structures in partially mode-locked fibre lasers
Nature Communications (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.