Abstract
Ecosystems can undergo sudden shifts to undesirable states, but recent studies with simple single-species ecosystems have demonstrated that advance warning can be provided by the slowing down of population dynamics near a tipping point. However, it is unclear how this ‘critical slowing down’ will manifest in ecosystems with strong interactions between their components. Here we probe the dynamics of an experimental producer-freeloader ecosystem as it approaches a catastrophic collapse. Surprisingly, the producer population grows in size as the environment deteriorates, highlighting that population size can be a misleading measure of ecosystem stability. By analysing the oscillatory producer-freeloader dynamics for over 100 generations in multiple environmental conditions, we find that the collective ecosystem dynamics slow down as the tipping point is approached. Analysis of the coupled dynamics of interacting populations may therefore be necessary to provide advance warning of collapse in complex communities.
Similar content being viewed by others
Introduction
Climate change and overexploitation of natural resources are altering many of the earth’s ecosystems, often leading to habitat loss and species extinction. These regime shifts in ecological systems can occur without obvious warning; and once they have transpired, they may be extremely difficult to reverse, even after the agent that caused them is identified and removed1,2,3,4,5,6. This irreversibility is a consequence of the ecosystem undergoing a critical transition, in which it switches from one stable state to another. Once this happens, the feedback loops that stabilize the new state make it difficult to reverse the transition, leading to memory effects or hysteresis1,2,7.
As ecosystems approach such critical transitions they may often lose resilience, making it easier for external perturbations to induce a regime shift8. Given the negative consequences of these unwanted regime shifts, there is a desire to measure the stability of ecosystems and identify early warning indicators preceding catastrophic transitions. Recently, there has been growing interest in using bifurcation theory7,9,10,11 and the signatures of critical slowing down12,13 (a phenomenon well studied in physics14,15 and many other fields16,17,18,19,20,21,22) as a paradigm to understand the dynamics before transitions between alternative stable states in ecosystems. Theory further suggests that the loss of resilience of an ecosystem as it approaches a tipping point should be accompanied by a slowing down of the collective dynamics of the ecosystem1,8,23,24,25. This prediction has been confirmed in single-species laboratory microcosms, where critical slowing down and its indirect signatures (for example, increases in population variability and the correlation of fluctuations) have been observed26,27,28.
In parallel with the studies of simple laboratory populations, early warning indicators based on critical slowing down have been studied in models of complex ecosystems2,6,26,29,30. Indeed, it is expected that sudden transitions will be common in ecological networks with multiple interacting species2. Theoretical analysis of concrete ecosystems with either two23 or three29 strongly interacting species concluded that the collapse of more complex ecosystems may also be preceded by critical slowing down—in this case manifested as the dominant eigenvalue of the community matrix approaching zero30 (or one, for temporally discretized dynamics31). Encouragingly, recent experiments of exceedingly complex lake ecosystems indicate that the effects of critical slowing down may be seen by investigating the dynamics of individual species, or indirect reporters of the presence of other species32,33. Nevertheless, how critical transitions take place in complex ecological networks is still poorly understood; for instance, as to how the inter-specific interactions within the ecosystem34 affect the collective dynamics on the brink of a regime shift, or which particular indicator will exhibit the strongest signatures of critical slowing down. To address these questions, and to understand how early warning indicators behave in ecosystems with strong interactions between species, we set out to study the dynamics of a laboratory producer-freeloader ecosystem consisting of two yeast strains with different phenotypes.
Our producer-freeloader ecosystem consists of two different strains of budding yeast (Saccharomyces cerevisiae) growing on sucrose. Budding yeast requires the enzyme invertase to break down sucrose into glucose and fructose. Invertase is secreted into the periplasmic space between the cell membrane and the cell wall. Due to this secretion outside of the cell, 99% of the glucose and fructose diffuse away from the cell that produced them, and can be consumed by other cells in the population35. In our experiments, the ‘producer’ strain expresses the SUC2 gene that encodes for invertase production; the second yeast strain, the ‘freeloader’ lacks this gene and does not contribute to the breakdown of sucrose. Thus, the freeloader population exploits the producer population by consuming glucose and fructose without paying the metabolic cost associated with their production. This experimental system has been previously characterized as a model of the public-goods evolutionary game dynamics between cooperators and cheaters35,36,37,38,39. This evolutionary intra-species interaction is a particular realization of a more general ecological interaction where one species (a producer) produces a resource that is also consumed by individuals that benefit from it but which have not contributed to its production (freeloaders). Mathematically, the cooperator–cheater dynamics has been shown to be equivalent to the dynamics between producers and freeloaders (or prey and predators)36,40.
Results
Collapse of an experimental producer-freeloader ecosystem
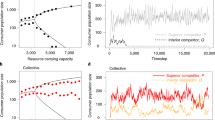
Based on prior experiments with monocultures of the producer strain in sucrose media27, we expected our producer-freeloader ecosystem to exhibit a critical collapse as the environment deteriorates. To test this, we grew replicate co-cultures of the two yeast strains in sucrose media, and subjected the cultures to multiple daily cycles of growth-dilution (see Methods). This experimental design naturally introduces an experimentally tunable dilution factor (DF), akin to a mortality rate, which was our control parameter for environmental deterioration27,36. We followed the ecosystems for nine days and measured the density of the producer and freeloader populations after each growth-dilution cycle. Our observations are consistent with the presence of a tipping point in our ecosystem located around a DF of 2,000: below that DF the populations found a stable equilibrium, but when the DF was increased beyond this value, the populations collapsed and went extinct (Fig. 1).
(a) Yeast populations were grown in sucrose media and subjected to a range of daily dilution factors. Experiments were started with identical initial concentrations of producers (which carry the gene SUC2 required for sucrose break down) and freeloaders (SUC2 knockouts). (b) The equilibrium population density of the producer (green) and freeloader (red) populations as a function of dilution factor. Error bars represent s.e.m. (n=20). The producer population size increases as the environment deteriorates, highlighting that population size is not always a reliable indicator of population health.
In previous experimental studies in monocultures26,27,28, the population size always declined with environment deterioration. In particular, this was the case for cultures of our producer strain in isolation27. In contrast, here we found that in the face of competition with the freeloader strain (whose population size does show the expected decline) the producer population increased in size as the environment deteriorated, and was maximal in the proximity of the tipping point (Fig. 1b). This increase in population size of the producer population as the environment deteriorates is a consequence of the nonlinear coupled dynamics in the system (Supplementary Fig. 1); at high DFs, the lower density of freeloaders leads to weaker competitive interactions and allows for less hindered growth of the producers. Species interactions may therefore lead to counter-intuitive changes at the ecosystem level as the environment deteriorates. Thus, in contrast to simple single-species ecosystems, changes in the population size of any individual species are not necessarily a reliable indicator of loss of resilience in a complex ecosystem.
Loss of ecological resilience may be foreseen by critical slowing down
As a warning indicator of tipping points in an ecosystem, critical slowing down is manifested in the collective dynamics of the whole ecosystem; in particular, it is characterized by the dominant eigenvalue of the linearized discrete dynamics around equilibrium (that is, the interaction matrix31). The absolute value of the dominant eigenvalue of the interaction matrix describing the discrete dynamics is expected to approach |λdom|=1 as the system approaches a critical transition23.
To observe the coupled dynamics in our population, we plotted the trajectories followed by the ecosystem on the producer-freeloader phase plane (Fig. 2). Consistent with previous experiments36, the trajectories spiralled to an equilibrium at which the two populations coexist. The observed damped oscillations is a hallmark of the coupled dynamics resulting from the interactions between producers and freeloaders41,42,43,44,45,46,47. Given our experimental resolution and the level of noise, we cannot entirely rule out the possible existence of a very small limit cycle, but our data of population trajectories at equilibrium in a longer experiment (Supplementary Fig. 2e) as well as the dynamics in simulations (Supplementary Fig. 3) indicate that our system converged to a stable fixed point. We estimated the equilibrium point in the producer-freeloader phase plane (Supplementary Fig. 4), and fit the spirals to a first-order multivariate autoregressive model to obtain an estimate for the interaction matrix, from which the eigenvalues could be calculated (see Methods). As expected from the spiralling trajectories, the eigenvalues had both a real and an imaginary component. For the trajectory plotted in Fig. 2, corresponding to a DF of 1,333, we found λ1,2=|λ|e±iθ, where |λ|=0.83±0.11 and θ=39°±6°. For these spiralling trajectories, the magnitude of the eigenvalue |λ| specifies how rapidly the trajectories radially converge to the equilibrium, whereas the angle θ reflects how quickly the trajectories spiral tangentially around the equilibrium. The theory of critical slowing down predicts that |λ| should increase, approaching ~1 as the ecosystem approaches the tipping point of a critical transition. This means that as the environment deteriorates it takes longer for the two subpopulations to reach equilibrium23.
(a) The dynamics of the population density can be visualized as trajectories in the producer-freeloader phase plane. Replicate populations were grown from 30 different starting densities with a daily dilution of 1,333 for 14 days. Selected trajectories are coloured consistently on the three plots, with remaining trajectories shown in light grey. The indicated blue trajectory has complex eigenvalues λ=0.83 e±i 39°. The individual dynamics of the producers (b) and the freeloaders (c) are plotted as a function of time (both are expressed in units of 106 cells ml−1).
To test these theoretical predictions, we subjected our producer-freeloader ecosystems to eight different DFs, ranging from 50 to 1,600. Thirty replicate ecosystems were tracked for each DF. As expected, the absolute magnitude of the eigenvalue increased substantially as the environmental quality decreased, and approached |λ|=1 just before population collapse (Fig. 3). Thus, our direct observation of critical slowing down in an experimental producer-freeloader ecosystem lends support to the linearization approach in assessing community stability and species interactions31, as well as using the dominant eigenvalue of the interaction matrix as a warning signal in multi-species ecosystems. We are not aware of any theoretical predictions regarding the behaviour of θ (argument of eigenvalues) as the tipping point is approached, and indeed we did not observe any noticeable change in θ (Supplementary Fig. 2e).
Thirty replicate populations with varying initial conditions were grown at each of eight different daily dilution factors. Their spiralling trajectories were analysed to estimate their eigenvalues (generally a pair of complex conjugates). As predicted by theory, the magnitude of the eigenvalues increases and approaches one as the environment deteriorates. Dilution factors above 1,600 were not assessed due to the difficulty of calculating eigenvalues from very noisy data (see DF 2,000 in Fig. 4). Error bars represent standard error and were obtained by bootstrapping the experimental trajectories as well as the location of the fixed point with 50 resamplings.
Indirect early warning indicators at the single-species level
Previous analyses of natural ecosystems had indicated that individual species may exhibit behaviours consistent with critical slowing down as the ecosystem approaches a bifurcation32. Mathematical analysis of the dynamics of a general two-species ecosystem reveals that the variability in the fluctuations of population density of each species is expected to diverge when |λ| approaches 1 near a tipping point31 (Supplementary Note 1). Therefore, statistical indicators based on the size of fluctuations in the population density of individual species may provide indirect signatures of critical slowing down at the ecosystem level. To test this, we measured the coefficient of variation (CV) between replicates on the final day of the experiment for both the producer and freeloader populations (see Methods). We found that the CV increased sharply with rising DFs for both producer and freeloader populations (Fig. 4). Therefore, variability in the density of either species across replicates provides an early warning signal of the approaching tipping point in our producer-freeloader ecosystem, even when the equilibrium population density increases (which is the case for our producer population).
The coefficient of variation (CV) measured for both producer (green) and freeloader (red) populations as a function of dilution factor. Populations were grown from the same initial density of producers and freeloaders, and the coefficient of variation across the 20 replicates for each dilution factor was measured on the final day of the experiment (day 9). Inset figures represent the time series of the producer density (measured in 106 cells ml−1) of each replicate at a low dilution factor (left panel) and a high dilution factor (right panel). Similar results were found for the freeloader populations. Error bars are standard errors obtained by bootstrapping with 100 resamplings.
Several other indicators of critical slowing down have been proposed theoretically and some observed experimentally in monocultures1,2,26,27,28. They include the deterministic return time following a pulse perturbation and the lag-1 autocorrelation of the fluctuations of the population density. In our experiments with a relatively small sample size, both the deterministic return time and the lag-1 autocorrelation based on single-species time series failed to produce statistically significant increases with an increasing DF (Supplementary Figs 2c,d and 5). In a previous experiment with monocultures of the producer population27, we observed a clear increase in the CV, lag-1 autocorrelation and return time before population collapse. Our experiments and mathematical analysis reported here suggest that certain warning indicators based on a single species may fail in the presence of interactions between species (Supplementary Notes 1 and 2). This failure of some indicators based on single-species data highlights the importance of understanding species interactions in the application of early warning indicators to complex ecosystems; it also supports the notion that stability is a property of the entire community instead of its constituent species48. Although properties of the whole community may not always be inferred from a single species, replicate laboratory ecosystems can help to elucidate the warning indicators that will be most useful and reliable in real-world settings.
Discussion
Our study represents an initial characterization of population dynamics near a regime shift in an ecological network with strong inter-species interactions. Due to the impracticality of assessing unstable systems, it is difficult to determine the exact nature of the transition. Our model predicts a Hopf bifurcation (Supplementary Fig. 3), which exhibits critical slowing down near its tipping point6. Although our system is two-dimensional, it is worth noting that bifurcations in higher dimensions can be extraordinarily rich and complex9. Even in low-dimensional systems, not all bifurcations lead to critical slowing down, and regime shifts may occur with no warning49,50,51. On the other hand, recent theoretical studies have pointed out that, in some instances, critical slowing down can be detected even in the absence of any critical transitions50,52,53. In spite of these potential caveats in using critical slowing down to forecast ecological regime shifts, our experiments demonstrate that it may be possible to observe the dominant eigenvalue of the interaction matrix increasing and approaching 1 before the collapse of a producer-freeloader ecosystem, and provide support to the utility of critical slowing down as a warning signal in multi-species ecosystems23,48,54. We also recognize that there are other alternative indices based on the interaction matrix, which may prove useful in quantifying the transient dynamics48,55.
In many ecosystems it may not be possible to study the collective dynamics of the whole system and obtain the eigenvalues, as that would require tracking the dynamics for each of the interacting species. However, our optimism in understanding complex ecosystems come from the belief that many ecosystems may consist of loosely coupled units with low dimensionality56. Recent experiments in a whole-lake ecosystem32 provided evidence that some warning indicators can be observed based on time series of individual species within a multi-species ecosystem. In spite of this favourable empirical example, we caution that analysing any single species in an ecosystem does not necessarily provide reliable warning indicators, especially when the coupling between species leads to oscillatory dynamics, as seen in this study. Our study underscores the necessity of characterizing species interactions and collective dynamics when applying early warning signals to complex ecosystems. More quantitative studies in multi-species systems, especially in spatially extended contexts24,57,58,59, will shed light on how to monitor a complex ecosystem to maximize the utility of early warning indicators.
Methods
Strains
The producer strain, JG300A35, is derived from BY4741 strain of S. cerevisiae (mating type a, EUROSCARF) that has a wild-type SUC2 gene. It constitutively expresses YFP from the ADH1 promoter (inserted using plasmid pRS401, with a MET17 marker), and also has a mutated HIS3 (his3Δ1). The freeloader strain, JG210C35, is a SUC2 deletion strain (EUROSCARF Y02321, SUC2::kanMX4) of S. cerevisiae. It constitutively expresses dTomato from the PGK1 promoter (inserted using plasmid pRS301, with a HIS3 marker).
Culture growth
The growth medium was composed of synthetic media (YNB and CSM-his; Sunrise Science, California), 2% sucrose, 0.001% glucose and 8 μg ml−1 histidine36. Cells were cultured in 200 μl of media within the 60 internal wells of a Falcon flat-bottom 96-well plate (BD Biosciences, California), with the 36 external wells filled with 200 μl growth media36. The plates were incubated at 30 °C, while being shaken at 800 r.p.m. During incubation, the plates were covered with Parafilm as well as the plate cover. Cultures were subject to growth-dilution cycles36, where cells were allowed to grow for 23.5 h and then diluted by a predetermined DF. The cultures were then incubated again, beginning a new day’s cycle.
Measurement of population densities
The optical density of each culture at 620 nm was measured with a Thermo Scientific Multiskan FC microplate spectrophotometer, following the end of each growth period27. To measure the fractions of each population, at the end of each growth period a portion of cells from each well (typically 5 μl, unless the low density conditions made it necessary to transfer larger volumes) was transferred to a new plate containing 200 μl sterile Cellgro PBS buffer (Mediatech, Virginia). These samples were then analysed at a BD LSRII-HTS flow cytometer operating in high throughput mode, where we determined the ratio between the producer and freeloader strains, distinguished by their fluorescence emissions36. Given the total density and the strain ratio, the densities of the producer and freeloader populations were readily calculated.
Calculation of CV
CV was calculated for each subpopulation by dividing the standard deviation of the final-day population by the final-day sample mean. Populations that were dying or dead were filtered out, as per Supplementary Note 3. Errors were estimated by bootstrapping, with 100 resamplings.
Calculation of eigenvalues
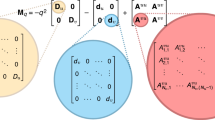
The eigenvalues of the system are calculated by linearizing the dynamics of the trajectories around the equilibrium point. Because we observe the producer and freeloader populations in discrete time intervals (once per day), we can model their motion on the producer-freeloader phase plane by a difference equation:

where (xt, yt) is the vector containing the producer (X) and freeloader (Y) populations on day t. (X*, Y*) is the equilibrium point of the trajectory, and J is the 2 × 2 Jacobian matrix (or ‘interaction matrix’) that describes the dynamics on the producer-freeloader phase plane. Each day, this Jacobian matrix is applied to the previous day’s population vector (Xt, Yt) to generate the next day’s set of producer and freeloader densities (Xt+1, Yt+1). Notice that this is a linear transformation, which is not an exact reflection of the nonlinear dynamics for the entire phase plane. However, in the vicinity of a fixed point (as in our experiments), we may choose to retain only the first-order terms of the Taylor expansion of the true transformation. The ensuing linear system is thus a reasonable approximation to our spiralling trajectories near the fixed point.
Once we determine our best estimate for the matrix J, we can perform an eigendecomposition to calculate its eigenvalues (assuming that the Jacobian matrix is not defective):

where λ1 and λ2 are the eigenvalues of J, and P is the matrix whose columns are the two eigenvectors of J. To determine J from our experimental data, we took two approaches in fitting the trajectories as per equation (1), which are further described in Supplementary Note 4.
Additional information
How to cite this article: Chen, A. et al. Dynamics of a producer-freeloader ecosystem on the brink of collapse. Nat. Commun. 5:3713 doi: 10.1038/ncomms4713 (2014).
References
Scheffer, M. et al. Early-warning signals for critical transitions. Nature 461, 53–59 (2009).
Scheffer, M. et al. Anticipating critical transitions. Science 338, 344–348 (2012).
Scheffer, M., Carpenter, S., Foley, J. A., Folke, C. & Walker, B. Catastrophic shifts in ecosystems. Nature 413, 591–596 (2001).
Folke, C. et al. Regime shifts, resilience, and biodiversity in ecosystem management. Annu. Rev. Ecol. Evol. Syst. 35, 557–581 (2004).
Petraitis, P. Multiple Stable States in Natural Ecosystems Oxford Univ. Press (2013).
Seekell, D. A., Cline, T. J., Carpenter, S. R. & Pace, M. L. Evidence of alternate attractors from a whole-ecosystem regime shift experiment. Theor. Ecol. 6, 385–394 (2013).
Strogatz, S. Nonlinear Dynamics and Chaos Westview (1994).
Van Nes, E. H. & Scheffer, M. Slow recovery from perturbations as a generic indicator of a nearby catastrophic shift. Am. Nat. 169, 738–747 (2007).
Kuznetsov, Y. Elements of Applied Bifurcation Theory Springer (2004).
Gilmore, R. Catastrophe Theory for Scientists and Engineers Courier Dover Publications (1993).
Zahler, R. S. & Sussmann, H. J. Claims and accomplishments of applied catastrophe theory. Nature 269, 759–763 (1977).
Kuehn, C. A mathematical framework for critical transitions: Bifurcations, fast–slow systems and stochastic dynamics. Physica D 240, 1020–1035 (2011).
Wissel, C. A universal law of the characteristic return time near thresholds. Oecologia 65, 101–107 (1984).
Hohenberg, P. C. & Halperin, B. I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 49, 435–479 (1977).
Suzuki, M., Kaneko, K. & Sasagawa, F. Phase transition and slowing down in non-equilibrium stochastic processes. Prog. Theor. Phys. 65, 828–849 (1981).
Stanley, H. E., Nunes Amaral, L. A., Gabaix, X., Gopikrishnan, P. & Plerou, V. Quantifying economic fluctuations. Physica A 302, 126–137 (2001).
Kleinen, T., Held, H. & Petschel-Held, G. The potential role of spectral properties in detecting thresholds in the Earth system: application to the thermohaline circulation. Ocean Dyn. 53, 53–63 (2003).
Kramer, J. & Ross, J. Stabilization of unstable states, relaxation, and critical slowing down in a bistable system. J. Chem. Phys. 83, 6234 (1985).
Livina, V. N. & Lenton, T. M. A modified method for detecting incipient bifurcations in a dynamical system. Geophys. Res. Lett. 34, L03712 (2007).
Nitzan, A. Chemical instabilities as critical phenomena. Phys. Rev. A 17, 1513–1528 (1978).
Scholz, J. P., Kelso, J. A. S. & Schöner, G. Nonequilibrium phase transitions in coordinated biological motion: critical slowing down and switching time. Phys. Lett. A 123, 390–394 (1987).
Steyn-Ross, D. A., Steyn-Ross, M. L., Wilson, M. T. & Sleigh, J. W. White-noise susceptibility and critical slowing in neurons near spiking threshold. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 74, 051920 (2006).
Chisholm, R. A. & Filotas, E. Critical slowing down as an indicator of transitions in two-species models. J. Theor. Biol. 257, 142–149 (2009).
Dakos, V. et al. Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS ONE 7, e41010 (2012).
Dakos, V., van Nes, E. H., D’Odorico, P. & Scheffer, M. Robustness of variance and autocorrelation as indicators of critical slowing down. Ecology 93, 264–271 (2012).
Drake, J. M. & Griffen, B. D. Early warning signals of extinction in deteriorating environments. Nature 467, 456–459 (2010).
Dai, L., Vorselen, D., Korolev, K. S. & Gore, J. Generic indicators for loss of resilience before a tipping point leading to population collapse. Science 336, 1175–1177 (2012).
Veraart, A. J. et al. Recovery rates reflect distance to a tipping point in a living system. Nature 481, 357–359 (2012).
Lade, S. J. & Gross, T. Early warning signals for critical transitions: a generalized modeling approach. PLoS Comput. Biol. 8, e1002360 (2012).
May, R. M. Stability and Complexity in Complex Ecosystems Princeton Uni. Press (2001).
Ives, A. R., Dennis, B., Cottingham, K. L. & Carpenter, S. R. Estimating community stability and ecological interactions from time-series data. Ecol. Monogr. 73, 301–330 (2003).
Carpenter, S. R. et al. Early warnings of regime shifts: a whole-ecosystem experiment. Science 332, 1079–1082 (2011).
Carpenter, S. R., Brock, W. A., Cole, J. J., Kitchell, J. F. & Pace, M. L. Leading indicators of trophic cascades. Ecol. Lett. 11, 128–138 (2008).
Thrush, S. F. et al. Forecasting the limits of resilience: integrating empirical research with theory. Proc. Biol. Sci. 276, 3209–3217 (2009).
Gore, J., Youk, H. & van Oudenaarden, A. Snowdrift game dynamics and facultative cheating in yeast. Nature 459, 253–256 (2009).
Sanchez, A. & Gore, J. feedback between population and evolutionary dynamics determines the fate of social microbial populations. PLoS Biol. 11, e1001547 (2013).
Koschwanez, J. H., Foster, K. R. & Murray, A. W. Sucrose utilization in budding yeast as a model for the origin of undifferentiated multicellularity. PLoS Biol. 9, e1001122 (2011).
Greig, D. & Travisano, M. The prisoner’s dilemma and polymorphism in yeast SUC genes. Proc. Biol. Sci. 271, (Suppl 3): S25–S26 (2004).
MaClean, R. C., Fuentes-Hernandez, A., Greig, D., Hurst, L. D. & Gudelj, I. A mixture of ‘cheats’ and ‘co-operators’ can enable maximal group benefit. PLoS Biol. 8, e1000486 (2010).
Hofbauer, J. & Sigmund, K. Evolutionary Games and Population Dynamics Cambridge Univ. Press (1998).
De Aguiar, M. A. M., Rauch, E. M. & Bar-Yam, Y. Mean-field approximation to a spatial host-pathogen model. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 67, 047102 (2003).
Hauert, C., Holmes, M. & Doebeli, M. Evolutionary games and population dynamics: maintenance of cooperation in public goods games. Proc. R. Soc. B 273, 2565–2571 (2006).
McKane, A. J. & Newman, T. J. Predator-prey cycles from resonant amplification of demographic stochasticity. Phys. Rev. Lett. 94, 218102 (2005).
Rosenzweig, M. & Macarthur, R. Graphical representation and stability conditions of predator-prey interactions. Am. Nat. 97, 209 (1963).
Vandermeer, J. H. & Goldberg, D. E. Population Ecology: First Principles Princeton Univ. Press (2003).
Wang, Z. & Goldenfeld, N. Fixed points and limit cycles in the population dynamics of lysogenic viruses and their hosts. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 82, 011918 (2010).
Weitz, J. S. & Dushoff, J. Alternative stable states in host–phage dynamics. Theor. Ecol. 1, 13–19 (2008).
Ives, A. R. Measuring resilience in stochastic systems. Ecol. Monogr. 65, 217–233 (1995).
Boettiger, C., Ross, N. & Hastings, A. Early warning signals: the charted and uncharted territories. Theor. Ecol. 6, 255–264 (2013).
Boettiger, C. & Hastings, A. Tipping points: from patterns to predictions. Nature 493, 157–158 (2013).
Ditlevsen, P. D. & Johnsen, S. J. Tipping points: early warning and wishful thinking. Geophys. Res. Lett. 37, 2–5 (2010).
Kéfi, S., Dakos, V., Scheffer, M., Van Nes, E. H. & Rietkerk, M. Early warning signals also precede non-catastrophic transitions. Oikos 122, 641–648 (2013).
Boettiger, C. & Hastings, A. Early warning signals and the prosecutor’s fallacy. Proc. Biol. Sci. 279, 4734–4739 (2012).
Batt, R. D. et al. Asymmetric response of early warning indicators of phytoplankton transition to and from cycles. Theor. Ecol. 6, 285–293 (2013).
Neubert, M. G. & Caswell, H. Alternatives to resilience for measuring the responses of ecological systems to perturbations. Ecology 78, 653–665 (1997).
May, R. M. Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature 269, 471–477 (1977).
Dai, L., Korolev, K. S. & Gore, J. Slower recovery in space before collapse of connected populations. Nature 496, 355–358 (2013).
Bailey, R. M. Spatial and temporal signatures of fragility and threshold proximity in modelled semi-arid vegetation. Proc. Biol. Sci. 278, 1064–1071 (2011).
Streeter, R. & Dugmore, A. J. Anticipating land surface change. Proc. Natl Acad. Sci. USA 110, 5779–5784 (2013).
Acknowledgements
We thank all members of the Gore lab for useful comments and discussion. This work was supported by grant FQEB #RFP-12-07, NIH grants NIH DP2 and R00 GM085279-02, as well as grant PHY-1055154 from the NSF. We also received support from the Pew Foundation, Alfred P. Sloan Foundation and the Paul Allen Foundation.
Author information
Authors and Affiliations
Contributions
The authors have made the following declarations about their contributions. A.S. and J.G. designed the experiments. A.C. performed the experiments. A.C. and A.S. analysed the data. A.C., A.S. and L.D. performed the simulations. A.C., A.S., L.D. and J.G. wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-6, Supplementary Table 1, Supplementary Notes 1-7 and Supplementary References (PDF 1264 kb)
Rights and permissions
About this article
Cite this article
Chen, A., Sanchez, A., Dai, L. et al. Dynamics of a producer-freeloader ecosystem on the brink of collapse. Nat Commun 5, 3713 (2014). https://doi.org/10.1038/ncomms4713
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms4713
This article is cited by
-
Disentangling reporting and disease transmission
Theoretical Ecology (2019)
-
When increasing population density can promote the evolution of metabolic cooperation
The ISME Journal (2018)
-
Ecological effects of cellular computing in microbial populations
Natural Computing (2018)
-
Synthetically engineered microbes reveal interesting principles of cooperation
Frontiers of Chemical Science and Engineering (2017)
-
Detecting the Collapse of Cooperation in Evolving Networks
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.