Abstract
In the quest to increase the critical temperature Tc of cuprate superconductors, it is essential to identify the factors that limit the strength of superconductivity. The upper critical field Hc2 is a fundamental measure of that strength, yet there is no agreement on its magnitude and doping dependence in cuprate superconductors. Here we show that the thermal conductivity can be used to directly detect Hc2 in the cuprates YBa2Cu3Oy, YBa2Cu4O8 and Tl2Ba2CuO6+δ, allowing us to map out Hc2 across the doping phase diagram. It exhibits two peaks, each located at a critical point where the Fermi surface of YBa2Cu3Oy is known to undergo a transformation. Below the higher critical point, the condensation energy, obtained directly from Hc2, suffers a sudden 20-fold collapse. This reveals that phase competition—associated with Fermi-surface reconstruction and charge-density-wave order—is a key limiting factor in the superconductivity of cuprates.
Similar content being viewed by others
Introduction
In a type-II superconductor at T=0, the onset of the superconducting state as a function of decreasing magnetic field H occurs at the upper critical field Hc2, dictated by the pairing gap Δ through the coherence length ξ0~vF/Δ, via Hc2=Φ0/2πξ02, where vF is the Fermi velocity and Φ0 is the magnetic flux quantum. Hc2 is the field below which vortices appear in the sample. Typically, the vortices immediately form a lattice (or solid) and thus cause the electrical resistance to go to zero. So the vortex-solid melting field, Hvs, is equal to Hc2. In cuprate superconductors, the strong 2D character and low superfluid density cause a vortex liquid phase to intervene between the vortex-solid phase below Hvs(T) and the normal state above Hc2(T) (ref. 1). It has been argued that in underdoped cuprates there is a wide vortex-liquid phase even at T=0 (refs 2, 3, 4, 5), so that Hc2(0)>>Hvs(0), implying that Δ is very large. Whether the gap Δ is large or small in the underdoped regime is a pivotal issue for understanding what controls the strength of superconductivity in cuprates. So far, however, no measurement on a cuprate superconductor has revealed a clear transition at Hc2, so there are only indirect estimates2,6,7 and these vary widely (see Supplementary Discussion and Supplementary Fig. 1). For example, superconducting signals in the Nernst effect2 and the magnetization4 have been tracked to high fields, but it is difficult to know whether these are due to vortex-like excitations below Hc2 or to fluctuations above Hc2 (ref. 7).
Here we demonstrate that measurements of the thermal conductivity can directly detect Hc2, and we show that in the cuprate superconductors YBa2Cu3Oy (YBCO) and YBa2Cu4O8 (Y124) there is no vortex liquid at T=0. This fact allows us to then use measurements of the resistive critical field Hvs(T) to obtain Hc2 in the T=0 limit. By including measurements on the overdoped cuprate Tl2Ba2CuO6+δ (Tl-2201), we establish the full doping dependence of Hc2. The magnitude of Hc2 is found to undergo a sudden drop as the doping is reduced below p=0.18, revealing the presence of a T=0 critical point below which a competing phase markedly weakens superconductivity. This phase is associated with the onset of Fermi-surface reconstruction and charge-density-wave order, generic properties of hole-doped cuprates.
Results
Thermal conductivity
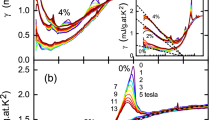
To detect Hc2, we use the fact that electrons are scattered by vortices, and monitor their mobility as they enter the superconducting state by measuring the thermal conductivity κ of a sample as a function of magnetic field H. In Fig. 1, we report our data on YBCO and Y124, as κ vs H up to 45 T, at two temperatures well below Tc (see Methods and Supplementary Note 1). All curves exhibit the same rapid drop below a certain critical field. This is precisely the behaviour expected of a clean type-II superconductor (l0>>ξ0), whereby the long electronic mean free path l0 in the normal state is suddenly curtailed when vortices appear in the sample and scatter the electrons (see Supplementary Note 2). This effect is observed in any clean type-II superconductor, as illustrated in Fig. 1e and Supplementary Fig. 2. Theoretical calculations8 reproduce well the rapid drop of κ at Hc2 (Fig. 1e).
(a–d) Magnetic field dependence of the thermal conductivity κ in YBCO (p=0.11) and Y124 (p=0.14), for temperatures as indicated. The end of the rapid rise marks the end of the vortex state, defining the upper critical field Hc2 (vertical dashed line). In Fig. 1a,c, the data are plotted as κ vs H/Hc2, with Hc2=22 T for YBCO and Hc2=44 T for Y124. The remarkable similarity of the normalized curves demonstrates the good reproducibility across dopings. The large quantum oscillations seen in the YBCO data above Hc2 confirm the long electronic mean path in this sample. In Fig. 1b,d, the overlap of the two isotherms plotted as κ vs H shows that Hc2(T) is independent of temperature in both YBCO and Y124, up to at least 8 K. (e) Thermal conductivity of the type-II superconductor KFe2As2 in the T=0 limit, for a sample in the clean limit (green circles). Error bars represent the uncertainty in extrapolating κ/T to T=0. The data9 are compared with a theoretical calculation for a d-wave superconductor in the clean limit8. (f) Electrical resistivity of Y124 at T=1.5 K (blue) and T=12 K (red) (ref. 11). The green arrow defines the field Hn below which the resistivity deviates from its normal-state behaviour (green dashed line). While Hc2(T) is essentially constant up to 10 K (Fig. 1d), Hvs(T)—the onset of the vortex-solid phase of zero resistance (black arrows)—moves down rapidly with temperature (see also Fig. 3b).
To confirm our interpretation that the drop in κ is due to vortex scattering, we measured a single crystal of Tl-2201 for which l0~ξ0, corresponding to a type-II superconductor in the dirty limit. As seen in Fig. 2a, the suppression of κ upon entering the vortex state is much more gradual than in the ultraclean YBCO. The contrast between Tl-2201 and YBCO mimics the behaviour of the type-II superconductor KFe2As2 as the sample goes from clean (l0~10 ξ0) (ref. 9) to dirty (l0~ξ0) (ref. 10) (see Fig. 2b). We conclude that the onset of the sharp drop in κ with decreasing H in YBCO is a direct measurement of the critical field Hc2, where vortex scattering begins.
(a) Magnetic field dependence of the thermal conductivity κ in Tl-2201, measured at T=6 K on an overdoped sample with Tc=33 K (blue). The data are plotted as κ vs H/Hc2, with Hc2=19 T, and compared with data on YBCO at T=8 K (red; from Fig. 1b), with Hc2=23 T. (b) Corresponding data for KFe2As2, taken on clean9 (red) and dirty10 (blue) samples. (c) Isotherms of κ(H) in Tl-2201, at temperatures as indicated, where κ is normalized to unity at Hc2 (arrows). Hc2 is defined as the field below which κ starts to fall with decreasing field. (d) Temperature dependence of Hc2 (red squares) and Hvs (blue circles) in Tl-2201. Error bars on the Hc2 data represent the uncertainty in locating the onset of the drop in κ vs H relative to the constant normal-state behaviour. All lines are a guide to the eye.
Upper critical field Hc2
The direct observation of Hc2 in a cuprate material is our first main finding. We obtain Hc2=22±2 T at T=1.8 K in YBCO (at p=0.11) and Hc2=44±2 T at T=1.6 K in Y124 (at p=0.14) (Fig. 1a), giving ξ0=3.9 nm and 2.7 nm, respectively. In Y124, the transport mean free path l0 was estimated to be roughly 50 nm (ref. 11), so that the clean-limit condition l0>>ξ0 is indeed satisfied. Note that the specific heat is not sensitive to vortex scattering and so will have a much less pronounced anomaly at Hc2. This is consistent with the high-field specific heat of YBCO at p=0.1 (ref. 5).
We can verify that our measurement of Hc2 in YBCO is consistent with existing thermodynamic and spectroscopic data by computing the condensation energy δE=Hc2/2μ0, where Hc2=Hc1 Hc2/(ln κGL+0.5), with Hc1 the lower critical field and κGL the Ginzburg-Landau parameter (ratio of penetration depth to coherence length). Magnetization data12 on YBCO give Hc1=24±2 mT at Tc=56 K. Using κGL=50 (ref. 12), our value of Hc2=22 T (at Tc=61 K) yields δE/Tc2=13±3 J K−2 m−3. For a d-wave superconductor, δE=NF Δ02/4, where Δ0=α kB Tc is the gap maximum and NF is the density of states at the Fermi energy, related to the electronic specific heat coefficient γN=(2π2/3) NF kB2, so that δE/Tc2=(3α2/8π2) γN. Specific heat data5 on YBCO at Tc=59 K give γN=4.5±0.5 mJ K−2 mol−1 (43±5 J /K−2 m−3) above Hc2. We therefore obtain α=2.8±0.5, in good agreement with estimates from spectroscopic measurements on a variety of hole-doped cuprates, which yield 2Δ0/kBTc~5 between p=0.08 and p=0.24 (ref. 13). This shows that the value of Hc2 measured by thermal conductivity provides quantitatively coherent estimates of the condensation energy and gap magnitude in YBCO.
H—T phase diagram
The position of the rapid drop in κ vs H does not shift appreciably with temperature up to T~10 K or so (Fig. 1b,d), showing that Hc2(T) is essentially flat at low temperature. This is in sharp contrast with the resistive transition at Hvs(T), which moves down rapidly with increasing temperature (Fig. 1f). In Fig. 3, we plot Hc2(T) and Hvs(T) on an H-T diagram, for both YBCO and Y124 (see Methods and Supplementary Methods). In both cases, we see that Hc2=Hvs in the T=0 limit. This is our second main finding: there is no vortex liquid regime at T=0 (see Supplementary Note 3). With increasing temperature the vortex-liquid phase grows rapidly, causing Hvs(T) to fall below Hc2(T). The same behaviour is seen in Tl-2201 (Fig. 2d): at low temperature, Hc2(T) determined from κ is flat, whereas Hvs(T) from resistivity falls abruptly, and Hc2=Hvs at T→0 (see also Supplementary Figs 3 and 4, and Supplementary Note 4).
(a,b) Temperature dependence of Hc2 (red squares, from data as in Fig. 1) for YBCO and Y124, respectively. The red dashed line is a guide to the eye, showing how Hc2(T) might extrapolate to zero at Tc. Error bars on the Hc2 data represent the uncertainty in locating the onset of the downward deviation in κ vs H relative to the normal-state behaviour. The solid lines are a fit of the Hvs(T) data (solid circles) to the theory of vortex-lattice melting1, as in ref. 14. Note that Hc2(T) and Hvs(T) converge at T=0, in both materials, so that measurements of Hvs vs T can be used to determine Hc2(0). In Fig. 3b, we plot the field Hn defined in Fig. 1f (open green squares, from data in ref. 11), which corresponds roughly to the upper boundary of the vortex-liquid phase (see Supplementary Note 3). Error bars on the Hn data represent the uncertainty in locating the onset of the downward deviation in ρ vs H relative to the normal-state behaviour. We see that Hn(T) is consistent with Hc2(T). (c) Temperature TX below which charge order is suppressed by the onset of superconductivity in YBCO at p=0.12, as detected by X-ray diffraction24 (open green circles, from Supplementary Fig. 7). Error bars on the TX data represent the uncertainty in locating the onset of the downward deviation in the x-ray intensity vs T at a given field relative to the data at 17 T (see Supplementary Fig. 7a). We see that TX(H) follows a curve (red dashed line) that is consistent with Hn(T) (at p=0.14; Fig. 3b) and with the Hc2(T) detected by thermal conductivity at lower temperature (at p=0.11 and 0.14). (d) Hvs(T) vs T/Tc, showing a marked increase in Hvs(0) as p goes from 0.12 to 0.18. From these and other data (in Supplementary Fig. 6), we obtain the Hvs(T→0) values that produce the Hc2 vs p curve plotted in Fig. 4a.
H—p phase diagram
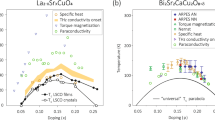
Having established that Hc2=Hvs at T→0 in YBCO, Y124 and Tl-2201, we can determine how Hc2 varies with doping from measurements of Hvs(T) (see Methods and Supplementary Methods), as in Supplementary Figs 5 and 6. For p<0.15, fields lower than 60 T are sufficient to suppress Tc to zero, and thus directly assess Hvs(T→0), yielding Hc2=24±2 T at p=0.12 (Fig. 3c), for example. For p>0.15, however, Tc cannot be suppressed to zero with our maximal available field of 68 T (Fig. 3d and Supplementary Fig. 5), so an extrapolation procedure must be used to extract Hvs(T→0). Following ref. 14, we obtain Hvs(T→0) from a fit to the theory of vortex-lattice melting1, as illustrated in Fig. 3 (and Supplementary Fig. 6). In Fig. 4a, we plot the resulting Hc2 values as a function of doping, listed in Table 1, over a wide doping range from p=0.05 to p=0.26. This brings us to our third main finding: the H—p phase diagram of superconductivity consists of two peaks, located at p1~0.08 and p2~0.18. (A partial plot of Hvs(T→0) vs p was reported earlier on the basis of c-axis resistivity measurements14, in excellent agreement with our own results.) The two-peak structure is also apparent in the usual T—p plane: the single Tc dome at H=0 transforms into two domes when a magnetic field is applied (Fig. 4b).
(a) Upper critical field Hc2 of the cuprate superconductor YBCO as a function of hole concentration (doping) p. Hc2 is defined as Hvs(T→0) (Table 1), the onset of the vortex-solid phase at T→0, where Hvs(T) is obtained from high-field resistivity data (Fig. 3, and Supplementary Figs 5 and 6). The point at p=0.14 (square) is from data on Y124 (Fig. 3b). The points at p>0.22 (diamonds) are from data on Tl-2201 (Table 1, Fig. 2 and Supplementary Fig. 6). Error bars on the Hc2 data represent the uncertainty in extrapolating the Hvs(T) data to T=0. (b) Critical temperature Tc of YBCO as a function of doping p, for three values of the magnetic field H, as indicated (Table 1). Tc is defined as the point of zero resistance. All lines are a guide to the eye. Two peaks are observed in Hc2(p) and in Tc(p; H>0), located at p1~0.08 and p2~0.18 (open diamonds). The first peak coincides with the onset of incommensurate spin modulations at p≈0.08, detected by neutron scattering30 and muon spin spectroscopy31. The second peak coincides with the approximate onset of Fermi-surface reconstruction18,21, attributed to charge modulations detected by high-field NMR (ref. 22) and X-ray scattering23,24,25. (c) Condensation energy δE (red circles), given by the product of Hc2 and Hc1 (see Supplementary Note 5 and Supplementary Fig. 8), plotted as δE/Tc2 vs p. Note the eightfold drop below p2 (vertical dashed line), attributed predominantly to a corresponding drop in the density of states. All lines are a guide to the eye.
Discussion
A natural explanation for two peaks in the Hc2 vs p curve is that each peak is associated with a distinct critical point where some phase transition occurs. An example of this is the heavy-fermion metal CeCu2Si2, where two Tc domes in the temperature-pressure phase diagram were revealed by adding impurities to weaken superconductivity15: one dome straddles an underlying antiferromagnetic transition and the other dome a valence transition16. In YBCO, there is indeed strong evidence of two transitions—one at p1 and another at a critical doping consistent with p2 (ref. 17). In particular, the Fermi surface of YBCO is known to undergo one transformation at p=0.08 and another near p~0.18 (ref. 18). Hints of two critical points have also been found in Bi2Sr2CaCu2O8+δ, as changes in the superconducting gap detected by ARPES at p1~0.08 and p2~0.19 (ref. 19).
The transformation at p2 is a reconstruction of the large hole-like cylinder at high doping that produces a small electron pocket18,20,21. We associate the fall of Tc and the collapse of Hc2 below p2 to that Fermi-surface reconstruction. Recent studies indicate that charge-density wave order plays a role in the reconstruction22,23,24,25. Indeed, the charge modulation seen with X-rays23,24,25 and the Fermi-surface reconstruction seen in the Hall coefficient18,26 emerge in parallel with decreasing temperature (see Fig. 5). Moreover, the charge modulation amplitude drops suddenly below Tc, showing that superconductivity and charge order compete23,24,25 (Supplementary Fig. 7a). As a function of field24, the onset of this competition defines a line in the H—T plane (Supplementary Fig. 7b) that is consistent with our Hc2(T) line (Fig. 3). The flip side of this phase competition is that superconductivity must in turn be suppressed by charge order, consistent with our interpretation of the Tc fall and Hc2 collapse below p2.
Hall coefficient RH(T) of YBCO as a function of temperature at a doping p=0.12 (Tc=66 K), for a field H=15 T (red line, from ref. 26). Tmax is the temperature at which the Hall coefficient RH(T) peaks, before it falls to reach negative values—a signature of Fermi-surface reconstruction18,21. TH is the inflexion point where the downturn in RH(T) begins. The evolution of RH(T) is compared with the growth of charge-density-wave modulations in YBCO detected by X-ray diffraction, at the same doping and field24. As seen, the onset of the modulations, at TCO~130 K, coincides with TH. This suggests a causal connection between charge order and Fermi-surface reconstruction.
We can quantify the impact of phase competition by computing the condensation energy δE at p=p2, using Hc1=110±5 mT at Tc=93 K (ref. 27) and Hc2=140±20 T (Table 1), and comparing with δE at p=0.11 (see above): δE decreases by a factor 20 and δE/Tc2 by a factor 8 (see Supplementary Note 5). In Fig. 4c, we plot the doping dependence of δE/Tc2 (in qualitative agreement with earlier estimates based on specific heat data28—see Supplementary Fig. 8). We attribute the tremendous weakening of superconductivity below p2 to a major drop in the density of states as the large hole-like Fermi surface reconstructs into small pockets. This process is likely to involve both the pseudogap formation and the charge ordering.
Upon crossing below p=0.08, the Fermi surface of YBCO undergoes a second transformation, where the small electron pocket disappears, signalled by pronounced changes in transport properties18,21 and in the effective mass m* (ref. 29). This is strong evidence that the peak in Hc2 at p1~0.08 (Fig. 4a) coincides with an underlying critical point. This critical point is presumably associated with the onset of incommensurate spin modulations detected below p~0.08 by neutron scattering30 and muon spectroscopy31. Note that the increase in m* (ref. 29) may in part explain the increase in Hc2 going from p=0.11 (local minimum) to p=0.08, since Hc2~1/ξ02~1/vF2~m*2.
Our findings shed light on the H-T-p phase diagram of cuprate superconductors, in three different ways. In the H-p plane, they establish the boundary of the superconducting phase and reveal a two-peak structure, the likely fingerprint of two underlying critical points. In the H-T plane, they delineate the separate boundaries of vortex solid and vortex liquid phases, showing that the latter phase vanishes as T→0. In the T-p plane, they elucidate the origin of the dome-like Tc curve as being primarily due to phase competition, rather than fluctuations in the phase of the superconducting order parameter32, and they quantify the impact of that competition on the condensation energy.
Our finding of a collapse in condensation energy due to phase competition is likely to be a generic property of hole-doped cuprates, since Fermi-surface reconstruction—the inferred cause—has been observed in materials such as La1.8-xEu0.2SrxCuO4 (ref. 20) and HgBa2CuO4+δ (refs 33, 34), two cuprates whose structure is significantly different from that of YBCO and Y124. This shows that phase competition is one of the key factors that limit the strength of superconductivity in high-Tc cuprates.
Methods
Samples
Single crystals of YBa2Cu3Oy (YBCO) were obtained by flux growth at UBC (ref. 35). The superconducting transition temperature Tc was determined as the temperature below which the zero-field resistance R=0. The hole doping p is obtained from Tc (ref. 36). To access dopings above p=0.18, Ca substitution was used, at the level of 1.4% (giving p=0.19) and 5% (giving p=0.205). At oxygen content y=6.54, a high degree of ortho-II oxygen order has been achieved, yielding large quantum oscillations37,38, proof of a long electronic mean free path. We used such crystals for our thermal conductivity measurements.
Single crystals of YBa2Cu4O8 (Y124) were grown by a flux method in Y2O3 crucibles and an Ar/O2 mixture at 2,000 bar, with a partial oxygen pressure of 400 bar (ref. 39). Y124 is a stoichiometric underdoped cuprate material, with Tc=80 K. The doping is estimated from the value of Tc, using the same relation as for YBCO (ref. 36). Because of its high intrinsic level of oxygen order, quantum oscillations have also been observed in the highest quality crystals of Y124 (ref. 40). We used such crystals for our thermal conductivity measurements.
Single crystals of Tl2Ba2CuO6 (Tl-2201) were obtained by flux growth at UBC. Compared with YBCO and Y124, crystals of Tl-2201 are in the dirty limit (see Supplementary Note 4). We used such crystals to compare thermal conductivity data in the clean and dirty limits. The thermal conductivity (and resistivity) was measured on two strongly overdoped samples of Tl-2201 with Tc=33 K and 20 K, corresponding to a hole doping p=0.248 and 0.257, respectively. The doping value for Tl-2201 samples was obtained from their Tc, via the standard formula Tc/Tcmax=1–82.6 (p–0.16)2, with Tcmax=90 K.
Resistivity measurements
The in-plane electrical resistivity of YBCO was measured in magnetic fields up to 45 T at the NHMFL in Tallahassee and up to 68 T at the LNCMI in Toulouse. A subset of those data is displayed in Supplementary Fig. 5. From such data, Hvs(T) is determined and extrapolated to T=0 to get Hvs(0), as illustrated in Fig. 3 and Supplementary Fig. 6. The Hc2=Hvs(0) values thus obtained are listed in Table 1 and plotted in Fig. 4a. Corresponding data on Y124 were taken from ref. 11 (see Supplementary Fig. 5). The resistance of a Tl-2201 sample with Tc=59 K (p=0.225) was also measured, at the LNCMI in Toulouse up to 68 T (see Supplementary Figs 5 and 6). In all measurements, the magnetic field was applied along the c axis, normal to the CuO2 planes. (See also Supplementary Methods.)
Thermal conductivity measurements
The thermal conductivity κ of four ortho-II oxygen-ordered samples of YBCO, with p=0.11, was measured at the LNCMI in Grenoble up to 34 T and/or at the NHMFL in Tallahassee up to 45 T, in the temperature range from 1.8 K to 14 K. Data from the four samples were in excellent agreement (see Table 2). The thermal conductivity κ of two single crystals of stoichiometric Y124 (p=0.14) was measured at the NHMFL in Tallahassee up to 45 T, in the temperature range from 1.6 K to 9 K. Data from the two samples were in excellent agreement (see Table 2).
A constant heat current Q was sent in the basal plane of the single crystal, generating a thermal gradient dT across the sample. The thermal conductivity is defined as κ=(Q/dT) (L/w t), where L, w and t are the length (across which dT is measured), width and thickness (along the c axis) of the sample, respectively. The thermal gradient dT=Thot−Tcold was measured with two Cernox thermometers, sensing the temperature at the hot (Thot) and cold (Tcold) ends of the sample, respectively. The Cernox thermometers were calibrated by performing field sweeps at different closely spaced temperatures between 2 K and 15 K. Representative data are shown in Fig. 1. (See also Supplementary Note 1.)
Additional information
How to cite this article: Grissonnanche, G. et al. Direct measurement of the upper critical field in cuprate superconductors. Nat. Commun. 5:3280 doi: 10.1038/ncomms4280 (2014).
References
Blatter, G. et al. Vortices in high-temperature superconductors. Rev. Mod. Phys. 66, 1125–1388 (1994).
Wang, Y. et al. Dependence of upper critical field and pairing strength on doping in cuprates. Science 299, 86–89 (2003).
Senthil, T. & Lee, P. A. Synthesis of the phenomenology of the underdoped cuprates. Phys. Rev. B 79, 245116 (2009).
Li, L. et al. Diamagnetism and Cooper pairing above Tc in cuprates. Phys. Rev. B 81, 054510 (2010).
Riggs, S. C. et al. Heat capacity through the magnetic-field-induced resistive transition in an underdoped high-temperature superconductor. Nat. Phys. 7, 332–335 (2011).
Ando, Y. & Segawa, K. Magnetoresistance of untwinned YBa2Cu3Oy single crystals in a wide range of doping: anomalous hole-doping dependence of the coherence length. Phys. Rev. Lett. 88, 167005 (2002).
Chang, J. et al. Decrease of upper critical field with underdoping in cuprate superconductors. Nat. Phys. 8, 751–756 (2012).
Vorontsov, A. B. & Vekhter, I. Unconventional superconductors under a rotating magnetic field. II. Thermal transport. Phys. Rev. B 75, 224502 (2007).
Reid, J.-Ph. et al. Universal heat conduction in the iron-arsenide superconductor KFe2As2: Evidence of a d-wave state. Phys. Rev. Lett. 109, 087001 (2012).
Dong, J. K. et al. Quantum criticality and nodal superconductivity in the FeAs-based superconductor KFe2As2 . Phys. Rev. Lett. 104, 087005 (2010).
Rourke, P. M. C. et al. Fermi-surface reconstruction and two-carrier modeling of the Hall effect in YBa2Cu4O8 . Phys. Rev. B 82, 020514 (2010).
Liang, R. et al. Lower critical field and superfluid density of highly-underdoped YBa2Cu3O6+x single crystals. Phys. Rev. Lett. 94, 117001 (2005).
Hüfner, S. et al. Two gaps make a high-temperature superconductor? Rep. Prog. Phys. 71, 062501 (2008).
Ramshaw, B. J. et al. Vortex-lattice melting and Hc2 in underdoped YBa2Cu3Oy . Phys. Rev. B 86, 174501 (2012).
Yuan, H. Q. et al. Observation of two distinct superconducting phases in CeCu2Si2 . Science 302, 2104–2107 (2003).
Monthoux, P., Pines, D. & Lonzarich, G. G. Superconductivity without phonons. Nature 450, 1177–1183 (2007).
Tallon, J. L. & Loram, J. W. The doping dependence of T*: What is the real high-Tc phase diagram? Physica C 349, 53–68 (2001).
LeBoeuf, D. et al. Lifshitz critical point in the cuprate superconductor YBa2Cu3Oy from high-field Hall effect measurements. Phys. Rev. B 83, 054506 (2011).
Vishik, I. M. et al. Phase competition in trisected superconducting dome. Proc. Nat. Acad. Sci. 109, 18332–18337 (2012).
Laliberté, F. et al. Fermi-surface reconstruction by stripe order in cuprate superconductors. Nat. Commun. 2, 432 (2011).
Taillefer, L. Fermi surface reconstruction in high-Tc superconductors. J. Phys.: Condens. Matter 21, 164212 (2009).
Wu, T. et al. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3Oy . Nature 477, 191–194 (2011).
Ghiringhelli, G. et al. Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O6+x . Science 337, 821–825 (2012).
Chang, J. et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67 . Nat. Phys. 8, 871–876 (2012).
Achkar, A. J. et al. Distinct charge order in the planes and chains of ortho-III ordered YBa2Cu3Oy by resonant elastic x-ray scattering. Phys. Rev. Lett. 109, 167001 (2012).
LeBoeuf, D. et al. Electron pockets in the Fermi surface of hole-doped high-Tc superconductors. Nature 450, 533–536 (2007).
Liang, R. et al. Lower critical fields in an ellipsoid-shaped YBa2Cu3O6.95 single crystal. Phys. Rev. B 50, 4212–4215 (1994).
Luo, J. L. et al. Doping dependence of condensation energy and upper critical field in YBCO from specific heat measurement. Physica C 341–348, 1837–1840 (2000).
Sebastian, S. E. et al. Metal-insulator quantum critical point beneath the high Tc superconducting dome. Proc. Nat. Acad. Sci. 107, 6175–6179 (2010).
Haug, D. et al. Neutron scattering study of the magnetic phase diagram of underdoped YBa2Cu3O6+x . New J. Phys. 12, 105006 (2010).
Coneri, F. et al. Magnetic states of lightly hole-doped cuprates in the clean limit as seen via zero-field muon spin spectroscopy. Phys. Rev. B 81, 104507 (2010).
Emery, V. J. & Kivelson, S. A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 374, 434–437 (1995).
Doiron-Leyraud, N. et al. Hall, Seebeck, and Nernst coefficients of underdoped HgBa2CuO4+δ: Fermi-surface reconstruction in an archetypal cuprate superconductor. Phys. Rev. X 3, 021019 (2013).
Barisic, N. et al. Universal quantum oscillations in the cuprate superconductors. Nat. Phys. 9, 761–764 (2013).
Liang, R., Bonn, D. A. & Hardy, W. N. Growth of YBCO single crystals by the self-flux technique. Phil. Mag. 92, 2563 (2012).
Liang, R., Bonn, D. A. & Hardy, W. N. Evaluation of CuO2 plane hole doping in YBa2Cu3O6+x single crystals. Phys. Rev. B 73, 180505 (2006).
Doiron-Leyraud, N. et al. Quantum oscillations and the Fermi surface in an underdoped high-Tc superconductor. Nature 447, 565–568 (2007).
Vignolle, B. et al. Coherent c-axis transport in the underdoped cuprate superconductor YBa2Cu3Oy . Phys. Rev. B 85, 224524 (2012).
Adachi, S. et al. Preparation of YBa2Cu4O8 single crystals in Y2O3 crucible using O2-HIP apparatus. Physica C 301, 123–128 (1998).
Bangura, A. F. et al. Small Fermi surface pockets in underdoped cuprate superconductors: Shubnikov-de Haas oscillations in YBa2Cu4O8 . Phys. Rev. Lett. 100, 047004 (2008).
Acknowledgements
We thank Y. Ando, A. Carrington, S.A. Kivelson, A.J. Millis, S. Sachdev and A.-M. Tremblay for fruitful discussions. We thank C. Marcenat for his assistance with the experiments at the LNCMI in Grenoble, and J. Corbin, S. Fortier, and F. Francoeur for their assistance with the experiments at Sherbrooke. R.L., D.A.B. and W.N.H. acknowledge support from NSERC. L.T. acknowledges support from the Canadian Institute for Advanced Research and funding from NSERC, FQRNT, the Canada Foundation for Innovation, and a Canada Research Chair. The work in Toulouse was supported by the French ANR SUPERFIELD, Euromagnet II, and the LABEX NEXT.
Author information
Authors and Affiliations
Contributions
G.G., S.R.d.C. and N.D.-L. performed the thermal conductivity measurements at Sherbrooke. G.G., O.C.-C., S.D.-B., S.K. and N.D.-L. performed the thermal conductivity measurements at the LNCMI in Grenoble. G.G., O.C.-C., A.J.-F., D.G. and N.D.-L. performed the thermal conductivity measurements at the NHMFL in Tallahassee. N.D.-L., D.L., M.S., B.V. and C.P. performed the resistivity measurements at the LNCMI in Toulouse. S.R.d.C., J.C., J.-H.P. and N.D.-L. performed the resistivity measurements at the NHMFL in Tallahassee. M.-È.D., O.C.-C., G.G., F.L., D.L. and N.D.-L. performed the resistivity measurements at Sherbrooke. B.J.R., R.L., D.A.B. and W.N.H. prepared the YBCO and Tl-2201 single crystals at UBC (crystal growth, annealing, de-twinning, contacts). S.A. and N.E.H. prepared the Y124 single crystals. G.G., O.C.-C., F.L., N.D.-L. and L.T. wrote the manuscript. L.T. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-8, Supplementary Notes 1-5, Supplementary Discussion, Supplementary Methods and Supplementary References (PDF 922 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Grissonnanche, G., Cyr-Choinière, O., Laliberté, F. et al. Direct measurement of the upper critical field in cuprate superconductors. Nat Commun 5, 3280 (2014). https://doi.org/10.1038/ncomms4280
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms4280
This article is cited by
-
Planckian dissipation and non-Ginzburg-Landau type upper critical field in Bi2201
Science China Physics, Mechanics & Astronomy (2023)
-
Vinen and Superconductivity: Quantized Vortices
Journal of Low Temperature Physics (2023)
-
Thermodynamic approach for enhancing superconducting critical current performance
NPG Asia Materials (2022)
-
Signatures of a strange metal in a bosonic system
Nature (2022)
-
Little-Parks like oscillations in lightly doped cuprate superconductors
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.