Abstract
High-temperature superconductivity in iron pnictides occurs when electrons and holes are doped into their antiferromagnetic parent compounds. Since spin excitations may be responsible for electron pairing and superconductivity, it is important to determine their electron/hole-doping evolution and connection with superconductivity. Here we use inelastic neutron scattering to show that while electron doping to the antiferromagnetic BaFe2As2 parent compound modifies the low-energy spin excitations and their correlation with superconductivity (<50 meV) without affecting the high-energy spin excitations (>100 meV), hole-doping suppresses the high-energy spin excitations and shifts the magnetic spectral weight to low-energies. In addition, our absolute spin susceptibility measurements for the optimally hole-doped iron pnictide reveal that the change in magnetic exchange energy below and above Tc can account for the superconducting condensation energy. These results suggest that high-Tc superconductivity in iron pnictides is associated with both the presence of high-energy spin excitations and a coupling between low-energy spin excitations and itinerant electrons.
Similar content being viewed by others
Introduction
In conventional Bardeen-Cooper-Schrieffer (BCS) superconductors1, superconductivity occurs when electrons form coherent Cooper pairs below the superconducting transition temperature Tc. Although the kinetic energy of paired electrons increases in the superconducting state relative to the normal state, the reduction in the ion lattice energy is sufficient to give the superconducting condensation energy (Ec=−N(0)Δ2/2 and Δ≈2ħωD , where N(0) is the electron density of states at zero temperature, ħωD is the Debye energy, and V0 is the strength electron-lattice coupling)1,2,3. For iron pnictide superconductors derived from electron or hole-doping of their antiferromagnetic (AF) parent compounds4,5,6,7,8,9, the microscopic origin for superconductivity is unclear. Although spin excitations arising from quasiparticle excitations between the hole pockets near Γ and electron pockets at M in reciprocal space have been suggested as the microscopic origin for superconductivity10,11, orbital fluctuations may also induce superconductivity in these materials12. Here we use inelastic neutron scattering (INS) to systematically map out energy and wave vector dependence of the spin excitations in electron and hole-doped iron pnictides with different superconducting transition temperatures. By comparing the outcome with previous spin wave measurements on the undoped parent compound BaFe2As2 (ref. 13), we find that high-Tc superconductivity only occurs for iron pnictides with low-energy (≤25 meV or ~6.5 kBTc) itinerant electron-spin excitation coupling and high-energy (>100 meV) spin excitations. Since our absolute spin susceptibility measurements for optimally hole-doped iron pnictide reveal that the change in magnetic exchange energy below and above Tc14,15 can account for the superconducting condensation energy, we suggest that the presence of both high-energy spin excitations giving rise to a large magnetic exchange coupling J and low-energy spin excitations coupled to the itinerant electrons are important for high-Tc superconductivity in iron pnictides.
, where N(0) is the electron density of states at zero temperature, ħωD is the Debye energy, and V0 is the strength electron-lattice coupling)1,2,3. For iron pnictide superconductors derived from electron or hole-doping of their antiferromagnetic (AF) parent compounds4,5,6,7,8,9, the microscopic origin for superconductivity is unclear. Although spin excitations arising from quasiparticle excitations between the hole pockets near Γ and electron pockets at M in reciprocal space have been suggested as the microscopic origin for superconductivity10,11, orbital fluctuations may also induce superconductivity in these materials12. Here we use inelastic neutron scattering (INS) to systematically map out energy and wave vector dependence of the spin excitations in electron and hole-doped iron pnictides with different superconducting transition temperatures. By comparing the outcome with previous spin wave measurements on the undoped parent compound BaFe2As2 (ref. 13), we find that high-Tc superconductivity only occurs for iron pnictides with low-energy (≤25 meV or ~6.5 kBTc) itinerant electron-spin excitation coupling and high-energy (>100 meV) spin excitations. Since our absolute spin susceptibility measurements for optimally hole-doped iron pnictide reveal that the change in magnetic exchange energy below and above Tc14,15 can account for the superconducting condensation energy, we suggest that the presence of both high-energy spin excitations giving rise to a large magnetic exchange coupling J and low-energy spin excitations coupled to the itinerant electrons are important for high-Tc superconductivity in iron pnictides.
For BCS superconductors, the superconducting condensation energy Ec and Tc are controlled by the strength of the Debye energy ħωD and electron-lattice coupling V0 (refs 1, 2, 3). A material with large ħωD and lattice exchange coupling is a necessary but not a sufficient condition to have high-Tc superconductivity. On the other hand, a soft metal with small ħωD (such as lead and mercury) will also not exhibit superconductivity with high-Tc. For unconventional superconductors such as iron pnictides, the superconducting phase is derived from hole and electron doping from their AF parent compounds4,5,6,7,8,9. Although the static long-range AF order is gradually suppressed when electrons or holes are doped into the iron pnictide parent compound such as BaFe2As2 (refs 5, 6, 7, 8, 9), short-range spin excitations remain throughout the superconducting phase and are coupled directly with the occurrence of superconductivity16,17,18,19,20,21,22,23,24,25. For spin excitations-mediated superconductors, the superconducting condensation energy should be accounted for by the change in magnetic exchange energy between the normal (N) and superconducting (S) phases at zero temperature. For an isotropic t-J model26, ΔEex(T)=2J[‹Si+x·Si›N−‹Si+x·Si›S], where J is the nearest neighbour magnetic exchange coupling and ‹Si+x·Si› is the dynamic spin susceptibility in absolute units at temperature T14,15. Since the dominant magnetic exchange couplings are isotropic nearest neighbour exchanges for copper oxide superconductors27,28, the magnetic exchange energy ΔEex(T) can be directly estimated using the formula through carefully measuring of J and the dynamic spin susceptibility in absolute units between the normal and superconducting states29,30,31. For heavy Fermion superconductor such as CeCu2Si2, one has to modify the formula to include both the nearest neighbour and next nearest neighbour magnetic exchange couplings appropriate for the tetragonal unit cell of CeCu2Si2 to determine ΔEex(T) (ref. 32). In the case of iron pnictide superconductors5,6,7,8,9, the effective magnetic exchange couplings in their parent compounds are strongly anisotropic along the nearest neighbour ao and bo axis directions of the orthorhombic structure (see inset in Fig. 1a)13,33,34. Although the electron doping induced lattice distortions in iron pnictides35 may affect the effective magnetic exchange couplings36, our INS experiments on optimally electron-doped BaFe1.9Ni0.1As2 indicate that the high-energy spin excitations, which determines the effective magnetic exchange couplings13,33,34, are weakly electron doping-dependent24. Therefore, we can rewrite the relation between the magnetic exchange coupling and the magnetic exchange energy as15
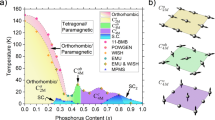
(a) The electronic phase diagram of electron and hole-doped BaFe2As2 (ref. 9). The right inset shows crystal and AF spin structures of BaFe2As2 with marked the nearest (J1a, J1b) and next nearest neighbor (J2) magnetic exchange couplings. The left insets show the evolution of low-energy spin excitations in Ba1−xKxFe2As2. (b,c) Temperature dependence of magnetic susceptibility for our KFe2As2 and Ba0.67K0.33Fe2As2. (d) Temperature dependence of the resistivity for BaFe1.7Ni0.3As2. (e–g) The filled circles are spin excitation dispersions of KFe2As2 at 5 K, Ba0.67K0.33Fe2As2 at 9 K, and BaFe1.7Ni0.3As2 at 5 K, respectively. The shaded areas indicate vanishing spin excitations and the solid lines show spin wave dispersions of BaFe2As2 (ref. 13). (h) Energy dependence of χ″(ω) for BaFe1.9Ni0.1As2 (dashed line), BaFe1.7Ni0.3As2 (green solid circles), Ba0.67K0.33Fe2As2 below (solid red circles and solid red line) and above (open purple circles and solid lines) Tc. The inset shows Energy dependence of χ″(ω) for KFe2As2. The vertical error bars indicate the statistical errors of one standard deviation. The horizontal error bars in (h) indicate the energy integration range.

Here the scattering function S(Q,E=ħω) is related to the imaginary part of the dynamic susceptibility χ″(Q,ω) via S(Q,ω)=[1+n(ω,T)]χ″(Q,ω), where [1+n(ω,T)] is the Bose population factor, Q the wave vector, and E=ħω the excitation energy. J1a is the effective magnetic coupling strength between two nearest sites along the ao direction, while J1b is that along the bo direction and J2 is the coupling between the next nearest neighbour sites (see inset in Fig. 1a)13.
To determine how high-Tc superconductivity in iron pnictides is associated with spin excitations, we consider the phase diagram of electron and hole-doped iron pnictide BaFe2As2 (Fig. 1a)9. In the undoped state, BaFe2As2 forms a metallic low-temperature orthorhombic phase with collinear AF structure as shown in the inset of Fig. 1a. INS measurements have mapped out spin waves throughout the Brillouin zone and determined the effective magnetic exchange couplings13. Upon doping electrons to BaFe2As2 by partially replacing Fe with Ni to induce superconductivity in BaFe2−xNixAs2 with maximum Tc≈20 K at xe=0.1 (ref. 37), the low-energy (<80 meV) spin waves in the parent compounds are broadened and form a neutron spin resonance coupled to superconductivity20,21,22,23, while high-energy spin excitations are weakly affected24. With further electron doping to xe≥0.25, superconductivity is suppressed and the system becomes a paramagnetic metal (Fig. 1a)37. For hole-doped Ba1−xKxFe2As2 (ref. 38), superconductivity with maximum Tc=38.5 K appears at xh≈0.33 (ref. 5) and pure KFe2As2 at xh=1 is a Tc=3.1 K superconductor6. In order to determine how spin excitations throughout the Brillouin zone are correlated with superconductivity in iron pnictides, we study optimally hole-doped Ba0.67K0.33Fe2As2 (Tc=38.5 K, Fig. 1c), pure KFe2As2 (Tc=3 K, Fig. 1b), and nonsuperconducting electron-overdoped BaFe1.7Ni0.3As2 (Fig. 1d). If spin excitations are responsible for mediating electron pairing and superconductivity, the change in magnetic exchange energy between the normal and superconducting state should be large enough to account for the superconducting condensation energy15.
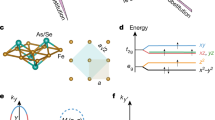
From density functional theory (DFT) calculations, one finds that Fermi surfaces for the undoped parent compound BaFe2As2 consist of hole-like pockets near the Brillouin zone centre and electron pockets near the zone corner (Fig. 2a)10. Figure 2a–d shows the evolution of Fermi surfaces as a function of electron- and hole-doping obtained from the tight-binding model of Graser et al.39 When electrons are doped into the parent compounds, the hole Fermi surfaces decrease in size while the electron pocket sizes increase (Fig. 2b)40. As a consequence, quasiparticle excitations between the hole and electron Fermi surfaces form transversely elongated spin excitations that increase with increasing electron doping23,24,25. For electron-overdoped iron pnictides, the hole pockets sunk below the Fermi surface (Fig. 2c)40. The absence of interband transition between the hole and electron Fermi surfaces is expected to result in a complete suppression of the low-energy spin excitations at the AF ordering wave vector. This is indeed confirmed by nuclear magnetic resonance experiments on electron overdoped Ba(Fe1−xCox)2As2 (ref. 41). For optimally hole-doped iron pnictide Ba0.67K0.33Fe2As2 (inset in Fig. 1a), DFT theory based on sign reversed quasiparticle excitations between hole and electron pockets (Fig. 2d) predicts correctly the longitudinally elongated spin excitations from QAF=(1,0)23,18. In addition, INS work on powder16,17 and single crystals18 of hole-doped Ba1−xKxFe2As2 reveal that the low-energy spin excitations are dominated by a resonance coupled to superconductivity. For pure KFe2As2 (xh=1), low-energy (<14 meV) spin excitations become longitudinally incommensurate from QAF=(1,0) (inset in Fig. 1a)19. These results, as well as the work on electron-doped iron pnictides23,24,25, have shown that the low-energy spin excitations in iron-based superconductors can be accounted for by itinerant electrons on the hole and electron-nested Fermi surfaces9.
Here we use INS to show that the effect of hole-doping to BaFe2As2 is to suppress high-energy spin excitations and transfer the spectral weight to low-energies that couple to the appearance of superconductivity (Fig. 1h). The overall spin excitations spectrum in optimally hole-doped superconducting Ba0.67K0.33Fe2As2 is qualitatively consistent with theoretical methods based on DFT and dynamic mean filed theory (DMFT)42. By using the INS measured magnetic exchange couplings and spin susceptibility in absolute units, we calculate the superconductivity-induced lowering of magnetic exchange energy and find it to be about seven times larger than the superconducting condensation energy determined from specific heat measurements for Ba0.67K0.33Fe2As2 (ref. 43). These results are consistent with spin excitations-mediated electron pairing mechanism15. For the nonsuperconducting electron-overdoped BaFe1.7Ni0.3As2, we find that while the effective magnetic exchange couplings are similar to that of optimally electron-doped BaFe1.9Ni0.1As2 (Fig. 1g)24, the low-energy spin excitations (<50 meV) associated with the hole and electron pocket Fermi surface nesting disappear (Fig. 2c), thus revealing the importance of Fermi surface nesting and itinerant electron-spin excitation coupling to the occurrence of superconductivity (Fig. 1h). Finally, for heavily hole-doped KFe2As2 with low-Tc superconductivity (Fig. 1b), there are only incommensurate spin excitations below ~25 meV possibly due to the mismatched electron-hole Fermi surfaces19,44 and the correlated high-energy spin excitations prevalent in electron-doped and optimally hole-doped iron pnictides are strongly suppressed (Fig. 1e), indicating a dramatic softening of effective magnetic exchange coupling (inset Fig. 1h). Therefore, high-Tc superconductivity is likely associated with two ingredients: a large effective magnetic exchange coupling15, much like the large Debye energy for high-Tc BCS superconductors, and a strong itinerant electrons-spin excitations coupling from the Fermi surface nesting10, similar to electron-phonon coupling in BCS superconductors.
Results
Electron and hole-doping evolution of spin excitations
To substantiate the key conclusions of Fig. 1, we present the two-dimensional (2D) constant-energy images of spin excitations in the (H,K) plane at different energies for KFe2As2 (Fig. 3a–c), Ba0.67K0.33Fe2As2 (Fig. 3d–f), and BaFe1.7Ni0.3As2 (Fig. 3g–i) above Tc. In previous INS work on KFe2As2, longitudinal incommensurate spin excitations were found by triple axis spectrometer measurements for energies from 3 to 14 meV in the normal state19. While we confirmed the earlier work using time-of-flight INS for energies below E=15±1 meV (Fig. 3a,b), our new data collected at higher excitation energies reveal that incommensurate spin excitations converge into a broad spin excitation near E=20 meV and disappear for energies above 25 meV (Fig. 3c; Supplementary Fig. S1). For Ba0.67K0.33Fe2As2, spin excitations at E=5±1 meV are longitudinally elongated from QAF as expected from the DFT calculations (Fig. 3d)18,23. At the resonance energy (E=15±1 meV)16, spin excitations are isotropic above Tc (Fig. 3e). On increasing energy further to E=50±10 meV, spin excitations change to transversely elongated from QAF similar to spin excitations in optimally electron-doped superconductor BaFe1.9Ni0.1As (Fig. 3f)24. Figure 3g–i summarizes similar 2D constant-energy images of spin excitations for nonsuperconducting BaFe1.7Ni0.3As. At E=9±3 (Fig. 3g) and 30±10 meV (Fig. 3h), there are no correlated spin excitations near the QAF. Upon increasing energy to E=59±10 meV (Fig. 3i), we see clear spin excitations transversely elongated from QAF (Fig. 3i; Supplementary Fig. S2). To further illustrate the presence of a large spin gap in BaFe1.7Ni0.3As, we compare spin waves in BaFe2As213 and paramagnetic spin excitations in BaFe1.7Ni0.3As. Figure 4a,b shows the background subtracted spin wave scattering of BaFe2As2 for the Ei=250, 450 meV data, respectively, projected in the wave vector (Q=[1,K]) and energy space at 7 K13. Sharp spin waves are seen to stem from the AF ordering wave vector QAF=(1,0) above the ~15 meV spin gap45. Figure 4c,d shows identical projections for spin excitations of BaFe1.7Ni0.3As at 5 K. A large spin gap of ~50 meV is clearly seen in the data near QAF=(1,0). A detailed comparison of spin excitations in BaFe2−xNixAs2 with xe=0, 0.1, 0.3 is made in Supplementary Figs S3 and S4.
The colour bars represent the vanadium normalized absolute spin excitation intensity in the units of mbarn sr−1 meV−1 f.u.−1. 2D images of spin excitations at 5 K for KFe2As2 (a) E=8±3 meV obtained with Ei=20 meV. The right side incommensurate peak is obscured by background scattering. (b) 13±3 meV with Ei=35 meV, (c) 53±10 meV with Ei=80 meV. For Ba0.67K0.33Fe2As2 at T=45 K, images of spin excitations at (d) E=5±1 meV obtained with Ei=20 meV, (e) 15±1 meV with Ei=35 meV, and (f) 50±2 meV obtained with Ei=80 meV. The dashed box in (d) indicates the AF zone boundaries for a single FeAs layer and the black dashed lines mark the orientations of spin excitations at different energies. Images of spin excitations for BaFe1.7Ni0.3As2 at T=5 K and (g) E=9±3 meV obtained with Ei=80 meV, (h) 30±10 meV with Ei=450 meV, and (i) 59±10 meV with Ei=250 meV. The white crosses indicate the position of QAF.
(a,b) The dispersion cuts of BaFe2As2 with Ei=250 meV and Ei=450 meV along [1,K] direction. The data are from MAPS13. (c,d) Identical dispersion cuts of BaFe1.7Ni0.3As2 (xe=0.3) at MAPS.
Figure 5a–d shows 2D images of spin excitations in BaFe1.7Ni0.3As2 at E=70±10, 112±10, 157±10, and 214±10 meV, respectively. Figure 5e–h shows wave vector dependence of spin excitations at energies E=70±10, 115±10, 155±10 and 195±10 meV, respectively, for Ba0.67K0.33Fe2As2. Similar to spin waves in BaFe2As2 (ref. 13), spin excitations in BaFe1.7Ni0.3As2 and Ba0.67K0.33Fe2As2 split along the K-direction for energies above 80 meV and form rings around Q=(±1,±1) positions near the zone boundary, albeit at slightly different energies. Comparing spin excitations in Fig. 5a–d for BaFe1.7Ni0.3As2 with those in Fig. 5e–h for Ba0.67K0.33Fe2As2 in absolute units, we see that spin excitations in BaFe1.7Ni0.3As2 extend to slightly higher energies and have larger intensity above 100 meV.
Spin excitations of BaFe1.7Ni0.3As2 in the 2D [H,K] plane at energy transfers of (a) E=70±10 meV obtained with Ei=250 meV; (b) 112±10 meV Ei=250 meV; (c) 157±10 meV and (d) 214±10 meV with Ei=450 meV. All obtained at 5 K. A flat backgrounds have been subtracted from the images. Spin excitations of Ba0.67K0.33Fe2As2 at energy transfers of (e) E=70±10 meV obtained with Ei=170 meV; (f) 115±10 meV; (g) 155±10 meV; (h) 195±10 meV obtained with Ei=450 meV, all at 9 K. Wave vector dependent backgrounds have been subtracted from the images. RPA calculations25 of spin excitations for Ba0.67K0.33Fe2As2 at (i) E=70 meV and (j) E=155 meV. DMFT calculations24,42 for Ba0.67K0.33Fe2As2 at (k) E=70 meV and (l) E=155 meV.
As discussed in the spin wave measurements of BaFe2As2 (ref. 13), the magnon band top energy at Q=(1,1) governs the effective magnetic exchange couplings J (J1a, J1b, and J2). To estimate the change of J for hole-doped Ba0.67K0.33Fe2As2, we calculate the energy cut at Q=(1,1) by exploring the Heisenberg Hamiltonian of the parent compound. It turns out that J1a, J1b, and J2 have comparable effect on the band top. On the basis of the dispersion of Ba0.67K0.33Fe2As2, the effective magnetic exchange J is found to be about 10% smaller for Ba0.67K0.33Fe2As2 compared with that of BaFe2As2 (Fig. 6). For comparison, if we assume the band top for KFe2As2 is around E=25 meV, the effective magnetic exchange should be about 90% smaller for KFe2As2. Of course, we know this is not an accurate estimation since spin excitations in KFe2As2 are incommensurate and have an inverse dispersion. In any case, given the zone boundary energy of E≈25 meV (Supplementary Fig. S1), the effective magnetic exchange couplings in KFe2As2 must be much smaller than that of BaFe2As2.
The black line is energy cut at (0.8<H<1.2, 0.8<K<1.2) r.l.u for BaFe2As2 in the Heisenberg spin wave model13. The red line is for Ba0.67K0.33Fe2As2 with 10 % soften band top. The blue line is a similar estimation for KFe2As2 assuming zone boundary is around E=25 meV.
Theoretical calculations of spin excitations
To understand the wave vector dependence of spin excitations in hole-doped Ba0.67K0.33Fe2As2, we have carried out the random phase approximation (RPA) calculation of the dynamic susceptibility in a pure itinerant electron picture using the method described before25. Figure 5i,j shows RPA calculations of spin excitations at E=70 and 155 meV, respectively, for Ba0.67K0.33Fe2As2 assuming that hole doping induces a rigid band shift25. While a pure RPA type itinerant model can explain longitudinally elongated spin excitations at low-energies18, it clearly fails to describe the transversely elongated spin excitations in hole-doped iron pinctides at high energies (Fig. 5e,g). For comparison with the RPA calculation, we also used a combined DFT and DMFT approach24,42 to calculate the imaginary part of the dynamic susceptibility χ″(Q,ω) in the paramagnetic state. Figure 5k,i shows calculated spin excitations at E=70 and 155 meV, respectively. Although the model still does not agree in detail with the data in Fig. 5e,g, it captures the trend of spectral weight transfer away from QAF=(1,0) on increasing energy and forming a pocket centred at Q=(1,1).
Dispersions of spin excitations and local dynamic susceptibility
By carrying out cuts through the 2D images similar to Figs 3d–f and 5e–h along the [1,K] and [H,0] directions (Supplementary Figs S5 and S6), we establish the spin excitation dispersion along the two high symmetry directions for Ba0.67K0.33Fe2As2 and compare with the dispersion of BaFe2As2 (Fig. 1f)13. In contrast to the dispersion of electron-doped BaFe1.9Ni0.1As2 (ref. 24), we find clear softening of the zone boundary spin excitations in hole-doped Ba0.67K0.33Fe2As2 from spin waves in BaFe2As2 (ref. 13). We estimate that the effective magnetic exchange coupling in Ba0.67K0.33Fe2As2 is reduced by about 10% from that of BaFe2As2 (Fig. 6). Similarly, Fig. 1g shows the dispersion curve of BaFe1.7Ni0.3As2 along the [1,K] direction plotted together with that of BaFe2As2 (ref. 13). For energies below ~50 meV, spin excitations are completely gapped marked in the dashed area probably due to the missing hole-electron Fermi pocket quasiparticle excitations40. On the basis of the 2D spin excitation images similar to Fig. 3a–c; we plot in Fig. 1e the dispersion of incommensurate spin excitations in KFe2As2. The incommensurability of spin excitations is weakly energy dependent below E=12 meV but becomes smaller with increasing energy above 12 meV. Correlated spin excitations for energies above 25 meV are suppressed as shown in the shaded area in Fig. 1e.
To quantitatively determine the effect of electron and hole doping on the overall spin excitations spectra, we calculate the local dynamic susceptibility per formula unit (f.u.) in absolute units, defined as χ″(ω)=∫χ″(q,ω)d q/∫d q (ref. 24), where  , at different energies for Ba0.67K0.33Fe2As2, BaFe1.7Ni0.3As2, and KFe2As2. Figure 1h shows the outcome together with previous data on optimally electron-doped superconductor BaFe1.9Ni0.1As2 (ref. 24). While electron doping up to BaFe1.7Ni0.3As2 does not change much the spectral weight of high-energy spin excitations from that of BaFe1.9Ni0.1As2, hole-doping dramatically suppresses the high-energy spin excitations and shift the spectral weight to lower energies (Fig. 1h). For heavily hole-doped KFe2As2, spin excitations are mostly confined to energies below about E=25 meV (inset in Fig. 1h).
, at different energies for Ba0.67K0.33Fe2As2, BaFe1.7Ni0.3As2, and KFe2As2. Figure 1h shows the outcome together with previous data on optimally electron-doped superconductor BaFe1.9Ni0.1As2 (ref. 24). While electron doping up to BaFe1.7Ni0.3As2 does not change much the spectral weight of high-energy spin excitations from that of BaFe1.9Ni0.1As2, hole-doping dramatically suppresses the high-energy spin excitations and shift the spectral weight to lower energies (Fig. 1h). For heavily hole-doped KFe2As2, spin excitations are mostly confined to energies below about E=25 meV (inset in Fig. 1h).
The solid green, red, black, and blue lines in Fig. 7 show calculated local susceptibility in absolute units based on a combined DFT and DMFT approach for KFe2As2, Ba0.67K0.33Fe2As2, BaFe2As2, and BaFe1.9Ni0.1As224, respectively. This theoretical method predicts that electron doping to BaFe2As2 does not affect the spin susceptibility at high energy (E>150 meV), while spin excitations in the hole-doped compound beyond 100 meV are suppressed by shifting the spectral weight to lower energies. This is in qualitative agreement with our absolute intensity measurements (Fig. 1h). The reduction of the high-energy spin spectral weight and its transfer to low energy with hole doping, but not with electron doping, is not naturally explained by the band theory (Fig. 7) and requires models that incorporate both the itinerant quasiparticles and the local moment physics9,42. The hole doping makes the electronic state more correlated, as local moment formation is strongest in the half-filled d5 shell, and mass enhancement larger thereby reducing the electronic energy scale in the problem. The dashed lines in Fig. 7 show the results of calculated local susceptibility using RPA, which clearly fails to describe the electron- and hole-doping dependence of the local susceptibility.
RPA and LDA+DMFT calculations of χ″(ω) in absolute units for KFe2As2 and Ba0.67K0.33Fe2As2 comparing with earlier results for BaFe2As2 and BaFe1.9Ni0.1As224.
Estimation of the superconductivity-induced magnetic exchange energy
Finally, to determine how low-energy spin excitations are coupled to superconductivity in Ba0.67K0.33Fe2As2, we carried out a detailed temperature-dependent study of spin excitation at E=15±1 meV. Comparing with strongly c axis modulated low-energy (E<7 meV) spin excitations18, spin excitations at the resonance energy are essentially 2D without much c axis modulations. In previous work18, we have shown that spin excitations near the neutron spin resonance are longitudinally elongated and change dramatically in intensity across Tc. However, these measurements are obtained in arbitrary units and therefore cannot be used to determine the magnetic exchange energy. Figure 8a–d shows the 2D mapping of the resonance at T=25, 38, 40, and 45 K, respectively. While the resonance reveals a clear oval shape at temperatures below Tc consistent with earlier work (Fig. 8a,b)18, it changes into an isotropic circular shape abruptly at Tc (Fig. 8c,d) as shown by the dashed lines representing full-width-at-half-maximum of the excitations (Supplementary Fig. S7). Temperature dependence of the resonance width along the [H,0] and [1,K] directions in Fig. 8e reveals that the isotropic to anisotropic transition in momentum space occurs at Tc. Figure 8f shows temperature dependence of the resonance from 9–40 K, which vanishes at Tc. Figure 8g plots temperature dependence of the mode energy together with the sum of the superconducting gaps from the hole and electron pockets40. Figure 8h compares temperature dependence of the superconducting condensation energy43 with superconductivity-induced intensity gain of the resonance. By calculating spin excitations induced changes in magnetic exchange energy using equation (1) (see Methods and Supplementary Fig. S8)15, we find that the difference of magnetic exchange interaction energy between the superconducting and normal state is approximately seven times larger than the superconducting condensation energy43, thus indicating that AF spin excitations can be the major driving force for superconductivity in Ba0.67K0.33Fe2As2.
Constant-energy (E=15±1 meV) images of spin excitations at (a) T=25, (b) 38, (c) 40, and (d) 45 K obtained with Ei=35 meV. In order to make fair comparison of the scattering line shape at different temperatures, the peak intensity at each temperature is normalized to 1. The pink and green arrows in (a) mark wave vector cut directions across the resonance. The integration ranges are −0.2≤K≤0.2 along the [H,0] direction and 0.8≤H≤1.2 along the [1,K] direction. The full-width-at-half-maximum (FWHM) of spin excitations are marked as dashed lines. (e) The FWHM of the resonance along the [H,0] and [1,K] directions as a function of temperature across Tc. (f) Energy dependence of the resonance obtained by subtracting the low-temperature data from the 45 K data, and correcting for the Bose population factor. (g) The black diamonds show temperature dependence of the sum of hole and electron pocket electronic gaps obtained from Angle Resolved Photoemission experiments for Ba0.67K0.33Fe2As2 (ref. 40). The red solid circles show temperature dependence of the resonance. (h) Temperature dependence of the superconducting condensation energy from heat capacity measurements43 and the intensity of the resonance integrated from 14–16 meV. The error bars indicate the statistical errors of one s.d.
Discussion
One way to quantitatively estimate the impact of hole/electron doping and superconductivity to spin waves of BaFe2As2 is to determine the energy dependence of the local moment and total fluctuating moments ‹m2› (ref. 24). From Fig. 1h, we see that hole-doping suppresses high-energy spin waves of BaFe2As2 and pushes the spectral weight to resonance at lower energies. The total fluctuating moment of Ba0.67K0.33Fe2As2 below 300 meV is ‹m2›=1.7±0.3 per Fe, somewhat smaller than  per Fe for BaFe2As2 and BaFe1.9Ni0.1As2 (ref. 24). For comparison, BaFe1.7Ni0.3As2 and KFe2As2 have ‹m2›=2.74±0.11 and
per Fe for BaFe2As2 and BaFe1.9Ni0.1As2 (ref. 24). For comparison, BaFe1.7Ni0.3As2 and KFe2As2 have ‹m2›=2.74±0.11 and  per Fe, respectively. Therefore, the total magnetic spectral weights for different iron pnictides have no direct correlation with their superconducting Tcs. Table 1 summarizes the comparison of effective magnetic exchange couplings, total fluctuating moments, and spin excitation band widths for BaFe2−xNixAs2 with xe=0,0.1,0.3 and Ba1−xKxFe2As2 with xh=0.33, 1.
per Fe, respectively. Therefore, the total magnetic spectral weights for different iron pnictides have no direct correlation with their superconducting Tcs. Table 1 summarizes the comparison of effective magnetic exchange couplings, total fluctuating moments, and spin excitation band widths for BaFe2−xNixAs2 with xe=0,0.1,0.3 and Ba1−xKxFe2As2 with xh=0.33, 1.
From Fig. 1h, we also see that the spectral weight of the resonance and low-energy (<100 meV) magnetic scattering in Ba0.67K0.33Fe2As2 is much larger than that of electron-doped BaFe1.9Ni0.1As2. This is consistent with a large superconducting condensation energy in Ba0.67K0.33Fe2As2 since its effective magnetic exchange coupling J is only ~10% smaller than that of BaFe1.9Ni0.1As2 (Fig. 1h)43,46. For electron-overdoped nonsuperconducting BaFe1.7Ni0.3As2, the lack of superconductivity is correlated with the absence of low-energy spin excitations coupled to the hole and electron Fermi surface nesting even though the effective magnetic exchange couplings remain large40,41. This means that by eliminating [‹Si+x· Si›N−‹Si+x· Si›S], there is no magnetic driven superconducting condensation energy, and thus no superconductivity. On the other hand, although the suppression of correlated high-energy spin excitations in KFe2As2 can dramatically reduce the effective magnetic exchange coupling in KFe2As2 (Figs 1e and 6), one can still have superconductivity with reduced Tc. If spin excitations are a common thread of the electron pairing interactions for unconventional superconductors15, our results reveal that the large effective magnetic exchange couplings and itinerant electron-spin excitation interactions may both be important ingredients to achieve high-Tc superconductivity, much like the large Debye energy and the strength of electron-lattice coupling are necessary for high-Tc BCS superconductors. Therefore, our data indicate a possible correlation between the overall magnetic excitation band width, the presence of low-energy spin excitations, and the scale of Tc. This suggests that both high-energy spin excitations and low-energy spin excitation itinerant electron coupling are important for high-Tc superconductivity.
Methods
Sample preparation
Single crystals of Ba0.67K0.33Fe2As2, KFe2As2, and BaFe1.7Ni0.3As2 are grown using the flux method18,25. The actual crystal compositions were determined using the inductively coupled plasma analysis. We coaligned 19 g of single crystals of Ba0.67K0.33Fe2As2 (with in-plane and out-of-plane mosaic of 4°), 3 g of KFe2As2 (with in-plane and out-of-plane mosaic of ~7.5°), and 40 g of BaFe1.7Ni0.3As2 (with in-plane and out-of-plane mosaic of ~3°).
Neutron scattering experiments
Our INS experiments were carried out on the MERLIN and MAPS time-of-flight chopper spectrometers at the Rutherford-Appleton Laboratory, UK13,24. Various incident beam energies were used as specified, and mostly with Ei parallel to the c axis. To facilitate easy comparison with spin waves in BaFe2As2 (ref. 13), we defined the wave vector Q at (qx, qy, qz) as (H,K,L)=(qxao/2π, qybo/2π, qzc/2π) reciprocal lattice units (rlu) using the orthorhombic unit cell, where ao≈bo=5.57 Å, and c=13.135 Å for Ba0.67K0.33Fe2As2, ao≈bo=5.43 Å, and c=13.8 Å for KFe2As2, and ao=bo=5.6 Å, and c=12.96 Å for BaFe1.7Ni0.3As2. The data are normalized to absolute units using a vanadium standard with 20% errors24 and confirmed by acoustic phonon normalization (see Supplementary Note 1). Supplementary Discussion provides additional data analysis on electron-doped iron pnictides, focusing on the comparison of electron overdoped nonsuperconducting BaFe1.3Ni0.3As2 with optimally electron-doped superconductor BaFe1.9Ni0.1As2 and AF BaFe2As2.
DFT+DMFT calculations
Our theoretical DFT+DMFT method for computing the magnetic excitation spectrum employs the ab initio full potential implementation of the method, as detailed in ref. 47. The DFT part is based on the code of Wien2k48. The DMFT method requires solution of the generalized quantum impurity problem, which is here solved by the numerically exact continuous-time quantum Monte Carlo method49,50. The Coulomb interaction matrix for electrons on iron atom was determined by the self-consistent GW method in Kutepov et al.51, giving U=5 eV and J=0.8 eV for the local basis functions within the all electron approach employed in our DFT+DMFT method. The dynamical magnetic susceptibility χ″(Q,E) is computed from the ab initio perspective by solving the Bethe-Salpeter equation, which involves the fully interacting one particle Greens function computed by DFT+DMFT, and the two-particle vertex, also computed within the same method (for details see Park et al.42). We computed the two-particle irreducible vertex functions of the DMFT impurity model, which coincides with the local two-particle irreducible vertex within the DFT+DMFT method. The latter is assumed to be local in the same basis in which the DMFT self-energy is local, here implemented by projection to the muffin-tin sphere.
Calculation of magnetic exchange energy and superconducting condensation energy for Ba0.67K0.33Fe2As2
In a neutron scattering experiment, we measure scattering function S(Q,E=ħω) which is related to the imaginary part of the dynamic susceptibility via S(Q,ω)=[1+n(ω,T)]χ″(Q,ω), where n(ω,T) is the Bose population factor. The magnetic exchange coupling and the imaginary part of spin susceptibility are related via the formula15:

where g=2 is the Landé g-factor. Hence, we are able to obtain the change in magnetic exchange energy between the superconducting and normal states by the experimental data of χ″(Q,ω) in both states using equation (1). Strictly speaking, we want to estimate the zero temperature difference of the magnetic exchange energy between the normal and the superconducting states, and use the outcome to compare with the superconducting condensation energy15. Unfortunately, we do not have direct information on the normal state χ″(Q,ω) at zero temperature. Nevertheless, since our neutron scattering measurements at low-energies showed that the χ″(Q,ω) are very similar below and above Tc near the AF wave vector QAF=(1,0,1) and only a very shallow spin gap at Q=(1,0,0) (see Fig. 1f,h in Zhang et al.18), we assume that there are negligible changes in χ″(Q,ω) above and below Tc at zero temperature for energies below 5 meV. For spin excitation energies above 6 meV, the Bose population factors between 7 and 45 K are negligibly small. In previous work on optimally doped YBa2Cu3O6.95 superconductor, we have assumed that spin excitations in the normal state at zero temperature are negligibly small and thus do not contribute to the exchange energy30.
The directly measured quantity is the scattering differential cross section

where ki and kf are the magnitudes of initial and final neutron momentum and F(Q) is the Fe2+ magnetic form factor, and (γre)2=0.2905, barn·sr−1.
The quantity  χ″(Q,E) in both superconducting and normal states can be fitted by a Gaussian
χ″(Q,E) in both superconducting and normal states can be fitted by a Gaussian  for resonance wave vector (1,0) and by cutting the raw data. The outcome is summarized in the Supplementary Table S1, where the unit of E is meV and that of As(n) is mbarn˙meV−1·sr−1·Fe−1. For the case below 5 meV, we assume that An decreases to zero linearly with energy and As=An (see Fig. 1h in Zhang et al.18), while the σ keeps the value at 5 meV. The assumption is shown in Supplementary Figure S8, where the resonance is seen at E=15 meV.
for resonance wave vector (1,0) and by cutting the raw data. The outcome is summarized in the Supplementary Table S1, where the unit of E is meV and that of As(n) is mbarn˙meV−1·sr−1·Fe−1. For the case below 5 meV, we assume that An decreases to zero linearly with energy and As=An (see Fig. 1h in Zhang et al.18), while the σ keeps the value at 5 meV. The assumption is shown in Supplementary Figure S8, where the resonance is seen at E=15 meV.
Because the condensation energy is only defined at zero temperature, we take T=0 in the formula equation (3) and the integral gives:

The magnetic exchange coupling constants in an anisotropic model are estimated to be

which are 10% smaller than that of BaFe2As2 (ref. 13) and we estimate S to be close to ½ (ref. 24). Hence the exchange energy change is

The condensation energy Uc for optimally doped Ba0.67K0.33Fe2As2 can be calculated to be

from the specific heat data of Popovich et al.43 Therefore, we have the ratio ΔEex/Uc≈7.4, meaning that the change in the magnetic exchange energy is sufficient to account for the superconducting condensation energy in Ba0.67K0.33Fe2As2.
Additional information
How to cite this article: Wang, M. et al. Doping dependence of spin excitations and its correlations with high-temperature superconductivity in iron pnictides. Nat. Commun. 4:2874 doi: 10.1038/ncomms3874 (2013).
References
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of Superconductivity. Phys. Rev. 108, 1175–1204 (1957).
Chester, G. V. Difference between normal and superconducting states of a metal. Phys. Rev. 103, 1693–1699 (1956).
Schrieffer, J. R. Theory of Superconductivity Perseus books (1999).
Kamihara, Y., Watanabe, T., Hirano, M. & Hosono, H. Iron-based layered superconductor La[O1−xFx]FeAs (x=0.05-0.12) with Tc=26 K. J. Am. Chem. Soc. 130, 3296–3297 (2008).
Rotter, M., Tegel, M. & Johrendt, D. Superconductivity at 38 K in the iron arsenide Ba1−xKxFe2As2 . Phys. Rev. Lett. 101, 107006 (2008).
Rotter, M., Pangerl, M., Tegel, M. & Johrendt, D. Superconductivity and crystal structures of (Ba1−xKx)Fe2As2 (x=0−1). Angew. Chem. Int. Ed. 47, 7949–7952 (2008).
de la Cruz, C. et al. Magnetic order close to superconductivity in the iron-based layered LaO1−xFxFeAs systems. Nature 453, 899–902 (2008).
Paglione, J. & Greene, R. L. High-temperature superconductivity in iron-based materials. Nat. Phys. 6, 645–658 (2010).
Dai, P. C., Hu, J. P. & Dagotto, E. Magnetism and its microscopic origin in iron-based high-temperature superconductors. Nat. Phys. 8, 709–718 (2012).
Hirschfeld, P. J., Korshunov, M. M. & Mazin, I. I. Gap symmetry and structure of Fe-based superconductors, Rep. Prog. Phys. 74, 124508 (2011).
Chubukov, A. Pairing mechanism in Fe-based superconductors. Ann. Rev. Condens. Matter Phys. 3, 57–92 (2012).
Kontani, H. & Onari, S. Orbital-fluctuation-mediated superconductivity in iron pnictides: analysis of the five-orbital Hubbard-Holstein model. Phys. Rev. Lett. 104, 157001 (2010).
Harriger, L. W. et al. Nematic spin fluid in the tetragonal phase of BaFe2As2. Phys. Rev. B 84, 054544 (2011).
Scalapino, D. J. & White, S. R. Superconducting condensation energy and an antiferromagnetic exchange-based pairing mechanism. Phys. Rev. B 58, 8222–8224 (1998).
Scalapino, D. J. A common thread: the pairing interaction for the unconventional superconductors. Rev. Mod. Phys. 84, 1383 (2012).
Christianson, A. D. et al. Resonant Spin excitation in the high temperature superconductor Ba0.6K0.4Fe2As2 . Nature 456, 930–932 (2008).
Castellan, J.-P. et al. Effect of Fermi surface nesting on resonant spin excitations in Ba1−xKxFe2As2. Phys. Rev. Lett. 107, 177003 (2011).
Zhang, C. L. et al. Neutron scattering studies of spin excitations in hole-doped Ba0.67K0.33Fe2As2 superconductor. Sci. Rep. 1, 115 (2011).
Lee, C. H. et al. Incommensurate spin fluctuations in hole-overdoped superconductor KFe2As2 . Phys. Rev. Lett. 106, 067003 (2011).
Lumsden, M. D. et al. Two-dimensional resonant magnetic excitation in BaFe1.84Co0.16As2 . Phys. Rev. Lett. 102, 107005 (2009).
Chi, S. et al. Inelastic neutron-scattering measurements of a three-dimensional spin resonance in the FeAs-based BaFe1.9Ni0.1As2 superconductor. Phys. Rev. Lett. 102, 107006 (2009).
Inosov, D. S. et al. Normal-state spin dynamics and temperature-dependent spin-resonance energy in optimally doped BaFe1.85Co0.15As2 . Nat. Phys. 6, 178–181 (2010).
Park, J. T. et al. Symmetry of spin excitation spectra in tetragonal paramagnetic and superconducting phases of 122-ferropnictides. Phys. Rev. B 82, 134503 (2010).
Liu, M. S. et al. Nature of magnetic excitations in superconducting BaFe1.9Ni0.1As2 . Nat. Phys. 8, 376–381 (2012).
Luo, H. Q. et al. Electron doping evolution of the anisotropic spin excitations in BaFe2−xNixAs2 . Phys. Rev. B 86, 024508 (2012).
Spalek, J. t-J model then and now: A personal perspective from the pioneering times. Acta Physica Polonica A 111, 409–424 (2007).
Tranquada, J. M., Xu, G. Y. & Zaliznyak, I. A. Superconductivity, Antiferromagnetism, and Neutron Scattering. J. Magn. Magn. Mater. 350, 148–160 (2014).
Headings, N. S., Hayden, S. M., Coldea, R. & Perring, T. G. Anomalous high-energy spin excitations in the high-Tc superconductor-parent antiferromagnet La2CuO4 . Phys. Rev. Lett. 105, 247001 (2010).
Demler, E. & Zhang, S.-C. Quantitative test of a microscopic mechanism of high-temperature superconductivity. Nature 396, 733–735 (1998).
Woo, H. et al. Magnetic energy change available to superconducting condensation in optimally doped YBa2Cu3O6.95 . Nat. Phys. 2, 600–604 (2006).
Dahm, T. et al. Strength of the spin-fluctuation-mediated pairing interaction in a high-temperature superconductor. Nat. Phys. 5, 217–221 (2009).
Stockert, O. et al. Magnetically driven superconductivity in CeCu2Si2 . Nat. Phys. 7, 119–124 (2011).
Zhao, J. et al. Spin waves and magnetic exchange interactions in CaFe2As2 . Nat. Phys. 5, 555 (2009).
Ewings, R. A. et al. Itinerant spin excitations in SrFe2As2 measured by inelastic neutron scattering. Phys. Rev. B 83, 214519 (2011).
Zhao, J. et al. Structural and magnetic phase diagram of CeFeAsO1−xFx and its relation to high-temperature superconductivity. Nat. Mater. 7, 953–959 (2008).
Yildirim, T. Origin of the 150-K anomaly in LaFeAsO: competing Antiferromagnetic interactions, frustration, and a structural phase transition. Phys. Rev. Lett. 101, 057010 (2008).
Li, L. J. et al. Superconductivity induced by Ni doping in BaFe2As2 single crystals. New J. Phys. 11, 025008 (2009).
Avci, S. et al. Magnetoelastic coupling in the phase diagram of Ba1−xKxFe2As2 as seen via neutron diffraction. Phys. Rev. B 83, 172503 (2011).
Graser, S. et al. Spin fluctuations and superconductivity in a three-dimensional tight-binding model for BaFe2As2. Phys. Rev. B 81, 214503 (2010).
Richard, P., Sato, T., Nakayama, K., Takahashi, T. & Ding, H. Fe-based superconductors: an angle-resolved photoemission spectroscopy perspective. Rep. Prog. Phys. 74, 124512 (2011).
Ning, F. L. et al. Contrasting spin dynamics between underdoped and overdoped Ba(Fe1−xCox)2As2 . Phys. Rev. Lett. 104, 037001 (2010).
Park, H., Haule, K. & Kotliar, G. Magnetic excitation spectra in BaFe2As2: a two-particle approach within a combination of the density functional theory and the dynamical mean-field theory method. Phys. Rev. Lett. 107, 137007 (2011).
Popovich, P. et al. Specific heat measurements of Ba0.68K0.32Fe2As2 single crystals: evidence of a multiband strong-coupling superconducting state. Phys. Rev. Lett. 105, 027003 (2010).
Okazaki, K. et al. Octet-line node structure of superconducting order parameter in KFe2As2 . Science 337, 1314–1317 (2012).
Matan, K., Morinaga, R., Iida, K. & Sato, T. J. Anisotropic itinerant magnetism and spin fluctuations in BaFe2As2: A neutron scattering study. Phys. Rev. B 79, 054526 (2009).
Zeng, B. et al. Specific heat of optimally doped Ba(Fe1−xTM)2As2 (TM= Co and Ni) single crystals at low temperatures: A multiband fitting. Phys. Rev. B 85, 224514 (2012).
Haule, K., Yee, C.-H. & Kim, K. Dynamical mean-field theory within the full-potential methods: Electronic structure of CeIrIn5, CeCoIn5, and CeRhIn5 . Phys. Rev. B 81, 195107 (2010).
Blaha, P., Schwarz, K., Madsen, G. K. H., Kvasnicka, K. & Luitz, J. Wien2K, Karlheinz Schwarz, Technische Universitat Wien, Institut für Physikalische und Theoretische Chemie, Getreidemarkt 9/156, A-1060, Wien/Austria (2001).
Haule, K. Quantum Monte Carlo impurity solver for cluster dynamical mean-field theory and electronic structure calculations with adjustable cluster base. Phys. Rev. B 75, 155113 (2007).
Werner, P., Comanac, A., de' Medici, L., Troyer, M. & Millis, A. J. Continuous-Time Solver for Quantum Impurity Models. Phys. Rev. Lett. 97, 076405 (2006).
Kutepov, A., Haule, K., Savrasov, S. Y. & Kotliar, G. Self-consistent GW determination of the interaction strength: Application to the iron arsenide superconductors. Phys. Rev. B 82, 045105 (2010).
Acknowledgements
The single crystal growth and neutron scattering work at Rice/UTK is supported by the US DOE BES under Grant No. DE-FG02-05ER46202. Work at IOP is supported by the MOST of China 973 programs (2012CB821400, 2011CBA00110) and NSFC. The LDA+DMFT computations were made possible by an Oak Ridge leadership computing facility director discretion allocation to Rutgers. The work at Rutgers is supported by DOE BES DE-FG02-99ER45761 (G.K.) and NSF-DMR 0746395 (K.H.). T.A.M. acknowledges the Center for Nanophase Materials Sciences, which is sponsored at ORNL by the Scientific User Facilities Division, BES, US DOE.
Author information
Authors and Affiliations
Contributions
This paper contains data from three different neutron scattering experiments in the group of P.D. lead by M.W. (Ba0.67K0.33Fe2As2), C.Z. (KFe2As2), and X.L. (BaFe1.7Ni0.3As2). These authors made equal contributions to the results reported in the paper. For Ba0.67K0.33Fe2As2, M.W., H.L., E.A.G. and P.D. carried out neutron scattering experiments. Data analysis was done by M.W. with help from H.L. and E.A.G. The samples were grown by C.Z., M.W., Y.S., X.L. and coaligned by M.W. and H.L. RPA calculation is carried out by T.A.M. The DFT and DMFT calculations were done by Z.Y., K.H. and G.K. Superconducting condensation energy was estimated by X.Z. For KFe2As2, the samples were grown by C.Z and G.T. Neutron scattering experiments were carried out by C.Z., E.A.G. and P.D. For BaFe1.7Ni0.3As2, the samples were grown by X.L., H.L., and coaligned by. X.Y.L. and M.Y.W. Neutron scattering experiments were carried out by X.L., T.G.P. and P.D. The data are analysed by X.L. The paper was written by P.D., M.W., X.L. and C.L.Z. with input from T.M., K.H. and G.K. All co-authors provided comments on the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S9, Supplementary Tables S1-S2, Supplementary Note 1 and Supplementary Discussion (PDF 2402 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Wang, M., Zhang, C., Lu, X. et al. Doping dependence of spin excitations and its correlations with high-temperature superconductivity in iron pnictides. Nat Commun 4, 2874 (2013). https://doi.org/10.1038/ncomms3874
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms3874
This article is cited by
-
Iron pnictides and chalcogenides: a new paradigm for superconductivity
Nature (2022)
-
Spin-excitation anisotropy in the nematic state of detwinned FeSe
Nature Physics (2022)
-
Epitaxial integration of a perpendicularly magnetized ferrimagnetic metal on a ferroelectric oxide for electric-field control
Rare Metals (2022)
-
High-energy magnetic excitations from heavy quasiparticles in CeCu2Si2
npj Quantum Materials (2021)
-
Resonance from antiferromagnetic spin fluctuations for superconductivity in UTe2
Nature (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.