Abstract
Crackling noise is a common feature in many systems that are pushed slowly, the most familiar instance of which is the sound made by a sheet of paper when crumpled. In percolation and regular aggregation, clusters of any size merge until a giant component dominates the entire system. Here we establish ‘fractional percolation’, in which the coalescence of clusters that substantially differ in size is systematically suppressed. We identify and study percolation models that exhibit multiple jumps in the order parameter where the position and magnitude of the jumps are randomly distributed—characteristic of crackling noise. This enables us to express crackling noise as a result of the simple concept of fractional percolation. In particular, the framework allows us to link percolation with phenomena exhibiting non-self-averaging and power law fluctuations such as Barkhausen noise in ferromagnets.
Similar content being viewed by others
Introduction
Many systems crackle when pushed slowly. Examples include the crumpling of paper1, earthquakes2, solar flares3, the dynamics of superconductors4 and the magnetization of slowly magnetized magnets. For a piece of wood in fire one can even hear crackling noise without special equipment. Across all systems that display crackling noise, the order parameter of the system exhibits randomly distributed jumps, and discrete, spontaneous events span a broad range of sizes5. Magnification of the hysteresis curve of a magnetic material in a changing external field, for instance, reveals that the magnetization curve is not smooth but exhibits small discontinuities. This series of correlated jumps is called the Barkhausen effect, which is a standard example for crackling noise in physics6,7,8. Despite its importance, crackling noise is far from being understood.
In random network percolation a fixed number of nodes are chosen randomly, and two of them are connected according to certain rules9,10,11,12. This procedure is repeated over and over again until every node is connected to every other. Once the number of added links exceeds a certain critical value, extensively large connected components (clusters) emerge that dominate the system.
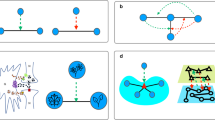
The reverse process is called fragmentation, see Fig. 1. Fragmentation processes, where homogeneous parts break up into smaller ones, are ubiquitous and have been studied intensely. The applications range from disintegration of atomic nuclei, and the fragmentation of glass rods, to fracture in large-scale systems13,14,15,16,17,18,19. An important observation is that the size of the fragments are of the same order of magnitude as the parent pieces. Thus, the case where one fragment is microscopic while the size of the other fragment is substantially larger is rare.
(a) In the process of fragmentation, clusters split up into parts of a certain fraction. (b) The reverse dynamics, ‘fractional percolation’, is studied here. In contrast to ordinary aggregation processes, in fractional percolation the coalescence of clusters that substantially differ in size is systematically suppressed.
Here we model this by systematically suppressing asymmetric break ups. This suppression suggests a fractional increase of clusters, that is time-reversed fragmentation. We demonstrate that crackling noise in percolation unexpectedly emerges from this simple fractional growth rule. To further demonstrate the universality of our approach, computer simulations for the proposed percolation mechanism in geometrical confinement are carried out.
The particular model we use to exemplify the fractional growth mechanism can be replaced by any other model where first a fixed number of nodes are chosen at random, and then two nodes are connected, according to any rule that forbids the largest chosen component to merge with components smaller than a fixed fraction of its size. As we will reveal by a single event analysis, the network model features three basic properties: (i) a fractional growth mechanism, (ii) a threshold mechanism and (iii) a mechanism that amplifies critical fluctuations. We show that these underlying mechanisms account for the main features of crackling noise. Perhaps most importantly, the framework allows us to derive macroscopic features from the underlying micro-dynamical mechanisms, which exposes connections between the seemingly unrelated concepts of percolation, fragmentation and crackling noise.
Results
Network model
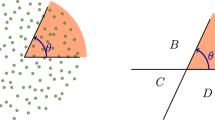
Consider a network with a fixed number of nodes N and L links. Start with N isolated nodes and no links, L=0. At each step, choose three different nodes v1, v2 and v3 uniformly at random. Let S1, S2 and S3 denote the sizes of the (not necessarily distinct) clusters they reside in. Assume S1≥S2≥S3, and 0<f≤1 is fixed. Connect those two nodes vi and vj for which Δij:=fSi−Sj, 1≤i<j≤3 is minimal, see Fig. 2. If necessary, choose randomly among multiple minima, whose corresponding nodes are to be linked. Hence, a certain type of size homophily among clusters is applied, where connections between two clusters are preferred, which are similar in size, after the size of the larger cluster has been rescaled by a factor f, the ‘target fraction’. As Δ12≤Δ13, only Δ12 and Δ23 have to be considered. The rule is also applied if the nodes to be linked reside in the same component. As a ‘final rule’, when there are only two clusters left in the system, connect these. For single realizations of the process, see Fig. 3. As seen in the study, fragmentation as S→(gS:=Si, (1−g)S:=Sj) with  is the inverse process, and the target fraction f determines the magnitude of the discontinuities in the order parameter.
is the inverse process, and the target fraction f determines the magnitude of the discontinuities in the order parameter.
(a) Select three nodes at random and calculate the sizes of the clusters they reside in S1≥S2≥S3. Connect those two nodes νi and νj, which reside in clusters that minimize Δij:=fSi−Sj among Δ12, Δ13 and Δ23, where 0<f≤1 is fixed. (Actually, it is unnecessary to consider Δ13 as Δ12≤Δ13). Here a link between the clusters of size 15 and 10 is established because the (arbitrarily chosen) fixed target fraction f=2/3 is here exactly met: Δ12=2/3 × 15−10=0<Δ23=2/3 × 10−5=5/3<Δ13=2/3 × 15−5=5. (b) Lattice model. Draw randomly a focal cluster (red) and merge those two neighbour clusters that minimize Δ (see text).
(a) Scheme of crackling noise in network percolation. Single realizations of fractional percolation processes for the network size N=218. The evolution of the largest component S1/N is displayed. The control parameter f determines the magnitude of the discontinuities. In the thermodynamic limit N→∞, the process shows infinitely many discontinuous jumps. (b) Same for the magnetization of the Barkhausen model on a square lattice, N=400 × 400, single realization for f=0.01.
Let us order the largest components of the system by S1, S2, …, with sizes s1=S1/N≥s2=S2/N…, and write ‘with high probability’ (whp) to express that the probability of a certain statement gets arbitrarily close to 1 as N→∞. The link density of the network is the analogue of the occupation probability for lattices and defined by p=L/N, where L denotes the number of links that have been added to the network. Let pc characterize the critical link density, the position of the (first) phase transition.
We show next that an arbitrarily fractional increase of components features discontinuities that survive even in the thermodynamic limit, and that this implies non-self-averaging15.
Self-averaging
A thermodynamic quantity, such as the total magnetization or the size of the largest component in a networked system s1, is self-averaging if its relative variance becomes zero in the thermodynamic limit15,

where the brackets denote ensemble averaging.
For non-self-averaging systems, however, the thermodynamic quantity remains broadly distributed for large systems and large sample sizes. Systems that lack self-averaging therefore lack the collapse of the ensemble average, and its minimum and maximum as well. Non-self-averaging has an important role in the statistical physics of disordered systems, for instance in spin glasses15,20,21, neural networks, polymers and population biology22,23.
We characterize non-self-averaging in percolation24,25 by a non-vanishing relative variance of the order parameter s1 on an extended interval. For investigating this, it is helpful to study the underlying microscopic mechanisms in terms of a single event analysis.
Fractional growth mechanism
First we show that, for f>0, the largest component cannot merge with components smaller than  . If less than three distinct clusters are picked, either an intracluster link is added and the size of largest component is necessarily unchanged, or the size of the largest component doubles. Thus, we consider the case of three distinctly chosen components whose sizes are ordered,
. If less than three distinct clusters are picked, either an intracluster link is added and the size of largest component is necessarily unchanged, or the size of the largest component doubles. Thus, we consider the case of three distinctly chosen components whose sizes are ordered,  ≥
≥ ≥
≥ .
.
Proof by contradiction: Assume Δ1,2 is minimal such that  and
and  merge when (A)
merge when (A)  . In fact, Δ1,3 is never minimal (except if it is equal to another Δ) as Δ1,3≥Δ1,2, and if Δ2,3 was minimal then the largest chosen cluster would not merge with any other. By multiplying A with f and adding −
. In fact, Δ1,3 is never minimal (except if it is equal to another Δ) as Δ1,3≥Δ1,2, and if Δ2,3 was minimal then the largest chosen cluster would not merge with any other. By multiplying A with f and adding − we obtain
we obtain  . As Δ1,2 is minimal, we have f
. As Δ1,2 is minimal, we have f −
− <f
<f −
− , and hence we obtain f
, and hence we obtain f , which is impossible for f>0.
, which is impossible for f>0.
Thus,  either stays constant, increases ‘fractionally’ by at least a factor of
either stays constant, increases ‘fractionally’ by at least a factor of  or is overtaken (by a merger of
or is overtaken (by a merger of  and
and  ). However, overtaking becomes unlikely as the size of the largest component increases.
). However, overtaking becomes unlikely as the size of the largest component increases.
Impossibility of  (N) overtaking
(N) overtaking
By 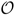 (N) overtaking, we mean the merger of two components, each smaller than the largest component, which together are larger than the largest component and of size
(N) overtaking, we mean the merger of two components, each smaller than the largest component, which together are larger than the largest component and of size 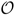 (N). Our line of arguments holds for any rule based on picking at most three nodes randomly. Assume that S1 =
(N). Our line of arguments holds for any rule based on picking at most three nodes randomly. Assume that S1 = 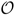 (N), considering the following cases.
(N), considering the following cases.
Case (i): Both smaller components are 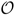 (N). This is (whp) impossible because the upper limit for the number of macroscopic components is 2. Actually for any n-node rule (where first n nodes are chosen randomly followed by any other rule), there cannot exist more than n−1 macroscopic clusters over any extended period of time26.
(N). This is (whp) impossible because the upper limit for the number of macroscopic components is 2. Actually for any n-node rule (where first n nodes are chosen randomly followed by any other rule), there cannot exist more than n−1 macroscopic clusters over any extended period of time26.
Case (ii): At least one of the smaller components is o(N). In this case, overtaking is (whp) impossible as either S1≥S2′+S3′ or S1→S1+o(N).
Threshold mechanism
Taken together, for the infinite system, this implies that as soon as the size of the second largest component exceeds  , the second largest component merges with the largest one, s1→s1+s2. As a third macroscopic component is (whp) impossible, this also implies the reset of the second largest component, s2→0.
, the second largest component merges with the largest one, s1→s1+s2. As a third macroscopic component is (whp) impossible, this also implies the reset of the second largest component, s2→0.
Power law fluctuations by amplification of critical fluctuations
Summarizing the above considerations, after the first-phase transition, for p>pc and N→∞, the size of the largest component either stays constant or jumps discontinuously. As the first transition is point-continuous24,27,28, the process necessarily exhibits infinitely many discontinuous transitions arbitrarily close to the first transition point, p=pc.
Let δn denote the height of the nth step down the staircase. The fractional growth mechanism suggests the proportionality δn~gn, where  . This yields the jump size distribution
. This yields the jump size distribution

for f>0, where δ(·) denotes the Delta function and γ is a constant. This is supported by numerics (see Fig. 4).
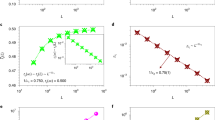
The relative variance  of the largest component in dependence on the link density p is displayed, f=1. For p>pc the system is non-self-averaging characterized by
of the largest component in dependence on the link density p is displayed, f=1. For p>pc the system is non-self-averaging characterized by  →const.>0, for N→∞. Upper inset: Stochasticity of transition points characterized by the lack of the collapse of average, minimum and maximum values of S1, here shown for f=1 and an ensemble of 500 realizations. A single realization is displayed in black. Lower inset: As derived in the text, for any f>0, N→∞, the jump sizes are power law distributed, D(s)~s−τ (τ=1 theory). Fit exponents τf=1=0.96±0.06 (R=0.990), τf=0.5=0.85±0.03 (R=0.998) and τf=0.1=0.90±0.04 (R=0.997). Error bars indicate standard deviations.
→const.>0, for N→∞. Upper inset: Stochasticity of transition points characterized by the lack of the collapse of average, minimum and maximum values of S1, here shown for f=1 and an ensemble of 500 realizations. A single realization is displayed in black. Lower inset: As derived in the text, for any f>0, N→∞, the jump sizes are power law distributed, D(s)~s−τ (τ=1 theory). Fit exponents τf=1=0.96±0.06 (R=0.990), τf=0.5=0.85±0.03 (R=0.998) and τf=0.1=0.90±0.04 (R=0.997). Error bars indicate standard deviations.
The stochasticity is a consequence of the exponential amplification of the critical fluctuations of s1 at the first-phase transition point, pc. Fluctuations, measured by the relative variance, in the size of the largest component s1 at pc are known to be non-zero,  (s1(pc))>0 (refs 9, 27).
(s1(pc))>0 (refs 9, 27).
From δn≈εgn, we see that uncertainties ε are exponentially suppressed as n increases. In contrast, fluctuations in s1 at pc are exponentially amplified, for increasing p. As a result, both the size of the jumps, and the transition points are stochastic—even for the infinite system.
Thus, the process is non-self-averaging, characterized by a non-vanishing relative variance

This is numerically supported, see Fig. 4, and stands in contrast to the weakly discontinuous case (see Supplementary Methods and Supplementary Figs S1–S3).
Expressing δn in terms of a time-dependent target fraction f(n), and assuming f(n)=α/n, 0<α≤1, from equation (2), we obtain D(s)~ characterizing power law fluctuations that decay faster than ~s−1. Thus, other fluctuation types than ~s−1 are accessible via a non-constant f.
characterizing power law fluctuations that decay faster than ~s−1. Thus, other fluctuation types than ~s−1 are accessible via a non-constant f.
Barkhausen percolation model
As clusters in our framework neither have a magnetization nor are geometrically confined, the analogy to magnetic effects such as the Barkhausen effect, a standard example of crackling noise in geometrical confinement, remains incomplete. To demonstrate the universality of our claims, next we study a Barkhausen percolation model on a square lattice. Assume that each cluster has a homogeneous magnetization; either m(Si)=0 or m(Si)=1. Initially all sites are single clusters and have m=0, up to a set of sites of o(N) that is set to m=1, for example, a few single clusters. Now apply repeatedly the following update rule. (i) Uniformly draw a cluster at random, (ii) among this focal cluster and its (von Neumann-) neighbours, merge those two neighbour clusters that minimize Δ:=fSi−Sj (see Fig. 2b), (iii) magnetization: apply the neutral rules 0+0→0, and 1+1→1, together with the magnetization rule 0+1→1, for the merging clusters. In addition, apply the physical time increment rule t→t+min(si, sj)1/2 at each merger, si and sj being the scaled cluster sizes of two merging components. This rule accounts for cracks preceding a fragmentation. Cracks have a finite propagation velocity, which implies that duration of a fragmentation event depends on the size of the fragments15,29. Here we have arbitrarily chosen the square root of the smaller cluster as the time increment. However, the main features of the model are independent of the specific choice.
Fragmentation mimics the repeated reconfiguration of homogeneous magnetic domains under a slowly increased opposite external magnetic field. A magnetic domain is a region within a ferromagnetic material with uniform magnetization. During the demagnetization, domains split up into smaller ones of different magnetization, a process called reconfiguration. This is in most ferromagnetic materials the dominating factor in the minimization of the local magnetostatic energy and accounts for the sudden jumps of the total magnetization in the hysteresis curve. However, due to other effects, the process stops when the domain size approaches a threshold, usually in range of 10−4 to 10−6 m (refs 5, 8).
Here we demonstrate that the reverse process, fractional percolation, reproduces the main features of Barkhausen noise. While only a caricature of the intricate processes in ferromagnets6,7, it nonetheless explains multiple randomly distributed discontinuous jumps in the total magnetization  , together with non-SA, and power law fluctuations, see Fig. 5, Supplementary Methods and Supplementary Figs S4–S7.
, together with non-SA, and power law fluctuations, see Fig. 5, Supplementary Methods and Supplementary Figs S4–S7.
Power law fluctuations (a) in the largest cluster size, and (b) in the total magnetization. The jump size distributions D(s)~s−τ suggest a power law decay. Lattice size N=500 × 500 (periodic boundary conditions). Initial condition with a single magnetized cluster. Jumps smaller than the relative size 7 × 10−4 are discarded. Data points are averaged over 1,000 realizations, using logarithmic binning. Distributions without using log-bins are shown in Supplementary Fig. S6. Error bars indicate standard deviations. (a) Fit exponents τf=0.01=1.7±0.2 (R=0.983), τf=0.25=1.4±0.03 (R=0.999) and τf=1=1.4±0.04 (R=0.999). (b) Fit exponents τf=0.01=1.8±0.02 (R=0.999), τf=0.25=1.6±0.07 (R=1.00) and τf=1=1.4±0.01 (R=1.00).
Discussion
We have established crackling noise in percolation. In particular, we have demonstrated analytically that fractional growth rules imply randomly distributed jumps in the order parameter. These jumps are discontinuous phase transitions. However, when such mechanisms are mixed, even weakly, with mechanisms that merge components purely at random then the transitions vanish, or become at most weakly discontinuous characterized by very small power law exponents30,31,32,33,34,35,36,37,38,39,40,41, see Supplementary Methods and Supplementary Figs S1–S3.
Fractional percolation describes nucleation where domains cannot grow in arbitrarily small pace. As an application consider an unmagnetized ferromagnetic sample of linear dimension of about l=1 cm at room temperature. It is not unrealistic to assume that the magnetic domains have roughly the same linear dimension l0=10−3 cm, independent of l, but different magnetizations that globally compensate each other. An increasing external magnetic field typically causes magnetic domains to increase at least by the size of one of its neighbour domains. Thus, this mechanism alone would result in the total magnetization to either stay constant or jump in steps of the size of magnetic domains. As long as l0>0, this quantized growth is an example of the fractional growth rule as the largest domain cannot increase by arbitrarily small amounts. However, as we increase the sample size, the ratio l0/l decreases such that for the infinite system any jump size becomes zero relative to the system size. Thus our framework suggests that Barkhausen noise is at most ‘weakly discontinuous’. In fact, in many soft magnetic materials Barkhausen jump sizes are not extensive and thus their relative size shrinks with increasing system size8. In contrast, in thin magnetic films and other geometries where long-range interactions are not of major importance, macroscopic jumps have been reported42.
The characteristics of fractional percolation are robust against an arbitrary (time-dependent) variation of the parameter f>0 that determines the magnitude of the discontinuities. The framework combines mechanisms reminiscent of many physical and biological systems: the order parameter exhibits a sudden jump upon exceeding a dynamical threshold5,29,43,44, and large-scale fluctuations emerge as a consequence of critical fluctuations. The amplification and propagation of critical fluctuations to macroscopic scales has been subject of intensive investigations in quantum critical systems, such as the inflationary expansion of the early universe45, and disordered systems exhibiting quenched disorder20,21. However, the current understanding of most systems where randomness is frozen or amplified is far from being complete. A recent study on group formation in small growing populations, for instance, shows that the fraction of one trait within the population (for example, cooperators) can be subject to strong fluctuations as a result of the amplification of stochastic fluctuations generated during the initial phase of the dynamics46,47.
Power law fluctuations across operating scales, discontinuous jumps of the order parameter and non-self-averaging may considerably subvert predictability and control of networked systems11,48. Exact conditions for these phenomena are elusive15. Our analysis provides sufficient conditions for these features. Because the framework connects the seemingly unrelated concepts of percolation, fragmentation and crackling noise, it might help to qualitatively improve the understanding of systems that display (stochastic) discontinuous phase transitions.
In short, we expressed the main features of crackling noise as a consequence of a simple concept: fractional percolation.
Methods
Mixed model
For a general argument, we introduce a stochastic mix of two processes, ordinary Erdös-Renyí (ER) percolation, and the simple model of fractional percolation introduced in the main text. Consider a graph G(ν, ε), where the vertex set ν has N nodes, and the edge set ε has L links. Start with N isolated nodes and an empty set of edges  . With probability q, connect two randomly chosen different nodes (that is, ER rule), otherwise, at each step, choose three different nodes v1, v2 and v3 uniformly from V (for fractional percolation) and follow the steps given in the main text (choose the minimal Δ), see Supplementary Fig. S1.
. With probability q, connect two randomly chosen different nodes (that is, ER rule), otherwise, at each step, choose three different nodes v1, v2 and v3 uniformly from V (for fractional percolation) and follow the steps given in the main text (choose the minimal Δ), see Supplementary Fig. S1.
Global continuity for q>0
Consider any rule based on picking a fixed number of nodes randomly, which is applied, at each step with probability 1−q, such as fractional percolation, or other types of discontinuous percolation, together with an ER-type process, which is applied with probability q, such as ER percolation. Here, by ER-type process, we mean a percolation process, based on randomly choosing a fixed number of nodes, which does not allow the emergence of more than a single giant component because it would instantaneously merge with any other macroscopic component of size 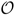 (N). After the first-phase transition, that is, for p>pc a giant component necessarily must have emerged. Hence, for fixed q>0 and N→∞ there is no extended interval (pc,p*>pc) in which macroscopic components smaller than the largest one can emerge, because the ER-type rule would merge them infinitely often with the largest one in any extended subinterval. This cannot be compensated even by high rates of the creation of components of size
(N). After the first-phase transition, that is, for p>pc a giant component necessarily must have emerged. Hence, for fixed q>0 and N→∞ there is no extended interval (pc,p*>pc) in which macroscopic components smaller than the largest one can emerge, because the ER-type rule would merge them infinitely often with the largest one in any extended subinterval. This cannot be compensated even by high rates of the creation of components of size 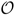 (N), because at any given time there exist at most 1/α components of size αN, or greater for α>0. As a result, for p>pc all components smaller than the largest one are at any time of o(N), and discontinuous jumps in s1 are therefore impossible. Clearly, for p<pc all components S1, S2,… are microscopic, that is of size o(N). As any rule based on randomly picking a fixed number of nodes is necessarily point-continuous at the first transition point p=pc (refs 24, 25), the order parameter s1, the size of largest cluster, is globally continuous and we can state that, for q >0, the process is globally continuous.
(N), because at any given time there exist at most 1/α components of size αN, or greater for α>0. As a result, for p>pc all components smaller than the largest one are at any time of o(N), and discontinuous jumps in s1 are therefore impossible. Clearly, for p<pc all components S1, S2,… are microscopic, that is of size o(N). As any rule based on randomly picking a fixed number of nodes is necessarily point-continuous at the first transition point p=pc (refs 24, 25), the order parameter s1, the size of largest cluster, is globally continuous and we can state that, for q >0, the process is globally continuous.
Barkhausen percolation model
The size of the largest cluster necessarily displays a stochastic staircase on an extended interval after tc, where tc is the first-phase transition point, for N→∞. Large randomly distributed jumps of the total magnetization are a consequence of this.
For the Barkhausen model on a square lattice (introduced in main text), numerical evidence is presented that the total magnetization exhibits discontinuous jumps, and displays power law fluctuations together with non-self-averaging.
Single realizations of the Barkhausen model are shown in Supplementary Fig. S4. In contrast to the self-averaging case shown in Supplementary Fig. S3,Fig. S5 indicates that the relative variance of M (and S1) is non-zero on a finite interval and does not shrink to a single peak for N→∞.
In addition, Supplementary Fig. S6 provides numerical evidence for large-scale fluctuations, for all values of the parameter f. In ordinary square lattice percolation, the critical window (around the phase-transition point tc) is characterized by fluctuations that decay as D(s)~s−τ, with τ≈2.0. For the thermodynamical limit, the exponent is exactly known, τ=187/91 (ref. 9). For small values of f, an exponent close to τ=1.7 is observed here.
In contrast, we find larger fluctuations exhibiting a decay closer to a power law with exponent 3/2, for f=0.25, and f=1. We expect this fluctuation type for finite systems with a sufficiently high tendency for the suppression of the growth of large clusters—in stark contrast to ordinary percolation. More precisely, the assumption that the cluster sizes develop similarly to percolation in 1d, or equivalently, to the ‘global competition model’ studied in Nagler et al.31, leads to the prediction  , where T is the (unscaled) time, that is the number of added links or bonds, and n and T are connected via the identity
, where T is the (unscaled) time, that is the number of added links or bonds, and n and T are connected via the identity  (ref. 31). Finite size fluctuations in the critical window are then expected to follow
(ref. 31). Finite size fluctuations in the critical window are then expected to follow  , where the prime indicates the derivative. Hence,
, where the prime indicates the derivative. Hence,  , for some constant γ>0. This result is in agreement with the numerical results shown in Supplementary Fig. S6, for not too small values of f.
, for some constant γ>0. This result is in agreement with the numerical results shown in Supplementary Fig. S6, for not too small values of f.
In contrast, this behaviour is expected to vanish in the limit N→∞. In this limit, fractional percolation on a lattice is expected to exhibit D(s)~s−1, as a consequence of the stochastic staircase on a finite interval (see main text).
However, the studied system sizes do not allow to observe this behaviour with statistical significance, as the size of the critical window is too large for the studied system sizes, implying D(s)~s−3/2. Nevertheless, the statistics of large fluctuations of the magnetization for f=1 is not inconsistent with D(s)~s−1. For the lattice model, the fact that the stochastic staircase is extended after tc is a result of the physical time increment rule t→t+min(si, sj) (introduced in the main text). This particular rule accounts for the finiteness of the crack propagation velocity.
(introduced in the main text). This particular rule accounts for the finiteness of the crack propagation velocity.
Importantly, for t>tc any other size-dependent delay also leads to (i) discontinuous transitions that are (ii) randomly distributed (non-self-averaging) together with (iii) large-scale fluctuations.
In agreement with the framework, for the studied system sizes, we numerically find the largest gap in M (and S1) to be effectively independent of the system size, see Supplementary Fig. S7.
Therefore we have demonstrated strong numerical evidence that the Barkhausen process involves macroscopic broadly distributed jumps in the total magnetization, together with non-self-averaging.
Additional information
How to cite this article: Schröder, M. et al. Crackling noise in fractional percolation. Nat. Commun. 4:2222 doi: 10.1038/ncomms3222 (2013).
References
Houle, P. A. & Sethna, J. P. Acoustic emission from crumpling paper. Phys. Rev. E 54, 278–283 (1996).
Gutenberg, B. & Richter, C. F. Seismicity of the Earth and Associated Phenomena Princeton Univ. Press (1954).
Lu, E. T., Hamilton, R. J., McTiernan, J. M. & Bromond, K. R. Solar flares and avalanches in driven dissipative systems. Astrophys. J. 412, 841–852 (1993).
Field, S., Witt, J., Nori, F. & Ling, X. Superconducting vortex avalanches. Phys. Rev. Lett. 74, 1206–1209 (1995).
Sethna, J. P., Dahmen, K. A. & Myers, C. R. Crackling noise. Nature 410, 242–250 (2001).
Zapperi, S. et al. Signature of effective mass in crackling-noise asymmetry. Nat. Phys. 1, 46–49 (2005).
Papanikolaou, S. et al. Universality beyond power laws and the average avalanche shape. Nat. Phys. 7, 316–320 (2011).
Jiles, D. Introduction to Magnetism and Magnetic Materials Chapman & Hall (1998).
Stauffer, D. & Aharony, A. Introduction to Percolation Theory 2nd edn Taylor & Francis (2003).
Sahimi, M. Applications of Percolation Theory Taylor & Francis (1994).
Parshani, R., Buldyrev, S. V., Stanley, H. E. & Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 464, 1025–1028 (2010).
Spencer, J. The giant component: The golden anniversary. Am. Math. Soc. 57, 720–724 (2010).
Redner, S. Statistical Models for the Fracture of Disordered Media (eds Herrmann H. J., Roux S. Elsevier Science (1990).
Krapivsky, P. L., Grosse, I. & Ben-Naim, E. Scale invariance and lack of self-averaging in fragmentation. Phys. Rev. E(R) 61, R993–R996 (2000).
Sornette, D. Critical Phenomena in Natural Sciences, Chaos, Fractals, Self-organization and Disorder: Concepts and Tools Springer Series in Synergetics (2004).
Sornette, D., Vanneste, C. & Knopoff, L. Statistical model of earthquake foreshocks. Phys. Rev. A 45, 8351–8357 (1992).
Ishii, T. & Matsushita, M. Fragmentation of long thin glass rods. J. Phys. Soc. Jpn 61, 3474–3477 (1992).
Oddershede, L., Dimon, P. & Bohr, J. Self-organized criticality in fragmenting. Phys. Rev. Lett. 71, 3107–3110 (1993).
Kadono, T. Fragment mass distribution of platelike objects. Phys. Rev. Lett. 78, 1444–1447 (1997).
Sherrington, D. & Kirkpatrick, S. Solvable model of a spin-glass. Phys. Rev. Lett. 32, 1792–1796 (1975).
Kirkpatrick, S. & Sherrington, D. Infinite-ranged models of spin-glasses. Phys. Rev. B 17, 4384–4403 (1978).
Mézard, M., Parisi, G. & Virasoro, M. A. Spin Glass Theory and Beyond World Scientific (1988).
Derrida, B. Random-energy model: An exactly solvable model of disordered systems. Phys. Rev. B 24, 2613–2626 (1981).
Riordan, O. & Warnke, L. Explosive Percolation is Continuous. Science 333, 322–324 (2011).
Riordan, O. & Warnke, L. Achlioptas processes are not always self-averaging. Phys. Rev. E 86, 011129 (2012).
Nagler, J., Tiessen, T. & Gutch, H. W. Continuous percolation with discontinuities. Phys. Rev. X 2, 031009 (2012).
Aharony, A. & Harris, A. B. Absence of self-averaging and universal fluctuations in random systems near critical points. Phys. Rev. Lett. 77, 3700–3703 (1996).
Riordan, O. & Warnke, L. Explosive percolation is continuous. Ann. Appl. Probab. 22, 1450–1464 (2012).
Sornette, D. & Vanneste, C. Dynamics and memory effects in rupture of thermal fuse networks. Phys. Rev. Lett. 68, 612–615 (1992).
Achlioptas, D., D'Souza, R. M. & Spencer, J. Explosive percolation in random networks. Science 323, 1453–1455 (2009).
Nagler, J., Levina, A. & Timme, M. Impact of single links in competitive percolation. Nat. Phys. 7, 265–270 (2011).
Chen, W. & D’Souza, R. M. Explosive percolation with multiple giant components. Phys. Rev. Lett. 106, 115701 (2011).
D'Souza, R. M. Complex networks: Structure comes to random graphs. Nat. Phys. 5, 627 (2009).
da Costa, R. A., Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Explosive percolation transition is actually continuous. Phys. Rev. Lett. 105, 255701 (2010).
Grassberger, P., Christensen, C., Bizhani, G., Son, S.-W. & Paczuski, M. Explosive percolation is continuous, but with unusual finite size behavior. Phys. Rev. Lett. 106, 225701 (2011).
Radicchi, F. & Fortunato, S. Explosive percolation in scale-free networks. Phys. Rev. Lett. 103, 168701 (2009).
Araújo, N. A. M. & Herrmann, H. J. Explosive percolation via control of the largest cluster. Phys. Rev. Lett. 105, 035701 (2010).
Friedman, E. J. & Landsberg, A. S. Construction and analysis of random networks with explosive percolation. Phys. Rev. Lett. 103, 255701 (2009).
Ziff, R. M. Explosive growth in biased dynamic percolation on two-dimensional regular lattice networks. Phys. Rev. Lett. 103, 045701 (2009).
Schrenk, K. J. et al. Bohman-Frieze-Wormald model on the lattice, yielding a discontinuous percolation transition. Phys. Rev. E 85, 031103 (2012).
D'Souza, R. M. & Mitzenmacher, M. Local cluster aggregation models of explosive percolation. Phys. Rev. Lett. 104, 195702 (2010).
Berger, A. et al. Disorder-driven hysteresis-loop criticality in Co/CoO films. J. Appl. Phys 89, 7466–7468 (2001).
Bak, P., Tang, C. & Wiesenfeld, K. Self-organized criticality: an explanation for 1/f noise. Phys. Rev. Lett. 59, 381–384 (1987).
Bak, P., Tang, C. & Wiesenfeld, K. Self-organized criticality. Phys. Rev. A 38, 364–374 (1988).
Peebles, P. J. E. The Large Scale Structure of the Universe Princeton University Press (1980).
Melbinger, A., Cremer, J. & Frey, E. Evolutionary game theory in growing populations. Phys. Rev. Lett. 105, 178101 (2010).
Cremer, J., Melbinger, A. & Frey, E. Growth dynamics and the evolution of cooperation in microbial populations. Sci. Rep 2, 281 (2012).
Liu, Y., Slotine, J.-J. & Barabasi, A.-L. Controllability of complex networks. Nature 473, 167–173 (2011).
Acknowledgements
We cordially thank E. Vives, P. Grassberger, M.P. Touzel, and A. Trabesinger for valuable comments. S.H.E.R. is supported by grant no. 90004064 from INSF.
Author information
Authors and Affiliations
Contributions
J.N. conceived the idea. M.S. and J.N. contributed in designing the research. M.S., J.N. and S.H.E.R. analysed the data. M.S. performed the network simulations. S.H.E.R. performed the lattice simulations. M.S. and J.N. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S7 (PDF 975 kb)
Rights and permissions
About this article
Cite this article
Schröder, M., Rahbari, S. & Nagler, J. Crackling noise in fractional percolation. Nat Commun 4, 2222 (2013). https://doi.org/10.1038/ncomms3222
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms3222
This article is cited by
-
Crackling noise microscopy
Nature Communications (2023)
-
Universal gap scaling in percolation
Nature Physics (2020)
-
Failure and recovery in dynamical networks
Scientific Reports (2017)
-
Universality in boundary domain growth by sudden bridging
Scientific Reports (2016)
-
Anomalous critical and supercritical phenomena in explosive percolation
Nature Physics (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.