Abstract
Spin ice is a magnetic analog of H2O ice that harbors dense static disorder. Dipolar interactions between classical spins yield a frozen frustrated state with residual configurational Pauling entropy and emergent magnetic monopolar quasiparticles. Introducing quantum fluctuations is of great interest as this could melt spin ice and allow coherent propagation of monopoles. Here, we report experimental evidence for quantum dynamics of magnetic monopolar quasiparticles in a new class of spin ice based on exchange interactions, Pr2Zr2O7. Narrow pinch point features in otherwise diffuse elastic neutron scattering reflects adherence to a divergence-free constraint for disordered spins on long time scales. Magnetic susceptibility and specific heat data correspondingly show exponentially activated behaviors. In sharp contrast to conventional ice, however, >90% of the neutron scattering is inelastic and devoid of pinch points furnishing evidence for magnetic monopolar quantum fluctuations.
Similar content being viewed by others
Introduction
Classical Ising spins with dipolar interactions on the pyrochlore lattice possess a macroscopically degenerate ensemble of ground states1,2. Satisfying the two-in two-out ice rule on each tetrahedron3,4, these states of rare-earth spins in magnets such as Dy2Ti2O7 and Ho2Ti2O7 are in one-to-one correspondence with the disordered configurations of protons in H2O ice (Fig. 1a). Mimicking the formation of an H3O+–OH− electric dipole in water ice, a spin flip from the spin ice manifold fractionalizes into a pair of emergent magnetic monopolar quasiparticles with Coulomb attraction5,6,7,8,9.
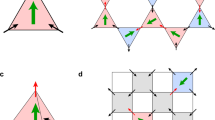
(a,b,c) A fragment of the pyrochlore structure is shown to illustrate the 2-in 2-out ice rule for the configuration of proton (blue sphere) and oxygen (red sphere) sites in water ice (a), classical Ising spins (green arrows) with dipolar interaction in spin ice (b), and the D3d crystal electric field doublet ground state wave function in exchange spin ice with superexchange interactions mediated by oxygen 2p orbitals at the center of each tetrahedron (c). The signs of the 4f and 2p wave functions are denoted by red and blue colors. The light yellow belt indicates a superexchange path. (d) Real part of the AC-susceptibility (χ′). Inset: DC field divided by magnetization H/M(T) for temperatures from 10 K to 2 K and μ0H=0.1 T. (e) Imaginary part of the AC-susceptibility (χ′′). Inset: measurement frequency versus inverse freezing temperature defined as the peak temperature for χ′′(T). The solid line denotes a fit to the Arrhenius law, which yields an activation energy Δχ=1.62(3) K. (f) Magnetic and nuclear part of the specific heat CMN for Pr2Zr2O7 after subtracting lattice and CEF contributions in zero field (open blue circle) (see Supplementary Note 4 for details). A refined estimate CM=CMN−CN (filled blue circle) was obtained by subtracting a scaled nuclear Schottky-like anomaly (solid blue line). CM for Dy2Ti2O7, adapted from ref. 2, is also shown for comparison (filled green square). Inset: CM versus 1/T on a semi-logarithmic scale. The solid line denotes a fit to an Arrhenius law between 2 to 0.2 K, which yields an activation energy of 0.72(1) K. (g) Magnetic entropy ΔSM (filled blue circle) for Pr2Zr2O7 calculated from CM. Open green squares show ΔSM for Dy2Ti2O7 (ref. 2). The dashed black lines denote the entropy for a two level system ( ) and the spin ice entropy defined as the difference between
) and the spin ice entropy defined as the difference between  and the Pauling entropy of
and the Pauling entropy of  =0.292
=0.292 .
.
In classical spin ice, monopole dynamics is diffusive—only activated thermally or by external magnetic field5,6,10 as solitons in semiclassical spin chains11. The classical nature of Ising spins precludes attainment of thermal equilibrium at temperatures (T) below the effective nearest neighbor energy scale Jff. Quantum fluctuations enhance dynamics and might allow coherent propagation of magnetic charge12,13,14,15, much as spinons in one-dimensional quantum magnets16.
Contrary to H2O ice, pyrochlore-based rare-earth spin systems17 provide excellent opportunities to explore quantum effects in ice. Quantum fluctuations were theoretically proposed as the origin of a putative spin liquid in Tb2Ti2O7 (ref. 18). More recently, experimental work on Pr2Ir2O7 shows the possibility of a chiral spin liquid phase when quantum fluctuations melt spin ice19,20. Strong spin fluctuations were observed for Pr2Sn2O7 (ref. 21) and Yb2Ti2O7 (refs 22, 23, 24, 25), which have spin ice correlations. There, superexchange interactions for the smaller moment Pr3+ and Yb3+ systems are much stronger than dipolar interactions; so, the materials are referred to as exchange(-based) spin ice (Fig. 1c)24,26. In this class of spin ice, the two-in two-out states should no longer be static, but dynamic—described by a quantum superposition of the spin ice manifold. Here, we report the experimental observation of spin ice correlations and quantum dynamics in Pr2Zr2O7.
Results
Magnetic properties
Thermomagnetic measurements on Pr2Zr2O7 provide key insights particularly when compared with the classical spin ice compounds (Fig. 1). We have succeeded in growing high-quality single crystals, which are stoichiometric to the 1–2% level, as determined by chemical analyses and single crystal synchrotron X-ray diffraction measurements (Supplementary Figures S1 and S2, Supplementary Tables S1 and S2, and Supplementary Note 1). The temperature-dependence of the inverse susceptibility of single crystalline Pr2Zr2O7 exhibits Curie–Weiss behavior for T <10 K with an effective moment μeff=2.5(1)μB (Fig. 1d, inset) that is four times smaller than for dipolar spin ice Dy2Ti2O7 where μeff=10μB. Correspondingly, Pr2Zr2O7 displays an antiferromagnetic Weiss temperature ΘW=−1.4(1) K compared with the ferromagnetic ΘW ≈ +0.5 K for dipolar Dy2Ti2O7 (ref. 2).
While no anomaly indicating long-range ordering was found down to 20 mK, AC-χ(T) exhibits a frequency-dependent peak at T0(f), which is the onset temperature for dynamics at the frequency, f (Fig. 1d). The data for T0(f) (Fig. 1e, inset) are consistent with thermal activation over at least three decades. For classical spin ice, the corresponding activation energy Δχ=1.62(3) K, is the spin flip energy, 2Jff, from the ice manifold. Though the activation energies are similar, the limiting (attempt) frequency f0~1 MHz for Pr2Zr2O7 is three orders of magnitude larger than for Dy2Ti2O7 (refs 10, 27). Moreover, upon cooling to the lowest T, the real part of AC-χ(T) approaches 50% of the peak height while it vanishes for Dy2Ti2O7 (refs 27, 28). These indicators of enhanced fluctuations at low temperatures are consistent with general expectations for a quantum spin system.
Crystal electric field
To determine the crystal electric field (CEF) scheme, we used inelastic neutron scattering and found five magnetic excitations at energy transfers 9.5 meV, 57.1 meV, 81.9 meV, 93.2 meV and 109 meV (Fig. 2). Simultaneous fitting of a crystal field model to neutron and magnetic susceptibility data (Fig. 2) shows the ground state is a magnetic doublet with (111) Ising anisotropy, as in classical spin ice systems1 (Supplementary Tables S3, S4, and Supplementary Note 2). This is, however, not a Kramers doublet; so, although the specific heat data (Fig. 1f) show there is no conventional Jahn-Teller transition, magneto-elastic effects may have an important role in Pr2Zr2O7.
Main panel: magnetic excitation spectrum obtained by combining T=7.8 K data for two incident beam energies: Ei=40 meV and Ei=120 meV. The blue dashed line denotes fitted polynomial backgrounds. The red solid line is the calculated best fit. Inset: temperature dependence of the inverse magnetic susceptibility. The red solid line in the inset was calculated using the same crystal field parameters as used to account for the neutron scattering data (Supplementary Tables S3 and S4). Details are provided in the Supplementary Note 2.
Elastic and inelastic neutron scattering
Low-energy transfer neutron-scattering data provide a direct view of dynamics in the spin ice state. A 40 mm × 20 mm2 cylindrical single crystal was used to achieve sufficient magnetic scattering intensity from the relatively small Pr3+ moments. Nominally elastic magnetic scattering covering broad regions of momentum space develops upon cooling from 22 K to 0.1 K, indicating short-range quasi-static spin correlations (Fig. 3b). Sharp pinch point features near (111) and particularly (002), bear evidence of a divergence-free two-in two-out spin configuration on each tetrahedron9,25,29,30. Indeed, the elastic Q-map resembles a classical Monte Carlo simulation for an exchange-only model9,29, which indicates dominant ferromagnetic superexchange interactions in Pr2Zr2O7. ΘW is, however, negative and this suggests—consistent with recent theoretical predictions31,32—the exchange Hamiltonian includes antiferromagnetic transverse terms that induce quantum dynamics. Though the ground state doublet is Jahn–Teller active, the observed scattering does not resemble that predicted for a model where the local three fold axis is broken30.
(a) Inelastic Q-map with energy transfer of 0.25 meV obtained after subtracting the corresponding data at 15 K as background. The broad diffuse scattering pattern carries the symmetry of the crystal but cannot be associated with phonon scattering, which is concentrated around strong nuclear Bragg peaks at low energies. Instead we associate it with inelastic magnetic scattering. The fact that the scattering is wave vector dependent further links it to inter-site quantum spin dynamics. (b) Elastic Q-map with pinch points at (002), (111), and ( ). By subtracting 22 K data from 0.1 K data to cancel elastic nuclear scattering processes at Bragg peaks, we obtain quasi-static spin correlations on the time scale of τ=/δE=2 ps. The black ellipses at (002) in (a) and (b) indicate the full width at half maximum instrumental resolution. (c) Temperature-dependence of the spin ice correlation length ξice (left) and the relaxation rate Γ (right). The black solid line denotes
). By subtracting 22 K data from 0.1 K data to cancel elastic nuclear scattering processes at Bragg peaks, we obtain quasi-static spin correlations on the time scale of τ=/δE=2 ps. The black ellipses at (002) in (a) and (b) indicate the full width at half maximum instrumental resolution. (c) Temperature-dependence of the spin ice correlation length ξice (left) and the relaxation rate Γ (right). The black solid line denotes  with the activation energy fixed at the value of Δχ=1.62(3) K. The red solid line shows
with the activation energy fixed at the value of Δχ=1.62(3) K. The red solid line shows  , where C=1.4(2). The black horizontal dashed line indicates the mean distance between 1% of the Pr sites, which according to synchrotron X-ray analysis are occupied by Zr (Supplementary Figure S2 and Supplementary Note 1). (d) Inelastic neutron scattering (INS) spectra at Q=(003) and T=0.1 K (solid circle) and 2.0 K (open circle) after subtraction of INS data obtained at the same Q but at the elevated temperature of 15 K. A correction to the monitor rate was applied to account for order contamination in the unfiltered incident beam. The fitting curve and the corresponding background resulting from subtraction of magnetic scattering at T=15 K to derive Γ are shown by red solid and blue dashed curves, respectively. The details of the analysis are described in Supplementary Note 3. The error bars reflect one s.d. counting statistics. When error bars are not visible they are smaller than the symbol size.
, where C=1.4(2). The black horizontal dashed line indicates the mean distance between 1% of the Pr sites, which according to synchrotron X-ray analysis are occupied by Zr (Supplementary Figure S2 and Supplementary Note 1). (d) Inelastic neutron scattering (INS) spectra at Q=(003) and T=0.1 K (solid circle) and 2.0 K (open circle) after subtraction of INS data obtained at the same Q but at the elevated temperature of 15 K. A correction to the monitor rate was applied to account for order contamination in the unfiltered incident beam. The fitting curve and the corresponding background resulting from subtraction of magnetic scattering at T=15 K to derive Γ are shown by red solid and blue dashed curves, respectively. The details of the analysis are described in Supplementary Note 3. The error bars reflect one s.d. counting statistics. When error bars are not visible they are smaller than the symbol size.
The transverse width of the pinch points in elastic neutron scattering is a measure of the density of Pr tetrahedra that violate the ice rule7, hence the monopole density. To determine this density, we measured the pattern of elastic magnetic neutron scattering near the Q=(002) pinch point with a high-resolution configuration. Two configurations of the MACS instrument were used for this experiment. For rapid high statistical mapping of Q-dependent scattering, we used a fixed final neutron energy Ef=5 meV. The corresponding measured energy resolution δE=0.38 meV and the calculated principal axes of the Q resolution near (002) are δQ1=0.093 Å−1 and δQ2=0.041 Å−1. For high-resolution measurements, we used Ef=2.7 meV, where δE=0.12 meV, δQ1=0.093 Å−1, δQ2=0.025 Å−1, and the incoherent elastic count rate is reduced by a factor 5. The pinch point width was extracted by fitting the following phenomenological model of scattering to two-dimensional intensity maps in the (HHL) reciprocal lattice plane7,9 (see Supplementary Note 3 for details):

Both the quasi-static (τ>/δE=6 ps) total moment S(0), and the spin ice correlation length ξice increase on cooling (Fig. 3c and Supplementary Figure S3). The low T limit, ξ0, indicates a quasi-static monopole density of 1.2%. This can be compared with the ~1% concentration of Zr on Pr sites determined by single crystal synchrotron X-ray diffraction (Supplementary Figure S2 and Supplementary Note 1). The fitting function,  , (black solid line, Fig. 3c) describes the data well with the activation energy fixed at the value of Δχ=1.6 K extracted from AC-χ(T) data (Fig. 1e, inset).
, (black solid line, Fig. 3c) describes the data well with the activation energy fixed at the value of Δχ=1.6 K extracted from AC-χ(T) data (Fig. 1e, inset).
The wave vector map of inelastic scattering at ω=0.25 meV and T=0.1 K is shown in Fig. 3a. As ħω>>kBT~0.01 meV, the inelastic scattering is evidence for quantum spin dynamics and the frequency scale of ν=ω/2π=60 GHz sets it apart from the thermally activated spin dynamics probed by AC susceptibility measurements on the kHz frequency scale. While the overall pattern resembles the nominally elastic scattering (Fig. 3b), the pinch points have vanished. Excited states thus differ from the ground state by the appearance of tetrahedra that violate the ice rule or in other words by the presence of magnetic monopoles. Combined, the elastic scattering that does show pinch points and the inelastic scattering that does not, constitute experimental evidence for magnetic monopoles with quantum dynamics. By normalizing the intensity data (Supplementary Note 3 and Supplementary Figure S3), we find that such inelastic scattering accounts for >90% of the magnetic scattering cross section of the low-energy CEF doublet at T=0.1 K. This shows magnetism in Pr2Zr2O7 is dominated by quantum fluctuations.
To characterize the monopole fluctuation spectrum, we carried out constant Q=(003) scans at various Ts, subtracting T=15 K data as a background (Fig. 3d). The low T spectrum places an upper limit of ΔE=0.2 meV on any excitation gap. Upon heating the spectrum broadens and to quantify this effect, we fitted the T-difference data to the scattering associated with a single imaginary pole response, χ(ω)=χ0Γ/(Γ−iω), accounting for the background subtraction with a consistent T=15 K relaxation rate as detailed in Supplementary Note 3. Figure 3c shows the T-dependence of the relaxation rate, Γ. At high temperatures, Γ might be interpreted as a monopole relaxation rate. The red solid line shows  , where C=1.4(2). The crossover to linearity and thus ω/T scaling is evidence of a regime for T>Jff, where T is the only relevant energy scale. In the low T limit, Γ~0.17 meV is similar to the spin flip energy 2Jff=Δχ~1.6 K inferred from AC-χ(T). The observation of a broad spectrum rather than a sharp spin flip mode indicates monopole quantum dynamics12,14,15. A possible low-energy regime of photons predicted for a U(1) spin liquid12,14,15, however, cannot be resolved in the present neutron scattering experiment.
, where C=1.4(2). The crossover to linearity and thus ω/T scaling is evidence of a regime for T>Jff, where T is the only relevant energy scale. In the low T limit, Γ~0.17 meV is similar to the spin flip energy 2Jff=Δχ~1.6 K inferred from AC-χ(T). The observation of a broad spectrum rather than a sharp spin flip mode indicates monopole quantum dynamics12,14,15. A possible low-energy regime of photons predicted for a U(1) spin liquid12,14,15, however, cannot be resolved in the present neutron scattering experiment.
Heat capacity
Complementary information about the excitation spectrum is provided by specific heat measurements (Fig. 1f) (see Supplementary Note 4 for details). After subtraction of the lattice and CEF contributions, the temperature-dependence of the magnetic and nuclear-specific heat CMN(T) does not exhibit sharp features that would result from long-range ordering or a conventional Jahn–Teller transition. Instead, a broad peak at T~2 K ~Δχ=2Jff~1.6 K (Fig. 1f) can be associated with the proliferation of thermally activated monopole pairs. While the position of the peak is similar to that for Dy2Ti2O7, the greater width is consistent with the broad spectrum of inelastic neutron scattering and monopole quantum dynamics in Pr2Zr2O7.
The upturn in CMN(T) below ~200 mK provides valuable information about electronic dynamics on the nuclear spin time scale. A fully frozen state of ~3.0 μB Pr moments would generate a nuclear Schottky peak at ~0.17 K with a height of ~7 J mol−1 K−1, which is inconsistent with the data. Instead, as shown in Fig. 1f, the upturn can be fitted by CN(T)=f × CSch(T), where CSch(T) is a full expression of nuclear Schottky-specific heat with a hyperfine coupled Pr moment  and f=0.37 is a dimension-less factor representing the fraction of Pr sites with the dipole moment
and f=0.37 is a dimension-less factor representing the fraction of Pr sites with the dipole moment  (Supplementary Note 4). The corresponding elastic neutron scattering cross section
(Supplementary Note 4). The corresponding elastic neutron scattering cross section  barn is not inconsistent with the low T magnetic scattering cross section of 0.02 barn within the 0.1 meV energy resolution of the experiment (Supplementary Figure S3). Here gJ=4/5, r0=−0.54 × 10−12 cm and
barn is not inconsistent with the low T magnetic scattering cross section of 0.02 barn within the 0.1 meV energy resolution of the experiment (Supplementary Figure S3). Here gJ=4/5, r0=−0.54 × 10−12 cm and  =2/3 is the spherical average of the polarization factor for Ising spins. The reduced frozen moment indicates strong quantum fluctuations33 as does the large value of the real part of the AC-susceptibility χ′(T) in the low T limit (Fig. 1d). The apparent inhomogeneity indicated by f=0.37<1 suggests the weak frozen moment could be an extrinsic feature resulting from extreme sensitivity to chemical inhomogeneity.
=2/3 is the spherical average of the polarization factor for Ising spins. The reduced frozen moment indicates strong quantum fluctuations33 as does the large value of the real part of the AC-susceptibility χ′(T) in the low T limit (Fig. 1d). The apparent inhomogeneity indicated by f=0.37<1 suggests the weak frozen moment could be an extrinsic feature resulting from extreme sensitivity to chemical inhomogeneity.
Assigning in this way the low T upturn to nuclear spins, the electronic entropy obtained by integrating CM/T=(CMN−CN)/T up to 20 K is  , which is close to the value of
, which is close to the value of  for classical ice2,4 (Fig. 1f) and inconsistent with a full static Jahn–Teller distortion34. The inferred zero-field magnetic component CM shows a decade of activated T-dependence between 2 K and 0.2 K (Fig. 1f, inset). The corresponding activation energy of ΔC=0.72(1) K is approximately half of that associated with AC-susceptibility data Δχ=1.62(3) K. Note, however, that the above interpretation is not unique and we cannot exclude the possibility that the low T upturn in CMN(T) involves both nuclear and electronic spin entropy.
for classical ice2,4 (Fig. 1f) and inconsistent with a full static Jahn–Teller distortion34. The inferred zero-field magnetic component CM shows a decade of activated T-dependence between 2 K and 0.2 K (Fig. 1f, inset). The corresponding activation energy of ΔC=0.72(1) K is approximately half of that associated with AC-susceptibility data Δχ=1.62(3) K. Note, however, that the above interpretation is not unique and we cannot exclude the possibility that the low T upturn in CMN(T) involves both nuclear and electronic spin entropy.
Discussion
From the multiple streams of distinct but consistent data presented, the following key characteristics of Pr2Zr2O7 emerge. (1) Strong quantum fluctuations: At T=0.1 K, >90% of the magnetic scattering cross section is inelastic, the attempt frequency associated with the activated AC susceptibility is three orders of magnitude larger than for classical spin ice, and the nuclear Schottky anomaly is suppressed below that for a classical frozen state both in terms of moment density and magnitude. (2) Weak static correlations: while exponentially activated specific heat and AC susceptibility data, elastic magnetic neutron scattering, and the nuclear Schottky anomaly consistently indicate some spin-freezing, this could be an extrinsic consequence of weak chemical inhomogeneities. (3) Spin-ice-like correlations at long times: the wave vector dependence of the lowest energy scattering detected features pinch points, the width of which is consistent with the inferred chemical defect density. While further experimental work is required to fully determine the ground state of Pr2Zr2O7 in the clean limit, it is safe to say that it features quantum fluctuations of magnetic monopoles and is unlike any previously documented in an insulating crystalline magnet. The interplay between monopolar quantum dynamics and itinerant electrons may have an important role in the isostructural Kondo lattice system Pr2Ir2O7 (refs 19, 20).
Methods
Sample preparation
Single crystalline samples of Pr2Zr2O7 were grown by a floating zone method35. The orientation of each crystals was established by X-ray Laue diffraction. Energy dispersive X-ray analysis found no impurity phases and determined the Pr/Zr ratio to be 0.94(3). Synchrotron X-ray diffraction measurements were performed at SPring-8. Structure analysis, detailed in Supplementary Note 1, confirmed the pyrochlore crystal structure with  symmetry. The crystal structure information is provided in Supplementary Tables S1 and S2. Further analysis of the diffraction data indicates no significant site mixing beyond the detection limit, but Pr-deficiency at the ~1% level (Supplementary Figures S1, S2, and Supplementary Note 1). A single crystal of the non-magnetic analog La2Zr2O7 was also grown by a floating zone method, and used to approximate the lattice specific heat of Pr2Zr2O7.
symmetry. The crystal structure information is provided in Supplementary Tables S1 and S2. Further analysis of the diffraction data indicates no significant site mixing beyond the detection limit, but Pr-deficiency at the ~1% level (Supplementary Figures S1, S2, and Supplementary Note 1). A single crystal of the non-magnetic analog La2Zr2O7 was also grown by a floating zone method, and used to approximate the lattice specific heat of Pr2Zr2O7.
Measurement of magnetic properties
The temperature-dependence of the DC magnetization at a field of 1000 Oe above 2 K was measured using a commercial SQUID magnetometer. The temperature dependence of the AC susceptibility at an excitation field of 0.3 Oe below 5 K was measured down to 20 mK in a dilution refrigerator through a mutual inductance method. For both measurements, the field was applied along the [111] direction. The AC susceptibility data sets were scaled to data collected at 1000 Oe for temperatures above 2 K. For all data, a demagnetization correction was made with a demagnetization factor N=0.2 obtained by approximating the sample shape as a rectangular prism36. The temperature-dependence of the specific heat was measured by a thermal relaxation method down to 0.07 K. A thin platelet single crystal with a (111) surface normal was used to achieve good thermal contact. Details regarding the analysis of specific heat date are provided in Supplementary Note 4.
Neutron scattering measurements
Neutron scattering measurements were carried out on a 0.8 cm3 single crystal sample using the MACS spectrometer at the NIST Center for Neutron Research for energy transfer below 2 meV and the ARCS spectrometer at the Spallation Neutron Source, Oak Ridge National Laboratories for energy transfer up to 120 meV. The detailed methods of data collection and analysis employed for ARCS and MACS are described in Supplementary Notes 2 and 3 respectively.
Additional information
How to cite this article: Kimura, K. et al. Quantum fluctuations in spin-ice-like Pr2Zr2O7. Nat. Commun. 4:1934 doi: 10.1038/ncomms2914 (2013).
References
Bramwell, S. T. & Gingras, M. J. P. Spin ice state in frustrated magnetic pyrochlore materials. Science 294, 1495 (2001).
Ramirez, A. P. Hayashi, A. Cava, R. J. Siddharthan, R. & Shastry, B. S. Zero-point entropy in ‘spin ice’. Nature 399, 333–335 (1999).
Bernal, J. D. & Fowler, R. A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions. J. Chem. Phys. 1, 515–548 (1933).
Pauling, L. The structure and entropy of ice and of other crystals with some randomness of atomic arrangement. J. Am. Chem. Soc. 57, 2680 (1935).
Castelnovo, C. Moessner, R. & Sondhi, S. L. Magnetic monopoles in spin ice. Nature 451, 42–45 (2008).
Ryzhkin, I. A. Magnetic relaxation in rare-earth oxide pyrochlores. J. Exp. Theor. Phys. 101, 481–486 (2005).
Henley, C. L. Power-law spin correlations in pyrochlore antiferromagnets. Phys. Rev. B 71, 014424 (2005).
Morris, D. J. P. et al. Dirac strings and magnetic monopoles in the spin ice Dy2Ti2O7 . Science 326, 411–414 (2009).
Fennell, T. et al. Magnetic coulomb phase in the spin ice Ho2Ti2O7 . Science 326, 415–417 (2009).
Jaubert, L. D. C. & Holdsworth, P. C. W. Signature of magnetic monopole and Dirac string dynamics in spin ice. Nat. Phys. 5, 258–261 (2009).
Boucher, J. P. et al. Solitons in the one-dimensional antiferromagnet TMMC. Solid State Commun. 33, 171–174 (1980).
Hermele, M. Fisher, M. P. A. & Balents, L. Pyrochlore photons: The U(1) spin liquid in a S=1/2 three-dimensional frustrated magnet. Phys. Rev. B 69, 064404 (2004).
Moessner, R. & Sondhi, S. L. Three-dimensional resonating-valence-bond liquids and their excitations. Phys. Rev. B 68, 184512 (2003).
Banerjee, A. Isakov, S. V. Damle, K. & Kim, Y. B. Unusual liquid state of hard-core bosons on the pyrochlore lattice. Phys. Rev. Lett. 100, 047208 (2008).
Shannon, N. Sikora, O. Pollmann, F. Penc, K. & Fulde, P. Quantum Ice: a Quantum Monte Carlo study. Phys. Rev. Lett. 108, 067204 (2012).
Giamarchi, T. Quantum Physics in One Dimension Oxford University Press: Oxford, (2004).
Gardner, J. S. Gingras, M. J. P. & Greedan, J. E. Magnetic pyrochlore oxides. Rev. Mod. Phys. 82, 53–107 (2010).
Molavian, H. R. Gingras, M. J. P. & Canals, B. Dynamically induced frustration as a route to a quantum spin ice state in Tb2Ti2O7 via virtual crystal field excitations and quantum many-body effects. Phys. Rev. Lett. 98, 157204 (2007).
Nakatsuji, S. et al. Metallic spin-liquid behavior of the geometrically frustrated Kondo lattice Pr2Ir2O7 . Phys. Rev. Lett. 96, 087204 (2006).
Machida, Y. Nakatsuji, S. Onoda, S. Tayama, T. & Sakakibara, T. Time-reversal symmetry breaking and spontaneous hall effect without magnetic dipole order. Nature 463, 210–213 (2010).
Zhou, H. D. et al. Dynamic spin ice: Pr2Sn2O7 . Phys. Rev. Lett. 101, 227204 (2008).
Hodges, J. A. et al. First-order transition in the spin dynamics of geometrically frustrated Yb2Ti2O7 . Phys. Rev. Lett. 88, 077204 (2002).
Thompson, J. D. et al. Rods of neutron scattering intensity in Yb2Ti2O7: compelling evidence for significant anisotropic exchange in a magnetic pyrochlore oxide. Phys. Rev. Lett. 106, 187202 (2011).
Ross, K. A. Savary, L. Gaulin, B. D. & Balents, L. Quantum excitations in quantum spin ice. Phys. Rev. X 1, 021002 (2011).
Chang, L.-J. et al. Higgs transition from magnetic coulomb liquid to a ferromagnet in Yb2Ti2O7 . Nat. Commun. 3, 992 (2012).
Onoda, S. & Tanaka, Y. Quantum fluctuations in the effective pseudospin-1/2 model for magnetic pyrochlore oxides. Phys. Rev. B 83, 094411 (2011).
Snyder, J. et al. Low-temperature spin freezing in the Dy2Ti2O7 spin ice. Phys. Rev. B 69, 064414 (2004).
Matsuhira, K. Hinatsu, Y. & Sakakibara, T. Novel dynamical magnetic properties in the spin ice compound Dy2Ti2O7 . J. Phys. Condens. Matter 13, L737 (2001).
Bramwell, S. T. et al. Spin correlations in Ho2Ti2O7: a dipolar spin ice system. Phys. Rev. Lett. 87, 047205 (2001).
Petit, S. Bonville, P. Robert, J. Decorse, C. & Mirebeau, I. Spin liquid correlations, anisotropic exchange, and symmetry breaking in Tb2Ti2O7 . Phys. Rev. B 86, 174403 (2012).
Onoda, S. & Tanaka, Y. Quantum melting of spin ice: Emergent cooperative quadrupole and chirality. Phys. Rev. Lett. 105, 047201 (2010).
Lee, S. Onoda, S. & Balents, L. Generic quantum spin ice. Phys. Rev. B 86, 104412 (2012).
Bertin, E. et al. Effective hyperfine temperature in frustrated Gd2Sn2O7: two level model and 155Gd Mössbauer measurements. Eur. Phys. J. B 27, 347–354 (2002).
Chapuis, Y. et al. Evidence from thermodynamic measurements for a singlet crystal-field ground state in pyrochlore Tb2Sn2O7 and Tb2Ti2O7 . Phys. Rev. B 82, 100402 (2010).
Matsuhira, K. et al. Spin freezing in the pyrochlore antiferromagnet Pr2Zr2O7 . J. Phys. Conf. Ser. 145, 012031 (2009).
Aharoni, A. Demagnetizing factors for rectangular ferromagnetic prisms. J. Appl. Phys. 83, 3432 (1998).
Acknowledgements
We thank Y. Karaki, Y. Shimura, T. Sakakibara, K. Kuga, M. Takigawa, T. M. McQueen, S. Koohpayeh, K. Matsuhira, Y. Nambu, A.A. Nugroho, Y. Ohta, S. Onoda, R. Satake, O. Tchernyshyov and Y. Wan for useful discussions. This work is partially supported by Grant-in-Aid for Scientific Research (Nos. 21684019 and 23740259) from JSPS, by Grant-in-Aid for Scientific Research on Priority Areas (No. 19052003) and Grant-in-Aid for JSPS Fellows from MEXT, Japan, by Global COE Program ‘the Physical Sciences Frontier’, MEXT, Japan, by PRESTO of JST, by a Toray Science and Technology Grant and by US-Japan Cooperative Program, ISSP. Work at IQM was supported by the US DoE, office of Basic Energy Sciences, Division of Material Sciences and Engineering under DE-FG02-08ER46544. This work utilized facilities supported in part by the NSF under DMR-0944772. Research conducted at ORNL’s Spallation Neutron Source was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, US Department of Energy. Part of this work was conducted while CB was a JSPS fellow at ISSP. The use of the Materials Design and Characterization Laboratory at ISSP is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
S.N. conceived the project. S.N. and C.B. coordinated experiments. K.K. and S.N. performed synthesis, crystal growth, and magnetic susceptibility measurements. J.W., C.B., S.N., and K.K. collected and analyzed thermodynamic and neutron diffraction data. M.B.S. collected crystal field inelastic scattering data, E.N. and H.S. collected and analyzed synchrotron X-ray diffraction data. S.N. C.B. K.K. and J.W. wrote the paper. All authors critically reviewed the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S4, Supplementary Tables S1-S4, Supplementary Notes 1-4 and Supplementary References (PDF 1241 kb)
Rights and permissions
About this article
Cite this article
Kimura, K., Nakatsuji, S., Wen, JJ. et al. Quantum fluctuations in spin-ice-like Pr2Zr2O7. Nat Commun 4, 1934 (2013). https://doi.org/10.1038/ncomms2914
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2914
This article is cited by
-
Magnon thermal Hall effect via emergent SU(3) flux on the antiferromagnetic skyrmion lattice
Nature Communications (2024)
-
Spin–orbital liquid state and liquid–gas metamagnetic transition on a pyrochlore lattice
Nature Physics (2023)
-
Chemical design of electronic and magnetic energy scales of tetravalent praseodymium materials
Nature Communications (2023)
-
Towards understanding the magnetic properties of the breathing pyrochlore compound Ba3Yb2Zn5O11through single-crystal studies
npj Quantum Materials (2022)
-
Giant isotropic magneto-thermal conductivity of metallic spin liquid candidate Pr2Ir2O7 with quantum criticality
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.