Abstract
Heat flow in nanomaterials is an important area of study, with both fundamental and technological implications. However, little is known about heat flow in two-dimensional devices or interconnects with dimensions comparable to the phonon mean free path. Here we find that short, quarter-micron graphene samples reach ~35% of the ballistic thermal conductance limit up to room temperature, enabled by the relatively large phonon mean free path (~100 nm) in substrate-supported graphene. In contrast, patterning similar samples into nanoribbons leads to a diffusive heat-flow regime that is controlled by ribbon width and edge disorder. In the edge-controlled regime, the graphene nanoribbon thermal conductivity scales with width approximately as ~W1.80.3, being about 100 W m−1 K−1 in 65-nm-wide graphene nanoribbons, at room temperature. These results show how manipulation oftwo-dimensional device dimensions and edges can be used to achieve full control of their heat-carrying properties, approaching fundamentally limited upper or lower bounds.
Similar content being viewed by others
Introduction
The thermal properties of graphene are derived from those of graphite and are similarly anisotropic. The in-plane thermal conductivity of isolated graphene is high, >2,000 W m−1 K−1 at room temperature, due to the strong sp2 bonding and relatively small mass of carbon atoms1,2,3. Heat flow in the cross-plane direction is nearly a 1,000 times weaker, limited by van der Waals interactions with the environment (for graphene)4 or between graphene sheets (for graphite)1,2. Recent studies have suggested that the thermal conductivity of graphene is altered when in contact with a substrate through the interaction between vibrational modes (phonons) of graphene and those of the substrate5,6,7,8. However, an understanding of heat-flow properties in nanometre-scale samples of graphene (or any other two-dimensional (2D) materials) is currently lacking.
By comparison, most graphene studies have focused on its electrical properties when confined to scales on the order of the carrier mean free path (mfp)9,10,11,12,13,14. For example, these studies have found that ‘short’ devices exhibit near-ballistic behaviour9 and Fabry–Perot wave interference12, whereas ‘narrow’ nanoribbons display a steep reduction of charge-carrier mobility11,13. Previous studies do exist for heat flow in three-dimensional (3D) structures, such as nanowires and nanoscale films. For instance, ballistic heat flow was observed in suspended GaAs bridges15 and silicon nitride membranes16 at low temperatures, of the order 1 K. Conversely, suppression of thermal conductivity due to strong edge-scattering effects was noted in narrow and rough silicon nanowires17,18, up to room temperature. Yet, such effects have not been studied in 2D materials like graphene, and ballistic heat conduction has not been previously observed near room temperature in any material.
In this work we find that the thermal properties of graphene can be tuned in nanoscale devices comparable in size to the intrinsic phonon mfp. (By ‘intrinsic’ thermal conductivity or phonon mfp, we refer to that in large samples without edge effects, typically limited by phonon–phonon scattering in suspended graphene3 and by substrate scattering in supported graphene6; here λ≈100 nm at room temperature, as we will show.) We find that the thermal conductance of ‘short’ quarter-micron graphene devices reaches up to 35% of theoretical ballistic upper limits19. However, the thermal conductivity of ‘narrow’ graphene nanoribbons (GNRs) is greatly reduced compared with that of ‘large’ graphene samples. Importantly, we uncover that nanoengineering the GNR dimensions and edges is responsible for altering the effective phonon mfp, shifting heat flow from quasi-ballistic to diffusive regimes. These findings are highly relevant for all nanoscale graphene devices and interconnects, also suggesting new avenues to manipulate thermal transport in 2D and quasi-one-dimensional systems.
Results
Test structures and measurements
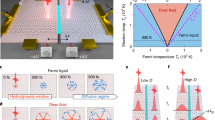
Figure 1 illustrates several of our experimental test structures, showing graphene and GNR arrays supported on a SiO2/Si substrate (see Methods and Supplementary Note S1). Long, parallel metal lines serve as heater and thermometer sensors5,20, electrically insulated from the graphene by a thin SiO2 layer. We perform heat-flow measurements from 20 to 300 K on unpatterned graphene (Fig. 1a), control samples with the graphene etched off (Fig. 1b) and arrays of GNR widths W≈130, 85, 65 and 45 nm (Fig. 1c and Supplementary Fig. S2). Figure 1f shows the Raman spectra of representative samples, with no discernible D peak (no defects) in unpatterned graphene4 and a D/G peak ratio of GNRs consistent with the presence of edge disorder14,21.
(a) Scanning electron microscopy image of parallel heater and sensor metal lines with ~260 nm separation, on top of graphene sample (colourized for emphasis). A thin SiO2 layer under the metal lines provides electrical insulation and thermal contact with the graphene beneath (see Methods and Supplementary Note S1). (b) Similar sample after graphene etch, serving as control measurement for heat flow through contacts and SiO2/Si underlayers. (c) Heater and sensor lines across array of graphene nanoribbons (GNRs). (d) Magnified portion of array with GNR widths ~65 nm; inset shows atomic force microscopy image of GNRs. Scale bars of a–d, 2, 1, 2 and 1 μm, respectively. (e) 3D simulation of experimental structure, showing temperature distribution with current applied through heater line. (f) Raman spectra of unpatterned graphene sample (bottom curve) and GNRs (upper curves, offset for clarity). Inset shows scaling of Raman D to G peak area versus GNR width, consistent with the enhanced role of edge disorder in narrower GNRs14,21,35.
The measurement proceeds as follows. We pass a heating current through one metal line, which sets up a temperature gradient across the sample, and we monitor changes in electrical resistance of the opposite electrode (see Methods and Supplementary Note S2). Both electrode resistances are calibrated over the full temperature range for each sample, allowing us to convert measured changes of resistance into changes of sensor temperature ΔTS, as a function of heater power PH (Supplementary Fig. S5). We also perform measurements after removing the exposed graphene with an oxygen plasma etch (Fig. 1b). This allows us to obtain the thermal properties of the parallel heat-flow path through the contacts, supporting SiO2 and substrate (Supplementary Figs S4 and S8). As a check on our method, we find the thermal conductivity of our SiO2 layer in excellent agreement with well-known data from the literature (Supplementary Note S4 and Supplementary Fig. S8) over the full temperature range. As a result of this exercise, we were also able to fit the thermal resistance of the SiO2–Si interface (Supplementary Fig. S8c and Supplementary Eq. S1), generating one of the few available data sets on this quantity, to our knowledge.
To extract the thermal properties of our samples, we use 3D simulations of the structures with dimensions obtained from measurements by scanning electron microscopy and atomic force microscopy, as shown in Fig. 1d and Supplementary Fig. S7. The model matches the measured and simulated ΔTS and PH, fitting the thermal conductance G between the heater and the thermometer. The 3D simulations automatically include all known contact-resistance effects, including those of the graphene–SiO2 and SiO2–metal interfaces, matched against data from the literature and our control experiments (Supplementary Note S3). To provide some simple estimates, the contact thermal resistance (per electrode width) is RC≈0.7 m. KW−1, the ‘wide’ unpatterned graphene thermal resistance is RG≈2.5 m. KW−1 and that of the GNR arrays is in the range RGNR≈4–32 m. KW−1 (from widest to narrowest). The graphene is not patterned under the electrodes; thus, the contact resistance remains the same for all samples. The 3D simulations also account for heat spreading through the underlying SiO2, and our error bars include various uncertainties in all parameters (Supplementary Note S6).
Figure 2a displays in-plane thermal conductance per area (G/A) for our GNRs, for one of our unpatterned ‘short but wide’ samples (L≈260 nm, W≈12 μm), and for the ‘large’ sample (L≈10 μm) of Seol et al.6 Here A is the cross-sectional area of heat flow, A=WH, where W is the width and H=0.335 nm is the thickness of the graphene samples. At the same time Fig. 3 displays schematics of the size effects and the three transport regimes expected, corresponding to the samples measured in Fig. 2. Figure 2a also shows the theoretical ballistic thermal conductance of graphene22,23,24, Gball/A, calculated with the approach listed in Supplementary Note S9. By comparison, our ‘short’ sample (schematic in Fig. 3b) has a thermal conductance ~35% of Gball/A at 200 K and ~30% at room temperature, indicating a regime of quasi-ballistic phonon transport (other similar samples are shown in Supplementary Fig. S9d). In contrast, the ‘large’ sample from Seol et al.6 (schematic in Fig. 3a) has a conductance per cross-sectional area <2% of the ballistic limit, being in the diffusive transport regime as expected (W, L≫λ).
(a) Thermal conductance per cross-sectional area (G/A) versus temperature for our GNRs (L≈260 nm, W as listed, see Fig. 3c), a ‘short’ unpatterned sample (L≈260 nm, W≈12 μm, see Fig. 3b) and a ‘large’ sample from Seol et al.6 (L≈10 μm, W≈2.4 μm, see Fig. 3a). The short but wide graphene sample attains up to ~35% of the theoretical ballistic heat-flow limit22,23,24 (also see Supplementary Fig. S9). (b) Thermal conductivity for the same samples as in a (also see Supplementary Fig. S10). (c) Thermal conductivity reduction with length for ‘wide’ samples (W λ), compared with the ballistic limit (kball=GballL/A) at several temperatures. Symbols are data for our ‘short’ unpatterned graphene samples (Figs 1a and 3b), and ‘large’ samples of Seol et al.6 (Fig. 3a). Solid lines are model from equation 1. (d) Thermal conductivity reduction with width for GNRs, all with L≈260 nm (Figs 1c,d and 3c). Solid symbols are experimental data from b, open symbols are interpolations for the listed temperature. Lines are fitted model from equation 2, revealing a scaling as ~W1.80.3 in the edge-limited regime. The thermal conductivity of plasma-etched GNRs in this work appears slightly lower than that estimated for GNRs from unzipped nanotubes13 at a given width, consistent with a stronger effect of edge disorder35. Also see Supplementary Fig. S11.
λ), compared with the ballistic limit (kball=GballL/A) at several temperatures. Symbols are data for our ‘short’ unpatterned graphene samples (Figs 1a and 3b), and ‘large’ samples of Seol et al.6 (Fig. 3a). Solid lines are model from equation 1. (d) Thermal conductivity reduction with width for GNRs, all with L≈260 nm (Figs 1c,d and 3c). Solid symbols are experimental data from b, open symbols are interpolations for the listed temperature. Lines are fitted model from equation 2, revealing a scaling as ~W1.80.3 in the edge-limited regime. The thermal conductivity of plasma-etched GNRs in this work appears slightly lower than that estimated for GNRs from unzipped nanotubes13 at a given width, consistent with a stronger effect of edge disorder35. Also see Supplementary Fig. S11.
(a) Diffusive heat transport in ‘large’ samples with dimensions much greater than the intrinsic phonon mfp (L, W λ). This regime corresponds to the samples measured in both substrate-supported6 and -suspended graphene2,3 studies to date. (b) Quasi-ballistic heat flow in ‘short but wide’ samples (L~λ and W
λ). This regime corresponds to the samples measured in both substrate-supported6 and -suspended graphene2,3 studies to date. (b) Quasi-ballistic heat flow in ‘short but wide’ samples (L~λ and W λ). This regime corresponds to our geometry shown in Fig. 1a, with L≈260 nm and W≈12 μm. (c) Return to a diffusive heat transport regime as the sample width is narrowed down, and phonon scattering with edge roughness (of r.m.s. Δ) begins to dominate. This regime corresponds to our arrays of GNRs from Fig. 1c–e (L≈260 nm and W varying from 45 to 130 nm). A fourth regime (long L, narrow W) is not shown here, but it can be easily understood from the above.
λ). This regime corresponds to our geometry shown in Fig. 1a, with L≈260 nm and W≈12 μm. (c) Return to a diffusive heat transport regime as the sample width is narrowed down, and phonon scattering with edge roughness (of r.m.s. Δ) begins to dominate. This regime corresponds to our arrays of GNRs from Fig. 1c–e (L≈260 nm and W varying from 45 to 130 nm). A fourth regime (long L, narrow W) is not shown here, but it can be easily understood from the above.
Length dependence of thermal conductivity
We recall that in the ballistic limit (L λ), the conductance, rather than the conductivity, approaches a constant at a given temperature22,23,24, Gball(T). Nevertheless, the thermal conductivity is the parameter typically used for calculating heat transport in practice, and for comparing different materials and systems. Thus, the well-known relationship k=(G/A)L imposes the conductivity k to become a function of length in the ballistic regime and to decrease as L is reduced. This situation becomes evident when we plot the thermal conductivity in Fig. 2b, finding k≈320 W m−1 K−1 for our ‘short’ and wide samples at room temperature (schematic Fig. 3b), almost a factor of two lower than the large graphene6 (schematic Fig. 3a). We note that both unpatterned samples here and in Seol et al.6 were supported by SiO2, showed no discernible defects in the Raman spectra and the measurements were repeated over three samples (Supplementary Note S5 and Supplementary Fig. S9), with similar results obtained each time.
λ), the conductance, rather than the conductivity, approaches a constant at a given temperature22,23,24, Gball(T). Nevertheless, the thermal conductivity is the parameter typically used for calculating heat transport in practice, and for comparing different materials and systems. Thus, the well-known relationship k=(G/A)L imposes the conductivity k to become a function of length in the ballistic regime and to decrease as L is reduced. This situation becomes evident when we plot the thermal conductivity in Fig. 2b, finding k≈320 W m−1 K−1 for our ‘short’ and wide samples at room temperature (schematic Fig. 3b), almost a factor of two lower than the large graphene6 (schematic Fig. 3a). We note that both unpatterned samples here and in Seol et al.6 were supported by SiO2, showed no discernible defects in the Raman spectra and the measurements were repeated over three samples (Supplementary Note S5 and Supplementary Fig. S9), with similar results obtained each time.
The transition of 2D thermal conductivity from diffusive to ballistic can be captured through simple models25, similar to the apparent mobility reduction during quasi-ballistic charge transport observed in short-channel transistors26,27:

The first equality is a ‘three-colour’ model with p the phonon mode (longitudinal acoustic; transverse; flexural), Gp,ball calculated using the appropriate dispersion19 and ∑kp,diff=kdiff the diffusive thermal conductivity (~600 W m−1 K−1 at 300 K)6. A simpler ‘gray’ approximation can also be obtained by dropping the p index, k(L)≈[A/(LGball)+1/kdiff]−1, where Gball/A≈4.2 × 109 W K−1 m−2 at room temperature19 (see Supplementary Note S9). The second expression in equation 1 is a Landauer-like model25,28, with π/2 accounting for angle averaging29 in 2D to obtain the phonon backscattering mfp. For convenience, we note that the ballistic thermal conductance of graphene can be approximated analytically as Gball/A≈[1/(4.4 × 105 T1.68)+1/(1.2 × 1010)]−1 W K−1 m−2 over the temperature range 1–1,000 K, as a fit to full numerical calculations (Supplementary Fig. S16).
We compare the simple models in equation 1 with the experiments in Fig. 2c and find good agreement over a wide temperature range. The comparison also yields our first estimate of the intrinsic phonon mfp in SiO2-supported graphene, λ≈(2/π)kdiff/(Gball/A)≈90 nm at 300 K and 115 nm at 150 K. (The same argument estimates an intrinsic phonon mfp λ≈300–600 nm in freely suspended graphene at 300 K, if a thermal conductivity 2,000–4,000 W m−1 K−1 is used1,2,3.) This phonon mfp is the key length scale which determines when the thermal conductivity of a sample becomes a function of its dimensions, in other words when L and W become comparable to λ. On the basis of Fig. 2c, we note that quasi-ballistic heat-flow effects should become non-negligible in all SiO2-supported graphene devices shorter than ~1 μm.
Width dependence of thermal conductivity
We now turn to the width dependence of heat flow in narrow GNRs. Our experimental data in Fig. 2b show a clear decrease of thermal conductivity as the width W is reduced to a size regime comparable to the intrinsic phonon mfp. For instance, at room temperature k≈230, 170, 100 and 80 W m−1 K−1 for GNRs of W≈130, 85, 65 and 45 nm, respectively, and same L≈260 nm. To understand this trend, we consider k limited by phonon scattering with edge disorder30,31 through a simple empirical model with a functional form suggested by previous work on rough nanowires32,33 and GNR mobility34:

Here Δ is the root-mean-square (r.m.s.) edge roughness (Fig. 3c) and k(L) is given by equation 1. The solid lines in Fig. 2d show good agreement with our GNR data (L≈260 nm) using Δ=0.6 nm and a best-fit exponent n=1.8±0.3. The parameter c=0.04 W m−1 K−1 can be used to fit the room-temperature data set and additional fitting discussion is provided in the Supplementary Note S9. (Note that we cannot assign an overly great physical meaning to the parameter c, because the empirical model can only fit Δn/c, not Δ or c independently). The simple model appears to be a good approximation in a regime with Δ W, where the data presented here were fitted. However, it is likely that this simple functional dependence would change in a situation with extreme edge roughness18, where the roughness correlation length (which cannot be directly quantified here) could also have an important role.
W, where the data presented here were fitted. However, it is likely that this simple functional dependence would change in a situation with extreme edge roughness18, where the roughness correlation length (which cannot be directly quantified here) could also have an important role.
Nevertheless, the nearly W-squared dependence of thermal conductivity in narrow GNRs with edge roughness is consistent with previous findings for rough nanowires32,33, and also similar to that suggested by theoretical studies of GNR electron mobility34. The precise scaling with Δ is ostensibly more complex30,31 than can be captured in a simple model, as it depends on details of the phonon dispersion, the phonon wave vector and indirectly on temperature. However, the Δ estimated from the simple model presented above is similar to that from extensive numerical simulations below, and to that measured by transmission electron microscopy on GNRs prepared under similar conditions35. Thus, the simple expressions given above can be taken as a practical model for heat flow in substrate-supported GNRs with edge roughness (Δ W) over a wide range of dimensions, corresponding to all size regimes in Fig. 3.
W) over a wide range of dimensions, corresponding to all size regimes in Fig. 3.
Discussion
We first revisit the effects of measurement contacts and how they relate to the interpretation of sample length in the quasi-ballistic heat-flow regime. As in studies of quasi-ballistic electrical transport26,27, we defined the ‘channel length’ L as the inside edge-to-edge distance between the heater and thermometer electrodes (Fig. 3c). Simple ballistic theory assumes contacts with an infinite number of modes and instant thermalization of phonons at the edges of the contacts. The former is well approximated here by electrodes two hundred times thicker than the graphene sheet; however, phonons may travel some distance below the contacts before equilibrating. The classical, continuum analogue of this aspect is represented by the thermal transfer length (LT) of heat flow from the graphene into the contacts3,36, which is automatically taken into account in our 3D simulations (Fig. 1e). However, a subcontinuum perspective37 reveals that graphene phonons only thermally equilibrate after travelling one mfp below the contacts. Previous measurements of oxide-encased graphene5 had estimated a thermal conductivity kenc=50–100 W m−1 K−1, which suggests a phonon mfp λenc=(2kenc/π)/(Gball/A)≈8–15 nm under the contacts. This adds at most 12% to our assumption of edge-to-edge sample length (here L≈260 nm), a small uncertainty which is comparable to the sample-to-sample variation from fabrication, and to the size of the symbols in Fig. 2c. (The relatively low thermal conductivity of encased monolayer graphene5 is due to scattering with the SiO2 sandwich, although some graphene damage from the SiO2 evaporation38 on top is also possible.)
To gain deeper insight into our experimental results, we employ a numerical solution of the Boltzmann transport equation (BTE) with a complete phonon dispersion31,39. Our approach is similar to previous work6,40, but accounting for quasi-ballistic phonon propagation and edge disorder scattering in short and narrow GNRs, respectively (see Methods and Supplementary Notes S7 and S8). Figure 4a finds good agreement of thermal conductivity between our measurements and the BTE model across all samples and temperatures. We obtained the best fit for GNRs of width 130 and 85 nm with r.m.s. edge roughness Δ=0.25 and 0.3 nm, where the gray bands in Fig. 4a correspond to ±5% variation around these values. For GNRs of widths 65 and 45 nm, the gray bands correspond to edge roughness ranges Δ=0.35–0.5 and 0.5–1 nm, respectively. We note that unlike the empirical model of equation 2, the best-fit BTE simulations do not use a unique value of edge roughness Δ. This could indicate some natural sample-to-sample variation in edge roughness from the fabrication conditions, but it could also be due to certain edge-scattering physics (such as edge-roughness correlation18 and phonon localization41), which are not yet captured by the BTE model.
(a) Comparison of Boltzmann transport model (lines) with experimental data (symbols, same as Fig. 2b, but here on linear scale). (b) Computed scaling of phonon mfp versus width, for two sample lengths as listed. Longitudinal acoustic (LA) and transverse (TA) phonons with long intrinsic mfp are subject to stronger size effects from edge scattering than flexural (ZA) modes, which are primarily limited by substrate scattering. (c) Estimated contribution of modes to thermal conductivity versus edge roughness Δ for a wide sample and a narrow GNR. Similar to W, changes in Δ also more strongly affect LA and TA modes, until substrate scattering begins to dominate. (d) Phonon mfp versus energy (frequency) for a large sample and a narrow GNR. Low-frequency modes are strongly affected by substrate scattering, such that effects of edge roughness are most evident for ħω>15 meV. Panels b–d are all at room temperature. Also see Supplementary Figs S13 and S15.
Figure 4b examines the scaling of mfps by phonon mode, finding they are strongly reduced as the GNR width decreases below ~200 nm, similar to the thermal conductivity in Fig. 2d. The mfp for each phonon mode is calculated as an average over the entire frequency spectrum, weighted by the frequency-dependent heat capacity and group velocity (Supplementary Eq. S19). We note that longitudinal acoustic (LA) and transverse (TA) modes, which have larger intrinsic mfps, are more strongly affected by the GNR edge disorder. On the other hand, flexural acoustic modes (ZA) are predominantly limited by substrate scattering and consequently suffer less from edge disorder, consistently with recent findings from molecular dynamics simulations7,8.
Increasing edge disorder reduces phonon mfps (Supplementary Fig. S15d), and the thermal conductivity is expected to scale as shown in Fig. 4c. In the BTE model, the edge-roughness scattering is captured using a momentum-dependent specularity parameter (Supplementary Eq. S11), meaning that small wavelength (large momentum q) phonons are more strongly affected by line edge roughness. However, as Δ increases the specularity parameter saturates, marking a transition to fully diffuse edge scattering, and also to a regime where substrate scattering begins to dominate long-wavelength phonons in substrate-supported samples. This transition cannot be captured by the simplified Δn dependence in the empirical model of equation 2.
To further illustrate such distinctions, Fig. 4d displays the energy (frequency ω) dependence of phonon mfps for a ‘small’ GNR and a ‘large’ SiO2-supported graphene sample (corresponding to Fig. 3c and 3a, respectively). Low-frequency substrate scattering (proportional to ~1/ω2) dominates the large sample6,7, whereas scattering with edge disorder affects phonons with wavelengths comparable to, or smaller than, the roughness Δ (see Supplementary Note S7). Therefore, larger Δ can affect more long-wavelength (low energy) phonons, but only up to Δ~1 nm, where the effect of the substrate begins to dominate in the long-wavelength region (also seen in Fig. 4c). Such a separation of frequency ranges affected by substrate and edge scattering could provide an interesting opportunity to tune both the total value and the spectral components of thermal transport in GNRs, by controlling the substrate and edge roughness independently.
Finally, it is instructive to examine some similarities and differences between our findings here versus previous results regarding size effects on charge-carrier mobility in GNRs with dimensions comparable to the phonon or electron mfp. The edge-limited thermal conductivity begins to fall off in GNRs narrower than ~200 nm (Fig. 2d), or twice the intrinsic phonon mfp. A similar trend was noted for the electrical mobility in GNRs11, but with a fall off at widths narrower than ~40 nm (Supplementary Fig. S11). These observations are consistent with the intrinsic electron mfp being several times shorter13,42 than the phonon mfp in SiO2-supported graphene, that is, ~20 nm for the electron mfp versus nearly ~100 nm for the phonon mfp at room temperature. Thus, edge disorder affects thermal transport more strongly than charge transport in GNRs of an intermediate width (40<W<200 nm), an effect that could be used to manipulate charge and heat flow independently in such nanostructures.
In conclusion, we have investigated heat flow in SiO2-supported graphene samples of dimensions comparable to the phonon mfp. Short devices (L~λ, corresponding to Fig. 3b schematic) have thermal conductance much higher than that previously found in micron-sized samples, reaching 35% of the ballistic limit at 200 K and 30% (~1.2 GW K−1 m−2) at room temperature. However, narrow ribbons (W~λ, corresponding to Fig. 3c schematic) show decreased thermal conductivity due to phonon scattering with edge disorder. Thus, the usual meaning of thermal conductivity must be carefully interpreted when it becomes a function of sample dimensions. The results also suggest powerful means to tune heat flow in 2D nanostructures through the effects of sample width, length, substrate interaction and edge disorder.
Methods
Sample fabrication
Graphene monolayers were deposited on SiO2/Si (~290 nm/0.5 mm) substrates by mechanical exfoliation from natural graphite. Graphene thickness and GNR edge disorder were evaluated with Raman spectroscopy4,21,35. Samples were annealed in Ar/H2 at 400 °C for 40 min. Electron (e)-beam lithography was used to pattern the heater and thermometer electrodes as long, parallel, ~200-nm-wide lines with current and voltage probes, with a separation of L≈260 nm (Fig. 1). Electrodes were deposited by successive evaporation of SiO2 (20 nm) for electrical insulation and Ti/Au (30/20 nm) for temperature sensing. Additional e-beam lithography and oxygen plasma etching were performed when needed, to define GNR arrays with pitch ~150 nm and varying widths.
Electrical and thermal measurements
The heater electrode is slowly ramped up (<0.2 mHz) to 1.5 mA. We measured the resistance change of the sensor electrode through a lock-in technique with a frequency of 2,147 Hz and r.m.s. current of 1 μA (carefully verified to avoid additional heating). All electrical measurements were performed in a four-probe configuration, inside a Physical Property Measurement System (Quantum Design).
Numerical simulation
We obtain the thermal conductivity by solving the Boltzmann transport equation in the relaxation time approximation, including scattering at the rough GNR edges31. The simulation uses the phonon dispersion of an isolated graphene sheet, which is a good approximation for SiO2-supported graphene within the phonon frequencies that contribute most to transport8, and at typical graphene–SiO2 interaction strengths7. (However, we note that artificially increasing the graphene–SiO2 coupling, for example, by applying pressure43, could lead to modifications of the phonon dispersion and hybridized graphene–SiO2 modes7.) We assume a graphene monolayer thickness H=0.335 nm and a concentration of 1% 13C isotope point defects2,6. The interaction with the SiO2 substrate is modelled through perturbations to the scattering Hamiltonian6 at small patches where the graphene is in contact with the SiO2, with nominal patch radius a=8.75 nm. Anharmonic three-phonon interactions of both normal and umklapp type are included in the relaxation time (see Supplementary Note S7). An equivalent 2D ballistic scattering rate25,29 ~2vx/L is used in the numerical solution (x is the heat flow direction along graphene) to account for transport in short GNRs.
Additional information
How to cite this article: Bae, M.-H. et al. Ballistic to diffusive crossover of heat flow in graphene ribbons. Nat. Commun. 4:1734 doi: 10.1038/ncomms2755 (2013).
References
Pop, E., Varshney, V. & Roy, A. K. Thermal properties of graphene: fundamentals and applications. MRS Bull. 37, 1273–1281 (2012) .
Balandin, A. A. Thermal properties of graphene and nanostructured carbon materials. Nat. Mater. 10, 569–581 (2011) .
Dorgan, V. E., Behnam, A., Conley, H. J., Bolotin, K. I. & Pop, E. High-field electrical and thermal transport in suspended graphene. Nano Lett doi: 10.1021/nl400197w (2013) .
Koh, Y. K., Bae, M.-H., Cahill, D. G. & Pop, E. Heat conduction across monolayer and few-layer graphenes. Nano Lett. 10, 4363–4368 (2010) .
Jang, W. Y., Chen, Z., Bao, W. Z., Lau, C. N. & Dames, C. Thickness-dependent thermal conductivity of encased graphene and ultrathin graphite. Nano Lett. 10, 3909–3913 (2010) .
Seol, J. H. et al. Two-dimensional phonon transport in supported graphene. Science 328, 213–216 (2010) .
Ong, Z.-Y. & Pop, E. Effect of substrate modes on thermal transport in supported graphene. Phys. Rev. B 84, 075471 (2011) .
Qiu, B. & Ruan, X. Reduction of spectral phonon relaxation times from suspended to supported graphene. Appl. Phys. Lett. 100, 193101 (2012) .
Miao, F. et al. Phase-coherent transport in graphene quantum billiards. Science 317, 1530–1533 (2007) .
Huang, B., Yan, Q., Li, Z. & Duan, W. Towards graphene nanoribbon-based electronics. Front. Phys. China 4, 269–279 (2009) .
Yang, Y. & Murali, R. Impact of size effect on graphene nanoribbon transport. IEEE Elec. Dev. Lett. 31, 237–239 (2010) .
Wang, X. et al. Graphene nanoribbons with smooth edges behave as quantum wires. Nat. Nanotech. 6, 563–567 (2011) .
Liao, A. D. et al. Thermally limited current carrying ability of graphene nanoribbons. Phys. Rev. Lett. 106, 256801 (2011) .
Behnam, A. et al. Transport in nanoribbon interconnects obtained from graphene grown by chemical vapor deposition. Nano Lett. 12, 4424–4430 (2012) .
Tighe, T. S., Worlock, J. M. & Roukes, M. L. Direct thermal conductance measurements on suspended monocrystalline nanostructures. Appl. Phys. Lett. 70, 2687–2689 (1997) .
Schwab, K., Henriksen, E. A., Worlock, J. M. & Roukes, M. L. Measurement of the quantum of thermal conductance. Nature 404, 974–977 (2000) .
Chen, R. et al. Thermal conductance of thin silicon nanowires. Phys. Rev. Lett. 101, 105501 (2008) .
Lim, J., Hippalgaonkar, K., Andrews, S. C., Majumdar, A. & Yang, P. Quantifying surface roughness effects on phonon transport in silicon nanowires. Nano Lett. 12, 2475–2482 (2012) .
Serov, A. Y., Ong, Z.-Y. & Pop, E. Effect of grain boundaries on thermal transport in graphene. Appl. Phys. Lett. 102, 033104 (2013) .
Stojanovic, N., Berg, J. M., Maithripala, D. H. S. & Holtz, M. Direct measurement of thermal conductivity of aluminum nanowires. Appl. Phys. Lett. 95, 091905 (2009) .
Ryu, S., Maultzsch, J., Han, M. Y., Kim, P. & Brus, L. E. Raman spectroscopy of lithographically patterned graphene nanoribbons. ACS Nano. 5, 4123–4130 (2011) .
Mingo, N. & Broido, D. A. Carbon nanotube ballistic thermal conductance and its limits. Phys. Rev. Lett. 95, 096105 (2005) .
Saito, K., Nakamura, J. & Natori, A. Ballistic thermal conductance of a graphene sheet. Phys. Rev. B 76, 115409 (2007) .
Muñoz, E., Lu, J. & Yakobson, B. I. Ballistic thermal conductance of graphene ribbons. Nano Lett. 10, 1652–1656 (2010) .
Prasher, R. Thermal boundary resistance and thermal conductivity of multiwalled carbon nanotubes. Phys. Rev. B 77, 075424 (2008) .
Shur, M. S. Low ballistic mobility in submicron HEMTs. IEEE Elec. Dev. Lett. 23, 511–513 (2002) .
Wang, J. & Lundstrom, M. Ballistic transport in high electron mobility transistors. IEEE Trans. Electron Devices 50, 1604–1609 (2003) .
Jeong, C., Datta, S. & Lundstrom, M. Full dispersion versus Debye model evaluation of lattice thermal conductivity with a Landauer approach. J. Appl. Phys. 109, 073718 (2011) .
Jeong, C., Kim, R., Luisier, M., Datta, S. & Lundstrom, M. On Landauer versus Boltzmann and full band versus effective mass evaluation of thermoelectric transport coefficients. J. Appl. Phys. 107, 023707 (2010) .
Haskins, J. et al. Control of thermal and electronic transport in defect-engineered graphene nanoribbons. ACS Nano. 5, 3779–3787 (2011) .
Aksamija, Z. & Knezevic, I. Lattice thermal conductivity of graphene nanoribbons: anisotropy and edge roughness scattering. Appl. Phys. Lett. 98, 141919 (2011) .
Martin, P. N., Aksamija, Z., Pop, E. & Ravaioli, U. Reduced thermal conductivity in nanoengineered rough ge and gaas nanowires. Nano Lett. 10, 1120–1124 (2010) .
Sadhu, J. & Sinha, S. Room-temperature phonon boundary scattering below the Casimir limit. Phys. Rev. B 84, 115450 (2011) .
Goharrizi, A. Y., Pourfath, M., Fathipour, M., Kosina, H. & Selberherr, S. An analytical model for line-edge roughness limited mobility of graphene nanoribbons. IEEE Trans. Electron Devices 58, 3725–3735 (2011) .
Xie, L. et al. Graphene nanoribbons from unzipped carbon nanotubes: atomic structures, raman spectroscopy, and electrical properties. J. Am. Chem. Soc. 133, 10394–10397 (2011) .
Grosse, K. L., Bae, M.-H., Lian, F., Pop, E. & King, W. P. Nanoscale Joule heating, Peltier cooling and current crowding at graphene-metal contacts. Nat. Nanotech. 6, 287–290 (2011) .
Siemens, M. E. et al. Quasi-ballistic thermal transport from nanoscale interfaces observed using ultrafast coherent soft X-ray beams. Nat. Mater. 9, 26–30 (2010) .
Ni, Z. H. et al. Tunable stress and controlled thickness modification in graphene by annealing. ACS Nano. 2, 1033–1039 (2008) .
Aksamija, Z. & Knezevic, I. Thermal transport in graphene nanoribbons supported on SiO2 . Phys. Rev. B 86, 165426 (2012) .
Nika, D. L., Pokatilov, E. P., Askerov, A. S. & Balandin, A. A. Phonon thermal conduction in graphene: Role of Umklapp and edge roughness scattering. Phys. Rev. B 79, 155413 (2009) .
Wang, Y., Qiu, B. & Ruan, X. Edge effect on thermal transport in graphene nanoribbons: a phonon localization mechanism beyond edge roughness scattering. Appl. Phys. Lett. 101, 013101 (2012) .
Bae, M.-H., Islam, S., Dorgan, V. E. & Pop, E. Scaling of high-field transport and localized heating in graphene transistors. ACS Nano. 5, 7936–7944 (2011) .
Hsieh, W.-P., Lyons, A. S., Pop, E., Keblinski, P. & Cahill, D. G. Pressure tuning of the thermal conductance of weak interfaces. Phys. Rev. B 84, 184107 (2011) .
Acknowledgements
We thank D. Estrada, B. Howe and A. Bezryadin for assistance with the experimental setup; A. Serov for the numerical phonon dispersion; and J. Seol and L. Shi for providing the original sample dimensions of Seol et al.6 Experiments were carried out in part in the Frederick Seitz Materials Research Laboratory at the University of Illinois. This work was sponsored by a Presidential Early Career (PECASE) award from the Army Research Office (E.P.), the Office of Naval Research (ONR), the Nanotechnology Research Initiative (NRI), the National Science Foundation (NSF) and an NSF CI TraCS Postdoctoral Fellowship (Z.A.).
Author information
Authors and Affiliations
Contributions
M.-H.B. and E.P. conceived the experimental design. M.-H.B. fabricated devices and performed measurements with assistance from Z.L. and Z.-Y.O.; Z.L. extracted thermal transport data from the measurements and carried out all uncertainty analysis. Z.A. and P.N.M. performed Boltzmann transport simulations with input from Z.L., E.P. and I.K.; F.X. obtained all atomic force microscopy images. E.P., Z.L., M.-H.B. and Z.A. cowrote the manuscript, with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S16, Supplementary Tables S1-S2, Supplementary Notes 1-9 and Supplementary References (PDF 2133 kb)
Rights and permissions
About this article
Cite this article
Bae, MH., Li, Z., Aksamija, Z. et al. Ballistic to diffusive crossover of heat flow in graphene ribbons. Nat Commun 4, 1734 (2013). https://doi.org/10.1038/ncomms2755
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2755
This article is cited by
-
Flexible thermoelectrics in crossed graphene/hBN composites
Scientific Reports (2024)
-
Non-stationary elastic wave scattering and energy transport in a one-dimensional harmonic chain with an isotopic defect
Continuum Mechanics and Thermodynamics (2024)
-
Bilinear form and n-soliton thermophoric waves for the variable coefficients (2 + 1)-dimensional graphene sheets equation
Optical and Quantum Electronics (2024)
-
Observation of phonon Poiseuille flow in isotopically purified graphite ribbons
Nature Communications (2023)
-
Unsteady ballistic heat transport in a 1D harmonic crystal due to a source on an isotopic defect
Continuum Mechanics and Thermodynamics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.