Abstract
Coupling the surface state of a topological insulator to an s-wave superconductor is predicted to produce the long-sought Majorana quasiparticle excitations. However, superconductivity has not been measured in surface states when the bulk charge carriers are fully depleted, that is, in the true topological regime relevant for investigating Majorana modes. Here we report measurements of d.c. Josephson effects in topological insulator–superconductor junctions as the chemical potential is moved through the true topological regime characterized by the presence of only surface currents. We compare our results with three-dimensional quantum transport simulations, and determine the effects of bulk/surface mixing, disorder and magnetic field; in particular, we show that the supercurrent is largely carried by surface states, due to the inherent topology of the bands, and that it is robust against disorder. Our results thus clarify key open issues regarding the nature of supercurrents in topological insulators.
Similar content being viewed by others
Introduction
Three-dimensional (3D) topological insulators (TIs), such as Bi2Se3 and Bi2Te3, are characterized by the existence of a bulk-insulating energy gap, gapless Dirac surface states and a π-Berry’s phase1. For 3D TIs coupled to s-wave superconductors, the winding of the superconducting vortices can counteract the π-Berry’s phase, resulting in zero-energy Majorana fermions produced at the interface2,3,4,5. Such Majorana fermions may be topologically protected from decoherence, and could have a significant role in solid-state implementations of a quantum computer. A requisite step in the search for Majorana fermions is to understand the nature and origin of the supercurrent generated between superconducting contacts and a TI. Previous measurements of Bi2Se3- or Bi2Te3-superconductor junctions6,7,8,9 have demonstrated that the supercurrent can be tuned by a gate voltage8 and exhibits Josephson effects such as Fraunhofer patterns6,9; it has also been argued that the supercurrent is carried by surface states, though the mechanism was not well understood6. Fundamental questions remain, particularly concerning the behaviour through the Dirac point and the effects of disorder. We approach these by measuring the supercurrent over a wide-range of gate voltages (chemical potentials)—through a clear ambipolar transport regime—and by comparing our results with full 3D quantum transport calculations that can include disorder. We find that the supercurrent is largely carried by surface states because of protected crystal symmetries, and is only suppressed when bulk/surface mixing is strong or at very low carrier densities. We further find that the supercurrent is not symmetric with respect to the conduction and valence bands, and that the Fraunhofer patterns are similar both within and outside of the topological regime.
Results
Approaching the topological regime
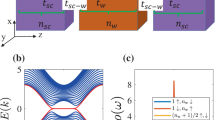
The major obstacles in reaching the topological regime in transport experiments are high n-doping in as-grown TI materials and the further increase of n-doping during mechanical cleavage of crystals10,11,12,13. We implemented three strategies to reduce doping in thin exfoliated films, utilizing (1) Sb-doped TI materials, (2) chemical doping of the top surface and (3) a backgate. It has been previously reported that growing 3D TI materials with in-situ Ca or Sb dopants reduces n-doping10,13,14,15. Thus, we have grown (BixSb2−x)Se3 crystals having x=1.33 (see Methods). Angle-resolved photoemission spectroscopy (ARPES) confirms the topological spectra of the crystals (Fig. 2d). From Fig. 2d, it is evident that the bulk conduction band (BCB) is located at an energy E~0.20 eV above the Dirac point and gapless linear surface states exist inside the bulk bandgap. The total surface carrier density at the bottom of the BCB is estimated to be k2/4π × 2 (two surfaces of a device)~0.8 × 1013 cm−2, where k~0.071 Å−1 was extracted at the bottom of the BCB from the ARPES data along the Γ–K line. Possible hexagonal warping of the Fermi surface could lead to few percent error in the carrier density near the bottom of the BCB16.
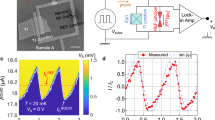
Devices consisted of mechanically exfoliated ~10-nm-thick films on Si/SiO2 substrates10,11,12 (which are used as backgates) having Ti(2.5 nm)/Al(140 nm) contacts (see Methods). We deposited the chemical dopant 2,3,5,6-tetrafluoro-7,7,8,8-tetracyanoquinodimethane (F4-TCNQ) on some devices, as shown schematically in Fig. 1a. F4-TCNQ has a strong electron affinity, and has been shown to effectively remove excess n-doping in Bi2Se3 (ref. 12). A backgate voltage was then used to fully deplete the bulk charge carriers and tune the chemical potential through the Dirac point. It has been shown that once the bulk charge carriers are mostly depleted, the Fermi levels of the top and bottom surface states lock to each other and shift simultaneously, even with a single gate12. In this paper, we show experimental results from two devices, where ‘device 1’ has chemical doping and ‘device 2’ does not. It was possible to use a backgate to deplete bulk carriers in device 2 because of the low n-doping due to Sb; however, in this case a much larger backgate voltage was required to reach the Dirac point. All transport measurements were performed in a dilution refrigerator at the base temperature of T=16 mK. Each device was configured with both a Hall bar geometry and with closely spaced electrodes across which Josephson currents were measured, as shown in Fig. 1a and b.
(a) Device and measurement schematic and (b) scanning electron microscopy image of device 1. The blue dots in a represent 2,3,5,6-tetrafluoro-7,7,8,8-tetracyanoquinodimethane (F4-TCNQ) molecules. The Hall measurement was performed in the Hall bar by applying current I and measuring longitudinal (Vxx) and Hall (VH) voltages, while the Josephson effect was measured in the closely spaced junction by applying current IJ and measuring voltage VJ. The scale bar in b corresponds to 1 μm. (c) I–V curves measured in device 2 at Vg=0 for four different temperatures, showing typical supercurrent behaviour.
Hall measurements
Figure 2 shows resistivity and Hall measurements for device 1 at T=16 mK and with Bperpendicular=35 mT (to suppress superconductivity in the aluminium leads). We observe a peak in resistivity ρxx (minimum in conductivity σxx) and a corresponding sign change in Hall carrier density nH near Vg~−55 V, which signal that the charge carriers change from electrons to holes as the chemical potential passes through the Dirac point. Figure 2 shows that the charge neutrality point seems to coincide with the minimum conductivity (or maximum resistivity) point. The negligible difference of residual densities of electrons and holes in the Hall measurement also implies that the charge neutrality and Dirac points are reached at nearly the same gate voltage17. By comparing the total surface carrier density at the bottom of the BCB calculated from ARPES measurements, nH=0.8 × 1013 cm−2, to the nH versus Vg measured in Fig. 2b, we find that the bottom of the BCB occurs near Vg=−18 V (with a few volt uncertainty due to possible hexagonal warping). This indicates that Vg<−18 V is the topological regime, where only surface states are occupied, while Vg>−18 V is the regime where both surface and bulk states are populated.
(a) Longitudinal resistivity ρxx, (b) Hall carrier density nH and (c) longitudinal conductivity σxx for device 1 as functions of backgate voltage. The maximum in ρxx (min in σxx) and divergence of nH indicate the location of the Dirac point (DP) and the presence of both carrier types. (d) ARPES data of the bulk crystal along the Γ–K line, showing the expected Dirac cone band structure of the surface state. The Dirac point and the bottom of the bulk conductance band (BCB) are indicated by arrows. It is clear from ARPES and Hall data that the system passes through a true topological regime of only surface states.
Josephson effects
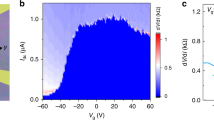
We now turn to measurements of Josephson effects. Figure 1c shows I–V curves measured for device 2 at three different temperatures, for Vg=0. The I–V curves exhibit zero-voltage regimes for currents less than the critical current Ic. Above Ic, a finite voltage is measured as the sample transitions to the normal regime. The critical current can also be modulated by Vg: in Fig. 3b and d, we show two-dimensional plots of differential resistance dV/dI versus current I versus Vg, for devices 1 and 2, respectively. The purple regions where dV/dI=0 indicate superconducting regions, and the boundary corresponds to Ic for a given Vg. Figure 3a and c show the corresponding normal state dV/dI versus Vg for the two-terminal Josephson configuration (taken at B=35 mT). For device 1, the Dirac point is identified with the maximum resistance peak at Vg~−55 V, consistent with the Hall measurement shown in Fig. 2; the Dirac point for device 2 is near Vg~−140 V.
Differential resistance (dV/dI) versus gate voltage in the normal regime (B=35 mT) for (a) device 1 and (c) device 2, showing locations of Dirac points in the Josephson configuration. Two-dimensional plots of dV/dI versus gate voltage Vg and current I for (b) device 1 and (d) device 2. The purple regions show the extent of the supercurrent, where dV/dI=0; the boundaries of these regions correspond to Ic. The bottom of the bulk conduction band is labelled as white dashed lines in b and d.
It is now possible to compare the behaviour of the supercurrent in different transport regimes. Figure 3 shows that in both devices, the critical current decreases, non-monotonically, as the Dirac point is approached from the conduction band, and does not increase significantly in the valence band. Focusing first on device 1 (Fig. 3b), we note that the system does not seem to change behaviour at the position of the bottom of the BCB (Vg~−18 V). Below the BCB, Ic continues to decrease until it reaches the Dirac point, near which it saturates to a small but finite value. The finite Ic near the Dirac point may be caused by residual densities in electron-hole puddles due to charged impurity potentials12,18,19,20. Surprisingly, the critical current does not increase in the hole region (Vg<−55 V); this may be related to asymmetric contact resistances21 or to the lack of clear surface states in the valence band (as seen in Fig. 2d). In device 2 (Fig. 3d), Ic becomes zero at large negative gate voltages, even before the Dirac point is reached. In fact, dV/dI exhibits a peak for Vg<−100 V, the height of which increases with lower temperatures. The different behaviour of device 2 at low densities may be due to increased disorder or longer channel length22.
We also examine a further hallmark of the Josephson effect, Fraunhofer behaviour, inside and outside of the topological regime. Figure 4 shows a plot of measured Ic as a function of magnetic field B in device 1 at different gate voltages. The resulting Fraunhofer patterns, the single-slit interference-like dependence of Ic on B in a Josephson junction, demonstrate that the supercurrent through the junction originates from the Josephson effect. Figure 5 shows that while the amplitude of Ic changes with Vg, the period of oscillation of Ic with B does not, for measurements both within and outside the topological regime.
Critical supercurrent Ic versus perpendicular magnetic field B at T=16 mK for device 1 at different gate voltages, showing clear Fraunhofer diffraction patterns. The minima occur at intervals of Ф/Ф0~0.23 n, where n is an integer; however, we plot Ic versus B rather than Ф/Ф0 because the short junction area may be ill-defined due to flux focusing26.
(a) Dependence of critical current Ic on gate voltage Vg for a short channel junction (1:3 length to width ratio) (blue), overlayed with experimental results from device 1 (dashed black). (b) Surface (dashed blue) and bulk (solid blue) density of states (DOS) for the model topological insulator Hamiltonian, mapped to Vg for device 1. The bulk is gapped, with the first states appearing near −38 V (though the majority of bulk subbands appear above −20 V). The peak in the bulk DOS near Vg~ −10 V is not consistent with the monotonicity of the bulk DOS seen in the angle-resolved photoemission spectroscopy data; however, Fig. 4a shows that the bulk DOS does not have a significant role in transport within the junction, and thus the model can capture the salient transport physics. The effect of (c) bulk disorder and (d) surface and bulk disorder on Ic in a long-channel junction (2:1 length to width ratio), for δ-impurity strengths equal to 0, 0.2, 0.5 and 1.0 times the bulk bandgap energy. For this device, bulk states become dominant at approximately −20 V (the DOS is similar to that in 5b, but the gate voltage axis would range from −95 to 45 V due to the disparity in backgate capacitance between devices). In c, the supercurrent only decreases appreciably when the bulk disorder potential is large enough to begin hybridizing bulk and surface bands. Including surface disorder, as in d, causes the supercurrent to degrade immediately, signifying that supercurrent flows primarily through the surface band. Experimental results from device 2 are overlayed on both plots (dashed black).
Discussion
To explain the unique features observed in Ic versus Vg, we compare the experimental data to transport simulations of a model that couples superconducting contacts to a 3D tight-binding Dirac Hamiltonian with an inverted mass gap; this creates a topologically non-trivial Josephson junction that retains the geometry of the samples (Supplementary Notes 1 and 2). Supercurrents and density of states (DOS) profiles are calculated in the non-equilibrium Green function formalism23. Figure 5a shows results for a geometry similar to device 1 overlayed with the measurements; there is excellent correspondence between simulations and experiment. To understand the Ic versus Vg behaviour, we plot the bulk and surface DOS for device 1 in Fig. 5b. Although the model we employ yields residual bulk DOS at Vg<−20 V, brought about by a single bulk subband beginning at Vg=−38 V (set by computational constraints on the Hamiltonian parameters, see Supplementary Note 2), the majority of bulk subbands first appear near Vg=−20 V. As we show below, the bulk is largely inert, and Ic is not dependent on the BCB minimum, so that numerical and experimental results remain compatible. We note that above the Dirac point, Ic closely follows the surface DOS throughout the entire energy range, which explains the non-monotonic behaviour of Ic. The fact that the supercurrent closely matches the surface DOS profile implies that the Josephson current is predominantly carried by the topological surface band, independent of bulk characteristics. Figure 5c shows simulations for a geometry similar to device 2 overlayed with the measurements; again, the simulations match the experiments. The supercurrent has a shape similar to that of device 1, but an insulating regime arises near the Dirac point. This may suggest that for longer junctions the channel becomes insulating above a critical resistance22.
To further understand the surface-dominated supercurrent, we added δ-function impurities of increasing strength (see Supplementary Note 3) to bulk and/or surface regions in the long-channel model (2:1 length to width ratio) to determine the effect of degraded bulk and surface mobility on critical supercurrent. For the model, the bulk and surface are both considered to have mean free paths much longer than the sample size. The effect of disorder localized in the bulk versus disorder in both surface and bulk is shown in Fig. 5c and d, respectively. Decreased bulk mobility (due to disorder) has little effect on Ic until the disorder strength becomes large enough to hybridize the surface band with the bulk, that is, when the impurity strength is comparable to the bandgap energy. Disorder applied equally to bulk and surface states, in contrast, results in a continuous degradation of current as disorder is increased. These simulations strongly suggest that the large majority of supercurrent is carried along the surface of the TI, and that this occurs because of crystal symmetries rather than a discrepancy in bulk and surface mobilities. This is in stark contrast to normal state transport simulations for Bi2Se3, which have shown that when the chemical potential is pushed out of the purely topological regime, current flows primarily through the bulk due to the onset of many additional available states24. We find that the supercurrent only degrades if the surface is encumbered with elastic scattering centres, or if bulk disorder is so large that surface-bulk band hybridization occurs.
Methods
Crystal growth
The crystals of Bi1.33Sb0.67Se3 were grown by using a modified floating zone method in which the melting zone is Se-rich BiSbSe. The materials of high purity 99.9999% Bi, Sb and Se were premelted and loaded into a 10-mm diameter quartz tube. The crystal growth velocity in the quartz tube is 0.5 mm per hour.
ARPES
The ARPES experiments were carried out at the National Synchrotron Light Source, using the VUV undulator beamline U13UB, which is based on a 3-m normal incidence monochromator. The photon energy used in the study was 20.5 eV. The electron analyzer was a Scienta SES-2002, which uses a two-dimensional micro-channel plate as a detector that collects simultaneously a wide energy window and a wide angular window (~14°) of excited photoelectrons. The combined energy resolution was around 8 meV, while the angular resolution was better than ~0.15°, translating into a momentum resolution of~0.005 Å−1 at 20.5 eV photon energy. Samples were mounted on a liquid He cryostat and cleaved in situ and measured at ~15 K in the ultrahigh vacuum chamber with the base pressure 3 × 10−9 Pa.
Device fabrication and measurement
We mechanically exfoliated thin films from bulk (Bi1.33Sb0.67)Se3 crystals on 300 nm SiO2/highly n-doped Si substrates by the ‘scotch tape method’25; films of thickness ~10 nm were found by optical microscope and atomic force microscopy10,11,12. Device 1 has a thickness of 14 nm and dimensions L~0.1 μm and W~1.4 μm, whereas device 2 has a thickness of 12 nm and dimensions L~0.5 μm and W~2.5 μm. Subsequently, electron beam lithography was performed to define a Hall bar and closely spaced junctions in a device. Brief surface cleaning with ion milling and Ti(2.5 nm)/Al(140 nm) deposition were performed at a base pressure~1 × 10−9 Torr with sample substrates cooled to T~77 K. Immediately after lift-off, device 2 was wire-bonded and cooled down in a commercial dilution refrigerator. About 8 nm of F4-TCNQ (Sigma-Aldrich) was deposited on device 1 before wire-bonding and cool-down. We observed 2–3 times higher backgate capacitance (n=CgVg/e, where Cg=20–30 nF cm−2) in device 1 (with chemical dopants), compared with Cg~11 nF cm−2 in device 2 (with no chemical dopants). Similar values of enhanced backgate capacitance at low temperature in thin Bi2Se3 devices doped with polymer electrolyte were reported previously,12 however the origin is not well understood.
Additional Information
How to cite this article: Cho, S. et al. Symmetry protected Josephson supercurrents in three-dimensional topological insulators. Nat. Commun. 4:1689 doi: 10.1038/ncomms2701 (2013).
References
Hasan, M. Z. & Kane, C. L. . Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Fu, L. & Kane, C. L. . Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Qi, X. -L. & Zhang, S. -C. . Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Nilsson, J., Akhmerov, A. R. & Beenakker, C. W. . Splitting of a Cooper pair by a pair of Majorana bound states. Phys. Rev. Lett. 101, 120403 (2008).
Tanaka, Y., Yokoyama, T. & Nagaosa, N. . Manipulation of the Majorana fermion, Andreev reflection, and Josephson current on topological insulators. Phys. Rev. Lett. 103, 107002 (2009).
Veldhorst, M. et al. Josephson supercurrent through a topological insulator surface state. Nat. Mater. 11, 417–421 (2012).
Zhang, D. M. et al. Superconducting proximity effect and possible evidence for Pearl vortices in a candidate topological insulator. Phys. Rev. B 84, 165120 (2011).
Sacépé, B. et al. Gate-tuned normal and superconducting transport at the surface of a topological insulator. Nat. Commun. 2, 575 (2011).
Williams, J. R. et al. Unconventional Josephson effect in hybrid superconductor-topological insulator devices. Phys. Rev. Lett. 109, 056803 (2012).
Checkelsky, J. G., Hor, Y. S., Cava, R. J. & Ong, N. P. . Bulk band gap and surface state conduction observed in voltage-tuned crystals of the topological insulator Bi2Se3 . Phys. Rev. Lett. 106, 196801 (2011).
Cho, S., Butch, N. P., Paglione, J. & Fuhrer, M. S. . Insulating behavior in ultrathin bismuth selenide field effect transistors. Nano Lett. 11, 1925–1927 (2011).
Kim, D. et al. Surface conduction of topological Dirac electrons in bulk insulating Bi2Se3 . Nat. Phys. 8, 459–463 (2012).
Kong, D. et al. Ambipolar field effect in the ternary topological insulator (BixSb1-x)2Te3 by composition tuning. Nat. Nanotech. 6, 705–709 (2011).
Hong, S. S., Cha, J. J., Kong, D. & Cui, Y. . Ultra-low carrier concentration and surface-dominant transport in antimony-doped Bi2Se3 topological insulator nanoribbons. Nat. Commun. 3, 757 (2012).
Hsieh, D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101–1105 (2009).
Kuroda, K. et al. Hexagonally deformed Fermi surface of the 3D topological insulator Bi2Se3 . Phys. Rev. Lett. 105, 076802 (2010).
Adam, S., Hwang, E. H. & Das Sarma, S. . Two-dimensional transport and screening in topological insulator surface states. Phys. Rev. B 85, 235413 (2012).
Adam, S., Hwang, E. H., Galitski, V. M. & Das Sarma, S. . A self-consistent theory for graphene transport. Proc. Natl Acad. Sci. USA 104, 18392–18397 (2007).
Beidenkopf, H. et al. Spatial fluctuations of helical Dirac fermions on the surface of topological insulators. Nat. Phys. 7, 939–943 (2011).
Martin, J. et al. Observation of electron-hole puddles in graphene using a scanning single-electron transistor. Nat. Phys. 4, 144–148 (2008).
Cho, S. & Fuhrer, M. . Massless and massive particle-in-a-box states in single- and bi-layer graphene. Nano Res. 4, 385–392 (2011).
Abrahams, E., Kravchenko, S. V. & Sarachik, M. P. . Metallic behavior and related phenomena in two dimensions. Rev. Mod. Phys. 73, 251–266 (2001).
Datta, S. . Quantum transport : atom to transistor Cambridge University Press (2005).
Dellabetta, B., Hughes, T. L., Gilbert, M. J. & Lev, B. L. . Imaging topologically protected transport with quantum degenerate gases. Phys. Rev. B 85, 205442 (2012).
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl Acad. Sci. USA 102, 10451–10453 (2005).
Grimaldi, G., Gambardella, U. & Pace, S. . Inhomogeneous magnetic flux focusing in superconducting Josephson networks. Phys. Rev. B 59, 13608–13611 (1999).
Acknowledgements
N.M., S.C. and M.J.G. acknowledge support from the ONR under grant N0014-11-1-0728. M.J.G. and B.D. acknowledge support from the AFOSR, under grant FA9550-10-1-0459. Device fabrication was carried out in the Materials Research Laboratory Central Facilities (partially supported by the DOE, under DE-FG02-07ER46453 and DE-FG02-07ER46471). The work at Brookhaven National Laboratory was supported by the US Department of Energy, Office of Basic Energy Sciences, under contract DE-AC02-98CH10886. S.C. acknowledges useful discussions with W.K. Park, J. Ku, D. Kim, S. Adam and M. Fuhrer.
Author information
Authors and Affiliations
Contributions
S.C. fabricated devices and carried out transport experiments. A.Y., J.S., Z.J.X. and G.G. grew the (BixSb2−x)Se3 crystal. T.V. performed ARPES measurements. S.C., B.D., M.J.G. and N.M. analysed the data and wrote the main paper. B.D. and M.J.G. wrote the Supplementary Information.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Notes 1-3 and Supplementary References (PDF 109 kb)
Rights and permissions
About this article
Cite this article
Cho, S., Dellabetta, B., Yang, A. et al. Symmetry protected Josephson supercurrents in three-dimensional topological insulators. Nat Commun 4, 1689 (2013). https://doi.org/10.1038/ncomms2701
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2701
This article is cited by
-
Dual topological states in the layered titanium-based oxypnictide superconductor BaTi2Sb2O
npj Quantum Materials (2022)
-
Josephson current mediated by ballistic topological states in Bi2Te2.3Se0.7 single nanocrystals
Communications Materials (2020)
-
Highly skewed current–phase relation in superconductor–topological insulator–superconductor Josephson junctions
npj Quantum Materials (2020)
-
Finite momentum Cooper pairing in three-dimensional topological insulator Josephson junctions
Nature Communications (2018)
-
Induced unconventional superconductivity on the surface states of Bi2Te3 topological insulator
Nature Communications (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.